节流式燃/氧分离发动机准一维内弹道数值研究

王革，王志邦，王富祺，关奔，*，王立民，宁浩然

1.哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001

2.国防科技大学 空天科学学院，长沙 410073

3.内蒙动力机械研究所，呼和浩特 010011

4.哈尔滨商业大学 能源与建筑工程学院，哈尔滨 150028

固体火箭发动机（Solid Rocket Motor，SRM）具有结构简单、响应速度快、可靠性高、成本低等优点，被广泛应用于各种航天运输系统和战略导弹中。高能量和高安全性一直是固体火箭发动机不断追求的两大特性。美国洛斯阿拉莫斯国家实验室（Los Alamos National Laboratory，LANL）的Tappan［1-2］和Lichthardt［3］等提出了燃料-氧化剂分离系统（Segregated Fuel-Oxidizer System，SFOS）的 概念，也可称为燃/氧分离发动机。燃/氧分离发动机将固体燃料和固体氧化剂药柱以串联的方式分段排列。固体燃料和固体氧化剂对冲击相对不敏感，大大降低了火箭发生意外爆炸的几率。LANL 提出的燃/氧分离发动机为固体火箭发动机提供了能够同时实现高能量和高安全性的新发展方向。

最近，Zou等［4］对组合式固体火箭发动机的内弹道性能进行了数值研究。他们在LANL 的燃/氧分离发动机基础上安装流量调节阀将组合式固体火箭发动机燃烧室分为富氧燃烧室和富燃燃烧室。其数值结果表明，改变流量调节阀的喉部面积可以改变燃气质量流量进而改变发动机推力。因此，组合式固体火箭发动机不仅具有安全、可靠等优点，也具有性能主动调控的特征，具备在战略导弹中应用的潜质，使其具备高机动突防的能力。然而，他们的数值模型并未包含整个发动机的两个燃烧室，缺少流量调节阀前的燃烧室。另外，采用质量流量入口边界条件无法计算燃烧室压力与燃气质量流量之间的耦合响应关系，还有进一步改进的空间。

燃/氧分离发动机的概念较新颖，相关研究报道较少，但在过去的几十年中，许多预测固体火箭发动机以及超燃冲压发动机性能的一维数值方法相继涌现，这为本文的数值模型构建打下了坚实基础。在以往的研究中，一维内弹道模型已经被广泛应用于预测固体火箭发动机准稳态和瞬态工作状态下的内弹道参数［5-12］、研究发动机的不稳定燃烧［13-14］以及模拟混合火箭发动机的燃烧过程［15-16］，这些一维模型极大地帮助了研究人员快速地对火箭发动机性能进行研究和分析。但大多数固体火箭发动机一维内弹道数值模型仅适用于简单结构的发动机，较少综合考虑截面面积变化、燃面退移、燃气注入及化学反应等因素对发动机流场的影响。因此，需要借鉴超燃冲压发动机一维数值方法进一步完善和补充数值模型，以建立能够准确预测燃/氧分离发动机工作过程中内流场参数分布以及性能变化的准一维内弹道模型。以往一维模拟的数值方法主要包括两类：采用空间推进求解常微分方程组的稳态求解方法［17］和采用时间步进求解偏微分方程组的非稳态方法［18］。稳态求解方法［19-23］精度不高，在求解跨声速反应流时存在奇异性，而非稳态方法则能够更好地求解燃烧流动耦合关系。Bussing和Murman［18］率先提出了基于偏微分方程的超燃冲压发动机一维模型，后续学者们［24-27］对该模型不断改进和完善，充分考虑了面积变化、壁面摩擦、质量添加、化学反应、壁面热损失以及两相流动等因素的影响。为本文能够更加准确地模拟燃/氧分离发动机燃烧室内两种燃气的流动、掺混及燃烧现象奠定了坚实的数值基础。

本文结合LANL 的燃/氧分离发动机以及Zou等［4］提出的组合式固体火箭发动机，研究了节流式燃/氧分离发动机的推力调节特性。该发动机保持了前端富燃燃烧室和后端富氧燃烧室（与LANL的燃/氧分离发动机相同）的构型，在两燃烧室中间安装流量调节阀以对富燃燃气质量流量进行调控。本研究的目的是针对整个发动机结构，提供节流式燃/氧分离发动机内弹道的快速预测，为节流式燃/氧分离发动机构型建立非定常准一维内弹道数值模型。数值模型考虑燃气注入、壁面摩擦和推进剂燃面退移等因素，采用有限速率化学反应模型结合简化的反应机理计算推进剂燃烧反应。利用该数值模型，首先对LANL 的燃/氧分离发动机的内弹道进行仿真计算，验证数值模型的可靠性。然后通过考虑流量调节阀的作动，研究节流式燃/氧分离发动机调节阀的静态工作过程（流量调节阀喉部半径保持不变）和动态工作过程（流量调节阀喉部半径动态变化）对发动机推力性能的影响，对节流式燃/氧分离发动机的推力调节能力提出理论预测，对推力调控影响因素进行分析。最后，根据分析结果提出了喷管流量可调的改进型节流式燃/氧分离发动机方案。

1 数值模型和求解方法

1.1 控制方程

节流式燃/氧分离发动机内弹道可以用可压缩、多组分、化学非平衡流的非定常准一维控制方程很好地描述：

式中：U为守恒量；F为对流通量；Fv为黏性通量；S为用来描述燃气注入、壁面摩擦和化学反应的源项。

式中：ρ、p和E 分别为混合气体密度、压力以及单位质量的总能量；u 为混合物的速度；Yi为第i 种组分的质量分数；NS为组分总数；A 为发动机随时间变化的燃烧室横截面积；Jx，i、σx和qx分别为组分i 的质量扩散通量、黏性应力和热扩散量为第i 种组分的质量添加项为组分i 的质量分数变化量；f 为壁面摩擦力系数；Cw为湿周长；usx为沿x 方向燃料的喷射分速度（富燃燃气和富氧燃气为垂直注入，所以此项为0）；Hsi为添加燃气的滞止焓和化学反应释放热量之和。

利用理想气体状态方程将压力、燃气组分、温度和密度联系起来：

式中：Mωi为组分i 的摩尔分子量；T 为混合物温度；Ru为通用气体常数。

1.2 源项确定

对于源项算子，必须考虑3 个因素，即燃气的注入、推进剂药柱的退移、燃气和腔壁的流动摩擦，下面介绍各因素的模型。

富燃燃气的注入采用平均质量添加模型：

式中：a*为燃速系数；pav为每个推进剂段的平均压力；n 为压力指数。表1［29-30］列出了不同推进剂的a*和n值。

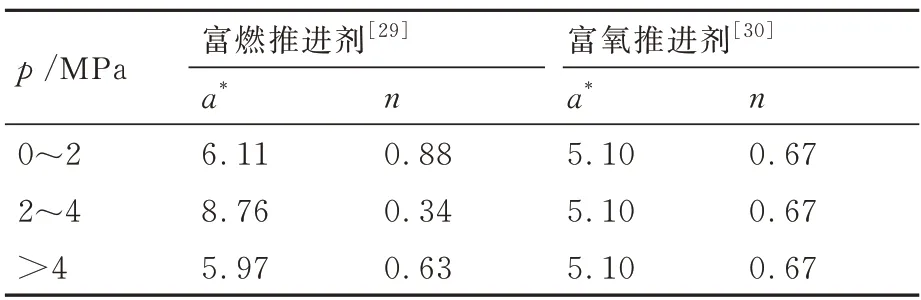
表1 富燃推进剂和富氧推进剂燃速系数a*和压力指数n 的数值Table 1 Values of burning rate a* coefficients and pressure index n of fuel-rich and oxygen-rich propellants

燃烧室中气流的壁面摩擦系数f为［31］

式中：Re和Ma 分别为局部雷诺数和马赫数；γ 为混合燃气比热比。

1.3 数值求解方法

控制方程采用有限差分方法进行离散。利用算子分裂方法，将控制方程分解为两个非刚性的流动算子（无黏算子和黏性算子）和一个刚性源项算子，使它们可以根据数值性质分别求解。

1.3.1 流动算子求解

对于无黏算子，使用AUSM+-up［32］计算无黏通量，并采用MUSCL 格式计算单元界面的变量［33］。双通量模型［34］和人工黏性方法［35］用于消减界面上由于多组分物质比热不同而导致的参数振荡。使用三阶TVD Runge-Kutta 格式进行时间积分［36］。对于黏性算子，采用二阶中心差分格式计算黏性项，采用二阶显式 Runge-Kutta-Chebyshev 格式［37］对其时间步长进行积分。本文数值方法的详细信息可参考文献［38］。

1.3.2 化学反应求解及反应机理

本文中的化学反应使用每种气体组分的密度和能量方程来表示：

式中：ρi为第i 种组分的密度为组分i 的滞止焓；E 为单位质量的总能量。

能量是温度的函数：

式中：Ri为组分i 的气体常数为组分i 在温 度T 下的显焓。

将式（12）代入式（11），得到温度方程为

式中：cpi为组分i 的定压比热；hi为组分i 的静焓。

各气体组分的温度可以用二阶梯形公式［39］求解，通过求解温度，可以得到能量和比热比。

为简化燃烧反应机理，假设富氧推进剂仅含有高氯酸铵（AP）；富燃推进剂含有质量分数为60%的三氨基胍硝酸盐（TAGN）和质量分数为40%的3，3-二叠氮甲基氧丁环-四氢呋喃共聚醚（PBT）。AP、TAGN 以及PBT 热分解的气相组分可参考文献［40］。

富燃推进剂气相组分中的主要燃料为CO、H2以及CH4；富氧推进剂气相组分中的主要氧化剂为O2。忽略其他次要组分，确定富燃燃气和富氧燃气的三步总包反应机理，如表2 所示。根据该反应机理，可以计算出化学当量比（富燃燃气与富氧燃气完全燃烧时的质量流量之比）为0.374。化学反应计算采用基于Arrhenius 公式的有限速率化学反应模型：

式中：Ak为指前因子；βk为温度因子；Eak为化学反应的活化能；Ru为通用气体常数。

1.4 发动机性能计算

发动机推力F和比冲Isp的计算方式为

1.5 数值验证

1.5.1 超燃冲压发动机内弹道验证

本文中的非定常准一维内弹道模型可以通过模拟由Billig和Grenleski［41］以及O’Brien等［28］进行的氢燃料超燃冲压发动机实验进行验证。如图1 所示，实验装置为轴对称壁面喷射超燃冲压发动机。其燃烧室由一个恒定面积为0.003 8 m2、长度为0.28 m 的圆柱体组成，随后是一个长度为0.61 m、面积比为2 的锥形膨胀段。喷油器位于x=0 位置，左边界采用质量流量入口边界条件来模拟空气的注入，出口边界根据内流场外推得到。按照O’Brien等［28］提供的初始设置，进入燃烧室的条件为U=1 849 m/s；p=52 000 N/m2；T=872 K；Tw=500 K；γ=1.346；Ma=3.19。

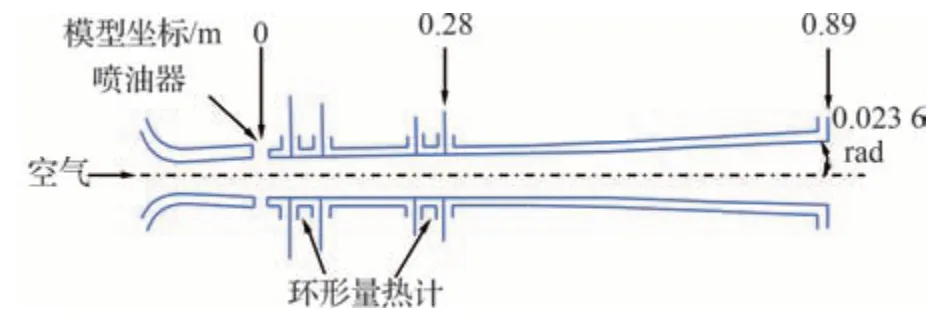
图1 Billig和Grenleski 实验［41］中的超燃冲压发动机燃烧室结构模型Fig.1 Structural model of scramjet combustion chamber in Billig &Grenleski［41］ experiment

将利用本文数值方法得到的燃烧室流动结果 与Billig和Grenleski［41］的实验 结果以及O’Brien等［28］的数值结果进行比较。结果表明，三者在沿燃烧室壁面的无量纲压力分布（pw/p0，壁面压力与总压的比值，如表3 所示）一致性较好。与实验数据相比，其平均误差在15%以内。

表3 Billig和Grenleski 的实验结果、O’Brien 等的数值结果与本文数值结果的比较Table 3 Comparison of experimental results of Billig &Grenleski，numerical results of O’Brien et al.，and numerical results of present study

1.5.2 燃/氧分离发动机仿真验证

将LANL 的燃/氧分离发动机的几何构型进行简化，如图2 所示。在燃烧室内，装填两个分离的推进剂药柱，前端药柱为富燃推进剂，后端药柱为富氧推进剂。在后端药柱和喷管收敛段之间，存在一混燃室。根据Tappan等［2］的实验，其燃/氧分离发动机的推力约为111.25 N，比冲为2 069.76 m/s，富燃燃烧室的工作压力为4.38 MPa，富氧燃烧室的工作压力为4.17 MPa。可推算得到流出发动机的质量流量为0.053 7 kg/s、喷管喉部半径为2.43 mm、喷管出口半径为5.5 mm。假设推进剂为恒面燃烧，燃面退移过程中药柱肉厚及燃面位置发生变化但燃面面积保持不变，因此拟定两种推进剂装药均为星型药柱。根据式（8）计算两种推进剂药柱的燃面面积Ab（假设富燃与富氧燃气注入速率相等==0.026 85 kg/s），计算得到富燃推进剂药柱的Ab为934.4 mm2，富氧推进剂药柱的Ab为1 243.4 mm2。

在数值模拟过程中，燃烧室内部初始工作压力和温度分别为1.0 MPa和600 K，喷管扩张段初始环境压力和温度分别给定为101 325 Pa和293 K。富燃燃气和富氧燃气的质量流量比为1∶1，即==0.026 85 kg/s。发动机头部为固壁边界条件，喷管出口采用外推法直接得到出口边界条件。

富燃燃烧室平均压力pf、富氧燃烧室平均压力po、发动机推力F和比冲Isp变化情况分别如图3 所示。在0.03 s内，富燃燃烧室和富氧燃烧室的压力分别达到4.42 MPa和4.38 MPa，之后分别保持相对稳定，发动机进入稳定工作状态（本文将该状态定义为在0.01 s 的时间间隔内发动机内流场参数的相对变化<0.1% 的状态），如图3（a）所示。发动机推力F和比冲Isp变化具有相似性。在发动机初始工作瞬间产生突跃后，推力和比冲经历一个短暂振荡阶段，然后达到稳定工作状态，如图3（b）和图3（c）所示。

图3 燃烧室压力、推力和比冲的变化过程Fig.3 Histories of combustion chamber pressure，thrust and specific impulse

表4 将当前的数值结果pf、po、F和Isp与Tappan 等的实验数据［2］进行对比，结果发现数值结果与实验数据的误差不到10%，由此可验证本文准一维数值模型的可靠性。

表4 Tappan 等的实验数据与现有模型结果对比Table 4 Comparison of Tappan et al.’s experimental data and present model results

2 节流式燃/氧分离发动机

2.1 物理模型及边界条件

节流式燃/氧分离发动机的构型如图4 所示，坐标原点O（x=0）位于发动机头部轴线端点处，沿发动机轴向为x 方向。对于流量调节阀部分，使用sin x和cos x 函数来描述两个燃烧室之间连续过渡的横截面积。当调节阀喉部半径R 发生改变时，富燃燃气的质量流量发生变化，两个燃烧室的压力和推进剂燃烧速率也相应改变。从而使得节流式燃/氧分离发动机内弹道性能可以实现主动调控。

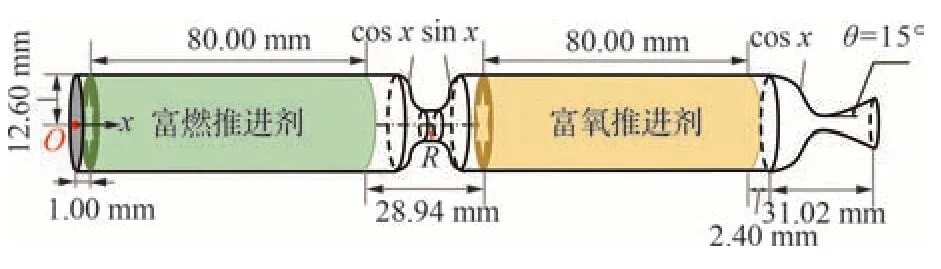
图4 节流式燃/氧分离发动机几何构型示意图Fig.4 Schematic diagram of throttling SFOS geometric configuration

发动机燃烧室初始压力和温度分别为0.5 MPa和600 K，喷管扩张段初始环境压力和温度分别为101 325 Pa和293 K。发动机头部为固壁边界条件，喷管出口边界根据内流场外推得到。从两个燃烧室的推进剂药柱区域分别向燃烧室内注入两种燃气，其中富燃燃气注入温度为1 200 K，富氧燃气注入温度为1 680 K，两种燃气的质量流量均由式（8）算得。

2.2 网格与时间步长无关性验证

采用200、300、500、800和1 200 个网格节点求解节流式燃/氧分离发动机内部沿轴向的压力和速度分布情况，进行网格无关性验证，计算网格为均匀网格，5 种网格对应的网格大小分别为1.12、0.75、0.45、0.28 以及0.19 mm，验证结果如图5 所示。可以看出，对于每个参数，其相邻分布曲线的差异随着网格节点数量的增加而变小。当网格节点数达到800 或更多时，该准一维内弹道模型的模拟结果受网格数量影响较小。

图5 网格无关性验证结果Fig.5 Results of grid independence test

同时，分析时间步长对沿轴向压力和速度分布情况的影响，计算结果如图6 所示。当时间步长减小到1.0×10-7s 或更小时，计算结果受时间步长影响较小。综合考虑计算结果和效率，确定在后续研究中计算域网格节点数为800，网格大小为0.28 mm，时间步长设置为1.0×10-7s。

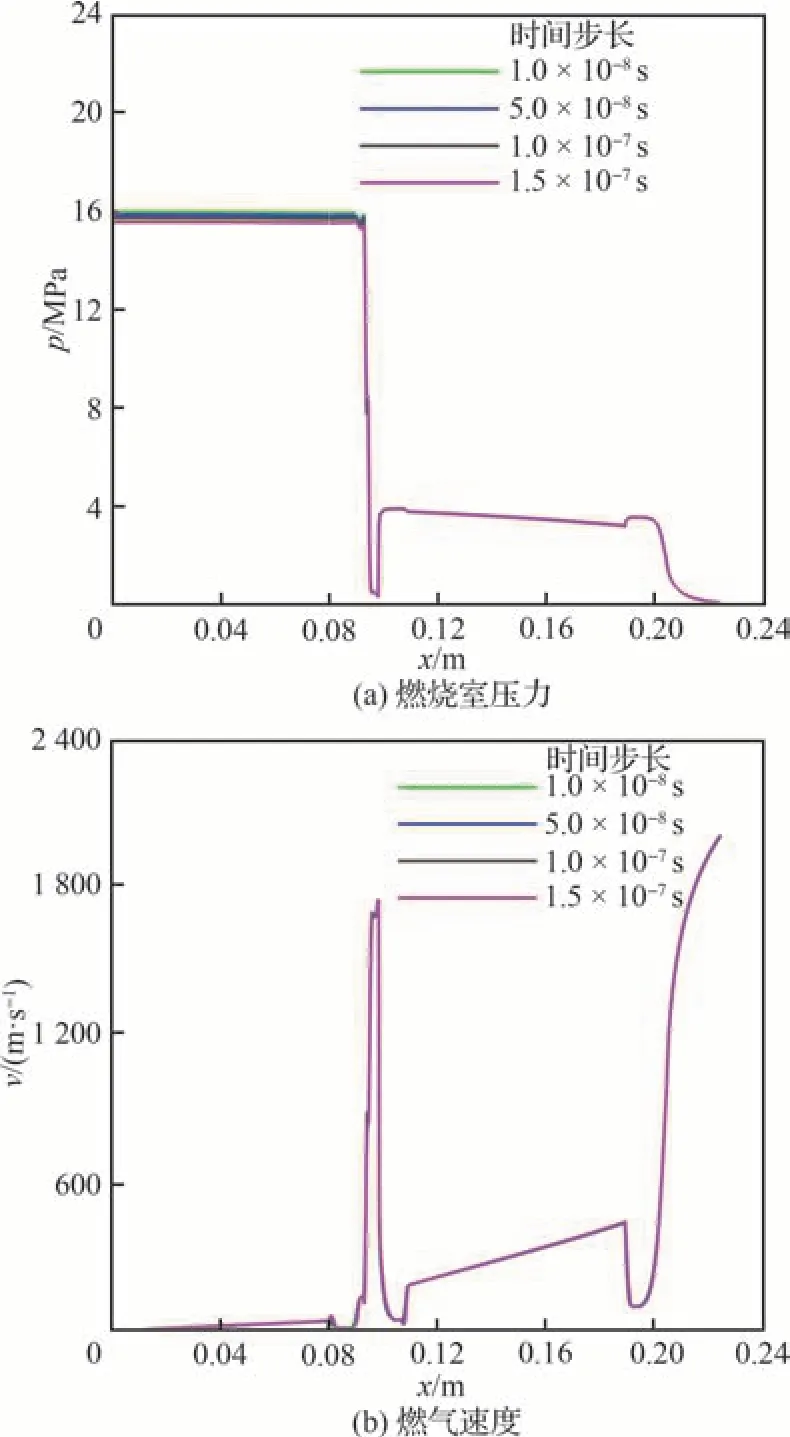
图6 时间步长无关性验证结果Fig.6 Results of time step independence test

2.3 调节阀保持静态时节流式燃/氧分离发动机工作过程

计算调节阀静态工作时不同喉部半径下（R=2.89、2.84、1.90、1.65 mm）节流式燃/氧分离发动机稳定工作状态下的流动特性。4 种不同调节阀开度的工况分别被命名为R-2.89、R-2.84、R-1.90和R-1.65。R-2.89 状态为发动机流量调节前的初始状态，图7 以R-2.89 状态为参考工况比较了4 种工况调节阀静态工作运行状态下的内流场压力、温度、速度和马赫数，图7 中所展示的流场参数分布时刻分别对应于发动机4 种工况下流场参数保持相对稳定的工作状态。R-2.84 工况与参考工况下的参数分布差异很小。但随着调节阀的喉部半径减小，富燃燃烧室的压力逐渐升高。富燃燃烧室内的高压增大了推进剂的燃烧速率，增加了流过调节阀的燃气质量流量，从而提高了下游富氧燃烧室的压力。同时，富燃燃烧室压力与富氧燃烧室压力的比值增大使得调节阀处的马赫数增大。R-2.84 工况下调节阀出口马赫数为1，如图7（d）所示，调节阀处燃气流动为临界状态。R-2.89 工况调节阀处燃气流动为亚临界状态，整个发动机内部流动为亚声速；而R-1.90和R-1.65 工况下调节阀处气体流动为超临界状态，此时调节阀后有激波形成。

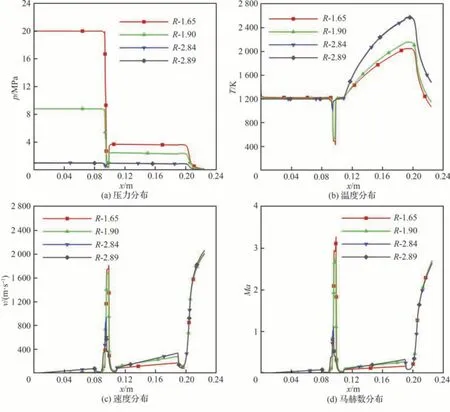
图7 调节阀保持静态时不同喉部半径下节流式燃/氧分离发动机的流场参数Fig.7 Flow parameters of throttling SFOS with different valve opening radii while valve is steady

各主要产物组分在发动机轴线方向上的质量分数分布如图8 所示。在富燃燃烧室中，富燃燃气（H2和CH4，如图8（a）和图8（b）所示）的质量分数保持不变。富氧推进剂AP 的热分解产物主要包括H2O、O2和HCl 等组分［40］，富氧推进剂燃烧使富氧燃烧室前端部分的HCl 的质量分数迅速上升（图8（c））。当富燃燃气进入富氧燃烧室，与富氧燃气进一步掺混燃烧，富燃燃气H2和CH4的质量分数明显减小。

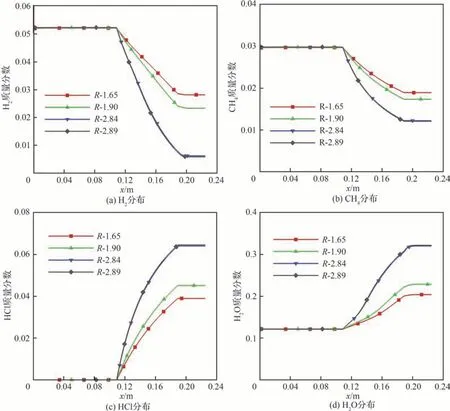
图8 调节阀保持静态时不同喉部半径下节流式燃/氧分离发动机的组分分布Fig.8 Composition distributions of throttling SFOS with different valve opening radii while valve is steady

流量调节阀喉部半径的减小使得发动机富氧燃烧室与混燃室内的温度以及温度的爬升速率降低，如图7（b）所示。富燃燃气H2和CH4的消耗率以及消耗速率也相应降低，如图8（a）和图8（b）所示，由此可知调节阀喉部半径减小导致燃烧效率降低。这是因为较小的喉部半径使得富燃燃气的质量流量与富氧燃气的质量流量之比与化学反应的化学当量比偏离得更远，从而降低了燃烧效率。最终产物H2O（图8（d））的质量分数是发动机内燃烧效率最直接的指标。当调节阀喉部半径为1.65 mm时，最终产物质量分数显著低于调节阀喉部半径较大的工况。

节流式燃/氧分离发动机在4 种调节阀静态工作时不同喉部半径工况下的推力和比冲列于表5中。数据表明，调节阀喉部半径越小，两种燃气的质量流量越大，发动机推力越大。调节阀喉部半径由2.89 mm 减小到2.84、1.90 以及1.65时，相应的发动机推力由105.09 N 分别增加至107.35、285.29 以及432.18 N，这表明调节阀喉部半径确实对节流式燃/氧分离发动机的性能调控起到决定性作用。当发动机需要大推力时，调节阀喉部半径应减小。

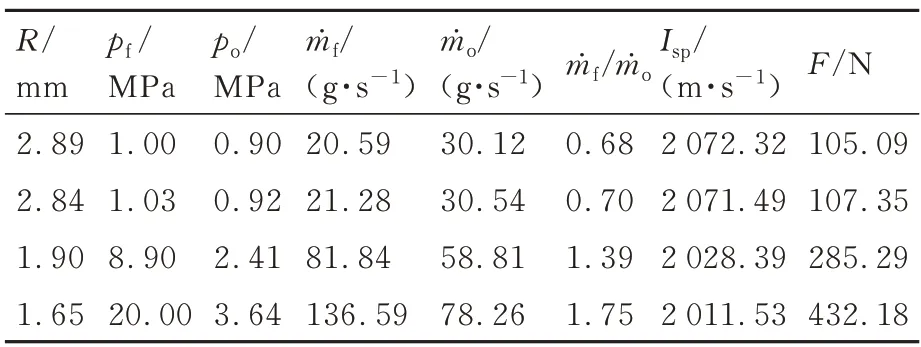
表5 不同调节阀喉部半径下节流式燃/氧分离发动机的性能参数Table 5 Performance parameters of throttling SFOS with different throttle valve throat radii

表6 不同/At 下发动机调节前后的内弹道参数（N=4.00）Table 6 Internal ballistic parameters before and after motor performance regulation with different/At（N=4.00）

表6 不同/At 下发动机调节前后的内弹道参数（N=4.00）Table 6 Internal ballistic parameters before and after motor performance regulation with different/At（N=4.00）

2.4 调节阀动态调节时节流式燃/氧分离发动机工作过程

已知节流式燃/氧分离发动机依靠流量调节阀的作动能够实现发动机推力性能的主动调控，现将流量调节阀喉部半径从2.89 mm 连续地减小到1.65 mm，以检验节流式燃/氧分离发动机调节阀动态工作过程。图9 展示了节流式燃/氧分离发动机流量调节阀3 次启动（如图9 中垂直虚线所示）和停止过程中燃烧室压力和发动机推力仿真计算结果的变化过程。调节阀作动速度为1.0 m/s。发动机工作初始条件及边界条件与2.1 节中的设置一致。

图9 节流式燃/氧分离发动机动态调节时的燃烧室压力和推力仿真计算结果变化曲线Fig.9 Histories of combustion chamber pressure and thrust simulation results of throttling SFOS dynamic operation

从图9 可以看出，发动机点火后，富燃燃烧室和富氧燃烧室的压力以及发动机的推力在点火后0.2 s 内进入稳定状态。流量调节阀在0.200 00 s 时第一次启动，在0.200 05 s 时第一次停止作动，在此期间调节阀喉部半径从2.89 mm 减小到2.84 mm。调节阀第一次作动结束后，发动机逐渐进入稳定工作状态，第一次调节前后燃烧室压力和发动机推力变化不大。结合图7 调节阀静态工作时不同喉部半径下节流式燃/氧分离发动机流场参数分析可知，在此过程中调节阀处燃气流动由亚临界状态转变为临界状态。流量调节阀在0.360 05 s 时第二次启动，在0.360 99 s 时停止作动。在此期间，调节阀喉部半径从2.84 mm 减小到1.90 mm，富氧燃烧室压力和推力出现明显的负调现象。此后，发动机燃烧室压力和推力显著增加，且富燃燃烧室与富氧燃烧室压力之差不断增大，发动机逐渐重新进入稳定工作状态。流量调节阀在0.520 99 s 时第三次启动，在0.521 24 s 时停止作动，调节阀喉部半径从1.90 mm 减小到1.65 mm，在此期间，发动机内流场流动现象与调节阀第二次启动停止过程相比，出现更为明显的负调现象。该动态工作过程也表明，仅当调节阀处燃气流动处于临界或超临界状态时，调节阀的作动才会使得富氧燃烧室压力和推力出现负调现象。

为了检验流量调节阀作动速度对发动机调节过程中负调现象的影响，现针对流量调节阀第二次启 动及停 止过程，计 算0.2、1.0、5.0和25.0 m/s 这4 种不同调节阀作动速度下（分别记为V-0.2、V-1.0、V-5.0和V-25.0）节流式燃/氧分离发动机工作过程性能参数变化情况，如图10 所示。可以看到，流量调节阀作动未对富燃燃烧室压力产生显著影响，而富氧燃烧室压力和发动机推力则出现明显负调现象，4 种不同作动速度下（0.2、1.0、5.0和25.0 m/s）富氧燃烧室压力的负调量分别为调节前稳定值的5.68%、19.01%、19.72%和19.79%；发动机推力的负调量分别为调节前稳定值的5.74%、19.23%、20.05%和20.18%。负调持续时间分别为4.50、3.30、3.00和2.90 ms。在一定的调节阀作动速度范围内（0.2～5.0 m/s），作动速度越大，发动机富氧燃烧室压力及发动机推力的负调现象越明显，而发动机燃烧室压力及推力响应速度越快，燃烧室压力及推力的爬升速度越快，结束负调现象的时间越早。但继续增大调节阀作动速度（5.0～25.0 m/s）发现，发动机富氧燃烧室压力、发动机推力的负调量及响应时间均无明显变化。因此，需要选择合适的调节阀作动速度以使发动机性能参数的负调量及响应时间均能够满足工作要求。

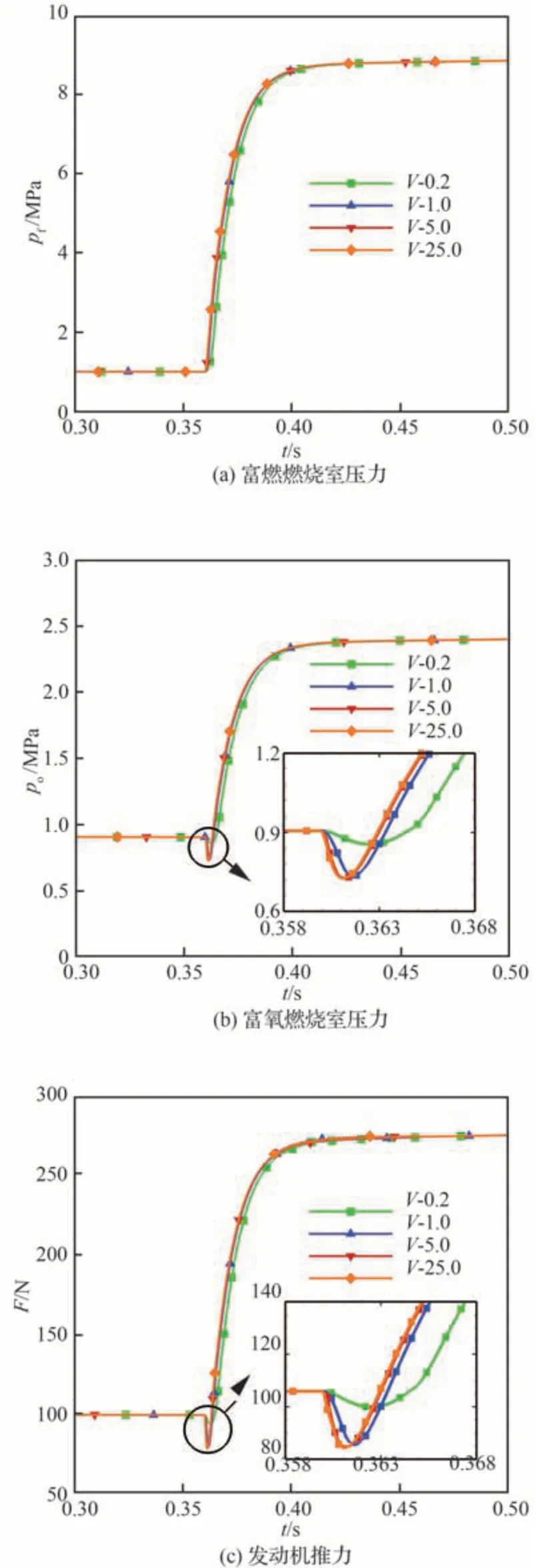
图10 调节阀第二次启动及停止过程中富燃燃烧室压力、富氧燃烧室压力和推力曲线Fig.10 Histories of fuel-rich combustion chamber pressure，oxygen-rich combustion chamber pressure，and thrust during second regulating start and stop of throttle valve

由发动机工作过程可知，调节阀喉部半径的减小使得两个燃烧室的压力上升，从而增大了燃气质量流量，最终使推力显著增加。随着调节阀喉部半径的减小，富燃燃烧室压力上升幅度越来越显著，其对调节阀作动的响应也越来越敏感。在第二次流量调节过程中，调节阀喉部半径减小量为0.94 mm，减小幅度为33.10%，富燃燃烧室压力上升7.87 MPa；第三次流量调节过程中，调节阀喉部半径减小量为0.25 mm，减小幅度为13.16%，富燃燃烧室压力却上升11.12 MPa。另外，由式（8）和式（16）可知，受富燃燃烧室压力影响，调节阀喉部半径的减小使得发动机富燃燃气质量流量以及发动机推力等性能参数对调节阀作动的响应也会越来越敏感。

3 次流量调节使得富燃燃烧室内的压力由1.00 MPa 提高到20.00 MPa，富氧燃烧室内的压力由0.90 MPa 提高到3.64 MPa，发动机推力也由105.09 N 提高到432.18 N，即推力提升至原有推力的411.25%。发动机经过调节阀动态工作过程和调节阀静态工作过程后，其性能参数一致，这说明节流式燃/氧分离发动机具有良好的稳定性。

3 性能调控机理

3.1 性能调控机理关系式建立

2.3 节中的表5 还传达出一个重要信息，即发动机推力的显著提升很大程度上取决于调节阀喉部半径减小所导致的富燃燃气和富氧燃气质量流量增加。因此，燃气质量流量的调节是节流式燃/氧分离发动机推力调节的主导因素，用符号“-”表示推力调节后的参数。

为了简化节流式燃/氧分离发动机推力调节问题的复杂程度，做出如下假设：①忽略静推力的贡献以及比冲的变化，认为质量流量调节比与发动机推力调节比等效；②不考虑流量调节阀及喷管等结构的烧蚀情况；③流量调节过程中，发动机流量调节阀处燃气流动为临界或超临界状态；④推进剂燃速满足维耶里燃速公式，即=a*

用N 表示推力调节后与调节前总燃气质量流量之比，即

调节前后富燃燃气的质量流量之比可以用富燃推进剂燃速与燃面面积的乘积来表示：

式中：nf为富燃推进剂的压力指数。同样，调节前后富氧燃气的质量流量之比可以写成

式中：no为富氧推进剂的压力指数。调节前后富燃燃气质量流量之比用xf表示

调节前的富燃燃烧室压力和富氧燃烧室压力满足

调节后富氧燃烧室与富燃燃烧室的压力比用y 表示

调节前喷管喉部面积At与调节后喷管喉部面积满足

根据上述节流式燃/氧分离发动机性能调节前后各燃烧室燃气质量流量的关系、各燃烧室压力的关系以及发动机结构尺寸的关系列出方程组并求解，可得

通过上述推导可知，节流式燃/氧分离发动机的工作状态（包括推力调节前后富燃燃烧室和富氧燃烧室的压力之比和质量流量之比）可由式（25）～式（28）描述。

3.2 性能调控影响因素分析

节流式燃/氧分离发动机在推力调控过程中最显著的特征是燃烧室压力的变化，不同推力调节比对应不同的燃烧室压力调节比，而燃烧室压力的大小直接关系到发动机能否在壳体最大承压能力下安全稳定工作。因此，选择调节后与调节前富燃燃烧室压力之比作为评判节流式燃/氧分离发动机性能调控能力的参数。富燃燃烧室压力参数的变化情况主要有以下影响因素：①质量流量调节比N；② 初始富燃燃气与富氧燃气质量流量比；③调节后推进剂压力指数和

结合上述影响因素对节流式燃/氧分离发动机性能调控能力进行分析，如图11 所示。可看出随着质量流量调节比N 以及初始富燃燃气与富氧燃气质量流量比的变化，分别绘制出3 个富燃 推进剂 压力指 数（0.50、0.56和0.63，见图11（a））以及富氧推进剂压力指数（0.40、0.53和0.67，见图11（b））下发动机调节后与调节前富燃燃烧室压力之比/pf。图11 中F-O 0.50-0.67 表示富燃推进剂压力指数为0.50、富氧推进剂压力指数为0.67。由式（25）和式（26）可知，富氧推进剂压力指数对发动机性能调控能力的影响小于富燃推进剂压力指数，因此，富氧推进剂压力指数的变化范围更大。假设发动机壳体最大承压能力为20 MPa，发动机富燃燃烧室初始压力为1.00 MPa（见表5），因此认为调节后与调节前富燃燃烧室压力之比/pf需<20（图中青色平面）发动机才能安全工作。从图11 中可以看出，质量流量调节比N 越小/pf越小，调节后 富燃燃 烧室的压力越低，发动机越易实现性能调控目标。在F-O 0.63-0.67、=0.70 的情况下，当N 由4.00 减小到2.00时/pf由18.29 减小至4.68；初始富燃燃气与富氧燃气质量流量比越大，调节后富燃燃烧室的压力越低，在F-O 0.63-0.67、N=4.00 的情况下，当由0.70 增大到2.00时/pf由18.29 减小至12.24。但增大会使得富燃燃气与富氧燃气质量比逐渐偏离化学当量比导致燃烧效率降低，从而造成比冲下降。如表5 中富燃燃气与富氧燃气质量比从0.68 增加至1.75时，发动机比冲从2 072.32 m/s 降低至2 011.53 m/s。N和保持不变时，富燃推进剂（图11（a））和富氧推进 剂（图11（b））的压力 指数越大/pf越小，发动机越容易实现既定的性能调控目标。在N=4.00=0.70 的情况下，当富燃 推进剂压 力指数 由0.50 增大到0.63时/pf由38.95 减小至18.29。因此，为了实现更高的性能调控能力，需要更大的推进剂压力指数。但结合式（8）、式（9）和式（24）计算可知，过大的压力指数会使得推进剂燃速、燃烧室压力等参数对于流量调节阀喉部半径的变化过于敏感，对发动机的稳定工作不利。当调节后富燃推进剂压力指数为0.50时，流量调节阀喉部半径由1.90 mm 减小到1.65 mm，发动机富燃燃烧室压力由5.20 MPa 升高到9.15 MPa，压力升高了3.95 MPa；当调节后富燃推进剂压力指数为0.63时，调节阀喉部半径的相同变化使得发动机富燃燃烧室压力由8.90 MPa 升高到20.00 MPa，压力升高了11.10 MPa。可以预见，当调节后富燃推进剂压力指数继续增大时，调节阀喉部半径的相同变化会使得富燃燃烧室的压力产生更大增幅，从而危及发动机的安全工作。

图11 富燃推进剂压力指数和富氧推进剂压力指数变化对发动机性能调控的影响Fig.11 Influence of pressure index changes of fuelrich propellant and oxygen-rich propellant on performance regulation

4 喷管可调的节流式燃/氧分离发动机

4.1 调控机理分析

结合节流式燃/氧分离发动机几何构型示意图（图4）和不同调节阀喉部半径下其性能参数（表5）可知，经过调节阀调节后的发动机推力调节比为4.112 5时，调节后的富氧燃烧室压力提高至调节前压力的4.04倍，而富燃燃烧室压力却已提高 至20.00倍，即/pf显著大于/po，且 富燃燃烧室已然处于壳体极限承压状态，无法保证发动机安全稳定工作。但降低/pf将导致的降低，无法实现相同的推力调节比。为了同时满足发动机安全性要求和推力调节能力的要求，需使发动机具有更大的即需要增大发动机的/po。

由此可知，调节后喷管喉部面积小于调节前喷管喉部面积，即减小喷管喉部面积能够增大调节后与调节前富氧燃烧室压力之比以及富氧燃气质量流量之比，降低发动机推力调控对富燃燃气质量流量的需求。进而使得调节后在富燃燃烧室压力不显著升高的情况下，发动机仍能够实现相同的推力调节比，从而有效提高发动机的安全性。

考虑到发动机喷管喉部面积变化的需求，在节流式燃/氧分离发动机喷管喉部处设置流量调节阀以对混合燃气进行流量调控。该喷管可调的节流式燃/氧分离发动机几何构型如图12 所示，其喷管喉部半径变化对燃烧室内压力的调节机理与喉栓式变推力发动机［42-43］相似（图12 中Rn为喷管喉部半径）。

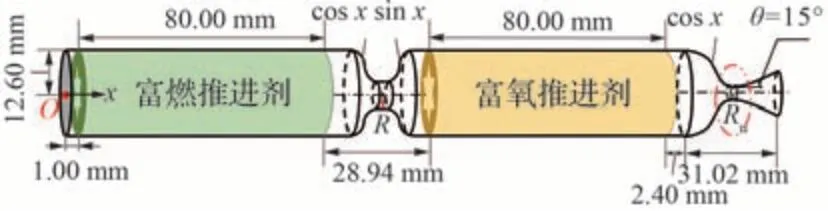
图12 喷管可调的节流式燃/氧分离发动机几何构型示意图Fig.12 Schematic diagram of throttling SFOS with adjustable nozzle

结合质量流量调节比N 以及初始富燃燃气与富氧燃气质量流量比的变化，喷管喉部面积比/At对喷管可调的节流式燃/氧分离发动机性能调控的影响规律见图13。可以看到，减小喷管喉部面积有助于减小发动机调节后富燃燃烧室压力，从而可为发动机提供更安全的工作条件。但当喉部面积减小到一定程度（如图13 中N=3，/At=0.6）时的增加不再对发动机性能调控起到积极作用/pf不随的增加而发生明显改变，从而调节前后的富燃燃气与富氧燃气质量流量之比均保持恒定。当进一步减小喷管喉部面积（如图13 中N=2/At=0.6）时的增加反而增大了富燃燃烧室调节后与调节前的压比。因此，调节后的富燃燃气与富氧燃气质量流量之比相较于调节前更低，推力调控过程中总燃气质量流量的增幅变为主要由富氧推进剂提供。

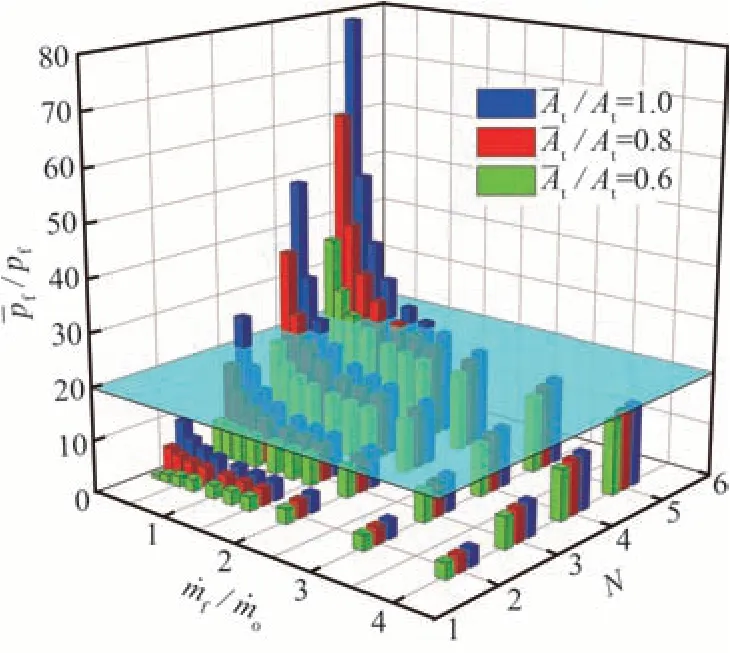
图13 喷管喉部面积变化对发动机性能调控的影响Fig.13 Influence of variation of nozzle throat area on motor performance regulation

4.2 喷管可调的节流式燃/氧分离发动机性能调控机理验证

为了验证喷管喉部面积变化对喷管可调的节流式燃/氧分离发动机内弹道性能的影响，以R-1.65 为基础工况（喷管喉部半径Rn=5.12 mm，记为R-1.65-Rn-5.12），保证质量流率调节比N 相同，计算前后两个调节阀静态工作时不同喷管喉部面积比/At条件下发动机稳定工作状态下的内弹道性能特性。当/At为0.8和0.6时，喷管喉部半径分别为4.57 mm和3.96 mm，相应的流量调节阀喉部半径分别为1.69 mm和1.78 mm，因此，将两种情况分别记为R-1.69-Rn-4.57和R-1.78-Rn-3.96。发动机初始条件及边界条件与2.1 节中的设置一致。

图14 比较了此3 种工况稳定工作状态下的压力、温度、速度和马赫数。喷管喉部面积减小使得富氧燃烧室压力升高（如图14（a）所示），富氧推进剂燃烧产生的富氧燃气质量流量增大，推力调控所需的富燃燃气质量流量减小，因此，富燃燃烧室所需压力降低，流量调节阀喉部半径增大。同时，喷管喉部面积减小使得富燃燃气与富氧燃气质量流量之比减小（更加贴近化学当量比），燃烧更加充分，使得富氧燃烧室内温度升高（如图14（b）所示）。由于两燃烧室之间压差减小，调节阀处燃气流动速度和马赫数减小，喷管出口速度和马赫数增大（如图14（c）和图14（d）所示），因此，发动机比冲得以提高。

图14 调节阀保持静态时不同喷管喉部面积下发动机的流场参数Fig.14 Flow parameters of motor with different nozzle throat areas while valve is steady

表7 列出了喷管可调的节流式燃/氧分离发动机在上述3 种稳定工况下的内弹道参数。结果表明，喷管喉部半径减小，使得富氧燃气的质量流量增大，富燃燃气质量流量减小，两者混合燃烧产生的燃气质量流量（基本不变。富燃燃气与富氧燃气质量流量之比靠近化学当量比，导致燃烧效率升高以及喷管出口燃气速度增加，使得发动机推力和比冲呈增大趋势。在质量流率调节比N 保持不变的前提下，喷管喉部半径由5.12 mm 减小到3.96 mm，发动机富氧燃烧室压力由3.64 MPa 增大至6.40 MPa，发动机富燃燃烧室压力由20.00 MPa 减小至12.76 MPa。这表明喷管喉部半径的减小能够显著降低发动机富燃燃烧室压力，有助于节流式燃/氧分离发动机进行性能调控，因而可为性能调控提供更多方案。

表7 不同喷管喉部半径下发动机调节前后的内弹道参数Table 7 Internal ballistic parameters of motor before and after regulation with different nozzle throat radii

5 结论

本文建立了节流式燃/氧分离发动机内弹道的准一维数值模型，对不同调节阀喉部半径下节流式燃/氧分离发动机调节阀静态工作过程以及不同调节阀作动速度下发动机调节阀动态工作过程对发动机推力性能的影响进行了仿真计算。主要结论如下：

1）静态工作过程结果表明，调节阀喉部半径由2.89 mm 减小到1.65 mm 使得发动机推力从105.09 N 提高到432.18 N，推力提高至调节前推力的411.25%，验证了节流式燃/氧分离发动机的推力调控能力。

2）动态工作过程表明，流量调节阀作动过程中发动机的性能会产生负调现象，4 种不同作动速度下（0.2、1.0、5.0和25.0 m/s）发动机推力的负调量分别为调节前稳定值的5.74%、19.23%、20.05%和20.18%。负调持续时间分别为4.50、3.30、3.00和2.90 ms。调节阀的作动速度越大，负调量越大，但发动机的负调持续时间越短。

3）提出了节流式燃/氧分离发动机性能调控机理的理论关系式。由关系式可知，质量流量调节比N 越小或者初始富燃燃气与富氧燃气质量流量比越大，调节后富燃燃烧室的压力越低；在N=4.00=0.70 的情况下，当富燃推进剂 压力指数由0.50 增大到0.63时，调 节后与调节前富燃燃烧室压力之比/pf由38.95减小至18.29。这表明N和保持不变时，推进剂压力指数越大，调节后富燃燃烧室的压力越低，发动机越容易在其安全工作范围内实现既定的性能调控目标。

4）性能调控机理关系式进一步表明，减小喷管喉部面积能够增大调节后与调节前富氧燃烧室压力之比/po和质量流量之比，使得发动机在降低/pf的情况下仍可实现相同的推力调节比，从而有效提高发动机的安全性。性能调控模拟结果证明，喷管喉部半径由5.12 mm 减至3.96 mm，发动机富氧燃烧室压力由3.64 MPa升至6.40 MPa，富燃燃烧室压力由20.00 MPa降至12.76 MPa，而总燃气质量流量基本不变，发动机推力则由于喷管出口燃气速度增加呈增大趋势。喷管喉部半径减小能够显著降低发动机富燃燃烧室压力，有助于节流式燃/氧分离发动机进行推力性能调控，可为发动机性能调控提供更多可行方案。