超声速下盘缝带伞不同收口方式的气动特性
2024-05-09代雨柔李健薛晓鹏荣伟
代雨柔,李健,*,薛晓鹏,荣伟
1.北京空间机电研究所,北京 100094
2.中国航天科技集团有限公司 航天进入减速与着陆技术实验室,北京 100094
3.中南大学 自动化学院,长沙 410083
盘缝带降落伞在超声速低密度条件下具有优良的阻力性能和稳定性能,结构简单可靠,常用于火星探测器进入减速、地球高空科学探测等用途的减速伞[1]。以火星探测为例,美国从1976—2020 年共成功进行了9 次着陆探测,均使用了盘缝带降落伞[2-5]。在中国天问一号火星探测着陆巡视器进入减速与着陆(Entry,Descent and Landing,EDL)阶段,超声速盘缝带降落伞也起到了至关重要的作用[6]。
随着中国航天事业的发展,超声速降落伞应用领域在不断扩展,性能指标在不断提升,主要表现为被减速物体的质量不断增加,开伞速度不断提高,对降落伞的开伞力、质量与重量的约束越来越严苛。这就要求降落伞在大幅增加面积和提高强度的同时,要尽可能降低开伞力,减小重量和体积。
收口技术是解决上述工程问题的有效途径之一。该方法在充气过程中可有效控制降落伞的阻力特征,使降落伞逐级打开并可以抑制降落伞的过度充气。该技术已在亚声速领域得到了很好的应用,神舟系列飞船的减速伞和主伞均采用1 次收口开伞方法,以控制各级开伞过载不超过规定的限值要求[7]。但是在超声速领域,该技术还未得到工程应用,国内外仅做过少量的空投试验。超声速高空降落伞试验室(SHAPE)在马赫数>2.5 的情况下,使用细长体和钝体前体对收口降落伞进行了飞行试验。相比于细长体,钝体后面的收口降落伞由于前体尾流的影响,出现了破损的情况[8-9]。数值模拟方面未见相关文献公开发表。由此可见,现阶段缺乏关于超声速收口盘缝带伞有效的数值模拟方法,和关于不同收口比下的收口盘缝带伞气动表现的系统性研究。所以,关于盘缝带伞超声速收口技术的应用需求是迫切的,现有研究工作不满足未来工程应用需求。
对比亚声速收口降落伞,超声速收口降落伞所面对的主要问题是:流场更加复杂,前体与降落伞间的干扰加剧,使得伞衣出现强烈的“呼吸”振动现象,有可能造成伞衣塌陷、结构破坏,导致减速失败。本文以不同收口方式的盘缝带伞为研究对象,采用流固耦合方法进行数值模拟,对比不同收口方式的盘缝带伞的开伞和呼吸过程,总结不同收口比下的气动特性规律,为超声速收口盘缝带伞的工程应用提供技术支撑。
1 研究对象
1.1 收口盘缝带伞
盘缝带降落伞是开缝伞的一种,伞衣由一个中心有通气孔的圆“盘”和圆筒型“带”组成。降落伞收口的常用方法是使用收口绳进行收口。该方法通过将收口绳用收口环固定在伞衣周向位置,从而对伞衣的充气过程起一个限制作用。同时,收口绳上也会放置切割器,用于在规定时间解除收口[1]。由于盘缝带伞的伞衣结构特殊,收口绳可以安装在“盘”或者“带”的边缘,即盘缝带伞的2 种收口方式,“带”收口和“盘”收口,如图 1所示[10]。
1.2 降落伞参数设置
使用美国“海盗号”的4%缩比伞为研究对象,该伞已有公开发表的相关试验数据,可用于对比分析。其具体尺寸和相应尺寸分别如表 1和图 2 所示[11]。

表1 盘缝带伞结构尺寸Table 1 Structural size of disk-gap-band parachute 单位:m
数值模拟过程中,降落伞的伞衣材料设置为薄壳单元,伞绳和加强带选用离散的梁/索单元,伞衣与伞绳处于初始拉直状态。返回舱外形参考EXOMars 计划的钝体航天器模型[12],由一个半锥角70°的钝头前体和一个半锥角为45°的圆锥后体组成,使用薄壳单元搭建。返回舱的单元空间固定。整体结构如图3 所示。
1.3 降落伞收口参数设置
工程上常用收口直径比(也称收口比)来定量描述收口程度,该参数为收口绳长度与伞衣底边长度之比,也可以表示为收口绳直径和伞衣名义直径的比[13]。使用收口绳直径和伞衣名义直径比定义收口比,对马赫数分别为1.6和1.8 时不同收口方式的不同收口比进行数值模拟,其中以马赫数1.8 环境下的数值模拟结果作为主要研究对象,以马赫数1.6 环境下的结果作为验证对象。具体研究算例如表 2 所示。

表2 研究算例Table 2 Research examples
2 来流条件及研究方法
2.1 来流条件
以未来火星低密度大气减速为需求背景,为更好地贴近真实的火星大气环境,参照火星科学试验室(Mars Science Laboratory,MSL)的探测巡视器着陆火星过程中其速度与离火星地面高度的对应关系[14]和NASA 给出的根据火星全球勘探者(Mars Global Surveyor)对火星大气进行测量得到的拟合公式[15],计算出本研究使用的火星大气参数,如表 3 所示。

表3 仿真使用来流条件Table 3 Freestream condition for simulation
2.2 网格无关性验证及流场域模型
选取单个降落伞进行网格无关性验证,对单元长度为0.05、0.04、0.03、0.02 m 的流场网格进行数值模拟计算。计算得到的降落伞的阻力系数如表 4 所示,以0.02 m 为基准算例,得到各算例的误差。给出不同网格长度与阻力系数的关系图,如图 4 所示。与网格大小为0.02 m 的算例对比,各阻力系数的误差均在10%以下,根据图 4 所示结果,在网格数为0.02 m时,计算结果已收敛。同时对比图 5 所示0.04、0.02 m 网格的局部速度云图,观察得到,尽管2 种不同大小的网格都能够很好地展示降落伞后的不定常宽尾流。但相比于0.04 m 的网格,0.02 m 能够更好地捕捉到降落伞顶孔的高速射流,流场细节更加清晰。所以在综合考虑计算精度与时间成本的情况下,网格长度选取0.02 m。
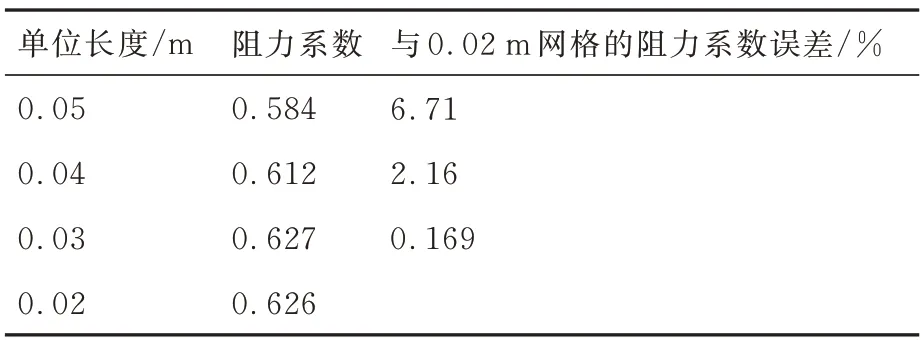
表4 网格无关性验证Table 4 Grid independence verification
所取得的流场域沿降落伞轴向、法向、侧向的长度分别为5 m×3 m×3 m。最终六面体的流场域划分为约526 万个网格,建立的流场计算域及仿真模型的整体网格结构如图 6 所示。由于伞衣面积小,开伞速度快,仿真流场采用理想气体模型且采用如表 3 所示的恒定大气密度和压强进行仿真。流场顶端和壁面添加无反射约束,用以模拟远场状态,使仿真结果与实际无限质量开伞情况更为接近。
2.3 研究方法
降落伞流固耦合的研究一直是一个挑战,为了模拟柔性降落伞的开伞和开伞后伞衣呼吸的全部过程,需要对流场中的激波和尾流进行良好的模拟。时-空守恒元解元(CE/SE)方法是一种物理概念清晰、计算精度高、格式构造简单的流体力学方法[16],具有广阔的发展前景。该方法由Chang 提出,由刘海焘等进行改进,可求解间断流场CE/SE 格式的三维Navier-Stokes(N-S)方程,具有较高的分辨率。求解方法往往分为以下4步[17-21]:
步骤1在完全气体的一维情况下,给出量纲为1 的非定常N-S 方程,并定义不同空间位置的离散点,如图 7 所示的A1、Q、A2[21]。之后,在一维离散的基础上将时间作为额外的空间维度,构建二维欧拉空间域E2,并建立该欧拉空间的坐标,令x1=x,且x2=t,则
步骤2利用高斯散度定理,将时间和空间完全统一,微分方程为
式中:S(V)是E2中任意区域V 的边界。
步骤3建立SE,沿图 7 所标定的时间空间的内部边界,沿SE 域对流体变量进行近似的泰勒级数展开式进行逼近,令
同理可得:
步骤4将步骤2 所得式(2)用式(7)逼近,并将式(3)~式(5)代入,得到式(8):
此时在每个网格点的变量只有um和umx,将图 7 所示的2 个守恒元CE-和CE+的变量代入式(8),得出计算结果。
所使用的DUALCE/SE 方法(dual-mesh CE/SE,又可简称为双网格CE/SE 方法),对传统的CE/SE 算法进行了小范围的改进。传统CE/SE方法求解器的流体变量都在网格的中心点上,而DUALCE/SE 方法采用双网格交替在流体单元中心和流体单元节点上求解流体状态变量。在采用相同的网格数下,该方法更为精确[22]。
试验中,开伞的动态过程采用DUALCE/SE方法计算流场,固体结构分析使用有限元方法,两者交替进行计算。流固耦合部分使用浸入边界法来处理。浸入边界法是一种数学建模方法,该方法在生成网格时不需要生成复杂的贴体网格,只需要生成正常的笛卡尔网格[23]。而针对充气后的稳定形态,采用计算流体力学方法进行分析。
3 仿真模型准确性验证
此前,已有部分学者使用时-空守恒元解元方法对超声速降落伞的开伞过程进行了仿真,并得到了较为准确的结果[24-26]。本节的研究对象是在马赫数1.6 的火星大气条件下,对上述降落伞在不收口情况下展开的数值模拟结果,从阻力系数、伞衣充满过程的外形变化方面和已有试验结论进行对比。另外,超声速高空降落伞试验室(SHAPE)在1971 年进行了超声速收口降落伞的飞行试验,本文将对比收口降落伞的阻力系数、投影面积及气动外形的相关数据。
如图 8 所示,在马赫数1.6时,数值模拟计算出的阻力系数平均值为0.60。图 9 所示为NASA 综合风洞、高空开伞、飞行试验结果,给出的盘缝带伞阻力系数随马赫数的变化曲线,中心线为标称值,上下为偏差范围[27]。其中,在马赫数1.6时,阻力系数的高值为0.82,中值为0.66,低值为0.50。选取中值作为参考,数值模拟所得阻力系数位于预测阻力系数之间,并接近中值。
图10 所示是先进超声速降落伞充气研究试验(ASPIRE)在2019 年所做的盘缝带伞高空开伞试验的降落伞的展开仰拍图[28]。图中从左至右依次为伞绳拉直降落伞开始展开的时刻、降落伞张开过程中的时刻和降落伞首次张开的时刻。从图中可以看出,虽然展开时间有所不同,但是3 组展开图都是盘的部分先打开,之后带的部分再打开。图 11 所示是数值模拟的结果,图中从左到右所展示的降落伞外形的顺序与图 10 相同,数值模拟结果与实际情况一致。
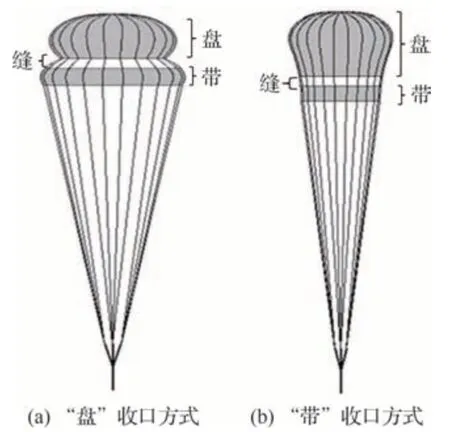
图1 盘缝带伞的不同收口方式[10]Fig.1 Different reefing ways of disk-gap-band parachute[10]
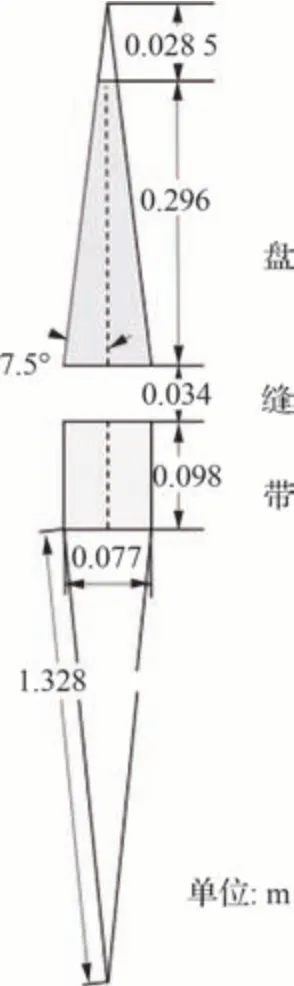
图2 盘缝带伞结构图[11]Fig.2 Disk-gap-band parachute structure[11]

图3 盘缝带伞模型Fig.3 Disk-gap-band parachute model

图4 不同网格大小的阻力系数Fig.4 Drag coefficients of different mesh sizes
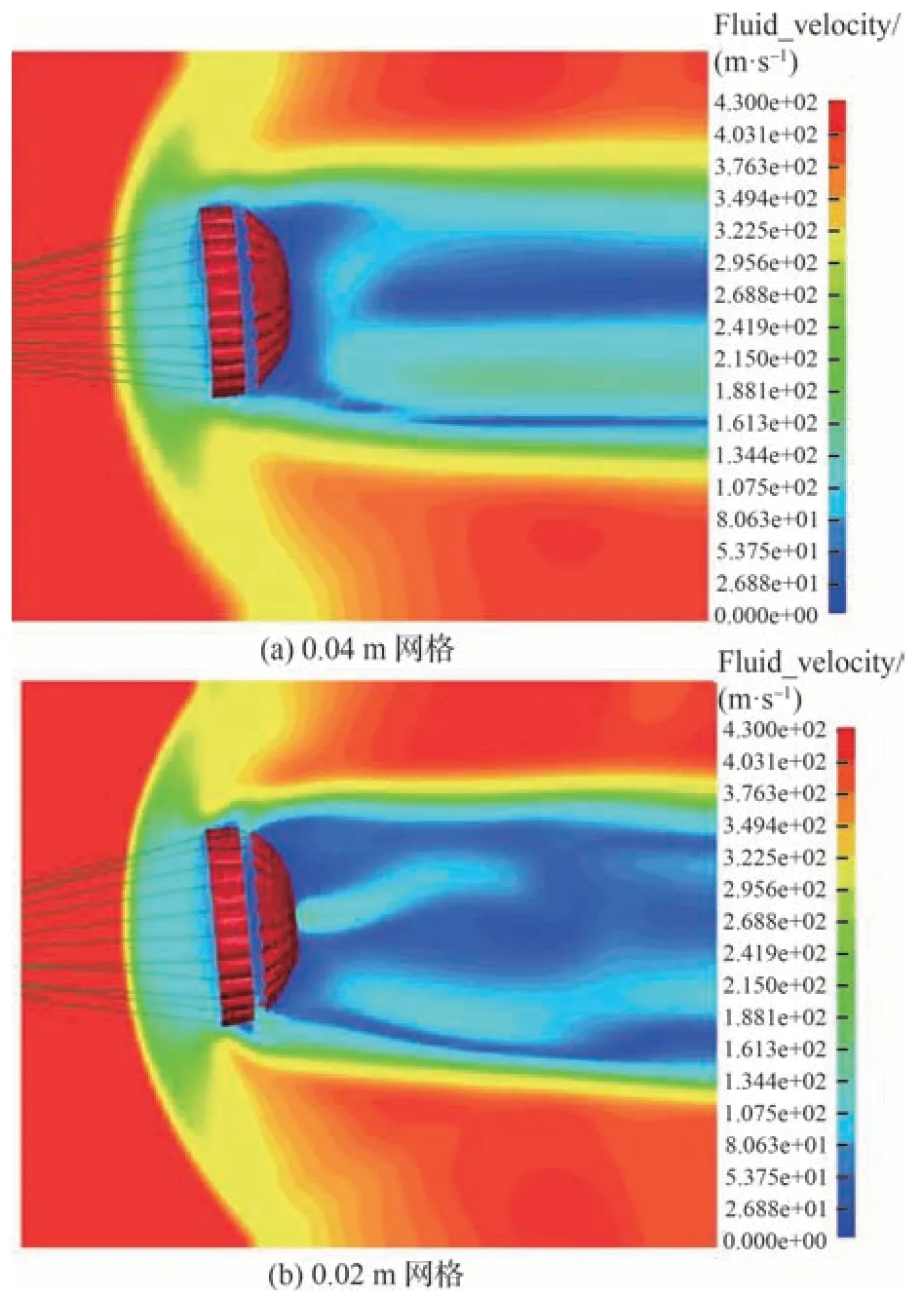
图5 速度云图Fig.5 Velocity contour
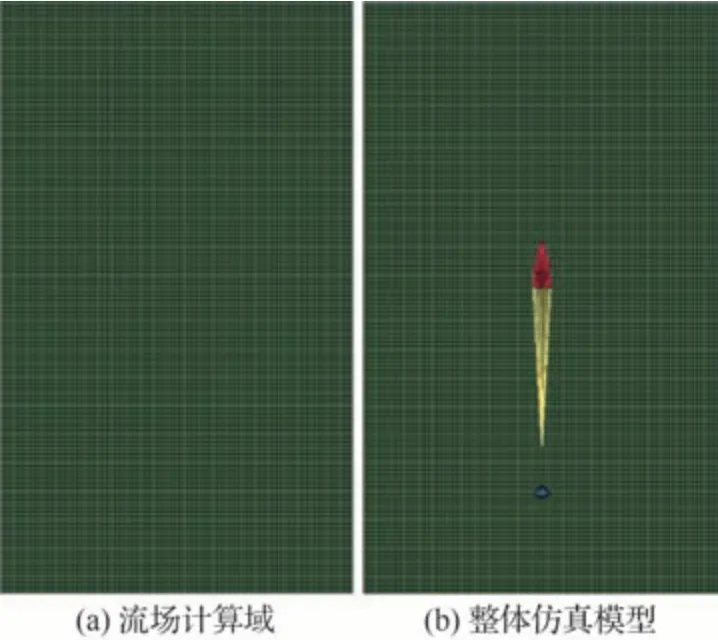
图6 仿真模型网格结构Fig.6 Grid structure of simulation model

图7 CE/SE 一维求解空间域[21]Fig.7 CE/SE one-dimensional solution space domain[21]

图8 阻力系数仿真时间历程曲线Fig.8 Simulation time history curve of drag coefficient
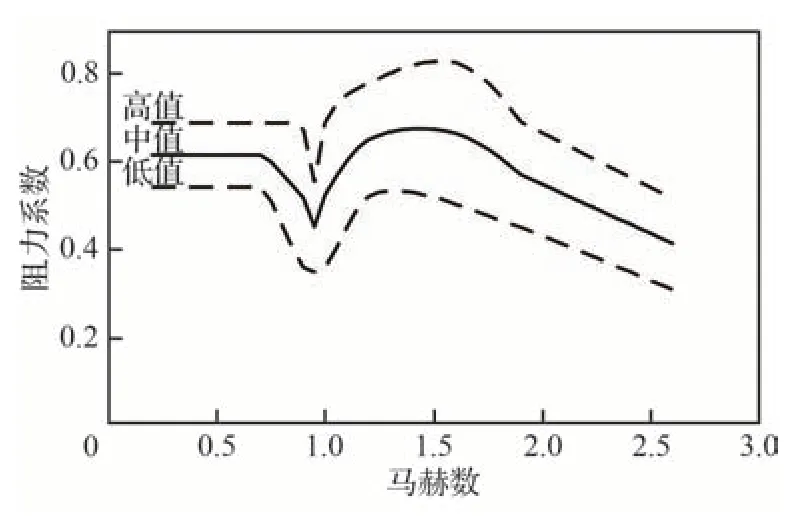
图9 不同速度下阻力系数范围Fig.9 Range of drag coefficient at different speeds

图10 探空火箭降落伞展开图[28]Fig.10 Inflation process of sounding rocket parachute[28]

图11 数值模拟降落伞展开过程Fig.11 Inflation process of numerical simulated parachute
对于超声速收口盘缝带伞的准确性验证,超声速高空降落伞试验室(SHAPE)的飞行试验得到了在收口比约为29%的情况下,不同马赫数下的阻力系数,如图12 所示[8]。其中马赫数为1.8时,阻力系数为0.211。另一试验项目得到了同大小的盘缝带伞不收口情况下,马赫数为1.8 时的阻力系数为0.535[29]。将两者对比,得到在收口情况下阻力系数占未收口情况下阻力系数的39.4%。该文章也提供了降落伞在马赫数为1.8时的阻力面积比(伞衣收口状态的阻力面积与完全张满伞衣的阻力面积之比[13])为50%。将该数据与数值模拟结果对比,见表 5。试验结果与数值模拟结果误差小于10%。同时该试验室也提到,在降落伞展开之后,伞盘部分基本保持稳定,呼吸作用主要为伞带部分发生膨胀和收缩。本文数值模拟的结果与该文描述一致相同,具体气动特征见本文4.1节。
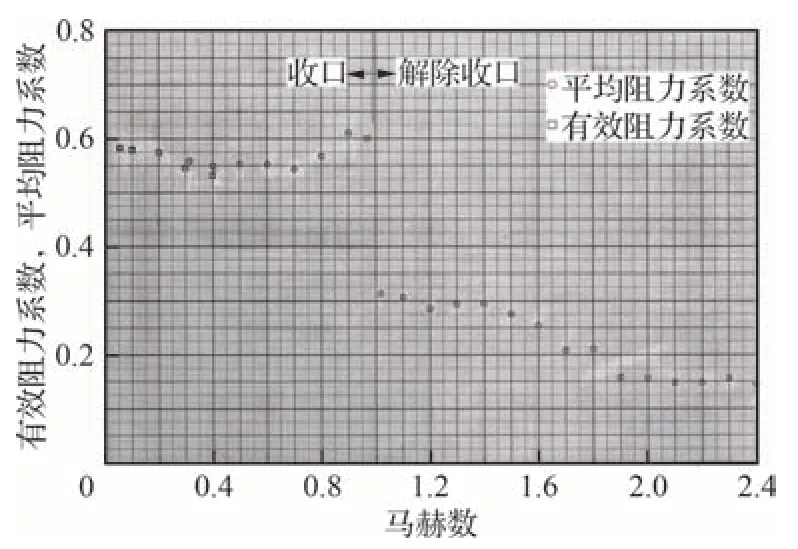
图12 飞行试验所得阻力系数[8]Fig.12 Drag coefficient of flight test[8]

图13 盘收口盘缝带伞相关结果Fig.13 Relevant result of disk-gap-band parachute with mid-gore reefing
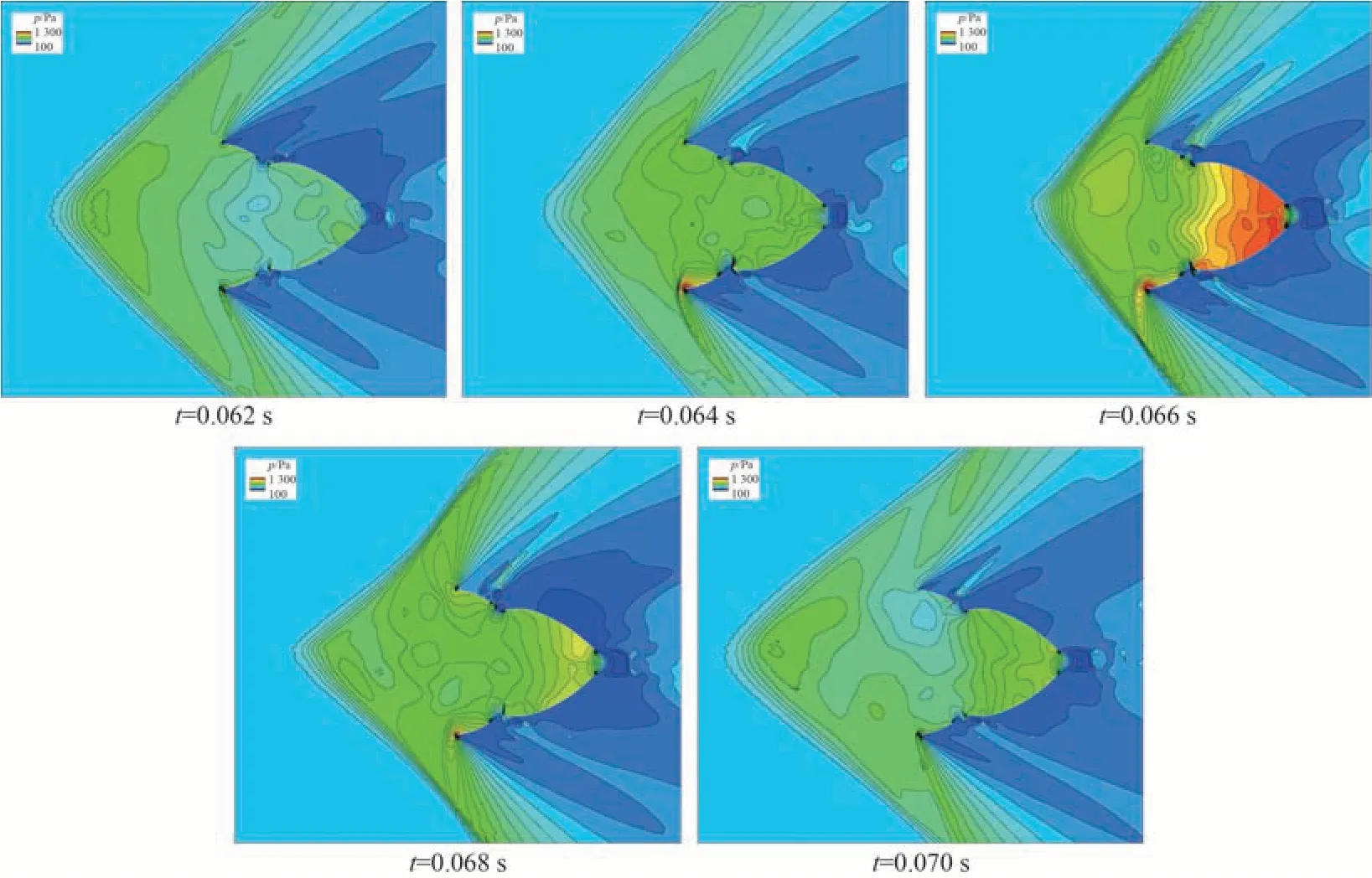
图15 盘收口降落伞压力云图Fig.15 Pressure contour of disk-gap-band parachute with mid-gore reefing

图16 带收口盘缝带伞相关参数Fig.16 Relevant parameter of disk-gap-band parachute with skirt reefing

图17 带收口降落伞不同部分阻力系数Fig.17 Drag coefficients of different parts of disk-gapband parachute with skirt reefing
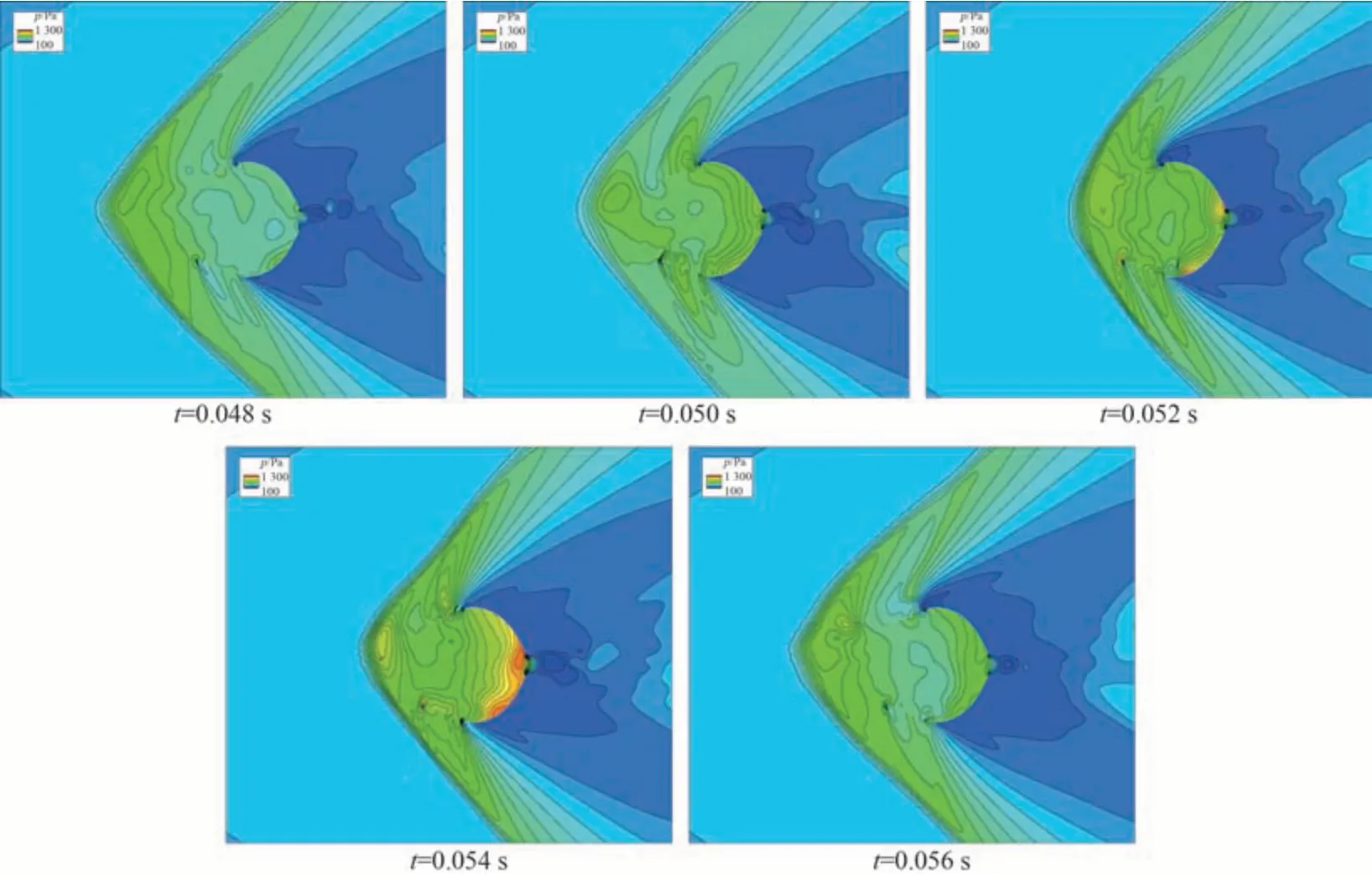
图18 带收口降落伞压力云图Fig.18 Pressure contour of disk-gap-band parachute with skirt reefing
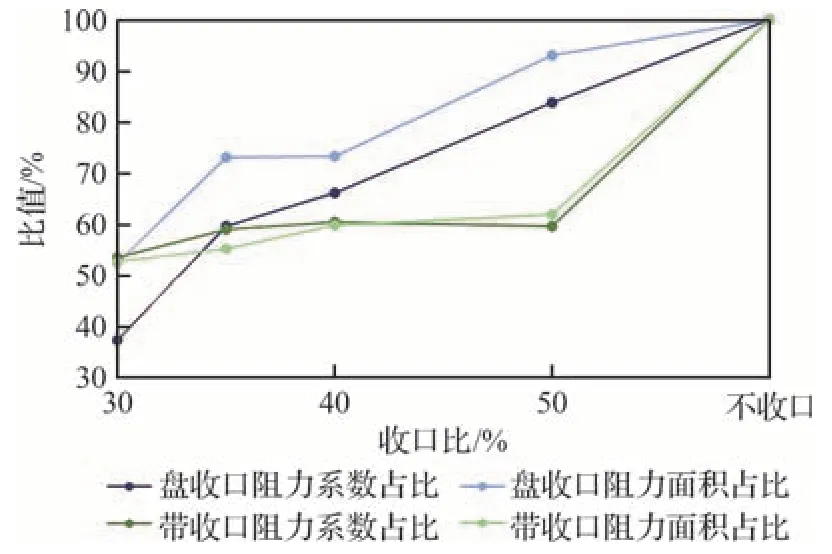
图19 不同收口比下的参数比值Fig.19 Parameter ratio of different reefing ratio
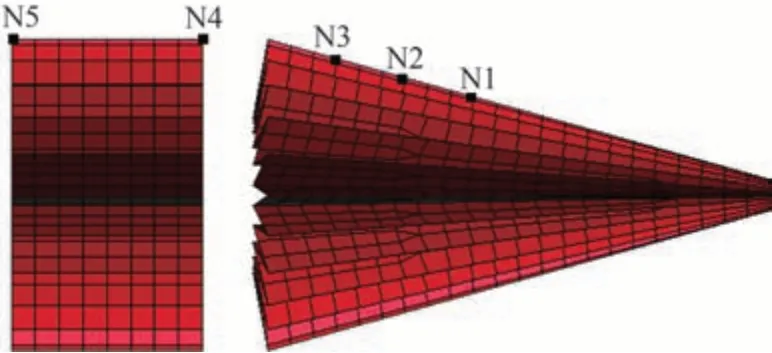
图20 降落伞点位图Fig.20 Different positions on parachute
由不收口降落伞的开伞外形和阻力系数以及收口降落伞的阻力系数,投影面积和气动外形的对比,可以证明:本研究采用的数值模拟方法是有效的,计算结果是可靠的。
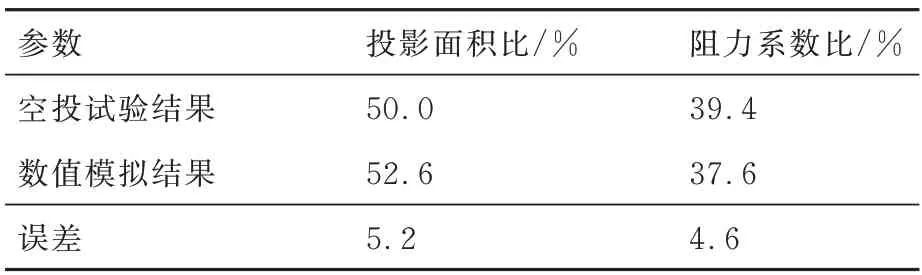
表5 参数对比Table 5 Parameter comparison
4 不同收口方式的影响
4.1 不同收口方式开伞和呼吸方式对比
4.1.1 盘收口
本节总结了收口比为30%的情况下收口绳的受力与时间的关系图、降落伞上不同点的投影面积与时间的关系图以及降落伞在呼吸过程中不同时间的仰视图,如图 13 所示。
在盘收口的开伞和呼吸过程中,降落伞的盘和带表现出不同的气动特点。降落伞的收口绳在约0.06 s 时第1 次收紧,在此之后的0.02 s内,降落伞盘部分点位的投影面积达到最大值,在这之后,盘部分点位的投影面积几乎保持不变。而带部分在收口绳第1 次收紧之后,该部分点位的投影面积依旧持续增大,直到约0.11 s 达到最大值。之后在0.192 s时,带部分点位的投影面积到达第1 个波谷位置。在这个位置,收口绳受力也有一定的减小,这说明带的收缩运动也微小地带动了盘边缘的收缩。之后在约0.21 s 的位置收口绳的受力再次增加,随后带的部分也再次张开,投影面积在0.24 s 时达到了第2 次膨胀的最大值,并在0.26 s 时出现了小范围的波动。从波峰波谷对应的伞衣结构仰视图也可以看到,在盘收口降落伞开伞的时候,盘的部分先充满,之后带的部分再逐渐张开。在降落伞呼吸的时候,盘的部分基本保持充满状态,而带的部分发生不规则的膨胀和收缩。
流固耦合计算对流场中的激波、压力捕捉精度有限。为了分析前体尾流与伞前激波的相互作用过程,使用计算流体力学的方法,提取收口比为30%的降落伞稳定后的平均外形,并假设该降落伞为不透气刚体进行计算。算法基于密度求解器,采用有限体积法进行空间离散,使用三维可压缩理想气体N-S 方程为控制方程,仿真采用层流进行计算。图 14 所示为使用计算流体力学方法所得到的盘部分、带部分和整体受到的阻力系数。图 15 所示为时间取0.062~0.070 s 这一个压力周期内降落伞周围的压强云图。在0.062 s时,降落伞阻力系数在波动周期的波谷,伞内处于一个相对低压状态,随着时间的推进,伞前激波顺流向推进,导致降落伞伞内的压力升高。当伞内压强增高到一定值后,伞内高压会推动伞前激波逆向移动,致使伞内压强再次降低,继而完成一个周期。从云图中可明显看到,在不考虑织物透气性的情况下,收口绳和降落伞盘的部分形成了一个只有顶孔透气的伞包,伞盘中积累的高压只能通过降落伞盘和带之间的缝隙流出,所以该结构特点导致降落伞的伞盘部分始终处于充气状态。另一方面,虽然降落伞“缝”的位置形成了一个泄压口,但由于伞后的膨胀波位置位于带的外边缘,导致带的部分始终存在较高的内外压差,从而使得该部分在开伞时会有一个较大的波动。
4.1.2 带收口
收口比为30%的带收口的收口绳受力和阻力系数如图 16 所示,为了主要关注收口降落伞的开伞和呼吸过程,本节只截取上述参数0~0.4 s时间的数值。可以观察到,收口绳受力在0.074 s时达到了第1 个峰值,但是最大投影面积还处于上升阶段,在0.088 s 左右投影面积上升到最大值。收口绳受力在0.174 s 时达到了第2 次最大值,而投影面积则在0.182 s 时达到了第2 次的最大值。投影面积的最大值和收口绳受力的最大值的时间较为统一,但是投影面积的峰值要比收口绳受力的峰值出现的稍晚,这主要是因为在带收口的降落伞充气的时候,盘的边缘部分要先于带的部分张开,然后通过伞绳带动带的部分向四周张开,在带的部分张开至收口绳完全撑开的时候,伞盘边缘继续张开直到最大程度后开始回弹。随着时间的推进,收口绳受力和投影面积也越来越趋于稳定。从不同点的投影面积可以看出,除第1 次投影面积达到最高值的时候外,其他情况下,30%带收口降落伞的最大投影面积位于N3 的位置,N4和N2 位置的投影面积大小随降落伞的呼吸作用来回交替变换,所以带收口的开伞和呼吸过程是整个降落伞一起展开和收缩的过程。
同样,使用计算流体力学的方法,对30%带收口降落伞的平均气动外形进行了分析。图 17所示为使用计算流体力学方法所得到的盘、带和整体受到的阻力系数,并对自0.048~0.058 s 的降落伞周围压强部分进行分析,如图 18 所示。从压力云图中可以看到压力增强与激波移动的周期。但是和盘收口不同的是,带收口的膨胀波在盘的边缘,而不是带的边缘。这种特殊的结构使得带的部分被包裹进了高压区域,并使得该部分并没有起到相应减速的作用,而各部分的阻力系数图也同样证明了这点。并且,从阻力系数图也可以看到,带收口的时候,降落伞盘部分的阻力系数和伞衣整体的阻力系数几乎相同,而带部分受到的力在正向力与负向力之间来回波动,这也会导致带部分的不稳定。
4.2 不同收口方式的气动规律
首先,使用数值模拟方法计算出不同收口方式和收口比的阻力系数和投影面积,为了更好地对比不同数据间的关系,对阻力系数和投影面积做以下处理:将不同收口方式的不同收口比的阻力系数除以不收口降落伞稳定后的阻力系数,同理,将不同收口方式的不同收口比稳定后的平均投影面积除以不收口降落伞稳定后的平均投影面积,得到如图 19 所示的关系。从图中可以看出,盘收口方式的阻力系数比和投影面积比随着收口比的增大而增加,其中在30%~35%的过程中,投影面积占比和阻力系数占比增加的幅度较大,但是35%~40%之间,投影面积并没有明显增大。这主要是因为,在35%的收口比时,数值模拟时降落伞发生了较为严重的自旋状况,随着自旋速度的增加,降落伞的伞衣向离心方向扩展,使得该伞的整个气动外型变得更加扁平,投影面积也相应增大。从数据分析来看,这种现象也间接使得降落伞的阻力系数有所增大。但整体来看,盘收口投影面积的占比始终比阻力系数的占比要大,并且能够保持近似同步的增长幅度。
降落伞带收口方式的结果有所不同,无论是阻力系数的比值还是投影面积的比值,收口比在30%~50%时,降落伞的投影面积和阻力系数改变都不明显。为了探究该现象的原因,收集了不收口和30%、35%、40%带收口在降落伞不同位置点位的投影面积大小,计算其对应的近似圆的直径长度,并与名义直径做比,点位图如图 20 所示,结果如表 6 所示。表中数据表明,在这几种收口比下,降落伞的最大投影面积的位置(表中加粗数据)由N2 位置逐渐转移到N3 位置,表明降落伞的外形随着收口比的增加而变化,但是最大投影面积的值并没明显差别,并且跟不收口降落伞的投影面积相差较大。结合图 19 可以看到,这些投影面积的改变并没有引起阻力系数的明显增加。
为了解释这一现象,从降落伞结构、伞内压力和伞衣的结构孔隙率方面进行说明。首先,从降落伞的结构方面分析,带收口时降落伞的最大投影面积的位置位于N3 或N2 点位。所以,如图 21 所示,带收口时降落伞的伞衣形成了一个翻折,伞顶到伞底这段长度形成了图中蓝线所示的曲线,这里称为迎风面和背风面。于是,当降落伞底部的收口绳增长时,也就是降落伞的底部横向周长增加时,因此而导致的纵向长度的增长会同时被分配到迎风面和背风面2 面上,导致收口绳的增加对降落伞的阻力面积的影响很小。其次,由上文所给的带收口降落伞的压力云图及不同部分的阻力系数可以看到,在带收口的情况下,伞带的部分被包裹在了伞前高压中,这个时候伞带受到的平行于来流的力非常小,即相当于伞带的部分没有为降落伞的阻力提供任何帮助,导致阻力系数增加不明显。最后,从降落伞的结构透气性并结合上文所展示的伞内压力变化来解释这一现象。降落伞膨胀的本质就是在孔隙率低的地方形成高压区域。如上文提到盘收口是将降落伞的盘部分围成了小型的伞包,若将该伞包的结构透气性等效为该结构的有效孔隙率,结合前文所给参数可以计算出该伞包的有效孔隙率仅为0.77%。而带收口所形成的整体部分的有效孔隙率为11.98%。因而超声速情况下,有效孔隙率更大的情况会使得来流更易流出,更难形成较高的内外压差,也导致降落伞的阻力系数增加不明显。
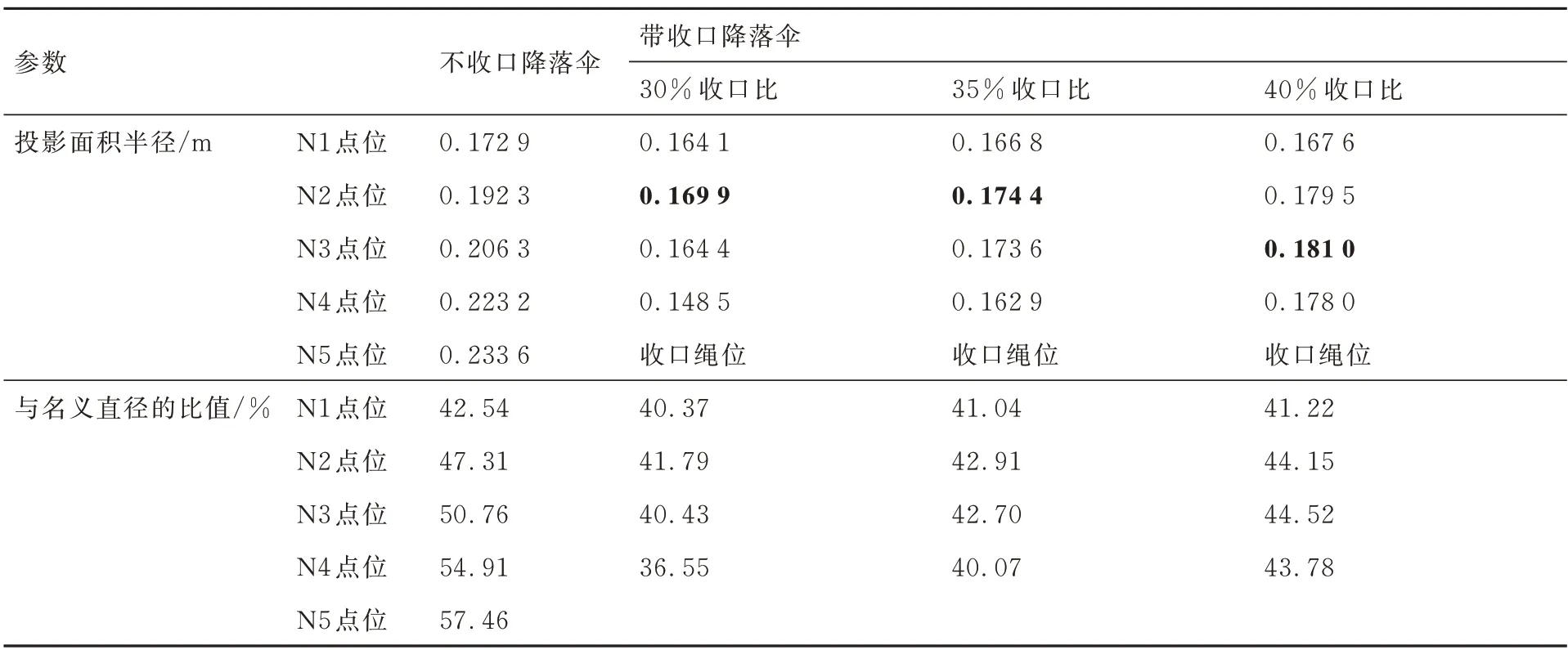
表6 不同点位降落伞投影面积及比值Table 6 Projected area and its ratio of parachute at different positions
5 结论
基于流固耦合算法,得到了在收口比相同的情况下不同收口方式开伞和呼吸过程的特点,并得到了不同收口方式不同收口比的阻力系数和投影面积的关系,及其普遍气动特点。现总结如下:
1)在盘收口降落伞开伞时,盘部分首先充气,之后降落伞的带部分再逐渐张开。降落伞呼吸的时候,盘的部分基本保持充满状态,带的部分发生不规则的膨胀和收缩。
2)在带收口降落伞开伞的过程中,盘的边缘部分要先于带的部分张开,然后带动带的部分向四周张开。呼吸过程是整个降落伞一起展开和收缩的过程。
3)盘收口方式的投影面积的占比始终比阻力系数的占比要大一些,自30%~50% 的收口比,两者皆随着收口比的增大而增大,并保持近似同步的增长幅度。
4)带收口方式的阻力系数的比值和投影面积的比值在收口比为30%~50%之间并没有明显变化,这主要是因为相比起盘收口,带收口的带部分没有起到阻力的作用,且结构孔隙率较大,相比盘收口,伞内外没有形成较大的压强。
5)在马赫数1.8下,收口比相同时,盘收口能够提供更大的阻力系数。结合文章所给数据,初步建议:盘收口的收口比应在50%以下,因为该收口比以上的收口阻力系数已非常接近全展开情况的阻力系数,收口绳已没有明显作用。
