基于支座位置拼装误差的无应力线形修正分析

■刘 昊

（青岛市交通规划设计院有限公司，青岛 266000）

自1959 年在奥地利的阿格尔桥首次成功应用顶推施工以来，顶推法在桥梁施工中广泛应用[1-3]。采用顶推施工的桥梁按照梁体的无应力线形在拼装平台上进行梁段的拼装[4-6]，梁体的无应力线形决定了桥梁成桥状态的线形、受力和通车运营的舒适程度[7]。 在梁段拼装阶段，受施工误差、大温差、焊接变形等多种因素影响[8-9]，梁段拼装不可避免地存在误差且线形偏位不可逆转[10]，后续待拼梁段应考虑梁体线形偏位修正， 若不及时调整误差， 会造成误差累计， 使得全桥几何线形偏离设计线形过大，从而影响桥梁安全和正常运营[9]。 因此，及时、有效地对实际线形误差进行评估，是调整后续梁体拼装线形参数的重要步骤，也是实现高精度梁体无应力线形的重要环节。 基于此，本文提出一种相对于支座位置的拼装误差计算方法， 考虑已拼梁段拼装误差、温度变形和焊缝收缩对处于拼装状态梁段的影响，明确线形误差修正，并以矩阵的形式描述各个工况下的梁体线形并推导线形之间的传递关系，最终对理想状态下的传递矩阵进行实时动态修正，以达到对梁体线形的高精度控制。

1 顶推桥梁几何线形描述

1.1 梁体几何线形描述

对于采用拼装施工的梁体，一般采取以折线代替曲线的方法，将各个梁段加工成直线形状在现场拼装，如图1 所示。 假设组成梁体的拼装梁段段数为n，每个梁段首尾两端各设置1 个测量控制点，前面一个梁段末端控制点同时也作为后面一个梁段的前端控制点，共计n+1 个控制点，控制点编号顺序从前至后依次为1，2，…，n+1；梁段轴线和水平线的夹角为αi（i=1，2，…，n+1）；梁段编号顺序从前至后依次为1，2，…，n，相应梁段长度为Lj（j=1，2，…，n）；对梁体的支座位置从前至后进行编号，支座位置控制点序号为Pk（k=1，2，…，n）。

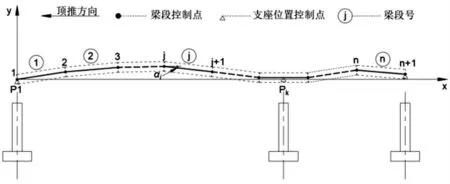
图1 梁体无应力线形及各控制点位置示意

以梁段1 前端控制点1 为坐标原点建立笛卡尔直角坐标系，后续各控制点坐标以向量Φi=[xiyi]T表示，根据几何关系进行计算可得：

1.2 各工况线形矩阵表达

梁段的线形在梁段拼装的不同工况下会呈现不同的线形，需对各个工况下的梁段线形进行分析，以确定当前梁段拼装的线形是否合理以及计算后续梁段的拼装坐标；因此，非常有必要对梁段拼装这一工况细分。 将梁段拼装线形细分为5 种线形：

理论无应力线形是基于成桥线形和预拱度确定的梁段各控制点理论坐标，通过连接各控制点理论坐标形成理论无应力线形。 焊后实际线形是根据理论无应力线形进行梁段拼装后各控制点的实测坐标。 焊后拼装线形是在梁端焊接完、顶推前的工况下分析线形， 考虑梁段拼装可能产生的误差、预测后续梁段拼装可能的温度变形和焊缝收缩而得到后续梁段拼装的各控制点理论坐标。 顶推后实际线形是焊后实际无应力线形在顶推过程中的变化，即经过刚体平移和转动后已拼梁段各控制点的坐标。 顶推后拼装线形是焊后拼装线形在顶推过程中的变化，即后续梁段拼装的各控制点坐标。

1.3 梁体刚体位移描述

梁体按无应力线形拼装梁段，拼装后的梁体向前顶推，确保后续梁段拼装的进行。 拼装后的梁体无应力线形形状不变，顶推相当于刚体平移和转动（见图2）。由于后续梁段拼装与前一批拼装梁体的最后一节梁段位置和末端转角有关， 可将无应力线形视为随已拼装梁体的末段梁发生刚体平移和转动。本文将前一批拼装梁体的末段梁称为控制梁或控制梁段，设该梁段首尾两端控制点分别为A、B 控制点。

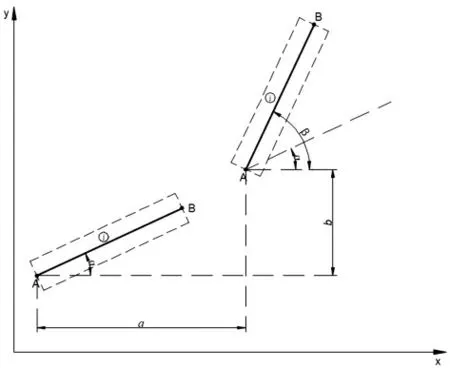
图2 刚体位移示意

图中α 为梁段j 与水平线的夹角，a 为梁段j 沿x 方向的平移量，b 为梁段j 沿y 方向的平移量，β为梁段经过刚体转动后与水平线的夹角。 于是梁段j 上任意一点Φ=[x y]T经过图2 所示的刚体平移和刚体转动得到Φt=[xtyt]T，有关系式：

式中：T 为刚体旋转矩阵，U 为刚体平移矩阵。

2 梁体拼装误差描述

由于施工误差、温度变形、焊缝收缩等因素使得拼装出来的梁体线形和理论无应力线形不可避免地存在误差，故需对误差逐一分析，尽量减小误差。 记总误差由温度变形误差、焊缝收缩误差、梁段拼装误差组成，为Δ=[Δx Δy]T，Δx 为x 方向产生的误差，Δy 为y 方向产生的误差，则温度变形误差、焊缝收缩误差、梁段拼装误差分别用Δ1，i、Δ2，i、Δ3，i表示。

2.1 温度变形误差Δ1，i

梁段拼装时由于顶、底板温度不一致产生不均匀温度场，不均匀温度场产生的温度效应使得梁段产生不均匀的变形。 若进行梁段拼装时不考虑温度变形的影响，会使梁段拼装的实际线形和理论值产生误差。 温度变形可按式（6）计算：

式中：μ 表示钢材的线膨胀系数；ΔT 表示箱梁顶、底板温度差。

2.2 焊缝收缩误差Δ2，i

钢结构焊接时，由于焊接是一个不均匀的加热过程，焊接完的钢结构在焊缝区域会产生残余应力，焊缝温度逐渐冷却至室温的过程中，由于热胀冷缩会使焊缝产生一定的收缩变形。 因此梁段拼装时需考虑焊缝收缩产生的误差。 焊缝收缩变形可按式（7）计算：

式中：ω0表示现场1 条焊缝的平均收缩量。

2.3 梁段拼装误差Δ3，i

梁体全部拼装完和顶推完后，梁体最终要落在支座位置上，若各个控制点相对于支座位置控制点的实际相对高程与理论相对高程不一致，均会造成梁体在支座位置的强迫位移，降低梁体的受力安全（图3）。因此，各个控制点的拼装误差计算以相对于支座位置实际相对高程和理论相对高程的差值为准，以此差值参数来控制后续梁段的拼装，尽可能地减小梁体的强迫位移。因此，梁段各控制点误差为：

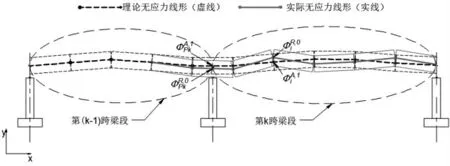
图3 梁段拼装误差示意

3 梁体拼装

梁厂预制好梁段后运送到现场拼装平台上，按照梁体拼装无应力线形并考虑误差的影响，控制各梁段控制点就位高程后，进行梁段的拼装。 顶推施工桥梁拼装无应力线形实现的步骤如图4 所示。

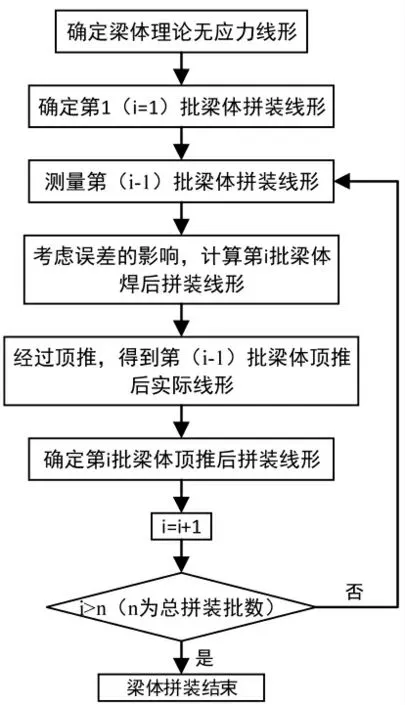
图4 顶推梁体拼装无应力线形的确定步骤

3.1 第1 批梁体拼装

第1 批梁体拼装由于没有进行梁体焊接，故不考虑梁段拼装误差Δ3，i， 在理论无应力线形基础上仅考虑温度变形和焊缝收缩，设第1 批梁体拼装数量为N1，其理论拼装线形也用ΦiA，1表示：

3.2 第i（i≥2）批梁体拼装

设前i-1（i≥2）批已拼装S 个梁体，第i-1 批拼装Ni-1个梁段，准备拼装第i 批梁体（拼Ni个梁段）。由于施工误差、温度变形和焊缝收缩等因素使得拼装出来的梁体线形和理论无应力线形不可避免地存在误差，故需测量各个控制点的实际坐标，以求得实际线形和理论线形的误差。 在第i-1 批梁段拼装后，对第i-1 批梁段各个控制点测量得到各个控制点的实测坐标值为：ΦiR，0=[xiR，0yiR，0]T（i=S-Ni-1+1，SNi-1+2，…，S+Ni-1+1）。 测量得到此时控制段控制点A、B 的 坐 标 值：ΦAR，0=[xiR，0yAR，0]T，ΦBR，0=[xBR，0yBR，0]T，由式（10）计算得控制段的B 控制点理论坐标与实际坐标的误差为：

后续梁体的拼装不仅要考虑已拼梁体拼装产生的误差，还要考虑后续梁段拼装过程中可能产生的温度变形和焊缝收缩，应尽量使实际拼装线形最大限度地与理论无应力线形接近。 考虑误差修正时（预留与误差相反的校正量），若直接将前面梁段拼装时所造成的误差和预测后续梁段拼装可能产生的温度变形和焊缝收缩产生的误差，全部弥补在后续拼装的第1 个梁段，可能会导致梁段之间产生较大的折角，使得梁段之间线形不平顺，对结构造成危害。 因此，前面拼装造成的误差应在后续梁段的拼装时逐步弥补，缓慢过渡。

当后续梁段误差考虑前面梁段拼装时所造成的误差和预测后续梁段拼装可能产生的温度变形和焊缝收缩时，有关系式：

在焊完、顶推前这一工况可计算焊后拼装线形（后续梁段各控制点的拼装数据）：

第i-1 批梁段拼装完毕后，进行梁体顶推（刚体平移和刚体转动），已拼装完的梁体经过顶推，线形会发生变化，但依旧有梁段放置于拼装平台上，以便与后续梁段的拼装，此时位于平台上的梁段（包括控制段）依然处于无应力状态，后续梁段的拼装也是处于无应力状态下进行拼装，故顶推后的拼装线形可以看作是焊后拼装线形经过顶推得到， 且是绕着控制段控制点A 进行的刚体转动，转角为θ，如图5 所示。

图5 梁体刚体转动示意

顶推前， 测量得到控制段控制点A、B 的坐标值：ΦAR，0=[xAR，0yAR，0]T，ΦBR，0=[xBR，0yBR，0]T，由A、B 的坐标值可计算得到顶推前控制段与水平线的夹角：

顶推后， 测量得到控制段控制点A、B 的坐标值：ΦAR，1=[xAR，1yAR，1]T，ΦBR，1=[xBR，1yBR，1]T，由A、B的坐标值可计算得到顶推后控制段与水平线的夹角：

控制段经过顶推后发生刚体转动的转角：

因此，焊后拼装线形经过顶推（刚体平移和刚体转动）得到顶推后拼装线形，又因在顶推施工过程中一直以控制点1 为坐标原点，故根据式（3）～（5）有：

4 工程应用

4.1 工程概况

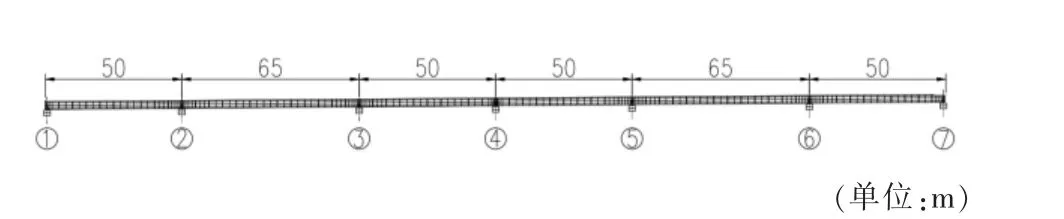
某在建钢混组合梁桥钢主梁沿桥纵向共分为30 个节段，分5 轮进行拼装顶推，每轮最多一次性拼装7 节梁段，最少拼装5 节梁段。 该桥跨径布置如图6 所示。

4.2 梁段拼装线形

图6 某桥跨径布置示意

4.2.1 顶推方案

钢梁顶推施工共分5 次拼装顶推，第一轮拼装6节梁段（A01～A06）后顶推至导梁上2#墩；第二轮拼装6 节梁段（A07～A12）后顶推至导梁上3#墩；第三轮拼装6 节梁段（A13～A18）后顶推至导梁上4#墩；第四轮拼装5 节梁段（A19～A23）后顶推至导梁上5# 墩；第五轮拼装7 节梁段（A24～A30）后，继续顶推，当导梁上6#墩时开始拆卸导梁，并继续顶推至钢主梁上7#墩。每轮梁段拼装前需计算出各梁段控制点的拼装坐标，根据坐标调整每个梁段在拼装平台上的位置。

4.2.2 梁段拼装

限于篇幅， 本文仅以第2 批次的拼装线形计算为例，说明本文拼装线形的计算过程，其余批次的拼装计算可参照处理。 前一批（第1 批）梁体拼装完成后，测量已拼梁段控制点，由式（8）计算拼装误差。 以控制点2 为例进行计算，其余控制点类似处理。 控制点2 属于桥梁第1 跨，拼装误差为相对于支座位置P1实际相对高程和理论相对高程的差值，测得实际坐标为，因此可以计算得到控制点2 的拼装误差：Δ3，2=[0.000 0.012]T， 如图7所示。 前一批其余控制点拼装误差计算结果见表1。

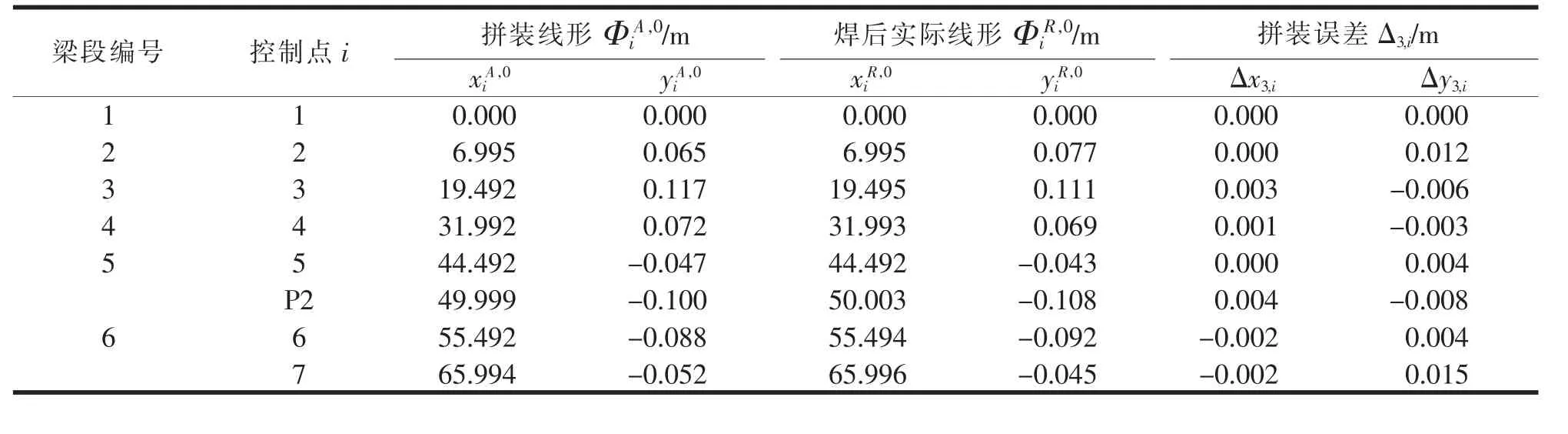
表1 第1 批梁体拼装误差计算结果

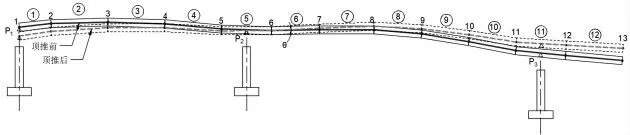
图7 第2 批梁体顶推前、后旋转示意

控制段控制点A、B 即为梁段6 控制点6、7，此时Δ3，B=Δ3，7=[-0.002 0.015]T。 第2 批梁体拼6 节梁段（梁段A07～A12），后续梁段拼装需考虑前一批梁段的拼装误差，故总误差满足式（11），后续梁段拼装坐标满足式（12），以控制点8 为例进行说明，其余类似处理。实测计算参数ΔT、 μ、ω0、梁段7 长度L7、夹角α7分别为36℃、1.2×10-5、2 mm、12 m、0.199°，根据式（11）计算得到：Δ=[0.007 0.003]T。 进一步由式（9）即可计算第2 批次梁体的拼装线形，控制点8 的理论坐标， 其拼装坐标计算如下：。

通过顶推前后控制段与水平线夹角的变化值计算出控制段发生的转角θ=1.86°（图7）， 然后根据式（16）可以得到顶推后控制点8 的拼装坐标为Φ8A,1=TΦ8A,0+U=[77.950 2.467]T。

以此类推，可计算出第2 批次梁体拼装线形的其余各控制点的误差和拼装坐标，计算结果见表2。

表2 第2 批梁段控制点拼装坐标计算结果

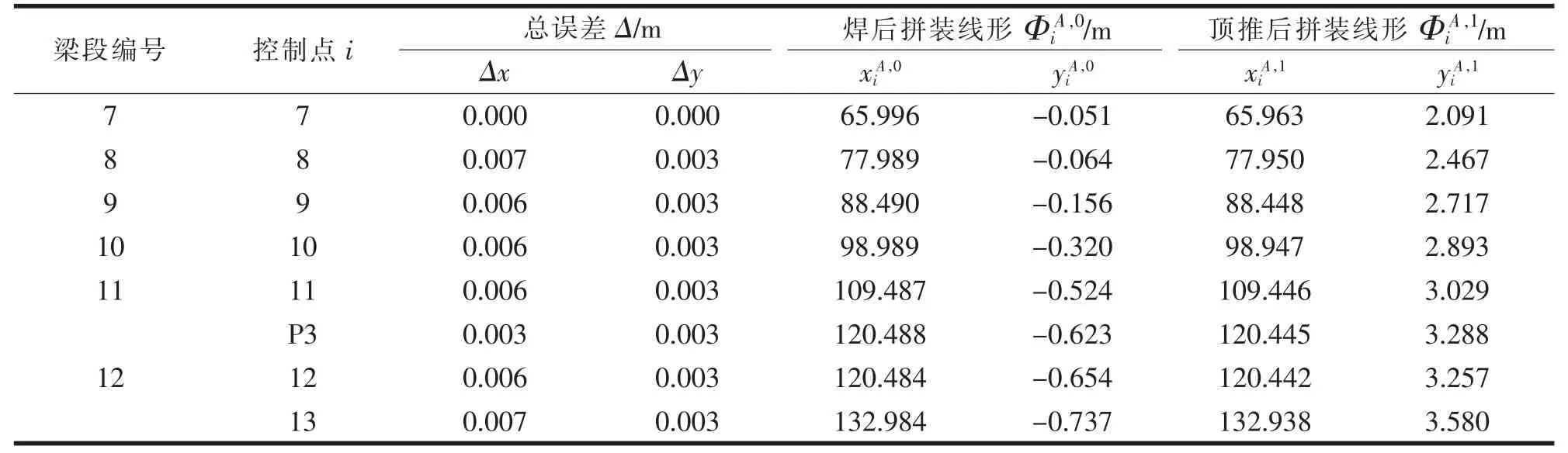
梁段编号 控制点i 总误差Δ/m 顶推后拼装线形ΦiA，1/m焊后拼装线形ΦiA，0/m Δx Δy xiA，0 yiA，0 xiA，1 yiA，1 7 7 0.000 0.000 65.996 -0.051 65.963 2.091 0.007 0.003 77.989 -0.064 77.950 2.467 9 9 0.006 0.003 88.490 -0.156 88.448 2.717 8 8 10 10 0.006 0.003 98.989 -0.320 98.947 2.893 11 11 0.006 0.003 109.487 -0.524 109.446 3.029 P3 0.003 0.003 120.488 -0.623 120.445 3.288 12 12 0.006 0.003 120.484 -0.654 120.442 3.257 13 0.007 0.003 132.984 -0.737 132.938 3.580

4.2.3 控制效果评估

全部梁段拼装顶推且落梁到设计位置后，测量各个梁段控制点，得到实测线形数据与理论顶推到位的线形（在理论无应力线形上考虑自重产生的挠度）的差值。从图8 可知，共测量35 个控制点，有32个（91.4%）控制点拼装误差在10 mm 以内，3 个控制点拼装误差超出10 mm，梁体支座位置控制点误差小于10 mm， 但最大拼装误差不超过15 mm，说明本文介绍的考虑拼装误差的钢梁顶推施工线形计算方法有效可靠，可以高精度地控制线形。

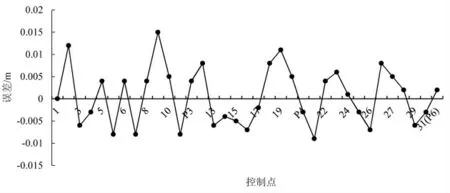
图8 实际线形误差

5 结论

本文提出一种考虑支座位置的拼装误差计算方法并采用传递矩阵法进行误差的传递与修正，最终达到对钢主梁线形精确控制的目的。 以某在建钢混组合梁桥为背景， 采用该方法控制梁段的拼装，并对控制结果进行评估。 结果表明，梁段控制点误差基本小于10 mm，梁体支座位置控制点误差小于10 mm，线形精度远超规范要求，可以高精度地控制线形，具有较高的实际工程应用价值。