基于改进Kriging 模型的大跨度斜拉桥结构可靠度分析

■王伟慷

（长沙理工大学土木工程学院，长沙 410004）

随着桥梁工程与科学技术的飞速发展，斜拉桥凭借其外形优美、受力良好、成本合理等特点得到了设计师们的青睐，被广泛地运用到大跨度桥梁中。而在施工与运营使用过程中，斜拉桥的安全性能受到拉索受损、混凝土碳化、超载以及其他各种不确定因素的影响而导致安全储备降低[1]，因此对斜拉桥结构可靠度分析有助于降低斜拉桥结构失效的风险，为其安全运营使用提供保障。

工程结构可靠度分析发展至今已经有了一系列成熟的方法，目前一次二阶矩法与二次二阶矩法仍是应用最为广泛的可靠度分析方法。 Hasofer 等[2]对多元问题中二阶矩可靠性的意义进行了基本分析，提出了一种改进的一次二阶矩法，但该方法局限于非线性较小的极限状态方程。 范文亮等[3]结合坐标旋转、单变量降维近似和非中心卡方分布提出了一种改进一阶矩和二阶矩可靠度的方法，并通过实例验证了该方法能有效提高精度和效率。 上述方法仅对显示功能函数可靠度计算有效，而实际工程中结构复杂，功能函数多是复杂的非线性隐式表达式，求解难度很大，并不适用。 随着计算机技术的发展，研究人员发现可通过采用代理模型对结构进行可靠度分析，从而减少计算成本与提高精度。 Bai等[4]将响应面技术与凸模型方法相结合，提出了一种解决非线性极限状态函数的结构可靠性分析方法，并通过实例验证了该方法的有效性。 马超等[5]通过优化算法得到支持向量机回归的可靠度指标，并将该方法应用到实际飞机机翼可靠性分析中。 潘林锋等[6]通过Kriging 模型拟合回归极限状态方程，引入HL-RF 修正算法，提出了一种新的可靠度计算方法，并通过算例验证了该方法的可行性。 李正良等[7]采用Kriging 模型对直立锁缝屋面系统进行抗风可靠度计算得到了可靠度指标。Zhang 等[8]提出了一种基于Kriging 近似的确定性数值模型的一阶可靠性分析方法，并用于岩土可靠性分析。 刘瞻等[9]将人工蜂群算法应用到Kriging 模型中，通过对模型参数寻优，计算效率和精度得到了较大提高。 但研究也发现，Kriging 模型对初始值的选择敏感，不同的初始值可能会导致不同的结果，可能会出现由于初始值的设置偏差而造成模型建立时预测结果陷入局部最优的情况，并且Kriging 模型采用模式搜索法进行单点搜索，搜索路径单一。 基于此，本文引入改进粒子群算法（IPSO）对Kriging 模型相关参数进行寻优，提出一种改进Kriging 模型的可靠度计算方法，并以某大跨度双塔斜拉桥为例，验证了该方法的有效性，以期为大跨度斜拉桥可靠度计算提供参考。

1 工程概况

某大跨度双塔斜拉桥设计等级为公路-I 级，采用双塔双索面对称式结构分布，主跨跨径为450 m，桥梁跨境组合布置为（182+450+182）m，主梁为Q345qD钢箱梁，桥塔采用C50 混凝土。桥型布置如图1 所示。

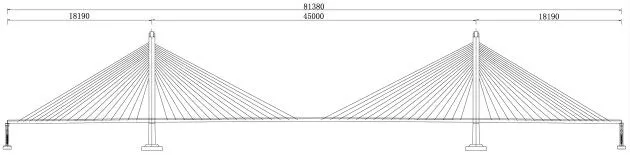
图1 双塔斜拉桥桥型布置

采用有限元软件建立桥梁有限元数值仿真模型，其中桥塔采用实体单元进行建模，主梁使用beam单元进行建模， 斜拉索使用link 单元进行建模，桥塔和桥台底部使用固结约束，斜拉桥有限元模型如图2 所示。

图2 双塔斜拉桥有限元模型

2 Kriging - IPSO 模型

2.1 Kriging 模型基本理论

Kriging 模型是一种通过将非参数随机过程与参数线形回归模型叠加而形成的插值模型，其表达式为：

式（1）中：Γ（p，x）为多项式回归向量；β 是回归系数向量，β=[β1， …，βp]；fT是变量x 的多项式，fT=[f1（x），f2（x）…， fp（x）]T；z（x）是一个随机过程，相关性用协方差表示为：

式（2）中：R（xi，xj；θ）是xi和xj之间的相关函数，相关函数模型采用高斯模型：

式（3）中：θ 是参数向量，θ=[θ1，θ2，…，θm]T；m 与M分别为第m 个维数元素和总维数。定义相关矩阵R[（xi，xj；θ）]N0×N0，如此便得到β 与σ2估值为：

式（4）、（5）中：F 表示为由训练样本点数量组成的单位矩阵。 由上述式子可知Kriging 模型可以通过β、σ2以及θ 定义。而回归系数向量以及方差则可以通过θ 得到。 故在建立Kriging 模型时，应首先由采样点获得参数向量，该过程可以通过极大似然估计来实现：

预测值y（x）的均值和方差用预测点x 表示为：

式（7）、（8）中：r（x）=[R（x，x1；），R（x，x2；），…，R（x，xN0；）]，μ（x）=FTR-1r（x）-f（x）与为（x）为x 点的预测值。

2.2 改进的粒子群算法原理

粒子群算法是一种基于鸟类捕食仿生原理的智能优化算法，通过对问题的数学描述，可以实现待优化问题的智能迭代寻优，其基本原理如下：假设待寻解空间中存在仅拥有速度与质量两种属性的粒子Q={x，v}，表示为xi=（xi1，xi2，…，xid），vi=（vi1，vi2，…，vid），分别代表了求解空间中第i 个粒子在第d 维度的位置与速度指标， 定义其在每一次迭代中的位置与速度更新方式如式（9）所示。

式（10）中：ωmin、ωmax分别为惯性权重的最小与最大值；t、tmax分别为当前进化轮次和最大进化轮次。

模型参数优化流程如图3 所示，具体步骤如下：（1）初始化算法参数。 设置算法最大迭代次数，设置惯性权重的最大与最小值，设置学习因子取值，设置算法维度。（2）初始化粒子群。采用随机初始化的方式初始化粒子群在搜索空间中的位置，形成初始粒子种群。 （3）计算适应度值。 （4）粒子位置与速度更新。 根据式（10）计算基于迭代轮次的非线性递减惯性权重值，再根据式（9）粒子速度与位置更新公式更新粒子群在搜索空间中的位置。 （5）计算适应度并筛选最优个体。 计算粒子群的适应度值，筛选出个体最优和种群历史最优，判断算法是否达到最大迭代次数，若达到则算法终止，若未达到则返回步骤四“粒子位置与速度更新”。

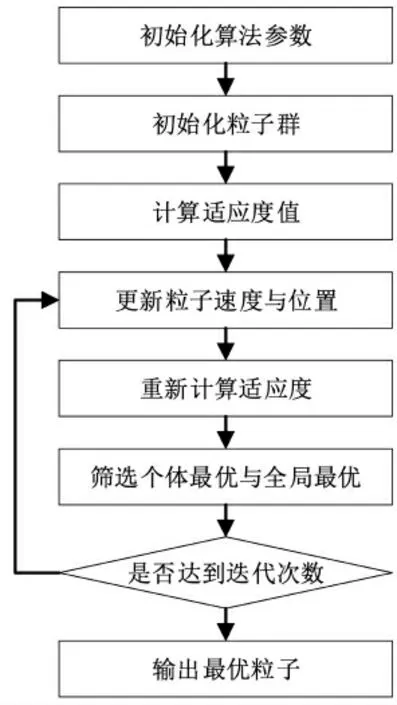
图3 粒子群算法执行流程

2.3 Kriging-IPSO 计算模型的建立

基于有限元模型和MATLAB 计算程序，提出了Kriging-IPSO 混合响应面法，对结构的可靠性进行计算和分析。 处理过程如下：（1）确定桥架结构在使用运行过程中随机变量的统计特征和概率分布，并采用均匀设计方法生成输入样本点；（2）根据桥的设计数据和运行条件，在通用有限元软件中完成建模，计算得到输出样本，然后用输入的样本形成一个训练样本；（3）规范化样本点，建立基本Kriging模型，通过对基本模型输入采样点无监督的训练和参数优化得到结构Kriging 模型；（4）随机变量的归一化，通过惩罚函数将约束优化问题转化为无约束优化问题，然后再建立一个适合IPSO 算法计算的精确度方程；此外，IPSO 算法更新了搜索粒子和粒子群的最优位置，迭代获得随机变量的最优权值，以支持克里格模型的无监督学习过程；（5）通过克里格模型的预测结果，建立了求解结构可靠性指标的数学模型。

3 大跨度斜拉桥可靠度分析

3.1 斜拉桥随机变量的统计特征

本文根据工程概况介绍的实际工程进行分析，在桥梁施工与运营过程中，由于桥梁自身材料以及外部荷载等参数的变化存在不确定性，导致桥梁的实际设计状态往往不能达到理论设计状态。 而影响斜拉桥的结构安全的因素有许多，本文仅以结构的几何变形为控制指标对斜拉桥进行可靠性分析，选取随机变量（表1），各参数的选取根据GB50153-2008《公路工程结构可靠度设计统一标准》和参考文献[10]得到。

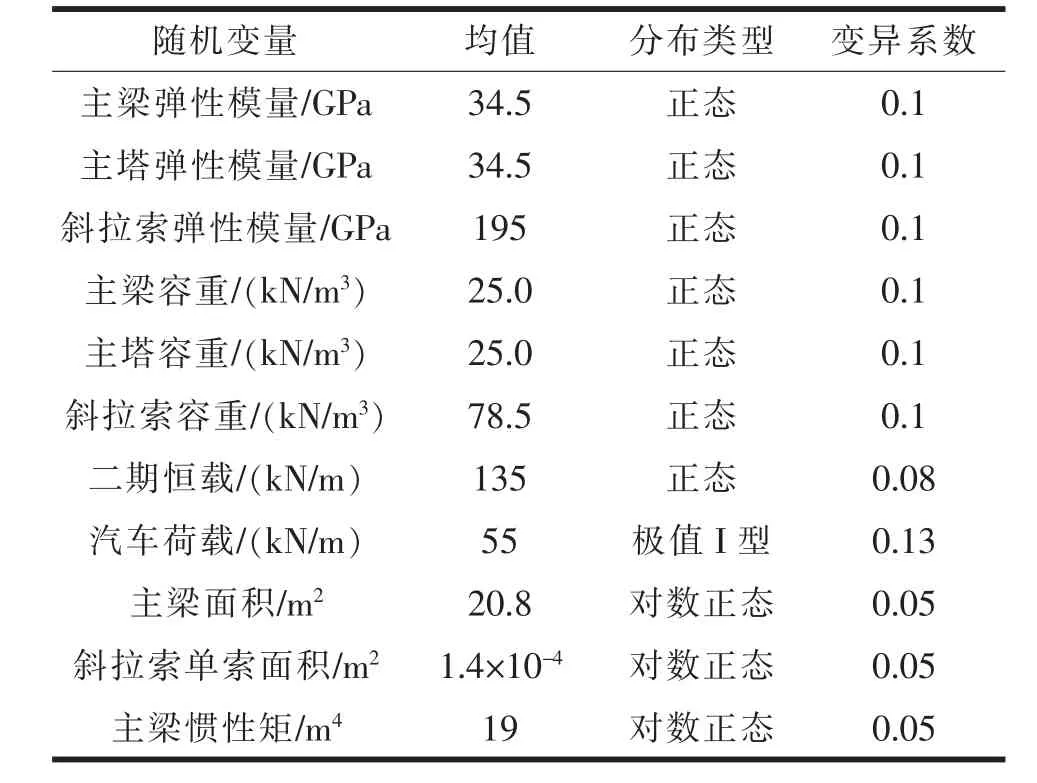
表1 随机变量参数统计

3.2 极限状态方程

由JTG/TD65-01-2007《公路斜拉桥设计细则》规定斜拉桥主梁在车辆荷载作用下（不包括冲击力）最大允许变形为：

由式（11）可以得出极限状态方程：

3.3 可靠度指标求解

将选取的各个随机变量作标准正态化处理，便能得到标准正态分布变量Z1，Z2，…，Z11，故式（12）可以表示为y（Z1，Z2，…，Zn）=0，得到可靠指标的计算公式为：

式（13）中：（Z）=0 表示约束条件。 采用罚函数法对上式进行处理，将约束优化问题转化为无约束优化问题，也就是求极值问题，得到方程：

本文采用均匀设计抽样方法，在[μ-3σ，μ+3σ]范围内生成50 组随机样本，然后采用内插法得到训练样本如表2 所示（仅列出前3 项）。

表2 训练样本示例

根据斜拉桥的有限元模型，将上述训练样本值依次输入模型进行计算， 得到50 组随机变量样本下的跨中变形。 将计算得到的变形数据代入式（12）， 最后生成主梁随机参数缺陷的训练样本，将样本点归一化， 得到输出样本数据如表3 所示，转入Kriging 模型中进行训练。 为验证IPSO 算法对Kriging 模型参数寻优的效率， 采用PSO 算法对同一样本数据进行处理，对比结果如图4 所示。 可以看出IPSO 算法在对Kriging 模型参数寻优过程中适应度曲线进化速率远高于PSO 算法，且50 轮迭代结束后，IPSO 算法的种群最优值明显优于PSO算法。 IPSO 算法最终优化模型参数结果如图5 所示。 可以得到，IPAO 算法优化的最小均方差误差为0.000 252，足以保证高精度响应面的构建。

表3 归一化后的输出样本

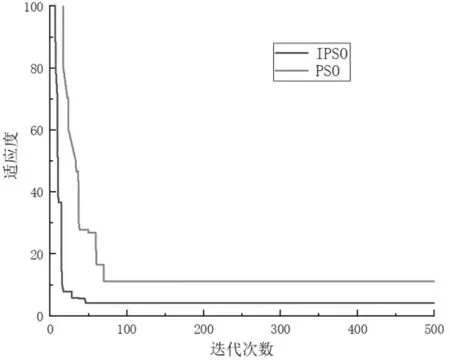
图4 寻优结果对比

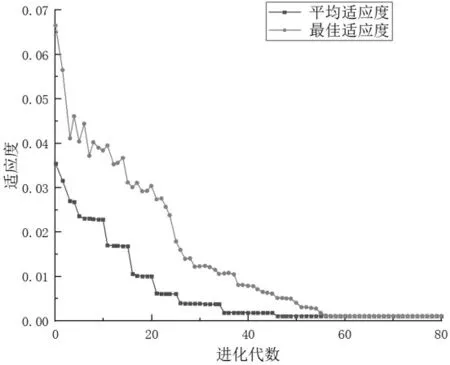
图5 优化模型参数结果

基于Kriging 模型， 使用训练样本进行回归预测，预测结果如图6 所示。 可以看出Kriging 模型可以真实地模拟斜拉桥主梁的结构极限状态函数，并且具有很高的精度。

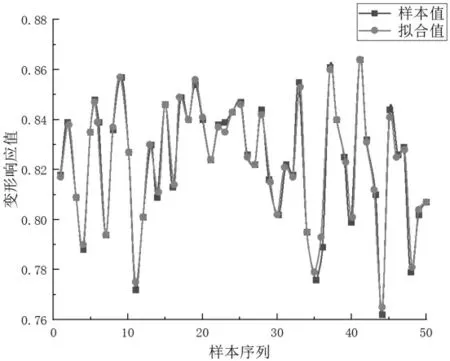
图6 样本值与拟合值比较

采用本文改进的粒子群算法对式（14）进行求解，迭代过程如图7 所示。 可以看出，本文改进的粒子群算法在对斜拉桥可靠性计算过程中进行了46 次迭代就达到了收敛，得到对应的可靠性指标β 为4.212 5。 为验证本文计算方法的准确性，采用蒙特卡洛法对同一样本数据进行抽样模拟，得到可靠度指标为：4.211 8，与本文结果误差值为0.000 7，相对误差为0.016 7%，验证了本文计算方法的精确度。

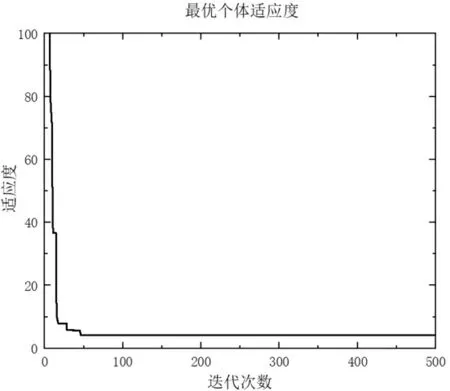
图7 改进粒子群算法迭代过程

4 结论

在对复杂的大跨度斜拉桥进行可靠性分析时，由于目标函数往往呈现高维非线性，并且没有明确的解析表达式， 从而导致计算精度低与不容易收敛， 本文提出一种基于Kriging 模型和改进粒子群算法的Kriging-IPSO 混合算法来求解斜拉桥的结构可靠性。 通过对实际工程的计算，结果表明，该方法在样本数量、计算精度和效率方面有较大的优势，可以与现有有限元软件相结合分析斜拉桥结构可靠性，主要结论如下：（1）该算法将Kriging 模型与改进的粒子群算法（IPSO）相结合，利用Kriging模型建立一个小样本、非线性、高维的隐式功能函数响应面模型，结合IPSO 算法，改进了传统PSO 算法收敛速度慢与不成熟问题；（2）实际斜拉桥结构分析，结果表明，提出的改进Kriging-IPSO 模型提高了计算精度与计算效率，克服了传统的响应面法对高非线性结构可靠性分析的局限性；（3）与传统的桥梁可靠性分析方法比较，该方法具有样本数量小、计算精度高、易于通用有限元软件相结合的优点，方便实际工程应用，可为斜拉桥可靠性计算的研究提供新的思路。