基于Bayesian最小误判的活动轮廓模型

党红宇, 唐利明, 徐雅雅

(湖北民族大学 数学与统计学院, 湖北 恩施 445000)

0 引言

图像分割[1-2]是许多图像处理和计算机视觉中的基本任务,它旨在将图像转换为具有指定标签的像素区域的集合,并且可以对标记的目标进行定位和区分.图像分割结果的优劣直接影响后续的分析,但是由于噪声、背景信息干扰等现象的出现,使得图像分割变得越来越复杂.因此在图像分割中如何抑制噪声和背景的干扰,提高分割精度成为主要研究内容.

在统计学和图像分割领域,高斯分布是一种广泛应用的概率分布模型,其在描述及建模自然现象和图像数据中具有重要作用.在此基础上,变分水平集活动轮廓图像分割方法[1-4]基于Bayesian最大后验估计来构造相关能量泛函,在图像分割中表现出良好的性能.很多学者在对图像的目标和背景分割研究时,融入一些统计先验信息对图像进行建模[5-6],通常假设目标和背景分别服从不同参数的高斯分布.2001年,Chan等[7]提出了著名的无边缘活动轮廓模型(CV),假设目标和背景分别服从两个不同均值的高斯分布,结合最大后验概率理论,从全局角度构建能量泛函.CV模型对目标和背景内部分布均匀、类间对比度较大的图像具有良好的效果,但由于它是全局模型对灰度不均图像分割结果不理想.

为分割灰度不均图像,Li等[8]提出了基于区域的局部二值拟合模型(LBF).该模型假设在各个局部区域中图像灰度服从不同均值的高斯分布,所以它是一个局部模型,可以很好地处理灰度不均.但LBF模型仍只利用均值特征来描述图像的灰度分布,没有考虑方差特征,对于一些严重退化图像仍不能取得很好的实验结果.于是Wang等[9]提出了局部高斯拟合模型(LGDF),严格依据变分原理及最大后验理论推导得出局部灰度均值和方差,并进行了详细的统计解释,但是当图像受到不同噪声的影响时,该模型很难很好地分割图像.为了在增强模型抗噪声能力的同时保持对灰度不均匀性的鲁棒性,Li等[10]提出一种基于Bayesian理论的局部活动轮廓模型,该模型不仅假设图像灰度在每个局部区域的条件概率满足不同均值和方差的高斯分布,还引入一种基于马尔可夫随机场的连通映射空间正则化作为先验概率,提高了模型对噪声的鲁棒性.

上述模型可以较好地分割灰度不均图像,但是并不能进行灰度不均图像的矫正.为解决此问题,Li等[11]进一步将局部灰度的均值特征近似为局部邻域内变化缓慢的偏移场与一个相关常数的乘积,提出了一种局部灰度聚类模型(LIC),将该模型用于磁共振图像偏移场校正与分割,取得了较好的效果,但并未考虑图像的局部灰度方差,可能导致分割不准确.因此Zhang等[12]提出了基于变换域中的极大似然准则变分模型(MLTD),该模型将原始图像灰度映射到变换域中,结合极大似然判决定义了基于局部区域不同均值、偏移场和方差的能量泛函,最小化灰度重叠和判决错误像素点的概率,更好地分离两个区域的高斯分布.此后提出的LSACM模型[13](locally statistical active contour model, LSACM)也具有相似的思想.上述模型对简单图像,包括灰度不均图像都能取得较好效果,但是对于含有纹理、丰富细节或者噪声的图像,不能得到准确的分割结果.因为纹理、细节和噪声会使得目标和背景的分布产生混叠现象,从而使得目标和背景不容易被区分开来,而产生误分割.

为解决此问题,本文提出了一种基于Bayesian最小误判的活动轮廓模型.首先,通过扩散方程在切线方向的扩散,降低噪声、纹理等高频信息的变化,得到原图像的一个平滑近似图像.依据基于类间马氏距离的最小误判概率准则,与原图像相比,平滑近似图像对应的目标和背景这两个类别之间的马氏距离增大,误判概率减小,提高了分割精度.然后结合迭代卷积阈值框架下的局部二值拟合活动轮廓模型,对特征函数进行迭代演化,直至收敛到目标边缘.最后采用结合梯度下降法及迭代卷积阈值化方法对模型进行数值求解.实验结果表明,本文模型可以很好地抑制噪声等干扰信息,准确提取目标轮廓,误判概率更小.与5个经典的变分图像分割模型相比,本文模型展示出较好的实验效果.

1 基于Bayesian最小误判的活动轮廓模型

1.1 基于Bayesian最小误判的图像分割

图像分割就是将图像的特征空间Ω划分为两个子区域Ω1和Ω2,即分别为图像目标和背景区域,满足Ω1∪Ω2=Ω,Ω1∩Ω2=∅.当x∈Ω1时,判x∈ω1目标类;当x∈Ω2时,判x∈ω2背景类.依据Bayesian统计判决的基本方法,这时可能会发生两种错误,一种是把实属ω1类的像素点判属ω2类,发生这种错误的原因是属于ω1类的像素点在特征空间中散布到Ω2中去,从而将其判为属于ω2类;类似地,另一种错误是把实属ω2类的像素点判属ω1类,如图1所示,t*是最佳门限,显然它比任一门限t的误判概率要小.设ω1和ω2类出现的概率分别为P(ω1)和P(ω2),则总的误判概率可表示为:

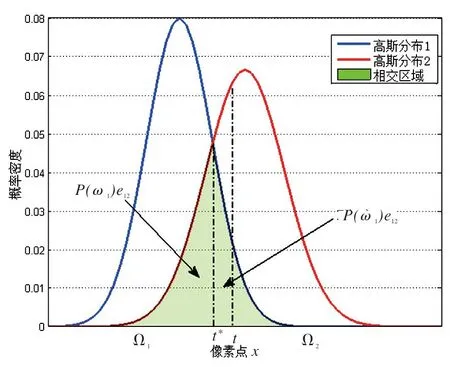
图1 两类高斯分布误判概率示意图

(1)

从而得到最小误判概率准则下的判决规则(似然比形式):

(2)

这里l12称为似然比,P(ω2)/P(ω1)称为似然比阈值,通常记为θ12.因此在统计意义下,如何降低误判概率,得到更准确的判决结果是我们需要考虑的问题.

1.2 Bayesian图像分割的误判度量

本节讨论Bayesian最小误判准则的图像分割的误判度量.假设目标和背景分别服从如下两个高斯分布:

(3)

其中p(x|ωi)表示属于ωi类的n维模式x的多变量高斯分布密度函数:

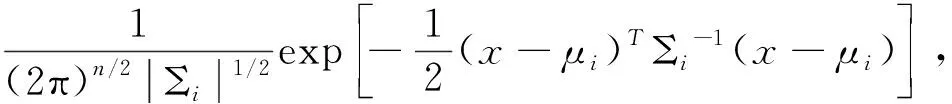
式中,μi=Ei(x)为ωi类模式的均值矢量,Σi=Ei[(x-μi)(x-μi)T]为ωi类模式的协方差矩阵,|Σi|表示Σi的行列式.为了简化计算,我们讨论一种特殊情况,Σ1=Σ2.根据判决规则的似然比形式,则对数似然比为:

(4)

由上式可知L12(x)是x的线性函数,因x的各分量是服从高斯分布的,故L12(x)是高斯分布的随机变量.由式(4)可得L12(x)在x∈ω1条件下的数学期望:

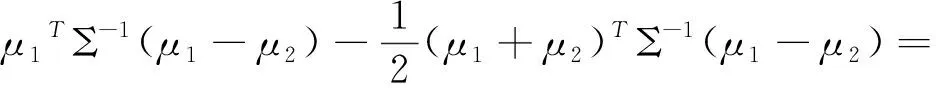
(5)

令r122=(μ1-μ2)TΣ-1(μ1-μ2),显然,r12为这两类中心的马氏距离,于是有

L12(x)在x∈ω1条件下的方差:

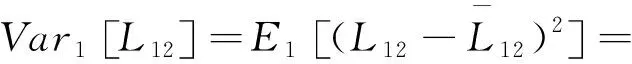
(6)

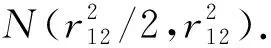
设α=lnθ12=ln[P(ω2)/P(ω1)],由判决规则可知,将属于ω1类的像素点误判为属于ω2类的错误概率为P(L12<α|ω1),而将属于ω2类的像素点误判为属于ω1类的错误概率为P(L12>α|ω2),具体计算如下:

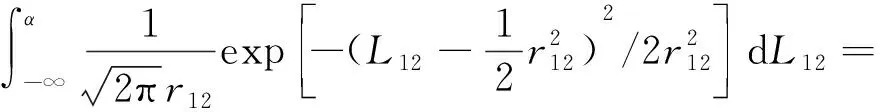
(7)

(8)

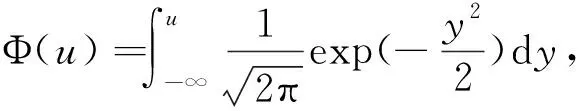
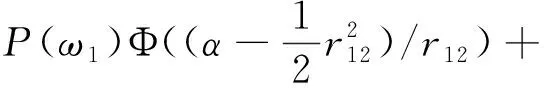
(9)

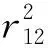
(10)

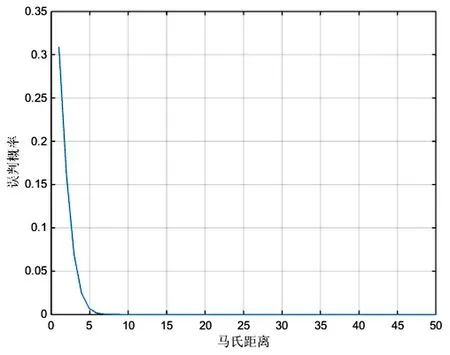
图2 误判概率随马氏距离的变化

特殊地,对于灰度单通道图像I:x∈Ω→R,本文定义目标和背景两个类别分别服从如下高斯分布:

上式中,μ1,μ2为目标和背景的灰度均值,σ2为目标和背景的灰度方差.于是本文将目标和背景两类之间的马氏距离定义为:

(11)

对于多通道图像I:x∈Ω→R3,例如彩色图像,R3表示彩色图像R,G,B三个通道的强度.通常假设目标和背景两个类别分别服从如下三维高斯分布:

上式中,μ1,μ2为目标和背景的灰度均值向量,Σ为目标和背景的灰度协方差矩阵.于是本文将目标和背景两类之间的马氏距离定义为:

(12)

下面我们考虑如何增大马氏距离,使目标和背景两个类别在特征空间中更加分离,使得误判概率减小,得到更准确地分割结果.

1.3 增大目标和背景马氏距离的方向扩散

在图像分割任务中,纹理、噪声等干扰信息通常由快速变化的灰度值造成,会影响分割过程.根据马氏距离和最小误判概率之间的关系,我们首先进行了一个预处理步骤,通过减少图像中的噪声、去除不必要的细节并平滑图像,使区域内部像素值更加接近,不同区域之间的像素差异增大.这样马氏距离随之变大,使得误判概率最小,能更准确地提取目标.基于上述解释,我们利用如下方向扩散方程:

(13)

与原图像相比,扩散后得到的平滑近似解分段光滑,目标和背景的均值差变化微小,而灰度方差σ2大幅减小.结合式(11)可知,马氏距离随之增大,从而使得误判概率减小,目标和背景两个类别在特征空间中更加分离.如图3所示,我们以两幅纹理图像为例,第1行展示了图像扩散前后的某一截面的灰度分布图,可以发现震荡剧烈的部分在扩散后变得更加平滑,目标和背景之间的区分度更大.第2行为最终分割结果以及原图像的直方图,第3行为扩散后得到的平滑近似解的可视化图以及对应直方图.从视觉效果上看,平滑近似解中纹理、噪声等干扰信息模糊并减弱;通过对比直方图,扩散后灰度方差σ2减小,即两个高斯分布曲线宽度更小,目标和背景的灰度重叠部分明显减少,从而目标和背景更加分离.

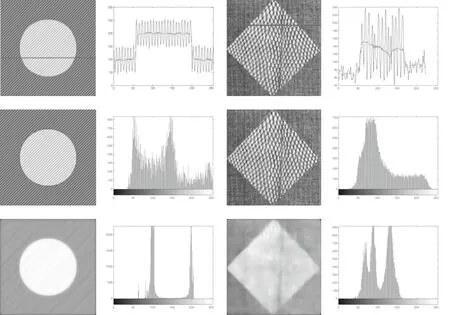
图3 本文模型对2幅纹理图像的分割结果及灰度值分布

同时,我们计算了扩散前后两个类别之间的马氏距离.如图4所示,扩散后得到的平滑近似解马氏距离更大,从而误判概率更小,分割更加容易且结果更准确.

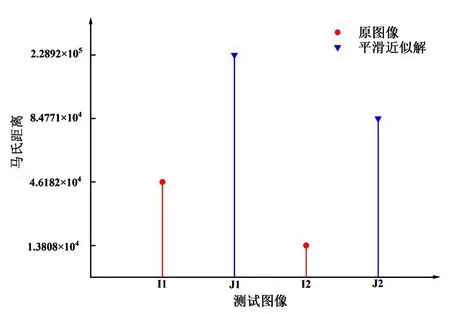
图4 图3中2幅测试图像及其平滑近似解对应的马氏距离对比

1.4 基于Bayesian最小误判的活动轮廓模型

传统结合统计先验信息的分割模型,可以较好地处理灰度不均、弱边界图像,但是对于背景信息、纹理、噪声等干扰分割过程的问题并没有得到很好的解决,即很容易将背景中部分区域判为目标(反之亦然),造成严重的误分割.针对此问题,本文将上述平滑近似解融合到局部二值拟合模型(LBF)中,构建基于Bayesian最小误判的活动轮廓模型,能量泛函定义如下:

这里Kσ(x-y)为高斯核函数,J(y)为经过前述方向扩散方程得到的原图像的平滑近似图像,fi(x)为目标或背景区域的局部灰度均值;Length(Γ)为模型长度项,μ为长度项系数;λ1,λ2>0,为非负参数,本文中设定λ1=λ2=1.

为便于求解上述活动轮廓模型,许多数值方法被提出,例如凸松弛[14]、Split Bregman[15]等.其中水平集方法(LSM)由于能较容易地处理曲线演化过程中的拓扑结构变化已被广泛应用.但是该方法需要周期性地重新初始化水平集函数,并且引入了相对较小的时间步长,限制了轮廓的演化.文献[16]提出利用分割区域的特征函数表示曲线.此后,Esedoglu等[17]提出利用热核卷积的特征函数表示周长.Wang等[18-19]和Ma等[20]使用热核卷积的特征函数代替经典变分模型中的长度项,设计了迭代卷积阈值化方法(ICTM)最小化能量泛函.表明该方法是有效的且无条件稳定的,不需要引入额外的变量和参数,计算效率更高,轮廓演化更稳定.于是本文利用特征函数表示分割区域,能量泛函转换为:

E(f1(x),f2(x),u(y))=
λ1∬ΩKσ(x-y)(J(y)-f1(x))2u(y)dydx+
λ2∬ΩKσ(x-y)(J(y)-f2(x))2(1-u(y))dydx+
μLength(Γ),

(14)

上式中u为表示分割区域的特征函数,同时利用热核卷积的特征函数表示长度项,近似写为:

则本文极小化问题如下所示:

(15)

以上为多目标优化问题,下节将采用交替迭代算法对此优化问题进行求解.

2 数值求解

本节中,我们将详细描述本文提出模型的数值求解方法的步骤和实施细节.分为方向扩散方程的数值实现以及用迭代卷积阈值化方法最小化能量泛函两部分.

2.1 方向扩散方程的数值实现

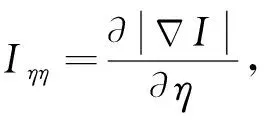
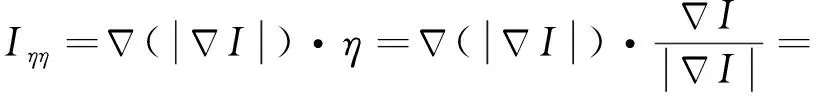
故得

(16)

结合本文提出的方向扩散方程(13),可得

(17)

利用有限差分法即可得到方向扩散方程的数值实现(见表1).

表1 方向扩散方程(13)的数值实现步骤

2.2 迭代卷积阈值化方法最小化能量泛函

在上一步得到原图像I的平滑近似图像J后,本文极小化问题如1.4节式(15)所示,主要采用交替迭代算法求解以上多目标极小化问题.对于f1(x)和f2(x)的求解,我们直接采用变分法,可得其最优的解析解(见表2).极小化问题如下所示:

表2 极小化问题(18)的数值实现步骤

(18)

对于u子问题,令

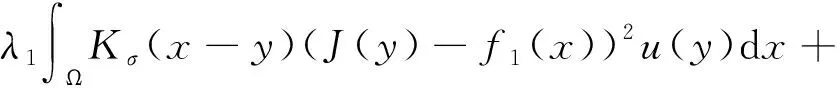
上述问题是光滑且非凸的,可利用文献[18]中线性框架去求解,于是问题(18)等价为

(19)

其中,

因为在凸集上线形函数的极小值可以在边界处获得,故

(20)

3 数值实验

为验证本文模型和算法的有效性,本文选取了被噪声干扰合成图像、含纹理细节、背景中部分灰度与目标相似的自然图像分别进行了分割实验,并与流行的5种模型进行对比实验,结合DSC、IOU、Precision以及Recall这4种评价指标测试模型的分割性能.实验环境为sys89 Intel(R) Core(TM) i3-2120 CPU @ 3.30GHz 3.30GHz matlab R2014b,自然图像来自weizmann数据库和ECSSD数据库.

3.1 评价指标

本文采用Dice相似性系数(dice simiarity coeffcient, DSC)、交并比(intersection-over-union, IOU)、精确率(precision)和召回率(recall)对分割结果进行评价.这4个指标的范围均在0到1之间,值越大(越接近于1),分割结果越好.定义如下:

其中,A,B分别为真值图和分割结果,TP表示真正例,FP表示假正例,FN表示假反例.

3.2 本文模型的有效性

首先验证模型的有效性,实验对象为3幅合成图像及3幅自然图像.实验结果如图5和图6所示,从左到右分别展示了带有初始轮廓的原始图像、原图像的灰度分布直方图、分割结果以及平滑近似图像的灰度分布直方图.从实验结果可以看出本文模型达到了预期的结果,减弱了噪声、纹理以及背景灰度与目标相似等干扰信息的影响,可以较准确地分割含上述干扰的图像.此外,图7展示了扩散前后目标和背景马氏距离对比柱状图,可见扩散后马氏距离都增大,灰度重叠部分减少,这意味着误判概率减小,更有利于分割.

图5 3幅合成图像的分割结果及扩散前后直方图对比

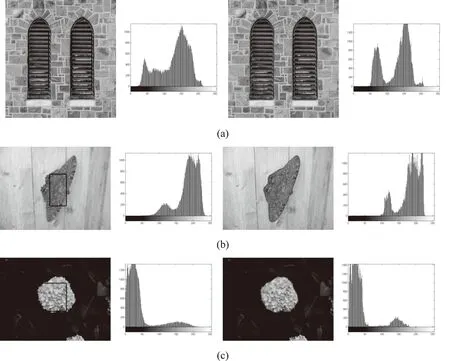
图6 3幅自然图像的分割结果及扩散前后直方图对比

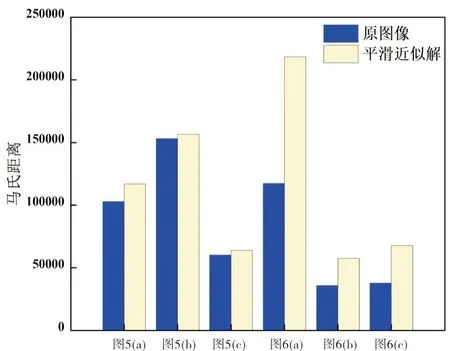
图7 图5和图6中测试图像与其平滑近似解的马氏距离对比

其次,本文验证了算法的收敛性,实验数据仍为图5和图6中的6幅图像,迭代次数统一设定为45次,并计算每一次迭代后的能量值(见式(14)).图8展示了能量值随迭代次数增加的变化图.从图中可以看出,能量随着迭代次数的增加,稳步下降最终趋于稳定.

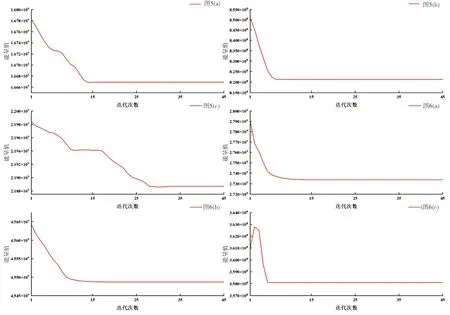
图8 图5和图6中测试图像能量值随迭代次数的变化

下面验证本文模型对噪声的鲁棒性.实验数据选择1幅合成图像,对其加不同程度不同类型的噪声进行测试(见图9).从上往下依次是添加了方差分别为0.10,0.15,0.20,0.25,0.30的高斯噪声、噪声密度分别为0.02,0.04,0.06,0.08,0.10的椒盐噪声、方差分别为0.05,0.10,0.15,0.20,0.25的光斑噪声对应的分割结果.从实验结果可以看出,本文模型可以收敛到一个相对准确的边缘,对高强度噪声具有一定的鲁棒性.

图9 本文模型对不同程度噪声的分割结果

3.3 对比实验

本节与CV[7]模型、LGDF[9]模型、LPF[21]模型、HLFRA[22]模型、ICTM_LBF[18]模型五个模型进行对比实验.实验对象均为自然图像,实验结果见图10和图11.从上往下依次为带有初始轮廓的原始图像(分别记为图10和图11)、上述五个模型的分割结果、本文模型的分割结果以及真值图.从实验结果可以看出,在这6个模型中,本文模型能更好地排除背景杂乱信息的干扰,如图10(a、c、d)等,其余5个模型基本都能捕捉到目标轮廓,但是同时也把背景中一些不相关的部分提取出来,这影响了分割的准确性.而本文模型通过扩散的预处理步骤使得目标和背景马氏距离增大,误判概率减小,得到了更为准确的分割结果.除此之外,对于含纹理细节且其与目标灰度接近的自然图像,本文模型也能较成功地提取到目标边界,如图11(a、b、d).我们选取的5个对比模型都不同程度地将图像中与目标灰度接近的细节部分分割出来,然而这并不是理想的分割结果.而本文模型可有效将可能被判定为目标的部分平滑化,较为精确的区分目标区域和背景区域,得到正确的目标轮廓.

图10 本文模型与CV、LGDF、LPF、HLFRA、ICTM_LBF模型的分割结果对比之一

图11 本文模型与CV、LGDF、LPF、HLFRA、ICTM_LBF模型的分割结果对比之二

以召回率(Recall)为横坐标,精确率(Precision)为纵坐标的P-R曲线图展示了本文模型对上述12幅测试图像分割结果的评价结果(见图12).从图12中我们可以看出,当Recall值很高时,本文模型对应的Precision值也很高,而CV模型、LGDF模型、LPF模型、HLFRA模型、ICTM_LBF模型5个模型的P-R曲线较为震荡,只有个别图像的指标值较为理想.此外,本文模型的P-R曲线在其余5个模型的上方,这说明本文模型的性能优于其余模型.

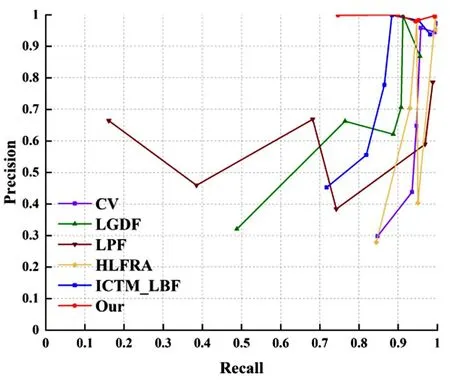
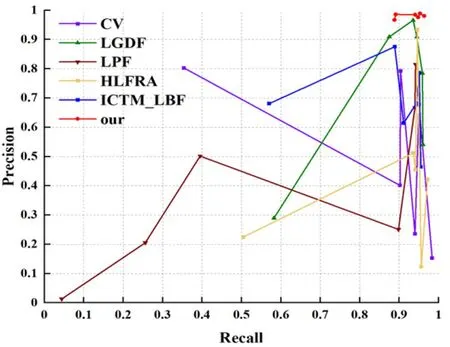
图12 本文模型与CV、LGDF、LPF、HLFRA、ICTM_LBF模型的Recall、Precision值对比

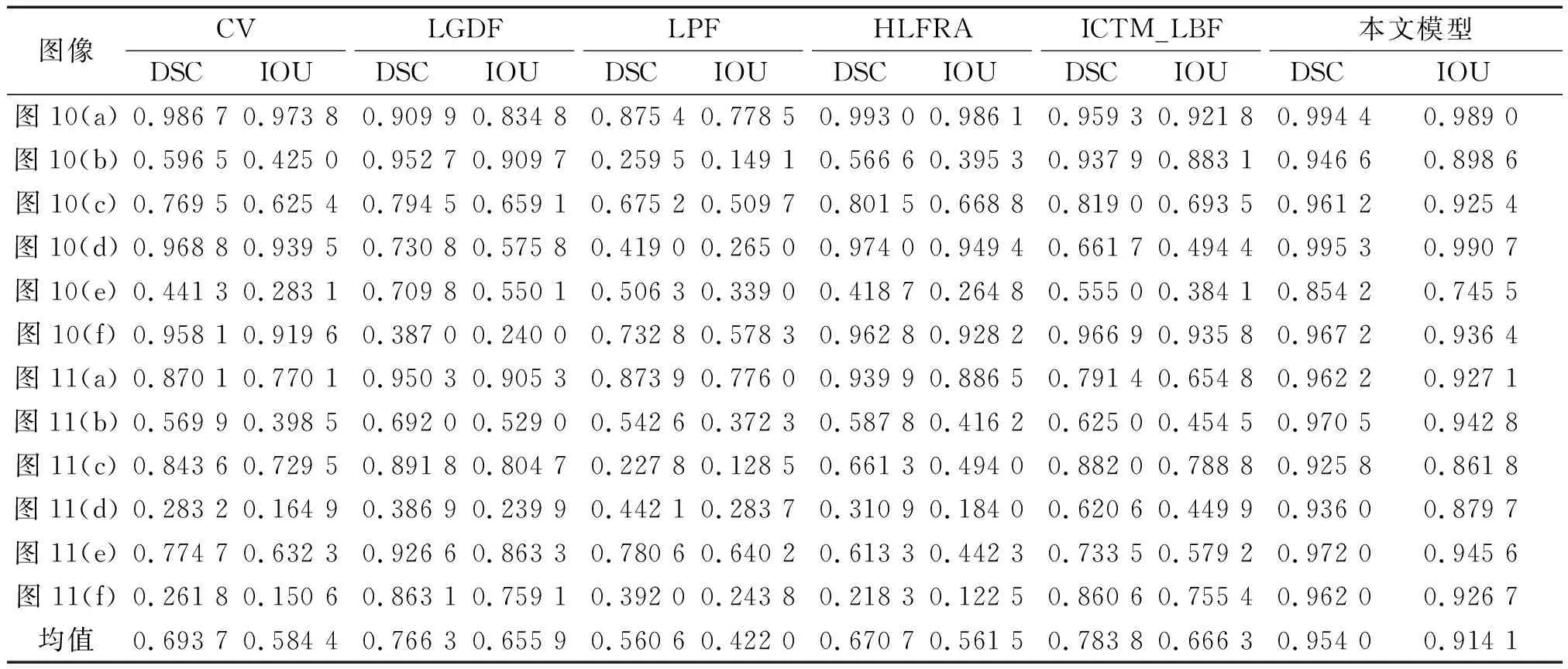
表3 本文模型与CV、LGDF、LPF、HLFRA、ICTM_LBF模型的DSC、IOU值对比

为进一步验证本文模型的分割准确性,表3展示了6个模型对12幅自然图像分割结果的DSC值和IOU值以及对应平均值.实验结果显示,CV模型、LGDF模型、LPF模型、HLFRA模型、ICTM_LBF模型5个模型对个别符合模型假设的图像DSC值和IOU值接近于1,分割结果较好,但对于自然图像,大多都受到一些背景信息、纹理等干扰,避免不了不同程度的误分.而本文模型可以较好地排除这些干扰,准确提取目标轮廓.除图像10(b)外,本文模型的分割结果具有最大的DSC值和IOU值,这进一步说明了本文模型在这6个模型中具有最优的实验效果.

4 结论

本文针对传统活动轮廓模型对含噪声、复杂背景图像分割效果不理想的问题,提出一种基于Bayesian最小误判的活动轮廓模型.首先,该模型将目标和背景这两类中心的马氏距离作为误判概率的判决规则,利用方向扩散方程使扩散只沿着切线方向发生,噪声、纹理等干扰信息被减弱和模糊,从而使目标和背景马氏距离增大,减小了误判概率,可以更精准地判决像素值属于目标或背景.然后结合迭代卷积阈值框架下的局部二值拟合模型,对特征函数进行迭代演化,直至收敛到目标边缘.最后采用结合梯度下降法和迭代卷积阈值方法对模型进行数值求解.实验结果表明,本文可以很好地排除干扰信息的影响,准确地提取目标轮廓,误判概率更小.和几个经典的变分图像分割模型相比,本文模型展示出较好的实验效果.本模型虽然所需分割迭代次数较少,但相较于几种全局模型的分割时间,在分割速度方面还需进一步提升.