基于克里金插值法的常压刀盘刀梁区域泥饼发育程度算法及应用研究
2024-05-07陶冬青郭建豪陈莉娜
杨 云, 陶冬青, 郭建豪, 陈莉娜, 兰 浩,*
(1. 湖南师范大学工程与设计学院, 湖南 长沙 410000; 2. 中铁十四局集团大盾构工程有限公司, 江苏 南京 210000)
0 引言
随着社会的发展及城市化进程的加快,越来越多的建筑拨地而起,大厦密集,城市道路四通八达,但与此同时,各种问题也接踵而至,如用地紧张、生存空间拥挤等。在这种情况下,人们开始大力开展对城市地下空间的开发。盾构法施工具有施工速度快、洞体质量较稳定、对周围建筑物影响较小等优点,被广泛应用于城市交通隧道、市政隧道的建设中。盾构法适用于软土地基段施工,在强风化岩石地层或黏土地层掘进时,被刀盘切削破碎的渣土受持续碾压作用形成半固结或固结块状体,黏附在刀盘结构上形成泥饼[1]。盾构施工过程中若遇到结泥饼难题,轻则造成转矩和推力大幅度增加、推进速度降低、刀具异常磨损,重则导致盾构土舱阻塞、掘进困难[2-3]。泥饼问题会带来很多负面影响,包括刀具被泥饼糊住,导致盾构的掘进效率急剧下降、清理刀盘费时、频繁的干预以及额外的挖掘成本[4]。
针对上述问题,很多学者就泥饼的形成机制、原因及如何改善结泥饼现象等展开了研究。如: 严辉[2]通过刀盘结泥饼案例调查,从地质、机械和施工人员因素等方面分析了刀盘结泥饼的成因,指出了当黏土粒、碎屑含量大于25%时,隧道施工工艺和刀盘结构的不利因素组合会使泥饼发生的可能性增加。胡欣雨等[5]展开了砂卵石地层土压盾构开挖面动态平衡机制研究,指出由于该地质条件下开挖土塑流性差、含水量高、渗透系数大,在土舱内易发生闭塞、结饼。王助锋等[6]以降低出现结泥饼为目标,从刀盘开口率设计、刀具布置及刀高设置等方面进行刀盘刀具针对性优化设计。邓彬等[7]、翟圣智等[8]、陈馈等[9]、刘卫[10]依托地铁盾构施工项目,分析了盾构刀盘结泥饼的机制,并提出了防止刀盘结泥饼的有效措施。Thewes等[11-12]和Zumsteg等[13-14]通过研究泡沫剂和分散剂与泥饼的相互作用机制,主张通过在渣土中添加泡沫剂和分散剂进行渣土改良防止刀盘结泥饼。
大量学者对刀盘泥饼与温度之间的相互影响关系展开了进一步研究。如: Von等[15]、Wang等[16]指出在盾构掘进过程中,旋转刀盘通过与土壤摩擦生热,导致界面温度升高。Ying等[17]指出刀盘上泥饼的存在会影响温度场,同时热量会使土壤凝固并加剧泥饼问题,导致恶性循环。因此,泥饼问题不仅是堵塞的结果,而且是摩擦热引起的渣土凝固的结果[18]。Abuel-Naga等[19]指出,土壤的黏附强度随着温度的升高而增加。已知刀盘泥饼与温度之间的相互影响关系,许多学者通过刀盘上少数测点的温度变化趋势对泥饼情况进行判断。如: Ji等[20]通过布置在刀盘上4个点位切刀中的磨损/温度传感器,建立了基于切刀温度和磨损变化规律的刀盘结泥饼诊断方法。Fu等[21]基于安装在常压刀盘中心锥背面的温度变化斜率,建立了刀盘中心区域泥饼判别方法。而Thewes等[22-23]、Feinendegen等[24]和Hollmann等[25]则通过土壤临界稠度试验研究先后提出了用于预测刀盘结泥饼及堵塞风险的经验图表,但该方法受判别人员主观因素影响大,容易出现偏差。
针对上述研究成果存在的局限性,并考虑到刀梁等位置不易布置温度传感器而导致温度未知,进而无法准确对刀梁泥饼进行判别这一难题,本文在已有的泥饼形成理论的基础上,采用ANSYS研究安装在滚刀刀筒内的温度传感器在不同工况下的温度变化规律,提出结合线性插值法和克里金插值法构建刀盘温度场。从空间和时间2个维度分析刀盘局部和整体的温度分布及变化特性,确立刀盘在正常掘进、外侧结泥饼及内侧结泥饼3种工况下的判断条件,提出分离相邻温度测量点正/负差值,以刀盘整体正/负差值之和呈现同方向变化为泥饼发育初始环评判指标; 结合所建温度场,引入从泥饼发育初始环到当前环一定数量点位的温度变化率总和作为泥饼发育程度评判指标。2个指标相结合实现结泥饼程度的判别,形成一种基于克里金插值法的常压刀盘刀梁区域泥饼发育程度算法,并对某大直径常压刀盘泥水盾构项目进行研究,与工程实际结泥饼情况进行对比,对算法的可行性和准确性进行验证。
1 刀盘结泥饼监测方法研究
本文拟采用滚刀温度的监测数据进行泥饼判别,为此需要通过Solidworks仿真不同工况下的滚刀温度变化特性。
1.1 不同工况下滚刀测温仿真
滚刀刀刃与掘进面摩擦是导致滚刀温度上升的主要原因,将温度传感器安装在滚刀刀座上可以实现对滚刀温度的间接测量。为了探究安装在滚刀刀座上的温度传感器在刀盘正常工作及结泥饼2种工况下温度检测的灵敏度,使用Solidworks对常压滚刀及刀筒进行三维建模,并导入ANSYS进行温度场分析。为了保证单一变量,设置2种工况下滚刀刀刃温度为100 ℃[26],环境温度为35 ℃,空气对流换热系数取为10 W/ (m2·K)。在结泥饼工况下刀筒上表面会被泥饼糊住,主要热源不再是滚刀刀刃与掘进面摩擦产生的热量,而是糊在滚刀及刀筒上表面的泥饼与掘进面摩擦产生的热量。因此,设置刀筒顶部温度为60 ℃来模拟刀筒顶部被泥饼糊住的情况,得到2种工况下的温度仿真结果,如图1所示。
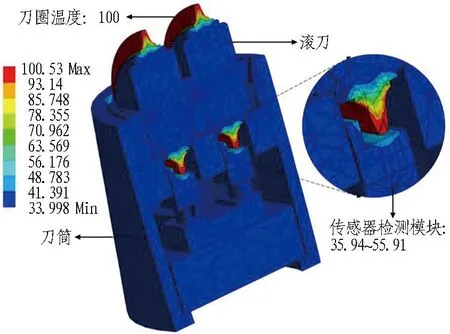
(a)刀盘正常工作工况
由图1可知,刀圈温度由内到外呈梯度变化,刀圈上离刀刃越近的点,其温度越高。正常工作工况下,旋转破岩的刀圈作为主要热源引起传感器位置的温度变化,图1(a)中传感器检测模块温度的平均值为45.93 ℃;而结泥饼工况下,附着在刀盘上的泥饼与掘进面摩擦生热并与刀圈共同影响传感器的温度变化,图1(b)中传感器检测模块温度的平均值为56.94 ℃。2种工况下传感器检测到的温度差接近11 ℃。因此,采用滚刀测温的方法能反映出不同工况下的刀盘温度情况,说明通过滚刀温度的监测数据进行泥饼判别具备可行性。
1.2 全刀盘温度仿真计算方法
常用的空间温度插值方法有克里金插值法及反距离权重插值法,这2种方法要求已知温度样本分布均匀并足够密集,然而由于刀梁位置不便安装温度传感器,导致在对刀梁区域的泥饼情况进行判别时缺少必要的数据支撑。因此,先基于多传感器布置方案尽可能多地获取刀盘温度数据,再依据已有数据构建刀梁区域的虚拟温度点,实现温度样本的扩展,然后利用克里金插值法或反距离权重插值法计算获得全刀盘温度场。
1.2.1 虚拟温度点构建方法
从空间相邻的2个刀箱上各取1个测温点位作为参考点,借助2个参考点构建虚拟温度点,如图2所示。
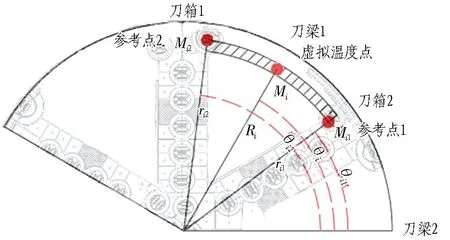
i为构建虚拟温度点的编号,i=1,2,…,n; Mi1和Mi2分别为虚拟温度点Mi的参考点1和参考点2; ri1、ri2分别为2个参考点的半径; θi1、θi2分别为2个参考点的角度。
虚拟温度点的计算公式如式(1)所示。
(1)
式中:Ti、Ri、θi分别为虚拟温度点i的温度、半径、角度;ti1、ti2分别为2个参考点的温度。
参考点的选取需满足以下2个条件: 1)为了避免误差叠加,虚拟温度点不能作为另一虚拟温度点的参考点; 2)2个参考点之间没有其他温度点,如图2中画斜线区域。斜线区域可表示为:
(2)
式中:r为半径;θ为角度。
1.2.2 刀盘温度场构建方法
1.2.2.1 Kriging插值法
Kriging插值法是一种基于统计理论的插值技术,通常Kriging模型变量X=[x1,x2,…,xg]与计算位置的真实值y之间的关系为:
y=λf(x)+μ(x)。
(3)
式中:f(x)为回归函数(一般采用多项式形式);λ为回归系数;μ(x)是均值为0、方差为σ2的随机函数。
μ(x)的协方差矩阵为:
cov[μ(x(e)),μ(x(f))]=σ2W[R(x(e),x(f))],(e,f=1,2,…,g)。
(4)
式中:e,f为采样点编号;W为沿对角线对称的相关矩阵;R(x(e),x(f))为采样点x(e)与x(f)的相关函数,常用平稳高斯函数表示。
1.2.2.2 反距离权重插值法
反距离权重插值法(inverse distance weighted,IDW)被广泛应用于各行业领域的空间分析与制图,其IDW算法公式为:
(5)
式中:Z为插值点估计值;Ze为第e个样本点观测值;de为插值点与第e个样本点之间的欧氏距离;n为用于估算插值点值的样本数;p为幂指数,当p=2时,IDW被称为距离平方反比法。
将刀盘视为极坐标,计算第e个样本点和插值点的欧氏距离de,若已知插值点的安装半径及安装角度分别为r、θ,则de的计算公式如式(6)所示。
(6)
1.3 刀盘泥饼发育程度算法
刀盘泥饼判别有2个核心问题: 1)如何确定泥饼开始发育的时间,即关注结泥饼状态,可以进行一定程度防结泥饼干预; 2)泥饼发育后的程度如何,即确定清理泥饼的工作量。
1.3.1 泥饼发育初始环评判指标
刀盘温度与泥饼之间相互影响,摩擦热导致刀盘升温,热量加剧泥饼固结,泥饼的产生导致刀盘温度场发生改变。因此,通过温度的变化映射泥饼的形成过程是可行的。
建立泥饼发育初始环的判别依据。刀盘未结泥饼时,外侧刀具由于切削距离长,其所在区域的温度高于内侧;当刀盘内侧出现结泥饼异常现象时,由于泥饼具有保温特性使刀盘内侧的温度损失减小,进而导致内侧温度高于外侧。其公式表示为[16]:
(7)
式中ΔT为外侧温度与内侧温度的差值。
式(7)仅表示了刀盘内侧结泥饼的判断依据,当刀盘外侧结泥饼时,不满足ΔT<0的条件。因此,在式(7)的基础上,分析理想条件下若干刀盘外侧测温点与内侧相邻测温点温度差的统计值∑ΔT在正常掘进、外侧结泥饼及内侧结泥饼3种工况下的分布及变化趋势。可知: 未结泥饼时,∑ΔT应围绕某一正值上下波动;刀盘内侧结泥饼时,∑ΔT由大变小; 刀盘外侧结泥饼时,∑ΔT越变越大,具体如式(8)所示,亦可用图3表示。
(8)
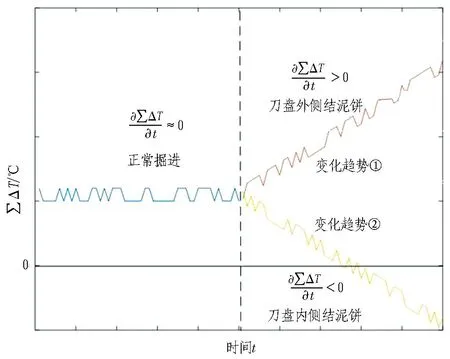
图3 理想条件下不同工况时∑ΔT的分布及变化曲线

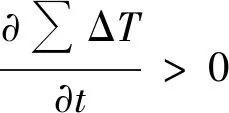
(9)
式中:j为滚刀分区编号,一般分为若干个刀箱及中心区域,j=1,2,…,m;l为刀箱j上的测温点编号,刀盘外侧测温点编号大于内侧测温点编号,l=2,3,…,w;p为环号,p=1,2,…,h。
(10)
(11)
(12)
假设在y环满足式(12)的条件,说明在y-1环出现温度异常,即刀盘外侧泥饼发育初始环为y-1环。
1.3.2 刀盘泥饼发育程度评判指标
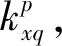
(13)
式中:q为在刀梁x上的分析点编号,q=1,2,3,…,s;x为刀梁编号,x=1,2,3,…,z。
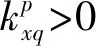
(14)
2 案例分析
2.1 工程地质条件
某泥水盾构项目右线隧道全长3 957.8 m,主要穿越粉砂、细砂、石英砂岩、粉砂岩、泥质粉砂岩、凝灰角砾岩和粉质黏土等多种地层,项目右线隧道纵剖面地质分布如图4所示。主要土层物理力学性质指标汇总如表1所示。

表1 主要土层物理力学性质指标汇总
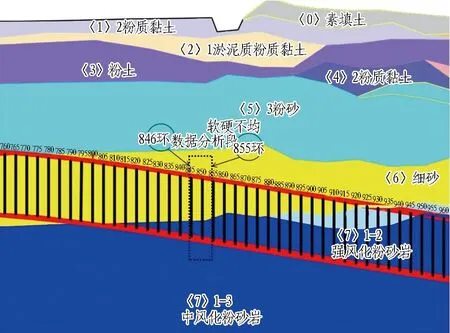
图4 某泥水盾构项目右线隧道纵剖面地质分布图
2.2 多传感器测温布置方案
项目采用直径为15.07 m的常压刀盘大直径泥水盾构施工,刀盘由1个中心块和6个刀盘主壁组成,除了刀箱3上装有1个单滚刀刀筒外,其余均为双滚刀刀筒。综合考虑刀盘结构及使用空间插值法时对温度样本分布及数量的要求: 边缘及中心滚刀数量少,且分布不规律,必须保证边缘和中心位置的每个滚刀刀筒内至少安装1个传感器;正面滚刀数量多且分布规律,可选择一部分安装传感器;同时,需满足温度数据分布均匀且足够密集的条件。依据上述要求,最终确定传感器分布方案如图5所示。
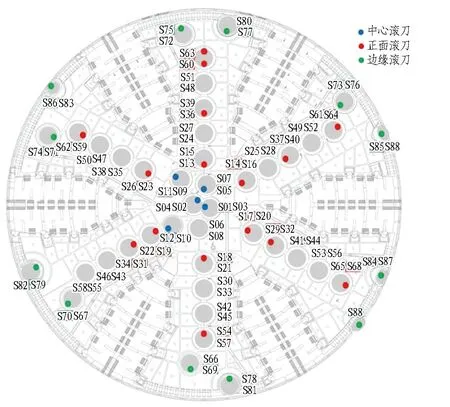
图5 多传感器测温布置方案
图5中,分别有5、15、12个传感器分布在中心滚刀、正面滚刀和边缘滚刀上。其中,全部中心滚刀、边缘滚刀刀筒内均布置了温度传感器,其余的温度传感器较为均匀地布置在正面滚刀刀筒内,一共32个温度测量点。
2.3 全刀盘温度仿真计算
实际的工程项目为泥水盾构项目,刀盘泥水冲刷分为泥浆管路冲刷和刀筒内管路冲刷。刀筒内管路冲刷一般是掘进结束之后进行,因此,对刀盘掘进过程中温度场的影响可以忽略。泥浆管路冲刷在掘进过程中一直开启,意味着对刀盘温度场的影响程度随时间变化较小,其带来的温度变化不会掩盖刀盘表面形成泥饼后温度升温快、降温慢的变化趋势,因此,可忽略刀盘泥水冲刷对刀盘温度的影响。
2.3.1 构建虚拟温度点
选取刀盘在第851环某时刻的传感器数据,如表2所示。
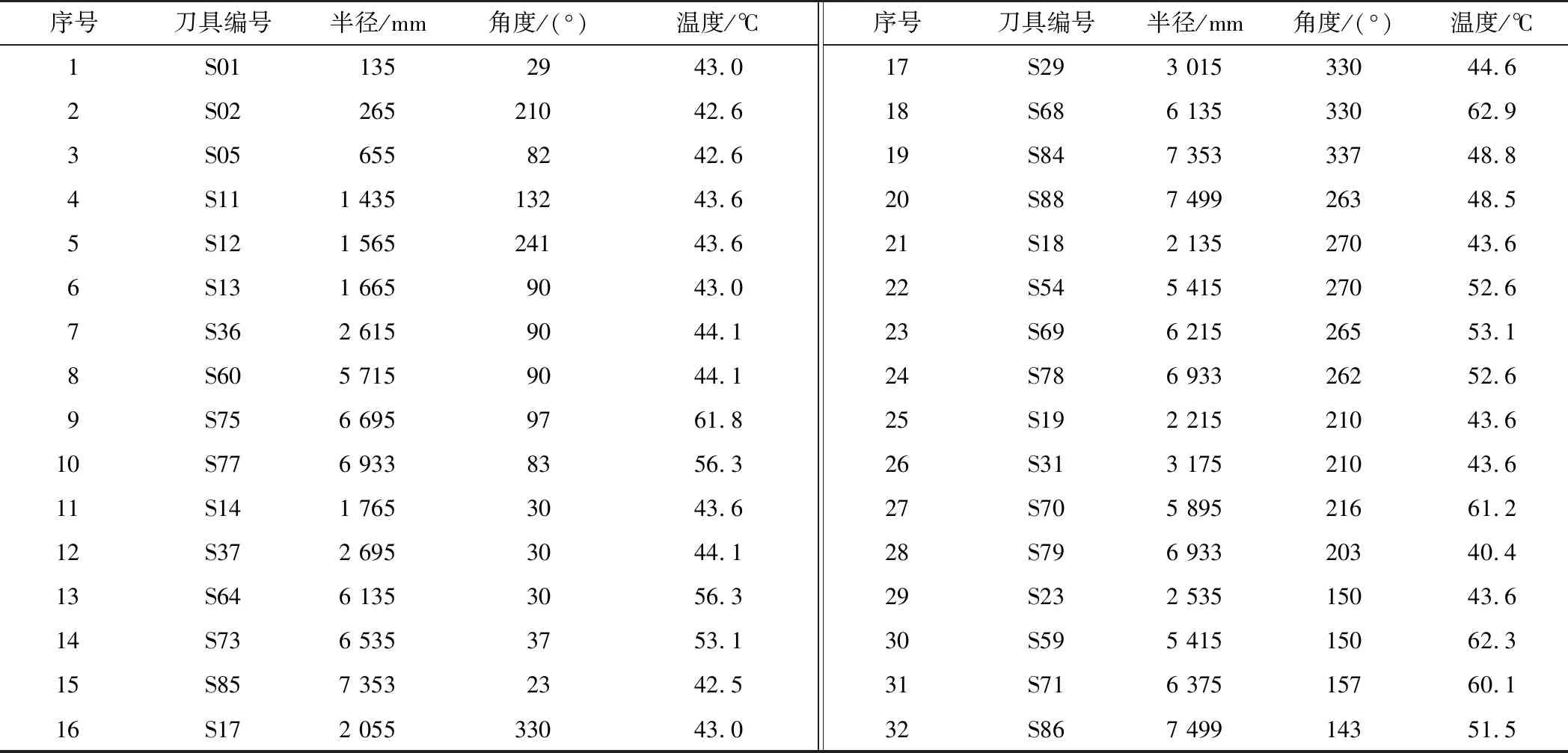
表2 传感器测温点的坐标及温度数据
根据已知的传感器测温点,加入如表3所示的虚拟温度点,故虚拟温度点数量n为8,扩展样本后的刀盘温度点有40个。
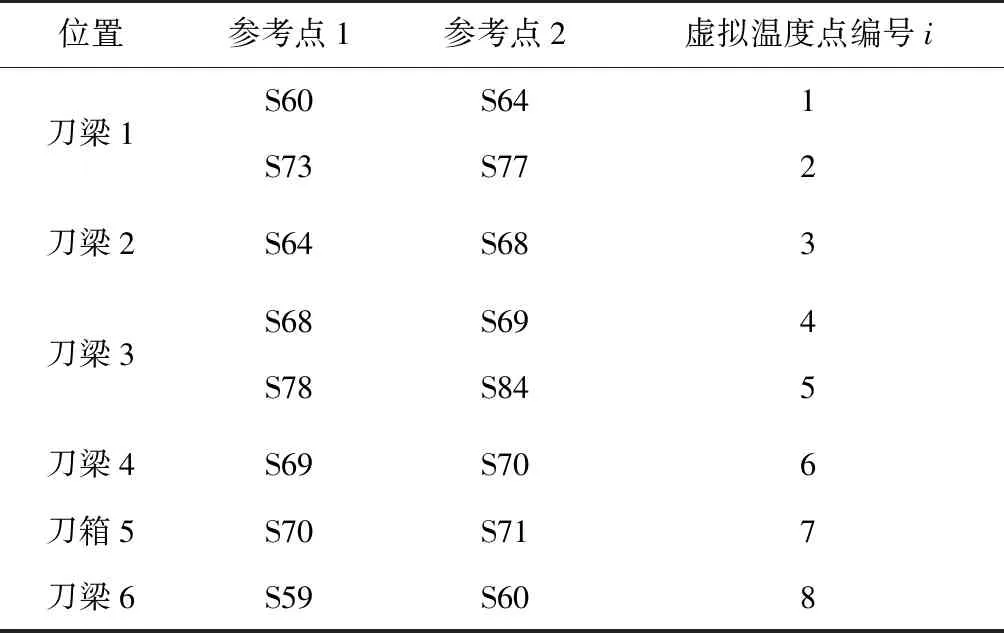
表3 虚拟温度点汇总
2.3.2 构建刀盘温度场
利用Matlab中Kriging插值工具箱的dacefit和predictor函数,可实现Kriging插值运算,回归模型采用regpoly1,相关函数为高斯函数,theta=[10,10]。根据式(5)和式(6),自编代码实现反距离权重插值法的全刀盘温度计算。仅以测温点温度数据作为样本,2种空间温度插值方法计算结果如图6所示。
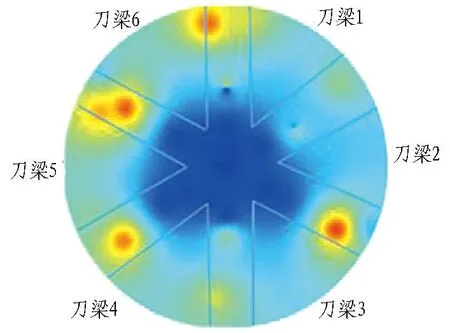
(a) 反距离权重插值法
由图6可知,未加入虚拟温度点作为插值样本前,计算结果显示刀盘局部高温集中,同时延展性和衔接性较差,分析原因是由于缺乏刀梁位置的样本数据。
结合表2和表3的数据,将测温点及虚拟温度点共40个温度数据作为计算样本,构建刀盘温度场如图7所示。
采用孟加拉红培养基[18],分别接种10-5、10-6、10-7、10-8 四个稀释梯度的悬浮液,将接种好的培养皿于30 ℃培养24 h后进行酵母菌计数。计数时选取培养基上湿润、光滑、不透明、大而厚的菌落进行酵母菌计数。
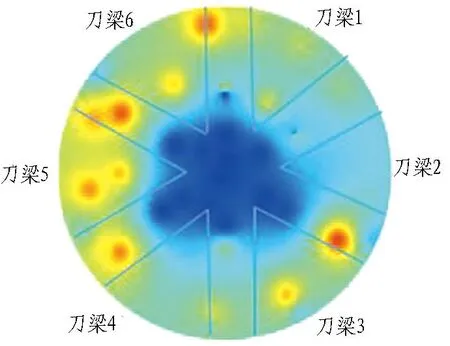
(a) 反距离权重插值法
由图7可知,扩展样本后反距离权重插值法的计算结果改善仍然不明显,而克里金插值法计算的结果延展性较好,分布也更符合结泥饼的温度传递规律。因此,采用线性插值扩展刀梁位置温度数据的方法能很好地解决用于构建温度场的样本数据分布不均、数量不足的问题。
2.4 刀盘结泥饼程度计算
对案例项目中盾构在846—855环掘进期间进行结泥饼程度判别,根据图4可知,虽然盾构在846—855环掘进时主要穿越细砂和中风化粉砂岩2种地层,但在实际工程中,通过抽刀的形式观察滚刀结泥饼情况,发现该地层依旧处于淤泥质粉质黏土层。
2.4.1 泥饼发育初始环评判指标的计算
由图5可知,滚刀分区数量m为7,包括6个刀箱区域及1个中心区域。依据上述已知信息对该案例进行泥饼判别分析。根据获得的传感器温度数据,通过式(9)计算刀箱1上各测温点在第851环时的温度及与相邻测温点的温度差,如表4所示。

表4 刀箱1上各测温点在第851环时的温度及与相邻测温点的温度差汇总

表5 泥饼发育初始环计算汇总
根据式(11)和表5,计算得到∑ΔT,并绘制曲线如图8所示。
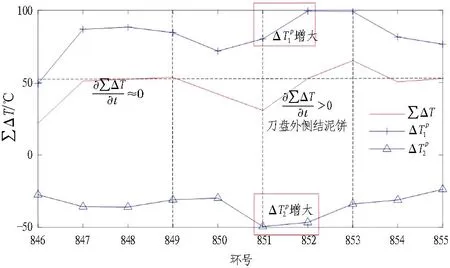
图8 ∑ΔT的分布及变化曲线
由图8可知,在第852环满足式(12)的条件,因此,确定刀盘外侧泥饼发育初始环为851环。
2.4.2 刀盘泥饼发育程度评判指标的计算
为了确定刀盘刀梁区域的泥饼发育程度,在基于克里金插值法得到全刀盘温度数据的前提下,选取刀梁区域上的温度分析点来计算对应区域的泥饼发育程度评判指标,在各刀梁区域分别选取6个温度分析点。因此,温度分析点数量s为6个,刀梁数量z为6个,共36个温度分析点,如图9所示。

温度分析点11是指刀梁1上编号为1的温度分析点。
根据计算所得的刀盘温度场数据,通过式(14)计算图9中851—855环所有分析点的Kx值,结果如表6所示。
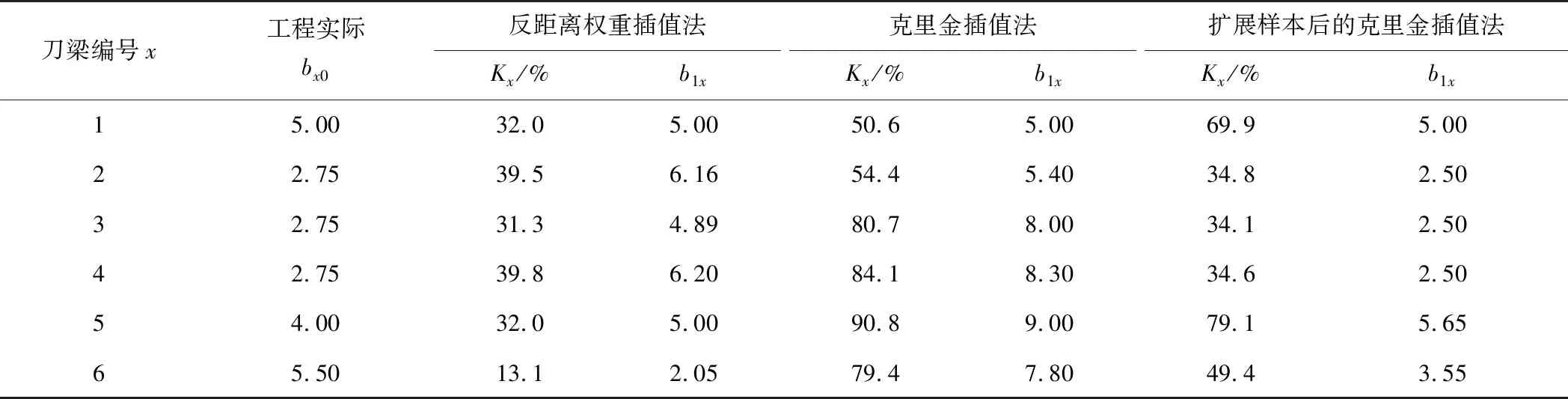
表6 工程实际比例bx0及各种插值方法下的b1x汇总
2.5 误差率计算
将判别结果与实际情况进行对比。由于温度变化率与泥饼程度是2个不同的度量单位,因此,考虑进行数量级归一化处理。采用各刀梁实际泥饼面积比得到实际比例值bx0,这个比例可反映各刀梁结泥饼情况,然后再将刀盘泥饼发育程度评判指标Kx作为计算比例与实际比例统一度量,得到以刀梁v的实际比例值作为基准统一度量后的刀梁x计算比例值bvx,计算以刀梁v作为基准时的判别误差率δv。计算公式如式(15)所示。
(15)
由于盾构刀盘直径达15 m,只能通过观测局部区域的结泥饼情况,然后汇总得到全刀盘泥饼分布情况。刀盘某刀梁局部泥饼现场图如图10所示。图10(a)中刀梁区域整格均被泥饼覆盖,即图中矩形框覆盖区域;图10(b)中刀梁区域接近半格被泥饼覆盖,即图中2个矩形框覆盖区域。设定以矩形面积衡量每个刀梁的泥饼面积相对大小,设定图10(a)中大矩形所代表的物理量大小为1,图10(b)中小矩形的面积为大矩形的1/4。

(a) 整格结泥饼
分别观察各刀梁上的结泥饼情况,整合后绘制刀盘整体泥饼分布图如图11所示。图11中绿色部分为刀盘上主要结泥饼的位置,图10(a)中的黑框对应图11中的大矩形框,图10(b)中的黑框对应图11中的小矩形框。由图11可知: 结泥饼最严重的区域为刀梁1和刀梁6区域;刀梁2、3、4区域结泥饼情况相近,与其他区域相比结泥饼情况最轻微; 刀梁5区域结泥饼情况介于两者之间。将计算比例以刀梁1的实际比例值作为基准,统一度量得到b1x,并得到刀梁1—6的结泥饼实际比例值bx0,如表6中所示。
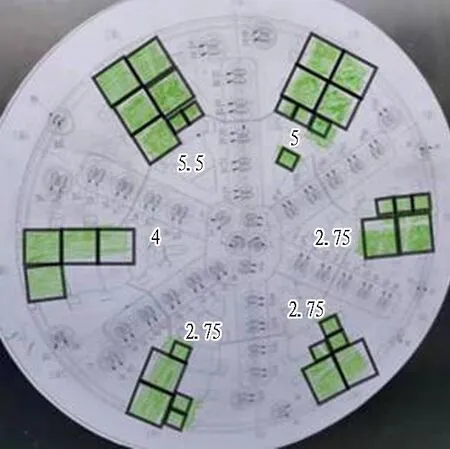
图11 刀盘整体泥饼分布图
表6中b1x是以刀梁1的实际比例值作为基准进行统一度量后的值,基准不同所计算的误差率也不相同,故分别以刀梁1—6的实际比例值作为基准,根据式(14)计算对应的误差率,如表7所示。

表7 误差率δv汇总
由表7可知,由于未扩展插值样本,计算结果的误差率超过100%,如表7中的“131.18”。对比3种方法,刀梁区域实际泥饼情况与基于样本扩展后的克里金插值法的计算结果最为接近,准确率达70.87%,说明扩展样本的必要性及所建刀盘泥饼发育程度评判指标的实用性。
3 结论与建议
以某泥水盾构工程为背景,提出一种基于克里金插值法的常压刀盘刀梁区域泥饼发育程度算法,实现刀盘结泥饼判别从定性分析到定量分析的转变,为清洁泥饼提供时间及点位参考。通过本文的研究,可得到以下结论。
1)通过仿真对安装在刀筒内的温度传感器在正常掘进、结泥饼2种工况下的温度变化规律进行验证,结果表明滚刀温度数据能反映刀盘结泥饼工况下的温度异常。利用多点位的传感器温度数据,提出线性插值扩展刀盘刀梁区域温度数据的方法,保证空间温度插值法形成刀盘温度场的应用效果。
2)从空间和时间2个维度分析刀盘温度分布及变化特性,得到刀盘在正常掘进、外侧结泥饼及内侧结泥饼3种工况下的判断条件,提出分离相邻测温点正/负差值,以刀盘整体正/负差值之和呈现同增趋势作为刀盘外侧区域泥饼发育初始环的评判指标。
3)结合所建温度场引入一定数量的温度分析点,从泥饼发育初始环到当前环的温度变化率总和作为泥饼发育程度评判指标。根据某泥水盾构项目结泥饼的实际案例,对结泥饼程度判别的算法流程进行验证,并将计算结果与实际结果进行对比,平均准确率高达70.87%。
盾构掘进过程中,可以结合本文提出的泥饼发育程度算法,研究不同泥饼发育程度下的防治措施,实现更灵活且有针对性的泥饼监控及防治方案设计。
