基于ABC-BP神经网络的地铁盾构隧道地层识别及复合比预测
2024-05-07郭小霖简永洲丰土根陈子昂
郭 勇, 郭小霖, 简永洲, 张 箭, *, 丰土根, 陈子昂
(1. 上海华铁工程咨询有限公司, 上海 200040; 2. 河海大学 岩土力学与堤坝工程教育部重点实验室, 江苏 南京 210098; 3. 中交二公局第四工程有限公司, 河南 洛阳 471013)
0 引言
在轨道交通的建设中,盾构法因其施工速度快、安全性高且不易受气候变化影响的优点被广泛应用于地铁隧道施工中。地铁建设的迅猛发展对盾构施工安全性提出了更高的要求,而地质环境复杂是盾构事故的重要风险源之一[1]。因此,在掘进过程中,实时识别开挖面的地层并准确描述复合地层的复合状况,对盾构隧道的施工有着极为重要的意义。
在盾构掘进过程中,其掘进参数与所处地层的物理力学参数密切相关,存在一定的映射关系。国内外专家、学者针对掘进参数与被开挖岩体或土体的物理力学参数之间的关系进行了一系列的探索。Shaterpour等[2]使用数理统计方法,研究了TBM运行时的总推力和刀盘转矩在不同地层下的变化情况; 赵博剑等[3]对复合地层中的掘进参数进行了数理统计与分析; 杨果林等[4]、张沛然等[5]从可掘性指标与相关性入手,分析施工参数在不同地层中的变化特征,并采用经验模型对地层可掘性进行预测。已有的研究对机-岩关系进行了总结并基于掘进参数对地层进行了预测,但分析集中于单一地层。在工程实际中,复合地层段地质环境复杂,开挖断面地质多变性和突变性显著,掘进参数难以匹配,更需对开挖面进行准确的预测。但是,组成复合地层的数种地层往往地质特征相差悬殊,这给复合地层下机岩关系的探究造成困难。
为了表征开挖面的地层情况,诸多学者定义了多种指标来表述地层情况,并建立了相应的地层识别模型。Hassanpour等[6-7]通过TBM掘进过程的参数定义场切深指数FPI来表征围岩等级,并分析了FPI与岩体力学参数的相关性; Wang等[8]基于土压平衡盾构的运行参数建立了地质特征综合指标计算模型,并用其区分多个地质特征组; 邢彤等[9]利用场切深指数和转矩切深指数(TPI)建立表示掘进土层状况的特征空间,并通过特征空间识别地层类型,同时采取函数表达式对被开挖土体进行实时分类; 许明等[10]通过地层比功判定持力层,实现地层识别。可以看到,地层情况表征多通过理论公式和参数定义表示,而直接反演复合地层中软硬地层组合情况的研究较少,难以直观反映复合地层的地质状况。因此,选用一种能够直接表征复合地层组合情况的参数并对这种参数加以预测十分必要。
近年来,随着大数据技术不断革新,5G技术日渐普及,人工智能呈飞跃式发展,智能化建设已成为盾构隧道工程发展的必然趋势。随着机器学习研究的不断深入,聚类[11]、决策树[12]、贝叶斯分类[13]、支持向量机[14]、集成学习[15]等机器学习算法广泛应用于地层识别预测中,各类优化算法也得到了突飞猛进的发展。目前,BP神经网络因其强大的非线性映射能力与泛化能力在地层识别中广泛应用,例如: TBM围岩分级[16]、地层情况预测[17-19]以及岩性识别[20]。但是,针对复合地层情况的预测分析还较少,同时BP神经网络存在易陷入局部最小值的劣势。人工蜂群算法作为一种全局寻优算法,如果应用到BP神经网络之中,可以改善其易陷入局部最优的缺点,进而提升预测准确率。
综上可知,复合地层的机-岩关系及表征方法研究比较缺乏。本文先探究掘进参数在不同地层下的变化,采用复合比描述开挖面地层复合情况,构建地层识别BP神经网络预测模型以及复合比预测模型,并采用人工蜂群算法对BP模型进行优化,同时结合施工区间掘进数据对开挖面地层与复合情况进行预测。该模型可用于开挖过程中对地层的实时监测与识别,实现在掘进过程中反馈开挖面地层情况并描述地层复合情况,以此调节掘进参数,最终指导施工。
1 工程概况
南京地铁6号线是南京地铁线路网中的一条在建线路,自北向南途经栖霞、玄武、秦淮、雨花台以及江宁5个行政区,建成后将有效缓解中心地区的的交通拥堵,加强主城区与其他外围团块的联系,提升地铁的运营能力。南京地铁6号线北段规划如图1所示。
图1 南京地铁6号线北段规划图
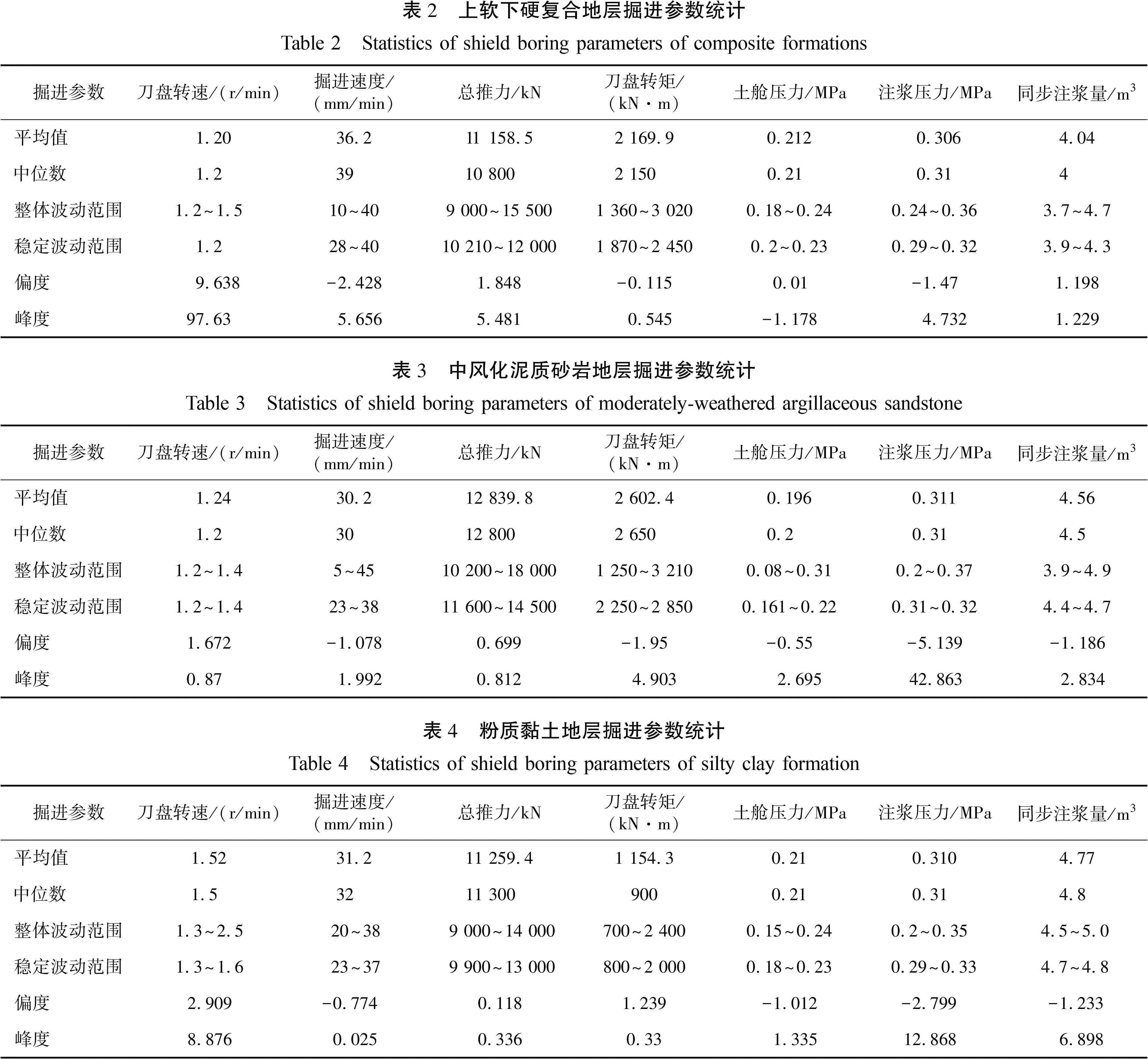
南京地铁6号线某施工区间全长4 008 m,采用地下敷设方式。隧道施工下穿地层主要有: 强风化泥质砂岩、中风化泥质砂岩、强风化安山岩、中风化安山岩、粉质黏土等。其中,盾构隧道施工段主要分为3种地层: 中风化泥质砂岩、上软下硬地层、粉质黏土地层。该工区中,复合地层区段主要由中风化泥质砂岩与强风化泥质砂岩复合、强风化泥质砂岩与粉质黏土复合组成。地层参数如表1所示。
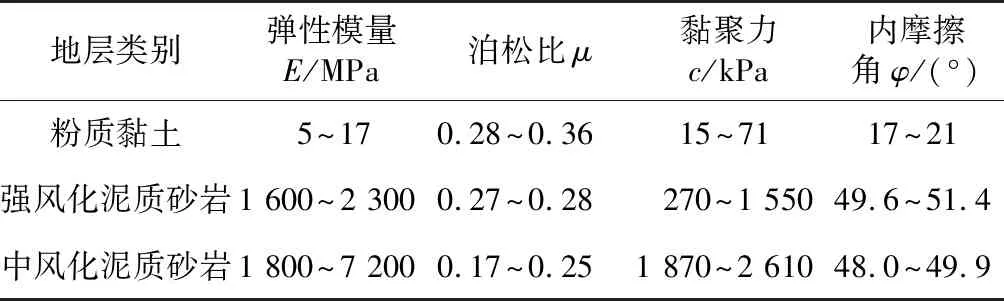
表1 地层参数统计
此盾构主驱动采用液压驱动方式,刀盘开口率为38%,开挖直径为6 440 mm,转速为0~3.44 r/min,标准转矩为6 841 kN·m,脱困转矩为8 684 kN·m,最大推力为42 575 kN。盾构管片外径为6 200 mm,内径为5 500 mm,厚度为350 mm,环宽为1 200 mm。
2 模型原理
2.1 BP神经网络原理
BP(back propagation)神经网络是一种多层前馈式神经网络,其通过误差逆向传播算法训练。该类神经网络的拓扑结构属于层次型结构,主要由输入层、隐含层、输出层3部分组成。隐含层的神经元称为隐单元,通过对隐含层单元状态的改变,影响输入层与输出层的关系。BP神经网络的信号传播由正向传播过程以及反向传播过程共同组成。输入层输入信号通过连接权传递至隐含层,再传递至输出层,实现输入信号的输出。此时,对输出参数真实值与模型输出值进行误差比较,若误差超出期望范围,则通过反向传播算法更新修正连接权,再正向传播输出。BP神经网络通过正向和反向传播过程的反复来完成网络训练学习,进而实现预测与分析。
作为目前应用最为广泛的神经网络模型之一,BP神经网络具有神经网络算法的普遍优点,即强大的非线性映射能力、优秀的自主学习与适应能力以及处理并行信息的能力。但是,由于其误差反向传播算法采用梯度下降法,存在易陷入局部最小值的缺陷,影响训练效果,降低预测精度,故采用全局寻优算法对BP神经网络进行优化,以提高其预测分析能力。
2.2 人工蜂群算法原理
ABC算法即人工蜂群算法(artificial bee colony),源于蜜蜂采蜜时分工明确、相互协作,精准找到周边优质蜜源的生物行为,是一种全局寻优求解的搜索算法。ABC算法有着强大的求解寻优能力,在人工神经网络领域应用广泛。
ABC算法主要由引领蜂、跟随蜂、侦查蜂3个阶段组成。引领蜂阶段用于维持优良解,跟随蜂阶段用于提高收敛速度,侦查蜂阶段用于增强摆脱局部最优的能力。算法的主要参数包括: 蜜源数、迭代终止次数、局部最优解评判参数和求解维度等。
2.3 人工蜂群算法优化后的BP神经网络
传统BP神经网络采用梯度下降法作为误差反向传播算法,容易陷入局部最小值,导致误差函数并非全局最小,预测精度难以保证。ABC算法作为一种全局寻优算法,能够求出区域内最优解,进而有效避免陷入局部最优与梯度爆炸,提高预测精度和模型的泛化能力。采用ABC算法对BP神经网络的权值和阈值进行寻优,能够提高其预测分析能力,增强模型对问题的适应能力。通过赋予全局最优权值与阈值,达到全局最优解,提高神经网络预测精度,避免陷入局部最优,从而实现对BP神经网络的优化。ABC算法优化的神经网络建立流程如图2所示。
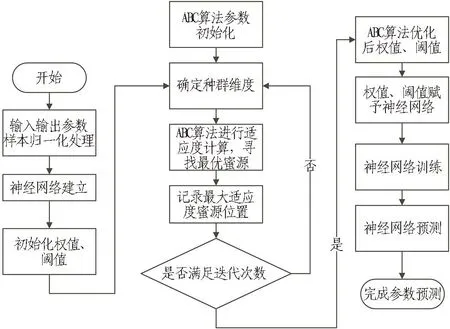
图2 ABC算法优化的神经网络建立流程
2.4 地层识别与复合比预测模型原理
地层识别与复合比预测模型由地层识别模型部分以及复合地层复合比预测部分组成。首先,通过地层识别模型输入盾构掘进过程中的掘进参数,对开挖面地层进行分类识别,确定地层种类;然后,由复合比预测模型对分类所得复合地层的复合比进行预测,进一步对复合地层组成情况进行表征,从而达到描述开挖面地层的目的。地层识别与复合比预测模型结构如图3所示。
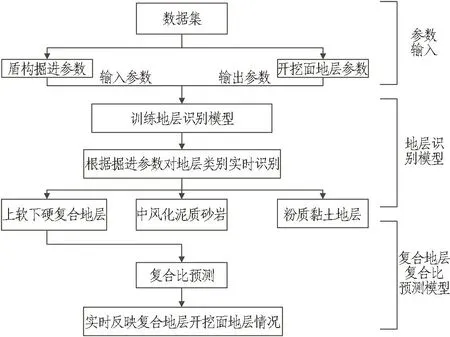
图3 地层识别与复合比预测模型结构
3 模型参数与评价指标的分析与确定
本文所构建的模型参数主要包括输入层参数(掘进参数)、输出层参数(复合比),模型评价指标包括平均绝对误差(MAE)、均方根差(RMSE)以及样本回归值(R2)3种。
3.1 掘进参数
在掘进过程中,掘进参数受地层参数影响。对盾构4个系统(推进系统、刀盘系统、排土系统、注浆系统)中与地层相关性强、统计特征变化较为明显的7个参数进行分析,确定其在上软下硬复合地层、中风化泥质砂岩以及粉质黏土3种地层中的统计特征,以此探寻掘进参数与地层间的关系。选取平均值、中位数、下四分位数Q1与上四分位数Q3作为各地层下掘进参数的统计指标。
3.1.1 推进系统参数分析
推进系统参数包括总推力和掘进速度。地层情况对盾构总推力和掘进速度有着重要的影响。地层越坚硬,其掘进速度越慢。在实际工程中,需尽量保持掘进速度恒定且快速。如果地层硬度较高,则需要增大盾构总推力以保证掘进速度;如果地层硬度较低,则盾构总推力可在保证掘进速度的前提下相应减少。
在不同地层中,总推力的变化与分布情况存在明显差异,如图4所示。在均值与中位数方面,均呈现出中风化泥质砂岩>粉质黏土>上软下硬复合地层的情况。 在数值分布方面,在粉质黏土地层整体分布相对均匀;在上软下硬复合地层,中位数偏向下四分位数Q1,呈现左偏态势;在中风化泥质砂岩地层下呈现右偏态势。上软下硬复合地层强度差距大,对推力的需求不稳定,分布波动较其他地层大;中风化泥质砂岩地层硬度较大,所需总推力随之上升;粉质黏土地层土质松散,强度较低,掘进时所需总推力较其他地层小,应避免对土层的过度扰动。
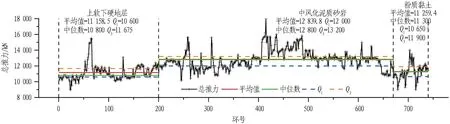
图4 总推力统计分析
相较于总推力在3种地层下的明显差异,掘进速度在不同地层下的集中趋势变化相对较小,如图5所示。其均值与中位数为30~40 mm/min;分布情况方面均呈现左偏态势,偏度大小以复合地层段为甚,中风化泥质砂岩段次之。在地层硬度较低的粉质黏土段,盾构掘进速度大且在3种地层中最为稳定;在中风化泥质砂岩段,采用较低速度进行掘进;在上软下硬复合地层段,掘进速度受地层的较大硬度变化影响,波动剧烈,掘进速度不稳定。
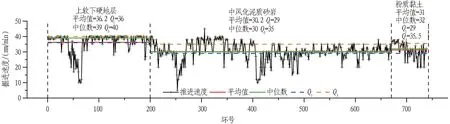
图5 掘进速度统计分析
3.1.2 刀盘系统参数分析
刀盘系统参数包括刀盘转矩和刀盘转速。不同的地层会影响刀盘转速和转矩,从而影响盾构的性能。在较硬地层中,刀盘转矩要相应提高才能更好地破碎岩体。刀盘转矩往往能反映掘进过程的顺利程度,如遇转矩过大,则可能是出现了刀具磨损或者结泥饼现象。刀盘转速一般是在施工过程中通过人工设置,与掘进速度相结合的贯入度是反映地层掘进难易程度的指标之一[21]。
在3种地层下刀盘转矩的集中趋势差异较大,在粉质黏土段区间尤为明显,如图6所示。3种地层下的均值与中位数均呈现出中风化泥质砂岩>上软下硬复合地层 >粉质黏土地层的情况。分布趋势上,中风化泥质砂岩段刀盘转矩分布最为集中,上软下硬复合地层段次之,粉质黏土段刀盘转矩波动最大。究其原因,在硬岩区段地层强度较高,刀盘转矩需求大且稳定;粉质黏土段土质松散易于掘进,转矩降低且波动明显;复合地层区段既存在软弱土层的不稳定性,又存在硬岩地层的高强度,所需刀盘转矩介于两者间且波动明显。
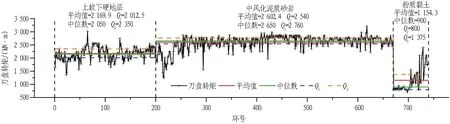
图6 刀盘转矩统计分析
刀盘转速一般在盾构掘进过程中通过人工设置,故刀盘转速的波动情况小。如图7所示,整个统计区间内,刀盘转速变化不大。在粉质黏土地层刀盘转速略高于其他2种地层,且其波动范围也较其他2种地层大。其原因在于粉质黏土地层土质较软,在刀盘转矩较小的情况下,增大刀盘转速有利于掘进效率的提高。
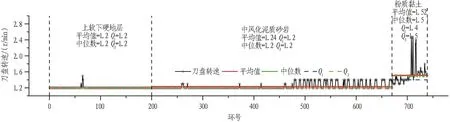
图7 刀盘转速统计分析
3.1.3 排土系统参数分析
排土系统参数选取土舱压力。在土压平衡盾构掘进过程中,尤其是在软弱土层中掘进时,土舱压力直接关系到开挖面的稳定性和地表的沉降。在掘进过程中,应保持掌子面的稳定性,避免因开挖面失稳产生坍塌或过大的地表沉降。
在不同地层下,土舱压力的集中趋势呈现出一定的差异,如图8所示。就均值而言,土舱压力呈现出上软下硬地层>粉质黏土地层>中风化泥质砂岩的情况。除中风化泥质砂岩段初期有较大幅度波动外,其余区间分布状态均较为稳定。针对不同地层下的土舱压力变化进行原因分析: 1)中风化泥质砂岩地层硬度较高,稳定性较好,掘进时可采用相对较小的土舱压力,故该地层条件下土舱压力小于其他地层; 2)粉质黏土和上软下硬地层中的软弱土体相对于中风化泥质砂岩稳定性较差,可能引起地表沉降,因此需要较高的土舱压力以维持开挖面的稳定。
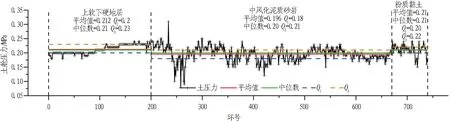
图8 土舱压力统计分析
3.1.4 注浆系统参数分析
注浆系统参数包括同步注浆量和注浆压力。同步注浆量与地表沉降密切相关,根据不同地层选取合适的同步注浆量可以有效减少地表沉降,降低施工的不利影响。注浆压力的合理与否关系到管片的上浮和地表的沉降,与同步注浆量一同对盾构隧道的正常施工与周边建筑物安全有着重要的影响。
同步注浆量总体变化浮动不大,在3种地层下略有差异,如图9所示。在集中趋势方面,各地层下均值和中位数接近,均呈现粉质黏土地层>中风化泥质砂岩>上软下硬地层态势。波动性方面,粉质黏土段波动较小;上软下硬地层段与中风化泥质砂岩段的波动则明显更大。其原因在于,复合地层中软硬土层强度差异变化大,注浆量波动相对较大;粉质黏土地层因其孔隙与渗透率较高,同步注浆量略大于其他2种地层;中风化泥质砂岩同步注浆量受埋深影响,因其深度逐渐增加,均值较上软下硬地层更高。
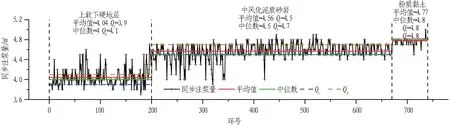
图9 同步注浆量统计分析
注浆压力在3个地层中的集中趋势变化不大,均值总体平稳,如图10所示。在波动范围方面,以上软下硬地层的注浆压力变化为最,因该地层软硬地层同时存在,注浆压力也随地层性质不同而改变。在掘进之初,注浆压力为高于外界水压0.3~0.7 MPa,并随掘进过程不断调整。在掘进过程中,注浆压力不断优化至1.1~1.2倍静止水土压力。
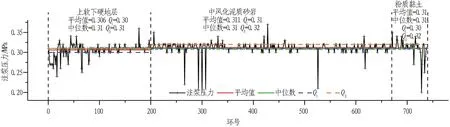
图10 注浆压力统计分析图
3.1.5 各地层下掘进参数范围
通过对各地层下掘进参数的统计与分析,确定了不同地层下各掘进参数的集中趋势与分布趋势。采取百分位数进一步对掘进参数的波动范围进行描述。选用百分位数P10作为各掘进参数下限,P90作为各掘进参数上限,确定3种地层下掘进参数的稳定波动范围。表2—4示出了各地层下不同掘进参数的各项统计指标。
3.2 复合比
复合地层广泛存在于我国东南地区,因此在盾构掘进的过程中,不可避免地会遇到复合地层。复合地层对掘进参数影响变化较大,为了能够反映复合地层对掘进参数的影响,定义复合比φ来表征复合软硬地层组合比例,其物理意义为较软土层占开挖面土层的百分比。复合比φ计算公式为:
(1)
式中:Ssoft为开挖面中较软土层面积;Stotal为开挖面总面积,Stotal=Ssoft+Shard,Shard为开挖面中较硬土层面积。
复合比φ表示隧道开挖面处断面范围内软硬土层所占比例。其中,φ=0表明隧道开挖面断面范围内全是较硬的岩层;φ=1表明隧道开挖面断面范围内全是较软岩层或土层。盾构断面复合地层如图11所示。复合比能够很好地表征复合地层的组合情况,即通过某点的值表示该环处掘进断面上不同地层的组合情况; 通过某区间的复合比曲线表示在掘进轴线方向上地层的不同组合情况。
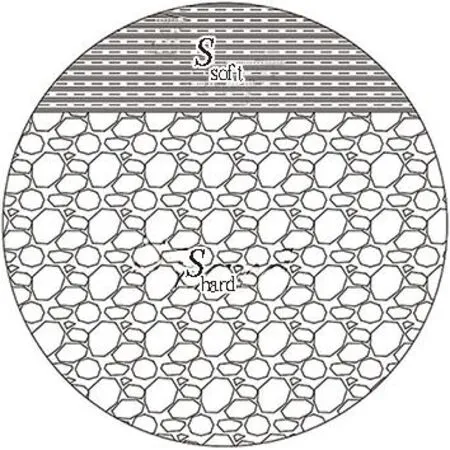
图11 盾构断面复合地层示意图
3.3 参数归一化
盾构掘进参数数量多且分属不同系统,其单位、数量级等均有较大差异。如果各参数量纲不同,直接输入参数将会使训练过程中出现梯度爆炸的问题。为了便于对比分析,需要对掘进参数进行归一化处理再进行预测分析。
采用式(2)进行最值归一化处理:
(2)
式中:Xi为原始数值;Xmax为样本某一掘进参数中的最大值;Xmin为样本某一掘进参数中的最小值;X*为归一化后的数值。
3.4 模型评价指标
采用平均绝对误差(MAE)、均方根差(RMSE)以及样本回归值(R2)作为预测模型的评价指标。
平均绝对误差(MAE)是预测值和真实值之间绝对误差的平均值。MAE是一种线性分数,所有个体差异在平均值上的权重都相等。MAE能够表示预测精度,MAE越低,表示预测值与真实值越接近,预测结果更精确,其计算公式如下所示:
(3)
式中:y为真实值;y′为ABC-BP模型的预测值;N为数据总量。
均方根误差(RMSE)是预测值与真实值之差的平方与样本总量N比值的平方根,计算2组数据之间的偏差程度。与MAE相比,RMSE对较高的误差值有更多惩罚。RMSE越低,表示预测值与真实值越接近,预测结果更精确,其计算公式为
(4)
样本回归值R2反映预测值和真实值的拟合程度,样本回归值R2的区间为[0,1]。R2越接近于1,表示预测值和真实值拟合程度越高;R2接近于0,表示预测值和真实值拟合程度低,具体如下:
(5)
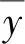
4 地层识别模型预测分析
采用地层识别模型建立掘进参数与开挖面地层之间的关系,对开挖面地层进行分类,实现根据参数在掘进过程中对开挖面地层进行判别; 将模型所确定的地层种类作为复合地层复合比预测的基础。
以掘进参数刀盘转矩、刀盘转速、总推力、注浆量、注浆压力、掘进速度、土舱压力作为地层识别模型的输入参数,对地层进行分类。为了对神经网络进行训练,将地层类别进行编码: 上软下硬复合地层-1,中风化泥质砂岩-2、粉质黏土-3。以分类结果上软下硬地层、中风化泥质砂岩、粉质黏土为输出层构建神经网络。因此,地层识别模型输入层神经元为7个、输出层神经元为3个,隐含层节点数选定为15个。最大迭代次数为700,学习率为0.01,迭代精度为0.001。地层识别模型拓扑结构见图12。
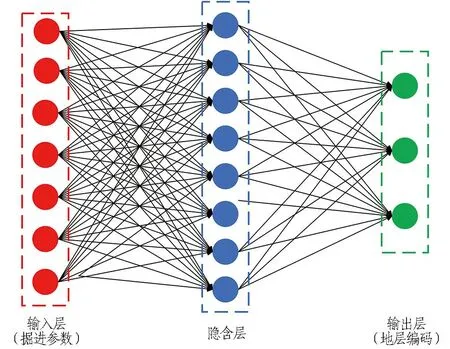
图12 地层识别模型拓扑结构
以施工区间3种复合地层,即上软下硬地层、中风化泥质砂岩、粉质黏土地层,与其掘进参数共758组数据作为数据集。随机选取数据集中70%为训练集进行训练,其余为测试集测试模型的预测效果,识别结果如图13所示,混淆矩阵如图14所示。
图13 地层识别模型预测结果
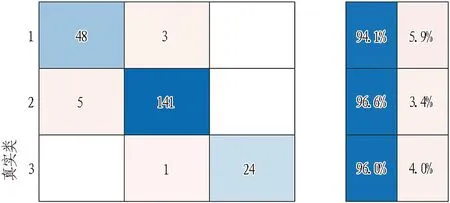
(a) 混淆矩阵 (b)模型召回率
通过混淆矩阵表明,预测为上软下硬地层的样本中90.6%确实为上软下硬地层; 预测为中风化泥质砂岩的样本中97.2%确实为中风化泥质砂岩; 预测为粉质黏土的样本中100%为粉质黏土。误差分析表明,实际为上软下硬地层的样本中,有5.9%被识别成中风化泥质砂岩,无样本被识别成粉质黏土; 实际为中风化泥质砂岩的样本中,3.4%被识别为上软下硬地层,无样本被识别为粉质黏土; 实际为粉质黏土的样本中,4.0%被识别为中风化泥质砂岩,无样本被识别成上软下硬地层。
预测结果表明,在该样本中,上软下硬地层的识别召回率为94.1%,中风化泥质砂岩识别召回率为96.6%,粉质黏土的识别召回率为96%,总体识别准确率为95%。因此,该模型能够实现掘进参数与开挖面不同地层之间的映射,且对单一地层识别准确率高,能够在掘进过程中识别所作业的地层。
5 复合比预测模型分析
通过地层分类,可以解决单一地层的识别问题。为了更准确地描述复合地层的复合情况,定义复合比φ表述地层复合情况并进行复合比预测,以提高ABC-BP神经网络模型对复合地层的预测能力。
针对施工区间内存在的地层复合情况,分别选取中强-中风化泥质砂岩与粉质黏土-中强风化泥质砂岩复合地层,进行复合比预测。以掘进参数刀盘转矩、刀盘转速、总推力、注浆量、注浆压力、掘进速度、土舱压力为作为地层识别模型的输入参数,以复合比作为输出参数。模型结构方面采用输入层、隐含层、输出层,神经元为7-15-1的结构; SVR模型惩罚系数取为3,径向基函数系数取为10; ELM模型隐含层节点数选为23。随机选取数据集中70%的数据为训练集,其余数据作为测试集,测试模型预测效果与精度。
ABC算法中设置最优参数: 蜂群大小为200,引领蜂和跟随蜂数量各为100,最大迭代次数为200,求解维度D为136,搜索空间范围Minj为-1、Maxj为1,单个蜜源最大开采次数为5。BP神经网络设置最优参数: 最大迭代次数为700,学习率为0.01,迭代精度为0.001。
5.1 强-中风化泥质砂岩复合地层预测分析
根据预测结果可知,强-中风化泥质砂岩段复合比神经网络预测值大部分与真实值接近,如图15所示。其中,红色曲线代表ABC-BP神经网络模型预测结果,黑色曲线代表复合比真实值。由图可知,在强-中风化泥质砂岩段,ABC-BP神经网络模型预测结果较其他机器学习模型预测结果的复合比与真实值更为贴合,也证明了ABC算法可以提高神经网络模型预测精度。
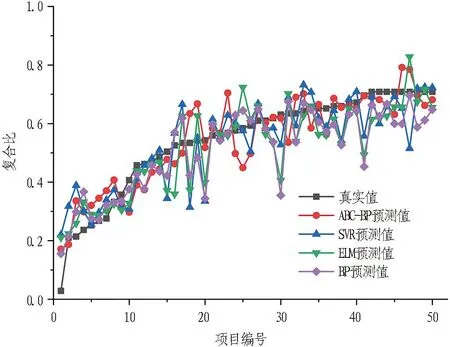
图15 强-中风化泥质砂岩段预测结果
ABC-BP神经网络模型与其他机器学习模型预测强—中风化泥质砂岩的评价指标统计结果如图16所示。由图可知,ABC-BP神经网络预测模型的平均绝对误差MAE为0.056,均方根误差RMSE为0.068,样本回归值R2为0.81; BP神经网络模型的平均绝对误差MAE为0.066,均方根误差RMSE为0.087,样本回归值R2为0.71; SVR模型的平均绝对误差MAE为0.066,均方根误差RMSE为0.087,样本回归值R2为0.72; ELM模型的平均绝对误差MAE为0.068,均方根误差RMSE为0.088,样本回归值R2为0.71。
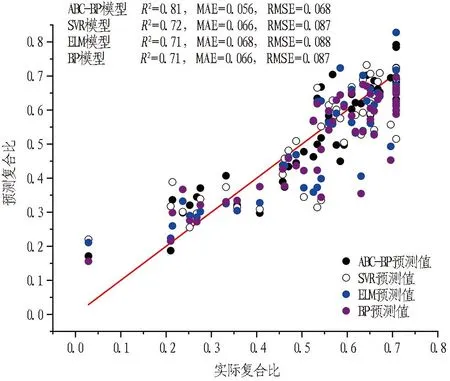
图16 强-中风化泥质砂岩段评价指标结果
ABC-BP神经网络模型的平均绝对误差和均方根误差均最小,样本回归值最大,证明在强-中风化泥质砂岩段,ABC算法优化使BP神经网络模型的预测精度和预测性能均得到了提升。
5.2 粉质黏土-强风化泥质砂岩预测分析
根据预测结果可知,针对粉质黏土-强风化泥质砂岩段复合比,ABC-BP神经网络模型预测值大部分与真实值接近,见图17。其中,红色曲线代表ABC-BP神经网络模型预测结果,黑色曲线代表复合比真实值。由图18可知,在粉质黏土-强风化泥质砂岩段ABC-BP神经网络模型的复合比预测结果较其他机器学习模型的预测结果更为准确,ABC算法有效提高了神经网络预测精度。
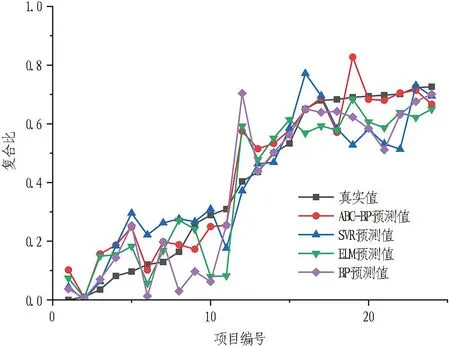
图17 粉质黏土-强风化泥质砂岩段复合比预测结果
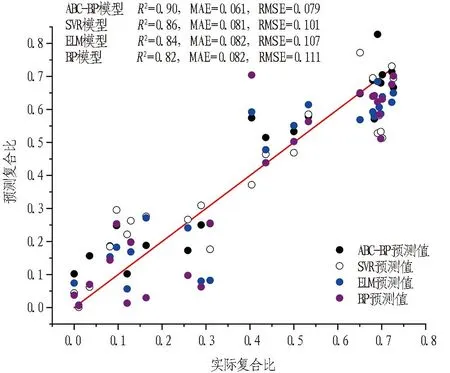
图18 粉质黏土-强风化泥质砂岩段评价指标结果
ABC-BP神经网络模型与其他机器学习模型预测粉质黏土-强风化泥质砂岩的评价指标统计结果见图18。由图可知,ABC-BP神经网络预测模型的平均绝对误差MAE为0.061,均方根误差RMSE为0.079,样本回归值R2为0.90; BP神经网络模型的平均绝对误差MAE为0.082,均方根误差RMSE为0.111,样本回归值R2为0.82; SVR模型的平均绝对误差MAE为0.081,均方根误差RMSE为0.101,样本回归值R2为0.86; ELM模型的平均绝对误差MAE为0.082,均方根误差RMSE为0.107,样本回归值R2为0.84。
ABC-BP神经网络模型的平均绝对误差和均方根误差均最小,样本回归值最大,证明在粉质黏土-强风化泥质砂岩段,ABC-BP神经网络模型性能仍有优越性。
6 结论与讨论
本文采用人工蜂群算法对BP神经网络进行优化,构建了地层识别模型与复合地层复合比预测模型,对南京地铁6号线某施工区间进行了预测,对比分析ABC-BP与SVR、ELM、BP模型的预测精度,探究盾构掘进参数与开挖面地层映射关系。
1)通过对盾构掘进系统各参数的统计分析,确定了3种地层下各掘进参数的特征: 上软下硬复合地层中呈现刀盘转速低、土舱压力高的特征;粉质黏土地层中呈现注浆量高、转矩低的特征;中风化泥质砂岩地层中呈现刀盘转矩大、土舱压力较小的特征。初步确定该区间机-岩之间的参数映射关系。3种地层中掘进参数的差异为利用掘进参数进行地层识别以及复合地层下复合情况预测提供依据。
2)基于机-岩关系,建立基于掘进参数的地层识别模型,对南京6号线某工区掘进参数与地层情况进行预测分析,结果显示地层识别模型对单一地层的识别准确率较高,均为95%以上; 对复合地层的预测准确率也达到了90%左右,提出的模型能够满足工程实践上地层预测精度的需要。
3)利用人工蜂群算法ABC优化BP神经网络模型,有效解决了BP神经网络模型训练过程中容易陷入局部最小值问题,提高了预测的精度,且预测能力优于其他机器学习模型。ABC-BP模型与BP模型所预测的复合比结果对比表明,ABC-BP预测结果中平均绝对误差MAE减小了0.01~0.021、均方根误差RMSE减小了0.019~0.032,且样本回归值R2较BP模型增加了0.08~0.10。经人工蜂群算法优化后的模型误差更小且拟合精度更高。
4)在本工区的2种复合地层区间,使用ABC-BP模型预测地层情况,具有一定的准确性,能满足现场施工要求。本文所述ABC-BP模型建立起的机-岩关系,可用于开挖过程中的地层实时在线监测与识别,可为及时根据开挖面调整盾构掘进参数提供参考。
在后续研究中,可以考虑将复合比预测与现有的掘进参数预测方法相融合,建立一种更为全面的掘进过程中参数预测模型。通过综合考虑复合比的影响,该模型能够更准确地预测掘进过程中各种参数的变化趋势,提高掘进操作的精确性和效率。该方法同样可以应用于沉降预测的神经网络模型中,补充输入参数,通过引入复合比预测,可以更全面地考虑地质条件对沉降的影响,提高沉降预测模型的准确性。
