顾及基准点误差的自由设站平差及精度分析

刘琼琼，闫广峰

（1. 周口市规划建筑勘测设计院，河南 周口 466000；2. 内江师范学院地理与资源科学学院，四川 内江 641100）

自由设站法是目前测量实践中，利用全站仪进行地形图测量、施工放样、变形监测等测量工作的常用方法，其具有设站位置选择灵活、工效高、精度高、控制点间不要求通视等优点。国内外学者围绕自由设站方法开展了大量的基础理论和应用研究[1-5]。目前进行自由设站的数据处理时，通常采用经典约束平差法，其以所有联测的基准点为固定点、所有水平方向和水平距离测量值为观测值，并以设站点坐标和定向角为待求参数进行求解。然而，由于测量误差、平差模型等因素的影响，自由设站采用的基准点坐标会含有误差，测站约束平差后其会以原始数据误差[6]的形式影响设站点坐标和定向角估值，进而影响碎部点坐标。特别当基准点精度较低时，这种不利的影响将更为显著。为此，本文在分析自由设站基本原理基础上，基于部分变量误差（partial errors-in-variables，Partial EIV） 模型平差理论和方法，以新的思路解决自由设站平差问题。

1 全站仪自由设站基本原理

全站仪自由设站外业观测如图1 所示，其中，P为设站点，A～E为基准点（不少于2个），P1和P2为待测量碎部点。

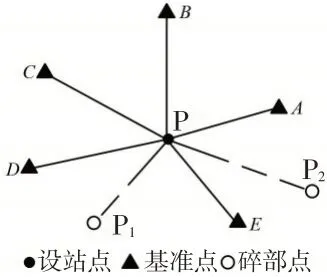
图1 全站仪自由设站外业观测示意图

目前进行自由设站测量数据处理时，将P 点坐标XP、YP和测站的定向角φ作为待求参数，P 点观测A～E 点的水平方向测量值LA～LE、距离测量值SA～SE为观测值，A～E点坐标XA、YA...XE、YE为固定值，由此建立自由设站平差问题的数学模型。

1）函数模型：

2）随机模型：

式中，ΔφP为定向角改正数；为点P 的近似坐标改正数；为点P 和点i 的近似坐标较差；ρ″=206265 为常数；LPi和分别为Pi 的方向观测值和近似方向值；SPi和分别为Pi的距离观测值和近似距离值；D为观测值的协方差阵；σ0为先验单位权中误差；Q为观测值协因数阵；P为观测值的权阵，可按照经验定权法并结合仪器标称精度确定。

根据最小二乘原理，由式（1）求解参数XP、YP、φ的估值̂，再由P 点观测碎部点P1、P2的水平方向和水平距离观测值L1、L2、S1、S2，根据极坐标原理可得到P1、P2点的坐标：

式中，Xi、Yi为第i个碎部点坐标，i=1,2。

由原始数据误差理论[6]可知，以上基于经典约束平差方法进行自由设站数据处理，平差前后的基准点坐标不变，基准点误差会以原始数据误差的形式影响设站点坐标、测站定向角估值，并进一步传递至碎部点坐标。当设站采用的基准点精度较低时，原始数据误差给自由设站精度带来的不利影响不容忽视。

为解决经典约束平差模型难以顾及自由设站基准点误差的问题，本文探索以新的思路解决自由设站数据处理问题。注意到图1中，若以P为坐标系原点，P观测基准点A的方向PA为x轴，x轴顺时针旋转90°方向为y 轴，建立平面直角坐标系，则根据P 点观测的水平方向、水平距离观测值可求得基准点、碎部点在该站心坐标系的平面坐标。由基准点在站心坐标系、测量坐标系下的2 套坐标，可建立基准点两套坐标间的坐标转换平差模型，若建立的模型能够准确表达2个坐标系之间的相对空间位置关系，便可根据求得的模型转换参数求解得到设站点和碎部点在测量坐标系的坐标。

2 顾及基准点误差的自由设站平差模型

以设站点P 为坐标系原点，P 点至联测的任一基准点方向为X轴，X轴顺时针旋转90°方向为Y轴，建立站心坐标系。根据P至各基准点和碎部点的水平方向、水平距离观测值，可求得基准点、碎部点的站心坐标系坐标。要进一步得到设站点和碎部点的测量坐标系下坐标，必须找到站心坐标系和测量坐标系间的相对空间位置关系。为此，基于基准点在站心坐标和测量坐标系下的2 套坐标，建立2 个坐标系间的坐标转换模型。

由于基准点的建网测量与自由设站测量时可能采用不同的技术手段，因此，2 个坐标系之间可能会存在一定的尺度差异。为此，建立能够完整表达站心坐标系与测量坐标系之间存在的平移、旋转和尺度差异关系的相似变换坐标转换模型[7-8]：

式中，和分别为第i个基准点的测量坐标系坐标和站心坐标系坐标，i=1,2,...,n；X0、Y0为平移参数；m为尺度因子；α为旋转角。

令Z1=mcosα、Z2=msinα，并设

则式（4）可表示为线性模型：

式（5）的系数矩阵A由常数0、1以及基准点的站心坐标构成。进一步考虑式（5）中的基准点站心坐标误差，可得坐标转换Partial EIV模型

式中，为系数矩阵A的真值矩阵；el为l 对应的随机误差向量；EA为A对应的改正数矩阵，其固定值对应部分为0，相同随机元素对应的改正数相同。

将式（6）看作非线性Gauss-Helmert 模型[9]，并将EA中随机量作为待求参数，则式（6）可表示为：

式中，为a的真值向量；EA为系数矩阵A对应的改正数矩阵；观测值为 ；待求参数为。

采用高斯-牛顿法迭代方法对式（7）求解[9]。设第i 次迭代后，参数X的估值为X(i)，eAs的估值为eAs(i)，将式（7）右端在()X(i)，eAs(i)处用泰勒级数展开并取至一阶项

式中，δX为X(i)的微小改正值；R为与X(i)、EA的有关的矩阵，满足ReAs=EAX(i)。

以式（9）为目标函数：

对各变量求偏导且令导数等于0，可得：

以参数的最小二乘解为初值，根据式（10）、式（11）进行迭代计算，直至<ε （ε 为小的常数）时迭代结束。由此得到测量坐标系和站心坐标系之间的坐标转换参数估值和。

进一步计算尺度因子m、旋转角α的平差值：

式中，arctan(x)为对x求反正切。

则设站点、碎部点在测量坐标系下的坐标为：

从以上自由设站数据处理过程可以看出，相较于经典的约束平差法，所建立的平差模型，给系数矩阵引入误差向量，考虑了观测误差对自由设站平差的影响；以基准点的测量坐标系坐标为观测值，能够顾及到基准点误差的影响。为叙述方便，称以上方法为顾及基准点误差的自由设站平差法（free stationing adjustment considering the datum point errors， 简称FSA-CDPE）。

3 实验设计与结果分析

为了评估FSA-CDPE方法进行自由设站数据处理的可行性和有效性，基于某建筑工程的放样测量实际，设计全站仪自由设站仿真实验。外业观测如图2所示，采用自由设站方法进行碎部点放样，其中，A～D为基准点，P 为设站点，P1和P2为待测量碎部点。

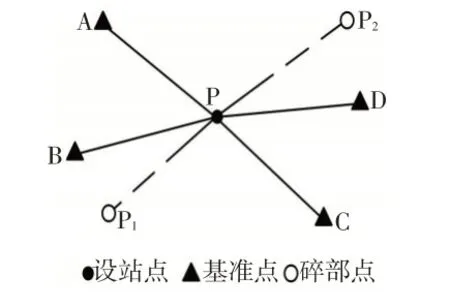
图2 全站仪自由设站法测量

设站点P 至各基准点、碎部点的方位角和距离为方向、距离观测值模拟真值，分别如表1、2所示。

表1 各点测量坐标系的坐标真值

表2 观测值模拟真值

利用随机数发生器，首先给P 至各基准点、碎部点的观测值添加观测误差，其中，添加的方向观测值中误差为±1.0″ ，距离观测值固定误差为±1.0 mm、比例误差为±1.5 ppm，各基准点、碎部点均观测2 个测回。再往基准点A～D的X、Y的坐标中分别添加5种不同中误差σ大小的正态分布随机误差，具体方案为：①u=0、σ=1.0 mm；②u=0、σ=2.0 mm；③u=0、σ=3.0mm；④u=0、σ=4.0mm；⑤u=0、σ=5.0mm。

分别采用经典约束平差法、FSA-CDPE 法进行自由设站平差，并用平差后的设站点和碎部点坐标真误差平方和M评定平差结果的整体准确度（M 越小，自由设站平差结果准确度越高），用点位真误差TP衡量设站点和碎部点的平差结果准确度。

设碎部点和设站点个数共计为k，M可采用下式求解：

式中，为碎部点或设站点的平差值；、为碎部点或设站点的真值。

TP的计算公式为：

5种方案的实验结果如表3所示。

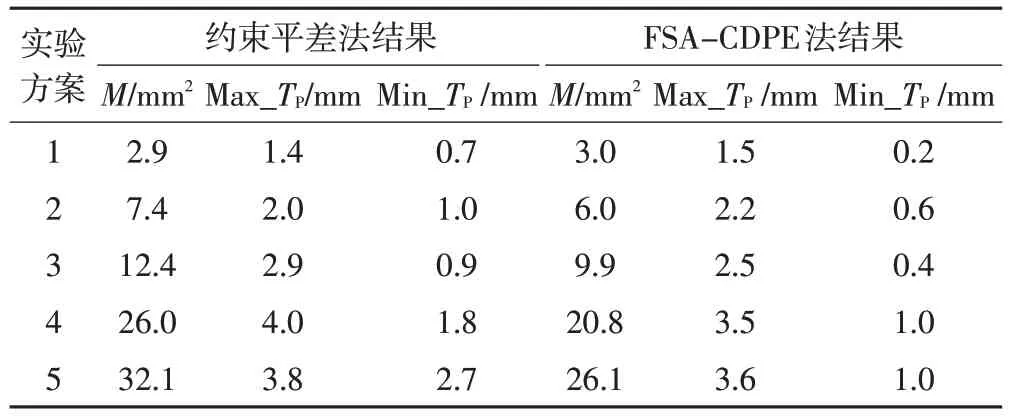
表3 各实验方案结果

表3 中，Max_TP、Min_TP分别为平差后设站点、碎部点的点位真误差最大值和最小值。从表3 的实验结果可以看出，无论是采用约束平差法还是FSA-CDPE 法，随着给基准点坐标添加误差值的变大，坐标真误差平方和M逐渐变大，设站点和碎部点的点位真误差也呈增大趋势。此外，还可以发现，当给基准点添加的误差较小时，采用约束平差方法和FSA-CDPE 方法的自由设站平差结果相当，如方案1、2 中，2 种方法的坐标真误差平方和M 和点位真误差均相差较小；随着往基准点中添加误差量级变大，2 种方法的平差效果差异明显，如方案5 中，约束平差结果的坐标真误差平差和M为32.1、最大和最小点位真误差为3.8 和2.7，而FSA-CDPE 方法的M 值为26.1、点位真误差最大值3.6、最小值1.0。

通过以上分析可以得出，较大的基准点误差会给自由设站平差结果的精确度带来不利影响；FSA-CDPE 方法用于自由设站数据处理是可行且有效的，当基准点精度较高时，其与经典约束平差方法结果相当；但当基准点精度较低时，其平差结果较约束平差方法更优。

4 结语

通过初步的理论和实验分析，可以得到以下结论：

1）进行自由设站数据处理时，应兼顾基准点误差的影响。否则当基准点误差较大时，其会给平差结果带来较大的不利影响。

2）FSA-CDPE方法与经典约束平差法进行自由设站数据处理，当基准点的精度较高时，2 种方法的结果相当；基准点精度较低时，前种方法较后种方法得到的结果更优。

3）FSA-CDPE方法用于自由设站数据处理是可行且有效的，其平差模型同时考虑了全站仪测量误差和基准点误差的影响，理论上是严密的，为全站仪自由设站数据处理提供了一种新的思路和有效方法。