基于遗传优化聚类的GRU 无损电力监测数据压缩
2024-05-07屈志坚帅诚鹏吴广龙梁家敏
屈志坚,帅诚鹏,吴广龙,梁家敏,李 迪
(1.华东交通大学轨道交通基础设施性能监测与保障国家重点实验室,南昌 330013;2.华东交通大学电气与自动化工程学院,南昌 330013)
在现代配电自动化系统中,利用互联网、人工智能等技术,围绕电力的各个环节实现配电网的数字化和智能化,使其具有全面感知、传输、高效处理和报警信息、便捷灵活应用等特点[1]。属于处理层的电网调度中心[2],其数据量随着现场设备种类和数量的不断增加而呈现出不断攀升的态势,并以极其庞大的数量、规模和结构生成电力大数据[3]。电力数据主要分为3 个类型:第1 类是电网运行中设备监测数据,如监视控制与数据采集数据和智能电表的采样数据;第2 类是包括成交价数据、售电量数据在内的电力营销数据;第3类是内部电网数据等电力管理数据。目前学术界和工业界在针对千万级的数据时,推荐分布式集群方式处理[4],但随着数据体量增大会出现集群内存资源不足,传输效率降低,数据查询时间增大等问题。
因此,学术领域的研究学者针对优化集群内存结构,减少磁盘储存空间等问题展开了一系列研究[5-7]。文献[8]以Gzip 压缩算法为蓝本,同时采用LZ77压缩算法与霍夫曼编码,设计了专用的硬件电路,实现了无损压缩,提高了数据的压缩速率,但数据的压缩率依赖于硬件的性能。LZMA 是用LZ77字典编码改良和优化后的压缩算法,文献[9]利用开源的LZMA 代码进行系统移植,将LZMA 算法代码封装嵌入数据库系统,将数据先进行压缩,再传输至数据库;文献[10]提出一种基于深度学习的上下文自适应压缩DeepCABAC(context-adaptive binary arithmetic coding for deep neural network compression),利用上下文匹配算法生成预测概率分布表,再将概率分布表输入深度学习进行优化,但由于使用的上下文匹配算法比较依赖先验数据的初始概率分布,仍很难满足电网监测数据压缩率的需求。随着神经网络算法的出现,人们开始将神经网络的自主性特征学习功能应用于信息处理领域,文献[11]通过神经网络模型对大量样本数据进行训练,将循环神经网络RNN(recurrent neural network)模型构建为序列数据的条件预测概率,并对字符的概率分布进行更新和优化,采用基于预测的无损数据压缩原理,数据压缩效果得到有效提升。但是,RNN 在处理长期依赖和计算距离比较远的节点之间的联系时,因为雅可比矩阵的多次相乘会造成梯度消失或梯度膨胀的现象,而本文提出的门控循环单元GRU(gated recurrent unit)神经网络则能很好地解决这一问题。
另一方面,由于电网系统数据信息的复杂性,在数据压缩之前对数据信息进行聚类预处理也可以有效地提高数据压缩率。文献[12-13]比较了多种传统的聚类算法,对于进行聚类之前需要预先给定聚类中心数的K-means 算法来说,如果集群所有数据信息文件,不能确切地给出聚类中心,往往会造成不理想的聚类输出结果。因此,文献[14]根据密度峰值算法思想,对K-means 算法的距离和权重参数进行改进,引入了加权欧式距离,得到了较好的聚类结果。但是权值的分配还需要引入进化算法对其进一步优化。
为此,本文提出一种遗传聚类优化的门控循环单元神经网络GA-K-GRU(genetic algorithm optimizing K-clustering gated recurrent unit neural network)数据压缩方法。先将分布式平台集群的多维原始电力数据进行聚类,并通过遗传算法迭代优化聚类中心的选取,再利用GA-K-GRU 的历史参数记录功能训练输出数据的概率分布模型,最后结合算术编码将其编码压缩存储至集群。实验结果表明,本文方法的压缩效果比LZMA、Gzip、DeepCABAC、RNN 等压缩算法效果更好,有效缓解了集群存储空间,提高了集群存储速度,提升了集群查询时间。
1 基于分布式平台的集群压缩模型设计
1.1 分布式集群实验环境
在Ubuntu 18.04 系统环境下,按工程中典型调度主站2 台数据服务器和2 台主、备调度工作站4机配置,建立由1台主调度机,2台监控服务器,1台备调度机构成的4机分布式集群实验环境,其配置如表1所示。
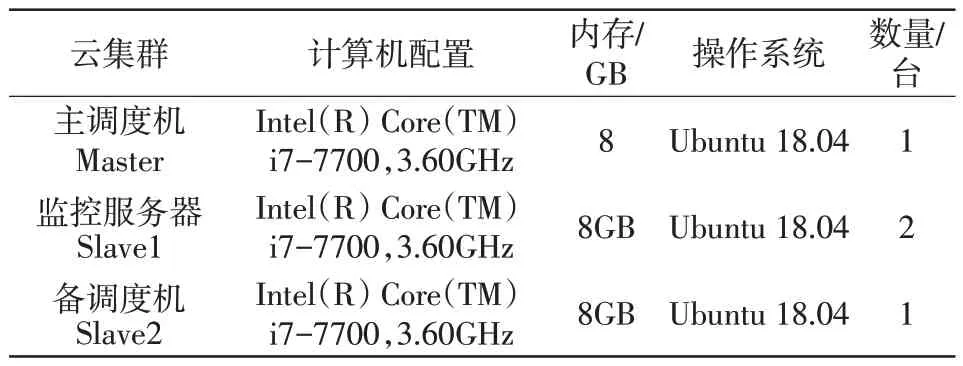
表1 分布式集群实验环境Tab.1 Distributed cluster experimental environment
1.2 分布式集群无损压缩设计
电网监测数据分布式集群的数据处理任务包括Map和Reduce两个进程,分布式集群为Map/Reduce任务处理提供多种数据压缩格式的压缩接口[15]。
输入分布式集群中的数据文件被分割为若干个数据块(Data1,Data2,…,Datam) ,各数据块通过Map 任务以并行方式映射至分布式集群的任务监视节点,各节点处理后的数据以文件流的形式输出至集群进行储存,在Reduce 任务中进行排序与聚合,集群压缩流程如图1所示。
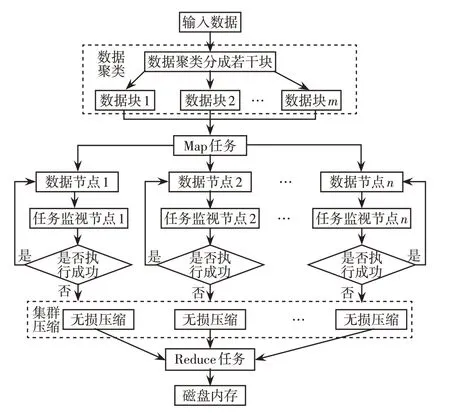
图1 集群压缩流程Fig.1 Cluster compression process
在处理传输电网监测数据文件的过程中,先对输入的数据信息文件进行数据聚类处理,将文件聚类分成m个数据块,再通过Map进程将m个数据块并行运行在4台集群中,分别对各个数据块节点进行无损压缩处理减少数据体量,最后将压缩后的数据块通过Reduce 进程汇总存储至磁盘,缓解磁盘存储压力。
2 遗传优化的电力监测数据聚类设计
由于K-means 聚类只是以数据文件中数据点到聚类中心的距离最小进行分类,而这个聚类中心个数(即K值)是人根据经验设定,往往不是最优的聚类中心个数。而利用遗传优化算法可以对不同K值的聚类效果构建适应度函数,通过不断的迭代对K值进行寻优,最后输出最优的聚类中心数。具体寻优过程如下。
1)可变长度字符染色体编码
假设电力监测数据集V进行聚类后,每个聚类XM×N中总共有N个元素,每一个元素xi的维数为M,则可用向量={d1,d2,…,dn}表示,其中1 ≤i≤N。设种群大小为Qi,种群中的每一个个体都代表一种聚类方法,将个体表示为,其中1 ≤k≤Qi,这表示该个体有k个聚类中心,每个聚类中心的坐标用xˉc表示,1 ≤c≤k。
因为最佳的聚类中心数K不确定,因此个体编码长度都是可变的,将种群中的每个个体编码为可变长字符串,给种群中的聚类中心数目设置一个取值范围Cmin≤k≤Cmax,然后将种群编码为{V1,V2,…,Vj,…,VQ}。
2)适应度函数选择
一般的K-means 算法将每个数据点到其对应的聚类中心的距离之和作为优化指标,并没有考虑聚类中心之间的距离问题,导致聚类中心会受到孤立点影响的情况,所以本文选择戴维斯-布尔丁指数DBI(Davies-Bouldin index)[16]作为衡量聚类效果的适应度函数。
DBI表示聚类中数据点之间的距离与聚类中心之间距离之比的平均值。DBI 的值越小,表示聚类后簇内距离越小,簇之间的距离越大。在迭代中通过消除具有较大DBI值的个体,可以维持种群的规模,并且会尽可能多地包含“精英”个体,从而可以加快最佳解决方案的速度。
3)交叉算子
交叉算子通过交换上一代个体的遗传信息来产生新的子个体,从而扩大了问题解决领域的搜索范围。
交叉过程如图2 所示,随机从群体中选择2 个个体父代1、父代2 进行交叉,产生2 个新的个体子代1、子代2,重复进行直到产生Qc个新个体。

图2 交叉过程Fig.2 Cross process
4)变异算子
变异算子通过修饰个体的某些染色体片段来维持个体的多样性,从而解决局部最优的问题。在每个变异操作中,以概率Pn突变当前种群的个体Vx,直到产生Qn个新个体,并根据以下策略修改聚类中心的数量:如果聚类中心的数量大于(Cmin+Cmax)/2,随机删除1 个聚类中心;否则,随机生成1个聚类中心。
5)个体消除策略
经过种群初始化、个体交叉及变异操作之后,种群生成了Qi+Qc+Qn个个体。经过交叉和变异,会产生相同序列或不同序列但具有相同染色体个数的个体,即相同聚类中心的个体。这些个体再次迭代会导致早期收敛到局部最优的问题。因此有必要比较相同长度的染色体用来除去多余的个体。最后根据DBI计算适应度,按照适应度进行总体排序,并消除具有较大DBI 值的个体,从而使种群的总体规模保持不变。
遗传优化K-means聚类算法在最优K值的适应度达到给定阈值、最优K值的适应度不再提高或算法的迭代次数达到预设值时终止,然后输出优化后K个聚类的数据文件。
任意的数据文件均可以看作是字母表中的一串字符,压缩电力数据文件包含2个阶段,需遍历2次数据文件,第1次依据输入的数据输出概率分布模型,第2次将生成的概率分布模型与编码器结合来制作压缩文件。信息熵公式为
式中:H(U)为输入全部数据压缩后的数据大小;h(xi)为文件中每个数据的压缩大小;P(xi)为每个数据出现的概率。
根据式(1)可知,电力监测数据集中数据的相关性越高,其高频数据压缩后占用的字节数越少,有利于缓解存储和数据传输的压力。利用皮尔逊系数对数据进行相关性验证,得出相关性热力表,验证结果如图3所示。
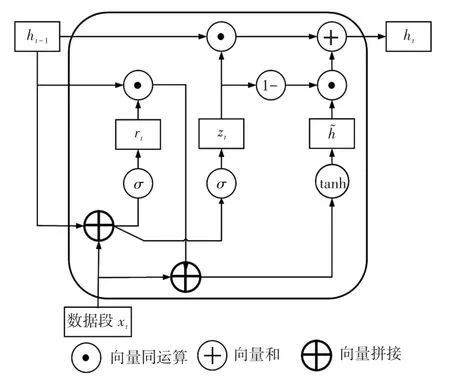
图3 GRU 结构Fig.3 Gated recurrent unit structure
3 RNN 概率分布模型
3.1 GRU 神经网络模型架构
对于给定的一组数据信息,RNN对其输入序列进行建模,输出数据的字符概率分布模型,并循环更新其隐藏状态,但循环神经网络存在的梯度消失或爆炸会导致同一组信息前后的关联性减弱等问题,而GRU 神经网络通过引入更新门和重置门可以很好地解决梯度消失或爆炸的问题。其中更新门决定保留多少数据历史信息,添加多少新的数据信息;重置门控制过去的数据信息对待输入数据信息的贡献。单元重置和更新信息的公式为
式中:xt为t时刻输入的数据段;zt、rt分别为数据段xt的更新门和重置门;是t时刻的候选状态;ht为t时刻网络隐藏层的输出;Wz、Wr、Wh和Uz、Ur、Uh为权重参数;bz、br、bh为偏置参数。
GRU结构如图3所示,GRU可以通过更新门机制更好地传递相隔距离较大的2 个数据段之间的依赖关系。当训练基于GA-K-GRU 结构的电力监测数据集的概率分布模型时,GA-K-GRU有多个自由定义的参数,包括隐藏层层数、隐藏层单元个数以及单个神经元输入的数据段大小等,GRU的具体参数如表2所示。

表2 GRU 参数Tab.2 GRU parameters
3.2 电力监测数据GRU 压缩模型
为了训练GA-K-GRU 结构的电力监测数据集的概率分布模型,将电力监测数据集分段,输入GRU 神经网络输入端,利用GRU 神经网络隐藏层中状态量的传递性,训练电力监测数据输出的每个字符与其对应的字符概率分布表。通过该方法得出的整体性字符概率分布表将更为准确,使出现频繁的字符对应的概率更高,压缩后所占字节数更少,从而提高整体压缩率,建模过程如图4所示。

图4 GRU 的概率分布建模流程Fig.4 Flow chart of probability distribution modeling of GRU
数据压缩流程如图5 所示,以电网监测数据中字段“Ua220V50HzUa221V50HzUa210V50Hz”为例说明字符概率分布表训练流程。将电网监测数据中字段输入GRU 模型,并分解为3 个数据段x1=“Ua220V50Hz” 、x2=“Ua221V50Hz” 、x3=“Ua210V50Hz”;首先,计算数据段x1中字符的概率分布,输出概率分布{U:0.1,a:0.1,2:0.2,0:0.2,V:0.1,5:0.1,H:0.1,z:0.1};再将数据段x1的概率分布作为隐藏层信息h1传递至数据段x2,综合h1与x2得出数据段x2的概率分布{U:0.1,a:0.1,2:0.2,0:0.15,V:0.1,5:0.1,H:0.1,z:0.1,1:0.05};最后,将数据段x2的概率分布作为隐藏层信息h2传递至数据段x3,最终模型输出的字符概率分布为{U:0.1,a:0.1,2:0.17,0:0.17,V:0.1,5:0.1,H:0.1,z:0.1,1:0.06}。

图5 电力监测数据分段压缩流程Fig.5 Segment compression processof power monitoring data
利用GRU 模型训练生成的字符概率分布,结合算术编码对电网检测数据进行压缩处理。如图6所示,输入电力数据集中字符串“Ua220V50Hz”,通过GRU 神经网络训练地生成概率分布:{U:0.1,a:0.1,2:0.2,0:0.2,V:0.1,5:0.1,H:0.1,z:0.1}。

图6 电网监测数据的算术编码Fig.6 Arithmetic coding of power grid monitoring data
当字符串“Ua220”输入时,第1 个字符为U,则标记位于区间[0.0,0.1)中,此时丢弃除此区间以外的其他部分,并按原区间比例继续划分;第2 个输入字符为a,标记落在区间[0.01,0.02)中;继续划分第3 个字符,2 落在区间[0.012,0.014)中;第4 个字符2 落在区间[0.012 4,0.012 8)中;最后一个字符0定位于区间[0.012 56,0.012 64)中;区间[0.012 56,0.012 64)内任意一个浮点数,比如0.01262,可以表示字符串“Ua220”。
通过算术编码方法处理,对于任意字符串,结合GRU 模型输出的字符概率分布,都可以压缩为一个浮点数;数据的解码则是上述过程的逆过程。图7为有功功率数据压缩与解压后的数据对比,可以看出,原始数据与解压数据的波形完全吻合。由此可知,本文的GRU压缩为无损压缩。

图7 无损压缩性能验证Fig.7 Verification of lossless compression performance
4 算例测试
4.1 数据准备
本研究算例测试数据来源于3 个电力监测数据集:荷兰能源数据集DRED(Dutch residential energy dataset)[17]、英国电器级电力数据集UK-DALE(UK domestic appliance-level electricity)[18]和雨林电力采集自动化数据集RAE(rainforest automation energy)[19],如表3所示。

表3 算例测试的电力监测数据集Tab.3 Power monitoring datasets for example test
4.2 遗传优化K-means 聚类的实验验证
本文基于可变长度染色体编码的遗传算法,在迭代过程中对K-means聚类算法的聚类中心数目K值进行寻优。遗传算法参数设置:初始交叉概率Pc=0.7,初始变异概率Pv=0.04 ,最大迭代次数I=2 000,初始聚类中心数K值设为20。
为验证遗传优化K-means 聚类压缩效果,将未遗传优化的K-means聚类与进行遗传优化K-means聚类对D4 数据集进行压缩对比测试,压缩率计算式为
式中:F1为电网检测数据文件压缩之后的大小;F2为电网检测数据文件压缩之后的大小。压缩率对比测试结果如图8所示。

图8 遗传优化K 聚类与K 聚类压缩对比Fig.8 Comparison of compression between genetic optimization K-clustering and K-clustering
由图8 可知,聚类数K=3 时压缩率最低,且经过遗传优化K-means 聚类的压缩率比未经过遗传算法优化的压缩率更低。这是因为遗传算法在对K值优化迭代的过程中不仅在寻找最优的聚类中心数,而且也在优化对每个聚类中心点位置的选取,所以本文利用遗传算法优化聚类中心的数目和位置都是最优,提高了数据文件的聚类效果。
为验证不同聚类算法下的压缩性能比较,本文将遗传优化K-means 算法与用遗传优化算法优化聚类中心后的K-medoids 聚类、层次聚类和密度聚类3种聚类方法对数据集D1~D9进行压缩对比,压缩结果如表4和图9所示。

图9 4 种聚类的压缩对比Fig.9 Comparison of compression among four clustering algorithms
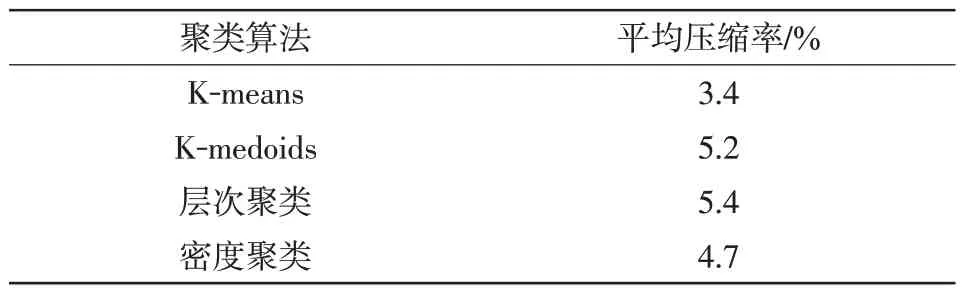
表4 不同聚类算法平均压缩率对比Tab.4 Comparison of average compression ratio among different clustering algorithms
从遗传算法的原理可知,其优化的只是不同聚类算法的聚类中心数,以及对聚类中心点位置的选取,但是由于不同聚类算法本身对于聚类中心选择的标准不同,所以优化后的效果也不同。由压缩率测试结果可知,遗传算法优化效果最好的是Kmeans聚类。
4.3 GA-K-GRU 算法压缩效果对比
为验证本文算法的压缩效果,分别使用GRU、RNN[11]、DeepCABAC[10]、Gzip[8]、LZMA[9]5 种数据压缩算法对表1 中的9 个数据集压缩,计算压缩率。对比测试结果如图10所示,图10(a)为数据文件没有进行遗传聚类优化的压缩测试结果,图10(b)为进行遗传聚类优化后的压缩测试结果。
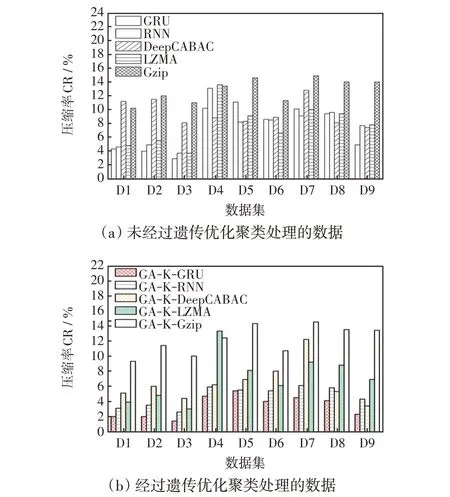
图10 5 种算法的压缩对比Fig.10 Comparison of compression among five algorithms
从图10 可以看出,对每一个数据集,无论在聚类与未聚类情况下,GRU的压缩率均低于其他4种压缩算法。这是因为对于同样的数据信息,通过GRU 模型训练输出字符概率分布结合算术编码更加接近信息熵,赋予数据信息中频率高的字符更高的字符概率,减少了编码字节数。
计算图10中9个数据集的平均压缩率,记录于表5。由表5 可知,经过聚类处理的数据再输入压缩算法进行压缩后,整体数据压缩率都有降低,但仍然是GA-K-GRU的压缩率较其他4种更低。这是因为GA-K-GRU 算法是先对数据进行遗传聚类处理,数据聚类后可增加同一个聚类文件中数据的相似度,再通过门控循环神经网络生成概率分布模型,使得高频出现的数据所占字节数更少,大幅提高了电力监测数据无损压缩的效果。
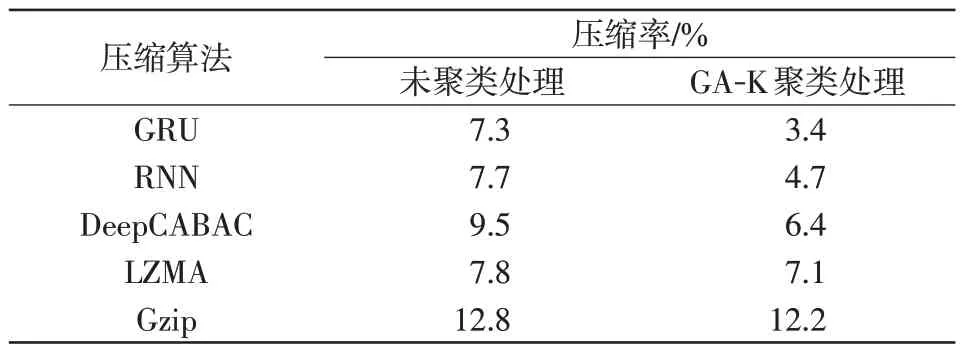
表5 聚类和未聚类的5 种压缩算法的平均压缩率对比Tab.5 Comparison of average compression ratio among five clustered and unclustered compression algorithms
5.4 不同压缩算法集群性能对比测试
为验证本文压缩算法对集群性能的影响,在搭建的分布式平台集群下,通过对5种压缩算法与原始集群共6种实验条件进行集群存储空间、存储速度及查询性能3个指标进行对比测试。其中,集群内存占用空间是指数据集压缩前后所占集群内存空间的大小;集群存储速度是指数据压缩前后导入同一个数据集所需要的时间;集群查询时间是指数据压缩前后对集群数据进行查询查询所消耗的时间。
存储空间对比结果如图11 所示。通过上述测试结果可以看出,数据在存储前通过GA-K-GRU方法进行压缩存储后,集群磁盘的内存空间得到了极大的提升,占用减少了约96%左右。说明本文的GRU 压缩算法非常有效地节约了电力数据的内存空间占用问题。
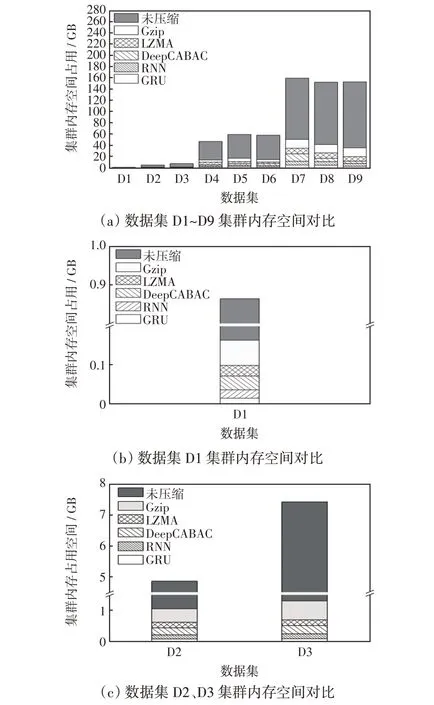
图11 集群内存空间对比Fig.11 Comparison of cluster memory space
集群存储速度如图12 所示。从测试结果可以看出,数据集经本文设计的压缩算法压缩后,存储速度平均提升约27%。这是因为压缩后的数据更加整齐。

图12 集群存储速度对比Fig.12 Comparison of cluster storage speed
集群查询时间对比如图13 所示,从测试结果可以看出,本文压缩算法使集群的查询性能也有所提升,平均节约27%左右的查询时间。

图13 集群查询时间对比Fig.13 Comparison of cluster query time
6 结 论
针对电力调度中心数据堆积越来越大的问题,结合数据聚类和神经网络中的概率模型优化,提出了一种GA-K-GRU压缩方法,通过对比实验分析得出以下结论。
(1)遗传优化K聚类算法可以很好地改善数据写入神经网络时属性分散的问题,对体量较大、结构较为复杂的电力数据有比较好的聚类效果,GAK-GRU 比经过遗传优化K 聚类后的Gzip、LZMA、DeepCABAC 和RNN 算法平均压缩率分别低8.8%、3.7%、3.0%和1.3%,可以较好地缓解电网监测数据的传输压力。
(2)以电力监测数据集为算例,搭建Hadoop 分布式集群平台,进行多组不同压缩算法下的集群性能对比。结果表明,本文设计的遗传优化聚类门控神经网络压缩可以减少约96%集群内存空间占用,提高约27%集群数据存储速度,提升27%集群数据查询时间,均优于主流的LZ系列和自适应压缩算法。
本文通过GA-K-GRU方法,提高了集群数据的压缩效果,可以有效缓解集群空间压力,但本文算法会占用较高的CPU资源,后续的研究重点会放在减少计算机资源占用上。
