大直径螺旋埋弧焊管弯曲变形能力的模拟研究

方 伟，陈心怡，吕 华 编译

（中国石油集团工程材料研究院有限公司，西安 710077）

0 前 言

钢管的弯曲变形能力对于建设期和运行期管线的结构完整性非常重要。在易于沉降的土壤中由采矿、地震或冻土解冻引起的土壤沉降，导致陆上埋地管线承受较大的弯曲载荷。此外，管线的定向钻进和穿越活动的构造断层会使管线产生较大的弯曲变形，山体滑坡或横移等地质灾害也会导致埋地管线承受较大的弯曲载荷。

钢的材料性能和径厚比D/t都会对钢管的弯曲响应造成影响。钢管在塑性区的弯曲响应最初表现为钢管横截面的椭圆化，称为“Brazier 效应”。在弯曲载荷持续作用下，钢管横截面两极位置发生塑性变形，并且弯管内弧侧压缩应变增大。内弧侧压缩变形到一定程度，可使管壁起皱而发生结构性失稳，导致钢管失效。与结构性应用相比，管线用钢管的极限弯矩值可以忽略，而钢管的变形能力却是设计中的重要参数。

对于典型结构钢制造的D/t为60～120的薄壁钢管，通常在达到极限弯矩之前就发生起皱和屈曲，这与Brazier效应一致。此外，屈曲的发生非常突然（管壁越薄，屈曲就越突然），其特征是短波长起皱。钢管起皱后很快在局部扭结，从而失去结构强度。

螺旋缝埋弧焊工艺（SAWH）为生产薄壁管线管提供了一种经济有效的方法。现有的管线设计体系可能不支持在管线应用中采用螺旋埋弧焊管，在这种情况下，基于应变设计十分必要。管道行业普遍认为在相同的载荷条件下，螺旋埋弧焊管的力学性能与无缝管和直缝焊管（包括直缝埋弧焊、高频焊、电阻焊管）不同，且现行的设计规范可能不适用于螺旋埋弧焊管，尤其是对于海上应用。然而，最近螺旋埋弧焊管逐渐成为了几条管道的备选方案，螺旋埋弧焊管的弯曲能力是保障管道建设期和运行期结构完整性的重点。

本研究的目的是研究螺旋埋弧焊管在承受弯曲应力时的结构响应和屈曲变形，并确定其变形极限。以全尺寸试样试验数据为基础，采用有限元模拟工具，对钢管变形能力进行数值模拟并通过试验结果进行验证。分析考虑了材料性能和初始几何缺欠等因素。此外，在采用单独的数值模型模拟钢带在螺旋埋弧焊管生产过程中的冷弯过程时，还考虑了残余应力因素。基于以上有关材料性能、初始缺欠和残余应力等信息，采用经验证的有限元模型研究不同几何参数和材料参数条件下螺旋埋弧焊管弯曲响应的敏感性。最后，将分析结果与现有的基于应变设计的管线设计规范进行了比较。

1 钢管试样和初始参数测量

本研究采用两根螺旋埋弧焊管（1#管和2#管），1#管名义外径和壁厚分别为1 067 mm 和15.9 mm，实测外径和壁厚分别为1 065.62 mm和16.375 mm，因此实际的径厚比（D/t）为65.1；2#号管名义外径和壁厚分别为1 067 mm 和9 mm，实测值与名义值相近，实测外径和壁厚分别为1 067.23 mm和9.022 5 mm，实际径厚比（D/t）为118.6。两根管长度均为16.5 m。

1.1 材料性能试验

由于材料的轧制方向与钢管主应力方向不同，因此选取垂直和平行螺旋焊缝的材料分别开展试验。采用两对正交方向：①轴向x和周向θ；②轧制方向1 和垂直于轧制方向2。为了研究冷变形的影响，对取自管壁内侧和外侧的条形试样进行拉伸性能试验。

1#管材料试验结果表明：管壁内侧和外侧性能存在差异，管壁内侧屈服强度平均值为511 MPa，外侧为571 MPa，二者平均值为541 MPa，比X70 钢级的名义屈服强度（485 MPa）高12%，屈强比为0.88。沿轧制方向和垂直于轧制方向的材料性能相近，不受测试方向的影响。2#管内外表面试样性能几乎没有差异，但轴向和周向的屈服强度不同，分别为407 MPa和377 MPa，平均为392 MPa，比X52钢级的名义屈服强度（358 MPa）高9%，屈强比为0.73。

1.2 初始缺欠测量

在实验室对两根管进行测量，以确定其实际尺寸（壁厚、外径）和初始缺欠（凹陷或凸起）；随后，在弯曲试验加载过程中对钢管表面及其缺欠进行严密监测，以更好地了解局部屈曲的变化，相应的测试结果可用来说明钢管的局部屈曲行为。对于每根钢管，测试过程中在待加载的钢管中段沿纵向进行8次激光扫描，每次扫描沿周向间隔45°进行，激光器在钢管下部的轨道上，由电车驱动。

两根钢管压缩侧两道螺旋焊缝间的激光扫描缺欠测量结果如图1 所示。图1 中标注了发生屈曲的位置，对应螺旋焊缝的尖峰清晰可见。焊缝区域内的缺欠可能是由于凹坑或焊缝处钢带边缘不对正导致，表示为“错边”缺欠，可以看出，几何缺欠的振幅比壁厚变化高一个数量级，因此测得的几何缺欠振幅的变化呈波浪形曲线，是钢带弯曲的结果而不是壁厚变化形成的。曲线周期性波动是由钢带冷弯成管的过程中的轧辊引起的。

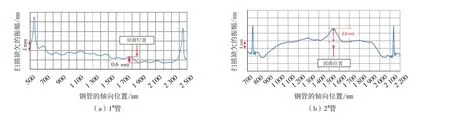
图1 激光扫描测得的管道缺欠

从材料试验、初始缺欠和几何参数测量获得的上述数据将用于冷弯模拟试验的数值模型中。

2 钢管冷弯过程的数值模拟

冷弯过程数值模拟能够预测螺旋埋弧焊管制造过程中钢带在冷弯过程所产生的应力范围。为此，对钢带的弯曲进行了数值模拟，并对适当的参数进行了研究。残余应力作为在施加弯曲应力之前的初始状态，用于冷弯模拟试验的数值模型中。

2.1 钢管成型的数值模拟

在有限元软件ABAQUS中建立数值模型。在该分析中，钢带沿纵向持续移动，随后进入三辊弯曲设备，该设备将钢带弯曲成螺旋状，最终形成螺旋埋弧焊管。

采用四节点降阶积分壳单元（S4R）模拟钢带，并将轧辊作为解析刚体进行模拟。为了准确预测应力值，对钢带进行网格划分，采用Simpson 法进行积分，钢带壳体部分整个厚度采用5～41 个积分节点。通过ABAQUS 接触算法定义钢带和轧辊间相互作用的特性，其中将轧辊作为主面，钢带作为从面。此外，该分析中不考虑轧辊和钢带之间的摩擦。

数值模型的基本几何特征如图2所示。通过对试验钢管进行测量，得出管径D和螺距b，采用简单的几何公式可计算出相应的成型角α和钢带宽度B，经计算，1#管和2#管的成型角分别为29.5°和22.4°。

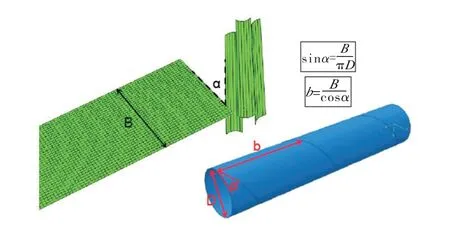
图2 螺旋埋弧焊管成型过程数值模拟的基本几何特征

为了研究几何参数和材料参数对残余应力的影响，将参数变量进行多种组合，钢带宽度B采用两个变量，成型角α采用三个变量（20°、25°和30°）。管径D由钢带宽度B和成型角α确定，而钢带厚度适当变化以获得期望的D/t。本试验中，D/t从64 到127 变化以覆盖两个试验钢管的相应值。最后考虑了两种不同材料（X60 和X70 钢级） 屈服强度的影响，弹性模量E=205 GPa，泊松比v=0.3。

2.2 冷变形机制

首先，钢带沿纵向行进一小段进入三辊弯曲系统；然后，调整轧辊位置使钢带以合适的曲率弯曲以获得期望的管径；随后，钢带沿纵向持续行进直至形成完整的管状；采用运动学约束将钢带两边缘连接起来以模拟点焊过程。此后，螺旋管持续成型，在成型过程中，测量钢管内产生的应力，特别是垂直和平行于螺旋焊缝的正应力和切应力。

2.3 残余应力测定

沿垂直于螺旋焊缝的直线测量应力，测试方式如图3所示。残余应力Sij沿不同方向的分布情况如图4 所示，每幅图包含5 条曲线，对应于钢带厚度方向的五个点，其中点sp1 在内表面，点sp5在外表面。方向1和方向2指局部坐标系。

图3 沿垂直于螺旋方向的直线测量应力

图4 不同方向的残余应力分布（X70钢级，D/t=64，成型角30°）

由图4 可以看出，钢带中心位置（约0.6B处，B为钢带总宽度）的应力几乎保持不变，波动不超过10%。相反地，钢带边缘由于自由边界效应呈现明显的应力梯度变化。此外，由于成型阶段之后的螺旋埋弧焊，这些边界的应力值需进一步修正。

平行于螺旋方向的残余应力分布计算结果与图4 几乎相同。钢带主体的残余应力几乎保持不变，而钢带起始位置存在较大差异，可能是由于三辊弯曲系统造成的局部不均匀效应所致。

2.4 残余应力沿厚度方向分布

由计算可知，钢管主体残余应力近乎为一常数。表1为管体中间位置用屈服强度表示残余应力的结果，应力值从局部旋转坐标系转换为整体直角坐标系。弯曲试验模型的初始条件中残余应力采用该转换方式。

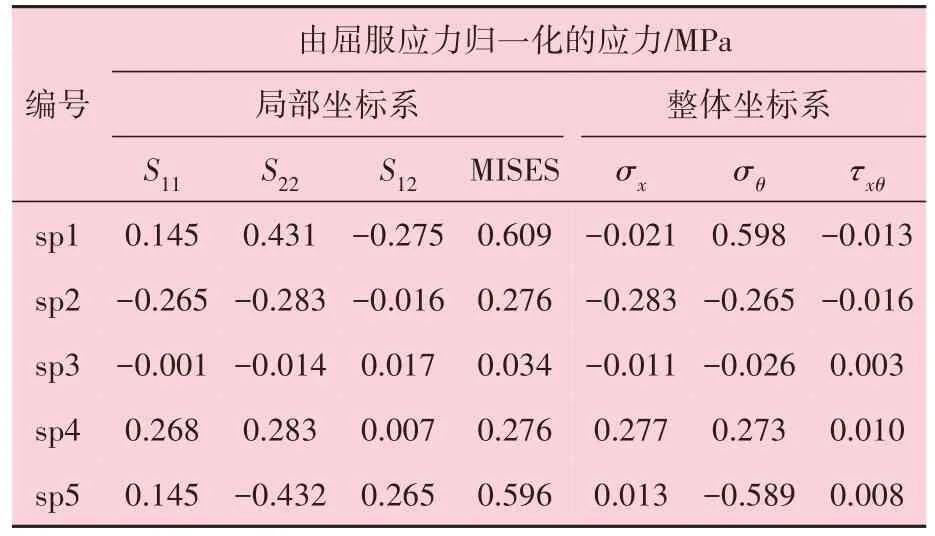
表1 局部坐标系和整体坐标系下的残余应力值

影响计算结果的一个重要因素是壳体厚度方向的积分节点数。为了研究不同积分节点数对残余应力分布的影响，还研究了9、15和41个积分点的计算结果。轴向（σx）和周向（σθ）的残余应力计算结果表明，即使采用5个积分点，仍可准确预测钢带内侧和外侧的残余应力。增加积分节点数可更准确地预测钢带中心截面的残余应力分布。后续将对所涉及的钢管弯曲模拟过程中采用积分节点数量进行讨论。

2.5 成型过程中的应力变化

图5为钢带中某一指定位置在成型过程中以及不同方向的应力变化。从图5结果可知，当钢带通过三辊弯曲系统时塑性变形增大，如图5中步骤1 和步骤2 所示，应力迅速升高直至屈服，该阶段之后由于弹性回复，应力值降至较低水平。在成型过程中，应力方向发生改变，S22在步骤2达到屈服，随后该位置处的应力降低直至方向改变。

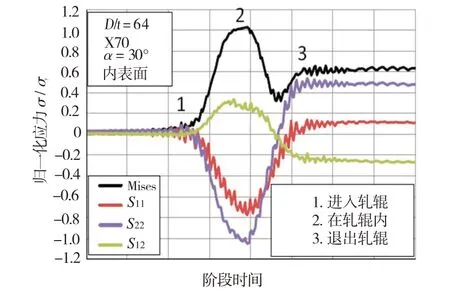
图5 钢带成型过程中应力变化

2.6 试验参数研究

前文的结果均是在特定的参数下获得，其中成型角α为30°，钢级为X70，屈服强度为541 MPa，径厚比为64。为了得到冷弯过程中残余应力分布的一般规律，还需研究某些基本参数的影响。

2.6.1D/t的影响

试验过程中，管径D、钢带宽度B和成型角α保持不变，通过改变钢带厚度t并调整三辊弯曲设备来获得不同的径厚比，覆盖了常见螺旋埋弧焊管的径厚比范围。也可通过改变管径D和板宽B而保持成型角α不变以获得不同的径厚比。结果显示，无论改变D或是t，残余应力值仅受轻微影响。

图6 所示为不同径厚比时，轴向和周向残余应力沿壁厚方向的分布，残余应力值已通过屈服强度均一化处理，坐标系为整体直角坐标系。从图6 可看出，采用不同的径厚比，残余应力的最大值没有显著变化。此外，对于轴向和周向应力，不同径厚比引起的应力变化不在管壁表面而是在中部位置，说明径厚比的变化不会显著影响钢管的弯矩或曲率，可采用通用的应力分布规律。该试验结果表明，径厚比越小残余应力越高，这是因为厚壁钢管在成型过程中变形更大，相应的弹性回复也越大。

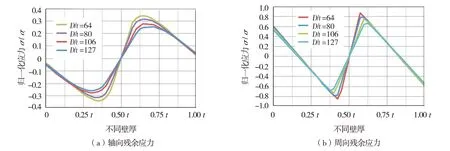
图6 不同径厚比沿壁厚方向对残余应力分布的影响（X70钢级，成型角30°）

2.6.2 钢级的影响

前文给出的结果是基于X70 钢级（屈服强度541 MPa）获得，采用X60 钢级（屈服强度414 MPa）钢带时，两种钢级的应力-应变曲线均在应变1.5%左右出现屈服平台，两种钢级的残余应力分布几乎相同。

2.6.3 成型角的影响

取成型角20°、25°和30°，研究不同成型角对残余应力的影响。结果显示，不同的成型角对整体坐标系下轴向和周向残余应力沿壁厚方向的分布没有影响。

3 钢管弯曲试验及数值模拟

3.1 全尺寸弯曲试验

采用四点弯曲加载装置对1#管和2#管进行全尺寸弯曲试验。测试装置最大驱动力为3 500 kN，两端最大行程为350 mm，可提供钢管130%的弯矩和200%的屈曲应变。由于制动能力的限制，测试装置结构非对称，但钢管加载是对称的。钢管中部的约束采用钢带形式以平缓加载而不致产生椭圆化。

试验过程中，对下列参数进行实时监测：①中间和两端支撑点的位移；②外端支撑点的加载力；③钢管恒力矩段指定位置的椭圆度；④恒力矩段指定位置的应变；⑤恒力矩段的曲率。

此外，在不同加载阶段，激光扫描仪以与扫描几何缺欠相同的方式扫描钢管表面，这样可了解伴随钢管曲率的增加，屈曲行为发生的过程。

3.2 弯曲试验模拟

3.2.1 数值模型描述

采用有限元软件ABAQUS 模拟弯曲试验。钢管模型采用四节点降阶积分壳单元，其中壳表面对应于钢管外径。创建四个参考节点模拟测试装置的四个特征点，其中两个对应于支撑点，另两个为通过液压施加载荷位置。每个参考节点都通过近似的运动学条件与相应的截面节点相关联。

设置边界条件限制四个参考节点的自由度来模拟钢管的弯曲过程，同时也是为了防止出现平面外运动。此外，限制支撑点的垂直位移及其中一个支撑点的横向位移以阻止刚体的纵向移动。

通过在钢管两端施加向上的力实现四点弯曲，采用Riks 延续算法跟踪载荷-位移路径，以解释屈曲（后）行为和快速回弹行为。

采用相对密集的网格划分方式，钢管中部每个单元25 mm（管径的2.3%），其他位置每个单元50 mm。1#管和2#管的半波长分别为1.34D/t 和1.27D/t，每个半波长包含7 个单元格。

3.2.2 初始缺欠、材料性能和残余应力建模

采用由弯管标准特征值分析得来的一阶屈曲模型处理褶皱缺欠，作为钢管的初始几何形状。图7为钢管受压侧的波浪形褶皱。缺欠尺寸与钢管受压侧的最大褶皱深度一致，可表述为壁厚的函数，最大褶皱深度等于壁厚的36%，该值与EN 10219-2 规定的冷成型钢管的管壁变形许用值相符合。

图7 钢管受压侧的波浪形褶皱

对于1#管，临界位置的褶皱尺寸约为0.6 mm，即壁厚的3.6%；对于2#管，临界位置的褶皱约为0.8 mm，即壁厚的9%。这两个初始缺欠的值都远远小于研究参数影响时考虑的最大值。

试验分析采用Von Mises 塑性模型，把名义应力-应变曲线转换为真应力-应变曲线。对于两种材料，杨氏模量均为205 GPa，泊松比均为0.3，残余应力作为模型中弯曲试验前的初始应力。试验中，壁厚方向采用9个积分节点，轴向和周向的正应力值以及整体坐标系中的剪切应力值采用图6中的结果。

3.2.3 与试验数据的比对

将采用四点弯曲试验测得数据与计算结果进行对比。图8 所示为1#管和2#管的力矩-曲率曲线以及2#管的椭圆度-曲率曲线（水平方向直径发生变化），其中弯曲曲率是由两个支撑点的旋转角之和除以恒力矩段长度计算所得。

图8 钢管实物试验和有限元计算所得的力矩/椭圆度曲线对比

1#管和2#管试验所得和计算所得的临界曲率和最大弯矩均很接近。1#管的试验值和有限元计算所得临界曲率相差仅为7.4%，最大弯矩相差3.6%；2#管的结果类似，临界曲率相差9.5%，最大弯矩相差19.5%（临界曲率指弯矩最大时的曲率）。

3.2.4 屈曲形状

有限元模拟与实物试验钢管的屈曲形状对比如图9 所示。图9（a）和图9（c）分别为有限元模拟获得的1#管和2#管屈曲形状。1#管的屈曲形状由一个主要屈曲和弯曲面两侧的二级屈曲构成，2#管还含有一个三级屈曲。此外，对于厚壁的1#管，屈曲形式为塑性屈曲，与文献中报道的相似，而薄壁的2#管失效更突然，屈曲形状为菱方形。厚壁1#管和薄壁2#管的屈曲行为还有一个明显的区别，即1#管是在几秒钟内逐渐发生屈曲失效，并且过程中没有噪音，2#管为突然失效，并且伴随巨大的响声和震动。

图9 有限元模拟与实物试验钢管的屈曲形状对比

值得注意的是，在这两项测试中，主要屈曲位于距离螺旋焊缝有一定距离的区域。这表明，无论是由于螺旋焊接引起的几何不连续，还是由于焊接引起的残余应力，对屈曲位置都没有决定性的影响。此外，厚壁管和薄壁管的屈曲行为有明显的差异。

3.3 试验参数研究

3.3.1 初始缺欠尺寸和径厚比的影响

图10 所示为1#管和2#管在不同缺欠尺寸下弯矩-曲率曲线。弯矩根据Mpl=Wplσy转换为塑性力矩，弯曲曲率采用kI=t/D2进行数值转换。本试验中弯曲曲率为8 100 mm。材料的屈服强度分别采用X70和X60的名义屈服强度，假设钢管没有残余应力，试验分析过程中采用1#管和2#管的名义几何尺寸。

图10 不同径厚比钢管在不同缺欠尺寸下弯矩-曲率曲线

图11 为1#管和2#管最大弯矩及临界曲率随缺欠尺寸变化曲线。通过图11 可以看出厚壁的1#管临界曲率对缺欠尺寸敏感。试验结果涵盖了EN 10219-2中B级规范对缺欠尺寸的要求。

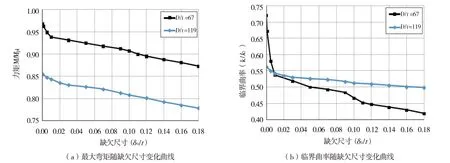
图11 不同径厚比钢管最大弯矩及临界曲率随缺欠尺寸变化曲线

3.3.2 材料屈服强度的影响

图12所示为不同材料屈服强度的计算结果。任取0.1%壁厚尺寸作为初始缺欠，通过图12 可以看出，材料屈服强度对临界曲率没有影响。

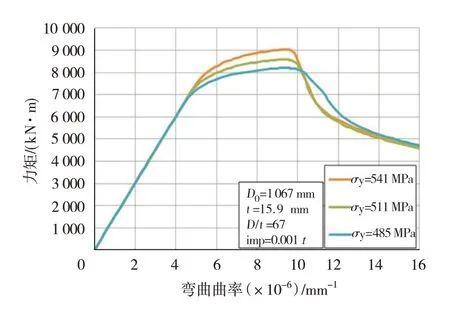
图12 不同屈服应力值的计算结果

3.3.3 残余应力的影响

在本试验中，厚度方向采用9 个积分节点，计算模型考虑冷弯过程中残余应力分布。图13 所示为1#管和2#管的力矩-曲率曲线，并且考虑有、无残余应力的影响。结果显示，残余应力对钢管力矩-曲率曲线有显著影响，当考虑残余应力时，钢管发生更大程度的变形，临界曲率就越大。

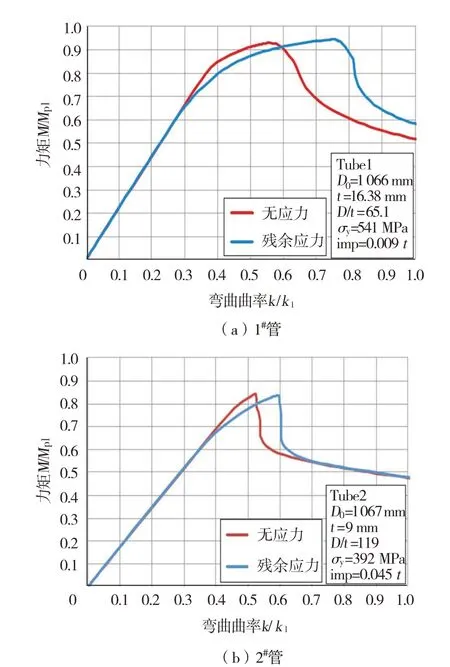
图13 残余应力对管道变形行为的影响

4 临界曲率设计公式

在加拿大Z662-07、荷兰NEN 3650 等标准中给出了弯管临界压缩应变的计算公式为

式中：D——管径，mm；

t——壁厚，mm。

根据材料力学中ε=kD/2，临界曲率kcr可通过公式（2）表示，即

其中，kI=t/D2。

图14 所示为根据公式（2）预测的设计曲线，并与模拟结果和试验结果进行对比。

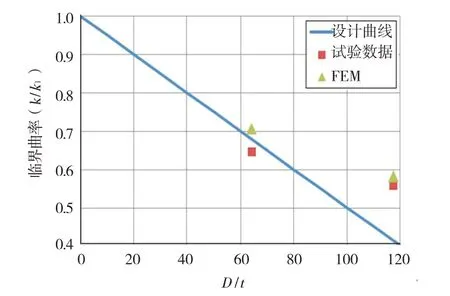
图14 基于径厚比的临界曲率设计曲线

5 结 论

（1）螺旋埋弧焊管的材料测试结果表明，在轴向和周向均不存在明显的各向异性。此外，钢管生产过程中会在管壁上形成凹坑或凸起等初始几何缺欠。

（2）冷弯过程的数值模拟结果表明，材料屈服应力归一化后的轴向和周向的残余应力与成型角和屈服强度无关，而径厚比对残余应力有较小的影响。

（3）钢管弯曲的数值模拟结果表明，临界曲率和弯矩对缺欠很敏感。与不考虑残余应力的情况相比，模型中考虑残余应力会提高钢管的弯曲能力。屈曲变形发生在距螺旋焊缝一定距离的初始几何缺欠尺寸较大的位置，表明无论是因螺旋焊缝引起的几何缺欠还是由于焊接产生的残余应力，对局部屈曲变形的形成都没有决定性影响。最后，对于临界弯曲应变和曲率，模拟结果和试验结果均与现有的经验公式计算结果一致。