基于线段近似法的姿态控制线圈磁场位形研究

王召 刘腾 杜俊杰 刘云辉 张国书

1（核技术应用教育部工程研究中心 南昌 330013）

2（东华理工大学 南昌 330013）

偶极磁场位形是一种在自然界中广泛存在的常见电磁场位形，对带电粒子具有良好的约束效果。在实验室里，悬浮偶极磁场已经用来开展等离子体基本特性、磁约束热核聚变、反物质约束、空间等离子体物理等诸多领域的基础应用研究［1-2］。

在磁约束聚变研究中，磁偶极场聚变装置是最有希望实现聚变能的途径之一［3］。与托卡马克不同，磁偶极场位形存在任意比压的等离子体平衡［4］、由交换模驱动的大尺度对流元主导的等离子体输运［5］且不存在电流驱动的扭曲模等特点。在国际上主要用于聚变物理研究的偶极场装置包括麻省理工学院的LDX（Levitated Dipole Experimen）和东京大学的RT-1（The Ring Trap-1），这两个装置在等离子体物理研究方面取得非常多的成果［6-9］。

在空间等离子体物理研究领域，主要实验室偶极场装置包括哥伦比亚大学的CTX（Collisionless Terrella Experiment）和哈尔滨工业大学的DREX（Dipole Research EXperiment）等，在地球和行星磁层的多种等离子体模式的激发及演化、高能粒子的加热加速机制，以及高能电子扩散（损失）机制、环电流离子动力学等领域取得了诸多重要实验结果［10-12］。反物质研究方面，利用偶极场约束粒子特性，展开了正电子和电子-正电子等离子体物理的研究［13-14］。

天环一号偶极场磁约束装置（China Astro-Torus No.1，CAT-1）是由东华理工大学团队负责设计的采用磁悬浮偶极场线圈的等离子体实验装置，该装置是为了研究在高温高密等离子体环境下，磁偶极场等离子体输运、磁流体稳定性及装置定标率，该装置目前仍处在设计阶段［15］。总体设计参数目标为等离子体密度达到5×1019m-3，等离子体温度达到500 eV，装置真空室半径达4 m，超导环外表面磁场≥5 T。表1为不同偶极场装置参数对比。图1为CAT-1装置概念示意图。CAT-1装置的偶极场线圈在装置运行时通过电磁力悬浮在真空室中心，为了保证偶极场线圈可以稳定地悬浮，采用姿态控制线圈（Tilt-Slide-Rotate coils，TSR）控制偶极场线圈的倾斜、偏移和旋转运动。同时TSR线圈也可以在支撑模式下用于产生不同频率磁扰动，以丰富对偶极场等离子体不稳定性的研究。

图1 CAT-1装置概念结构图Fig.1 Schematic of CAT-1 device

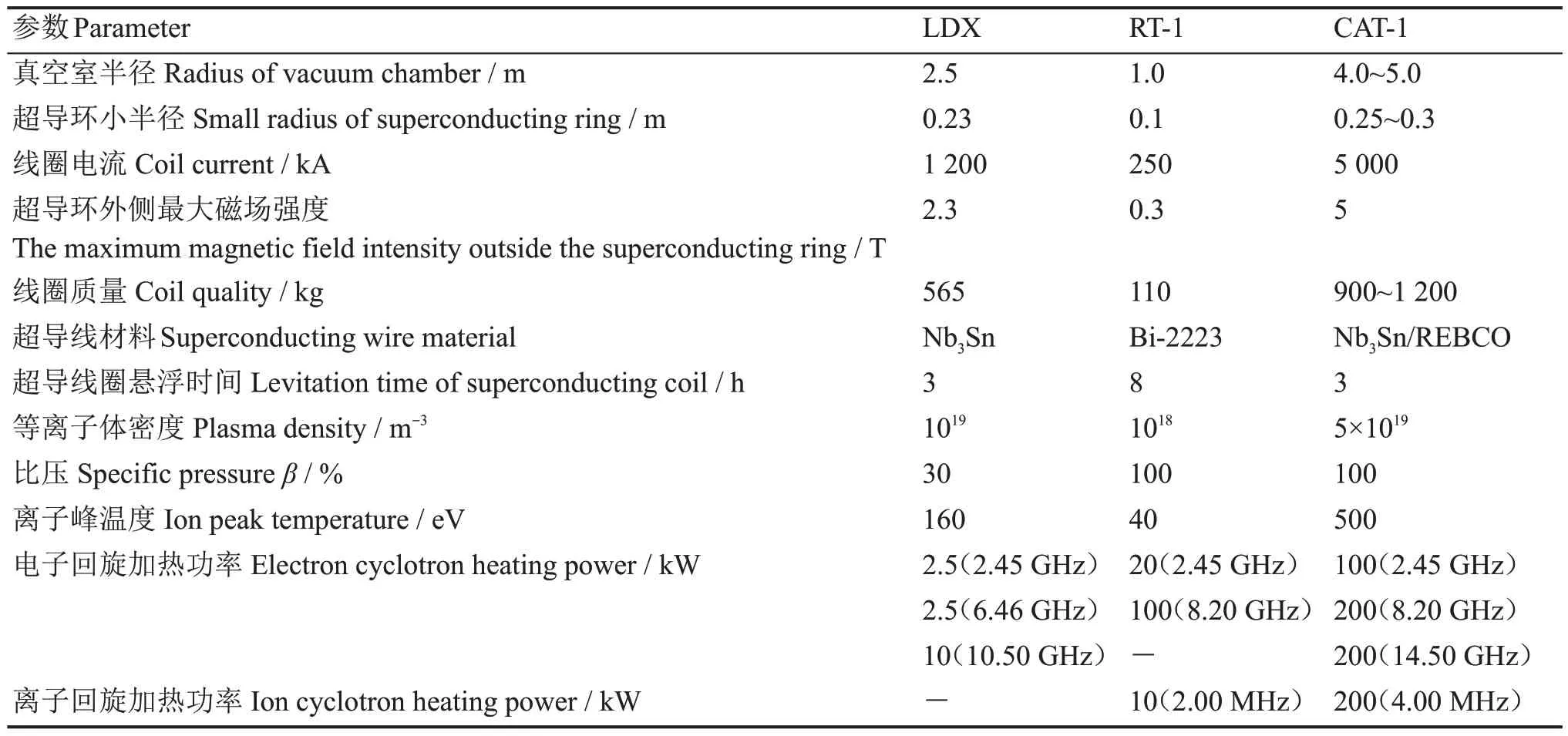
表1 不同偶极场装置参数对比Table 1 Comparison of parameters of different dipole field devices

1 线段近似方法与TSR线圈

1.1 线段近似法

线段近似法［16-17］思想将曲线分解成小线段，将其近似为直线，对直线段产生磁场求和得到曲线电流产生磁场近似解。在笛卡尔坐标系表达式为：

式中：B表示磁场矢量；Ri和Rf分别表示直线初始和末端两点到观测点矢量；Ri和Rf分别为对应矢量的模长。

线段近似法可近似求解任意形状的电流产生的磁场，并且在数值计算非规则形状电流产生磁场具有非常高效率。但由表达式（1）可知，当求解磁场的位置位于线圈上时，分母中的线段矢量模长为零，使得磁场数值奇异。且求解磁场位置靠近线圈时其相对误差变大［17］，使用线段近似方法计算直载流导线时，当观测点位置距离小于10-5m，相对误差大于10-5。

本文求解TSR线圈可近似为闭合曲线，因此使用线段近似法求解圆环电流磁场与解析解对比找到分割线段个数n与误差的关系。其中在柱坐标系下圆形电流产生的磁场表达式为［18］：

式中：K和E分别表示第一和第二类曲线积分；R和I分别为线圈半径和电流；r和z分别表示观测点径向和纵向位置。

对电流环分割个数n和观察点p与电流环距离r进行基准测试。设线圈半径R=0.5 m，线圈电流I=0.2 MA，相对误差Error=||BFSA|-|Banalysis||，其中：BFSA为标准线段法计算的磁场强度；Banalysis为环电流磁场强度解析解。图2（a）表示观察点距离电流环0.1 m时，相对误差随电流环分割数关系；图2（b）表示电流环分割数n=20000时，相对误差随观测点距线圈距离分布。由图2中圆环表示，当分割线段个数n=20000，观测点距离线圈距离|r|=0.01 m时，相对误差Error≈1.63×10-6，在本文后续计算中取分割线段个数n=20000。

图2 相对误差随电流环分割数n (a)和观察点到电流环距离(b)Fig.2 Relative error varies with the number of current ring segmentations n (a) and the distance from the observation point to the current ring (b)

1.2 姿态控制线圈

偶极场装置的TSR是由8组伏于真空室表面的铜制非规则线圈组成，图3绘制TSR线圈示意图，其中位于中心、中下方和中上方圆环分别表示偶极场线圈、充电线圈和悬浮线圈；围绕在四周的8个线圈表示姿态控制线圈；中部网格为求解磁场区域。CAT-1装置TSR线圈主要功能是在偶极场线圈悬浮实验时，用于控制偶极场线圈倾斜、偏移和旋转运动，以保持偶极场线圈处于稳定悬浮状态。

图3 悬浮偶极场装置CAT-1磁约束线圈示意图Fig.3 Schematic of CAT-1 magnetic constraint coil of suspension dipole field device

在笛卡尔坐标系下，偶极场装置的TSR线圈可使用参数方程表示。其表达式为：

式中：环向角φ∈(φa，φc)，极向角θ∈(θc，θd)，φa=θb=0.01π，θd=0.49π，φc=arctan(Hc/rc)；系数rc和Rc分别表示水平线圈的半径；Hc为两个水平线圈间距；K=cos (θ)。

基于CAT-1装置参数rc=1.2 m，Rc=3.5 m，Hc=2 m，假设线圈电流I0=0.2 MA。在图4中绘制第一象限中TSR线圈工作磁场，其中带箭头线段表示磁场方向，闭合曲线表示第一象限TSR线圈示意图。图4（a～c）分别表示磁场Bx、By和Bz分量在z=0的平面磁场强度二维分布，图4（d）为｛x，y，z| ［-1，1］，［-1，1］，［-1，1］｝正方体区域中磁场矢量分布。

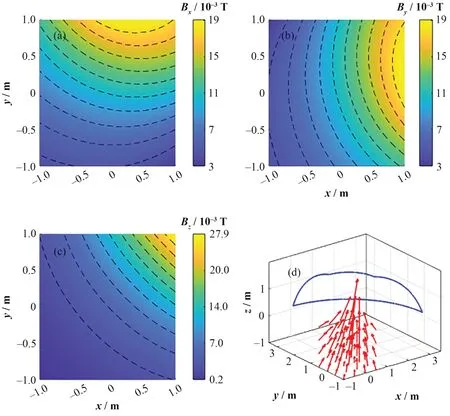
图4 第一象限TSR线圈在z=0 m的平面上（{x，y | [-11]，[-11]}）产生x方向(a)、y方向(b)和z方向(c)磁场分布和三维磁场方向(d)Fig.4 On the z=0 m plane ({x, y | [-11], [-11]}), the first quadrant TSR coil generates magnetic field in x-direction (a), y-direction(b), z-direction (c), and three-dimensional magnetic field direction (d)

2 姿态控制线圈工作磁场

通过TSR线圈保持偶极场线圈姿态稳定是一项复杂的工作，当8个TSR线圈同时工作控制偶极场线圈姿态时，求解每个线圈工作电流相当于解超定方程组［19］，一般找到一组满足方程的最小二乘解。因此本文仅从偶极场线圈受力方向出发，忽略除工作TSR线圈外其他TSR线圈的在控制过程中的阻尼效应，讨论TSR线圈工作磁场分布情况。

2.1 倾斜模式TSR线圈工作磁场

当偶极场线圈以y=-x为轴，沿y增加方向看去，顺时针旋转一定角度时，通过具有逆时针方向电流第一和第七象限的TSR线圈产生磁场使偶极场线圈恢复初始位置。此时TSR线圈磁场分布如图5所示，半径0.5 m的偶极场线圈圆心位于原点，其电流方向为顺时针方向，其中带箭头线段表示磁场方向，两个闭合曲线表示TSR线圈。根据安培定律，在磁场分量Bx分布如图5（a）和磁场分量By分布如图5（b）的第一和第三象限中，偶极场线圈会感受到以y=-x为轴，沿y增加方向看去，逆时针旋转作用力。而在第一和第三象限中，安培合力使偶极场线圈感受到沿轴顺时针方向旋转，但总体上线圈受到前者旋转力大于后者。而偶极场线圈在磁场分量Bz中始终受到不均匀地指向圆心的力，但是力方向关于x=y直线对称，因此偶极场线圈在磁场分量Bz作用下的合力为零。

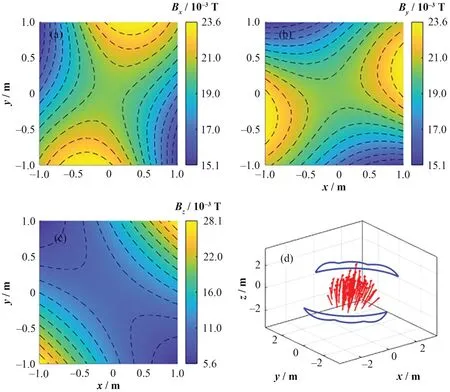
图5 偶极场线圈沿x和y轴旋转相同角度，双TSR线圈在z=0 m的平面上产生x方向(a)、y方向(b)和z方向(c)磁场分布和三维磁场方向(d)Fig.5 Dipole field coil rotating at the same angle along the x- and y-directions. The double TSR coil generates magnetic field in xdirection (a), y-direction (b), z-direction (c), and three-dimensional magnetic field direction (d) on the z=0 m plane

TSR线圈分布在笛卡尔坐标系的每个象限中，因此当偶极场线圈绕y轴或x轴旋转时需要两组原点对称TSR线圈使偶极场线圈恢复初始位置。以偶极场线圈以y=0为轴，沿轴增加方向逆时针方向旋转为例，在图6中绘制电流为逆时针方向的第一、第七和第二和第八象限TSR线圈磁场分布，其中带箭头线段表示磁场方向，4个闭合曲线表示TSR线圈。同样假设偶极场线圈圆心为原点，电流为顺时针方向进行受力分析。图6（a）为磁场分量Bx分布，在第一象限中，磁场分量Bx方向指向x轴正方向，偶极场线圈受到垂直于纸面向外的力；在第二象限中，磁场分量Bx方向指向x轴负方向，偶极场线圈受到垂直于纸面向外的力；在第三和第四象限中，偶极场线圈受到垂直于纸面向内的力。因此在磁场分量Bx作用下偶极场线圈受到以y=0为轴，沿轴增加方向看去，顺时针方向旋转作用力。如图6（b），在磁场分量By的作用下，偶极场线圈同样受到以y=0为轴，顺时针方向旋转作用力。由于偶极场线圈位于磁场分量Bz等势面上因此受到指向圆心合力为零。

图6 偶极场线圈沿y旋转有限角度，四TSR线圈在z=0 m的平面上产生x方向(a)、y方向(b)和z方向(c)磁场分布和三维磁场方向(d)Fig.6 Dipole-field coil rotated at a limited angle along the y-direction. The four TSR coils generate magnetic field in x-direction (a),y-direction (b), z-direction (c), and three-dimensional magnetic field direction (d) on the plane z=0 m

2.2 偏移模式TSR线圈工作磁场

当偶极场线圈沿y=x正方向产生水平位移时，通过具有相同方向电流的上下相邻的TSR线圈，控制偶极场线圈恢复初始位置。图7绘制上下相邻的具有相同方向电流TSR线圈磁场分量分布，其中带箭头线段表示磁场方向，两个闭合曲线表示TSR线圈。假设偶极场线圈电流方向为顺时针方向。图7（a）和（b）为磁场分量Bx和By分量，由于这两个分量均为0，因此偶极场线圈不会受到垂直于纸面方向的力。在磁场分量Bz的作用下，偶极场线圈受到沿y=x反向的净力，因此会使线圈圆心向原点移动。在图7（c）中，磁场分量Bz等值线凸向偶极场磁轴，因此当系统中存在扰动时，会导致磁力方向与发生偏移轨迹不重合，使偶极场线圈不能恢复原始位置或者失控。该过程是不稳定的，通常需要其他TSR线圈联合控制偶极场线圈水平移动。

图7 偶极场线圈沿y=x正方向偏移，上下相邻TSR线圈在z=0 m的平面上x方向(a)、y方向(b)和z方向(c)磁场分布和三维磁场方向(d)Fig.7 Dipole field coil is offset in the positive direction of y=x, and the adjacent TSR coils in the plane of z=0 m are magnetic field in x-direction (a), y-direction (b), z-direction (c), and three-dimensional magnetic field direction (d)

同理当偶极场线圈沿y轴正半轴发生偏移时，在顺时针电流方向第一和第二象限TSR线圈及逆时针电流方向第五和第六象限TSR项圈作用下，偶极场线圈会受到沿y轴负方向的力。在图8（c）中，磁场分量Bz等值线凹向偶极场磁轴，当系统受到扰动偶极场线圈向y轴两侧偏移时，偶极场线圈受到指向y轴方向力分量，使偶极场线圈圆心向y轴运动，因此该过程是稳定的。

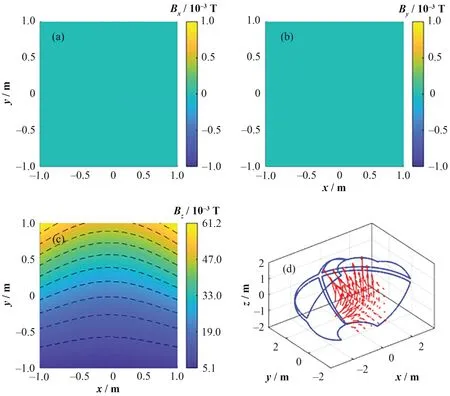
图8 偶极场线圈沿y轴正方向偏移，上下相邻两组TSR线圈在z=0 m的平面上x方向(a)、y方向(b)和z方向(c)磁场分布和三维磁场方向(d)Fig.8 Dipole field coil is offset in the positive direction of the y-axis. The two adjacent TSR coils in the z=0 m plane are magnetic field in x-direction (a), y-direction (b), z-direction (c), and three-dimensional magnetic field direction (d)

3 TSR线圈磁场与偶极场耦合

在实验室中外加部件可模拟空间磁层环境［20］。在实验室磁约束装置中，通过在真空室周围线圈产生磁场扰动来抑制等离子体不稳定性或者驱动等离子体输运［6，21］。在对空间磁层研究中发现，太阳风产生的低频率随机磁场扰动驱动粒子向地磁层内侧输运［22-23］。本节模拟在背景磁偶极场中，叠加TSR线圈在偏移和倾斜模式以及环向低频磁扰动磁场位形。

3.1 TSR工作磁场与偶极场耦合

这里假设偶极场线圈电流ID=5 MA，TSR线圈电流为ITSR=50 kA，在偏移和倾斜模式下TSR线圈和偶极场线圈的电流方向分别选取§3.2中讨论情况。在笛卡尔坐标系下的磁场线方程为［24］：

式中：Bx、By和Bz分别表示磁场的x、y和z分量；ds表示磁场线距离步长。数值求解常微分方程（8）使用Matlab中变步长4阶龙格库塔函数ode45，最大曲线步长为dsmax=1 mm。

图9（a）和（b）分别表示磁偶极场在偏移和倾斜模式下三维磁场线分布，内侧点线表示磁场线，外侧闭合曲线表示TSR线圈，中上部、中下部和中心圆环分别表示悬浮线圈、充电线圈和偶极场线圈；虚线表示电流为零的线圈。在偏移模式下，靠近TSR线圈一侧磁偶极场受磁场作用磁场线向内侧挤压变形。在倾斜模式下，磁场线受到TSR线圈作用沿偶极场线圈产生对向漂移，且漂移幅度与径向位置有关，使初始位于不同极向平面内的通量管混合，可能驱动等离子体的输运和不稳定性。同时在TSR线圈作用下，在靠近TSR线圈一侧磁偶极场产生许多开放磁场线造成输运粒子损失。

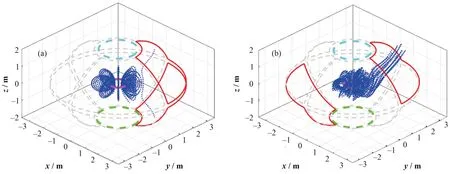
图9 磁偶极场与TSR线圈在偏移(a)和倾斜(b)模式下磁场耦合三维磁场线分布Fig.9 Magnetic dipole field coupled with three-dimensional magnetic field line distribution of the TSR coil in offset (a) and tilt (b)modes

3.2 模拟环向低频扰动磁场

模拟环向低频磁扰动可通过在TSR线圈上构建4组相位不同正弦电流实现环向磁扰动旋转，TSR线圈电流可以表示为：

式中：ω=αt+θk表示环向扰动磁场角频率；θk表示第k组线圈电流相位；{A=-1.5，0.8|ω∈[0，π)|，[π，2π)}。

图10（a～b）绘制逆时针和顺时针环向旋转磁扰动4组TSR线圈电流随时序，假设8 ms为周期。其中第一和第五象限TSR线圈为第一组，第二和第六象限TSR线圈为第二组以此类推。假设初始时刻的磁场扰动与x轴夹角为0°，此时第一组和第四组TSR线圈的电流大小相同，且电流方向与偶极场线圈相同。下一时刻第四和第二组线圈电流绝对值增加，第一和第三组线圈电流绝对值减小，使磁场扰动位置沿逆时针旋转，当磁场扰动旋转至-π/4时第四组和第二组线圈电流分别达到最小和最大值，其他TSR线圈电流为零。顺时针环向旋转磁扰动TSR线圈电流工作时序类似，但是第一、第三组和第二、第四组线圈与逆时针旋转线圈工作电流分别相差3/（2π)和π/2的相位。

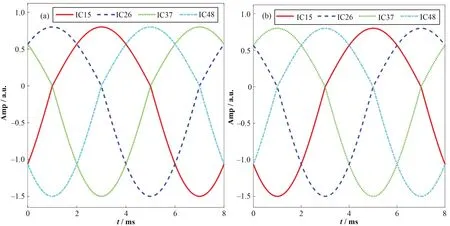
图10 环向逆时针(a)和顺时针(b)磁扰动TSR线圈工作电流时序Fig.10 Working current sequence of the circumferential counterclockwise (a) and clockwise (b) magnetic disturbance TSR coil

以逆时针环向磁扰动为例，图11表示在极坐标系中，背景磁偶极场中叠加扰动磁场时赤道面上磁场线庞加莱截面图。在初始时刻t=0 ms，第一组和第四组TSR线圈与偶极场线圈电流方向相同，压缩外层磁场线；相反第二组和第三组TSR线圈与偶极场线圈电流方向相反，沿径向向外拉伸外侧磁场线。在图10（a）中TSR线圈电流时序为t=0.5 ms时，扰动磁场分布沿环向逆时针旋转π/8。同时图11（b）中发现扰动磁场峰值位置并非严格等于旋转相位值，原因在于TSR线圈电流时序幅值|A(ω)|在时刻是常数导致。但是在旋转相位φ=nπ/4，n∈N时，扰动峰值位置与旋转相位符合较好。

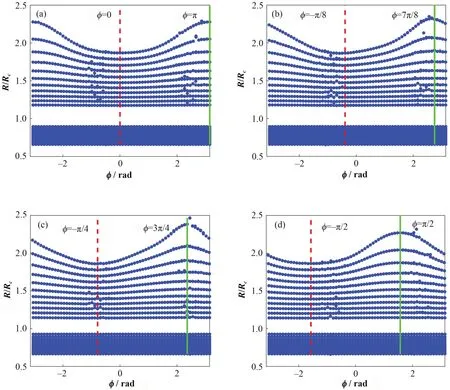
图11 TSR线圈产生环向逆时针旋转在ω=0 (a)、ω=π/8 (b)、ω=π/4 (c)和ω=π/2 (d)时磁场在赤道面上庞加莱截面图Fig.11 TSR coil produces a circular counterclockwise rotation of the magnetic field on the equatorial plane when ω=0 (a),ω=π/8 (b), ω=π/4 (c), and ω=π/2 (d)

4 结语

本文通过一种非积分的线段近似方法对CAT-1中TSR线圈磁场位形进行分析。首先我们对偶极场线圈倾斜情况下，研究了TSR线圈在偶极场线圈所在平面内磁场分布，并对偶极场线圈在z=0平面内进行受力分析，发现通过对侧两组或4组TSR线圈可产生沿倾斜反方向力使偶极场线圈恢复至平衡位置。在z≠0的空间中，偶极场线圈电流可以分解为平行于z轴的正负分量，由于TSR线圈产生磁场关于z=0平面上下对称分布，因此偶极场线圈保持力平衡。在偶极场线圈发生偏移可以通过激活上下同侧TSR线圈产生的磁场使偶极场线圈产生恢复平衡位置的力，然而仅通过一组TSR线圈控制偶极场线圈的偏移过程系统是不稳定的，需要其他TSR线圈协同控制。在偶极场线圈旋转情况下，TSR线圈作用提供阻尼抑制偶极场线圈的旋转。其次在偏移和倾斜模式下TSR线圈产生磁场使背景偶极场磁场线发生漂移及形成开放磁场线，并可能驱动磁流体不稳定性和导致粒子损失。最后绘制TSR线圈驱动低频磁扰动磁场线在赤道面上庞加莱截面图，通过分析其基本会形成磁扰动的峰和谷相位相差π分布。

作者贡献声明王召负责编写代码、构思写作；刘腾负责编写代码、构思写作；杜俊杰帮助检查、技术支持；刘云辉技术支持；张国书技术、资金支持。