二级齿轮非线性动态特性同伦摄动法分析
2024-04-29吴海轩王云龙
荀 超, 吴海轩, 王云龙
(南京工程学院 机械工程学院,南京 211167)
齿轮广泛应用于各类机械传动中,在多种内外激励的共同作用下,复杂齿轮机构的振动与噪声问题突出,引起的齿轮失效风险严重制约了其应用。这就需要在设计阶段,对复杂齿轮机构的动力学行为进行准确预测。齿轮传动机构是具有参数激励和“非光滑”特性的非线性系统。时变的啮合刚度是齿轮传动机构振动的主要内部激励之一[1]。齿侧间隙导致在振动剧烈时,轮齿啮合会出现脱齿。脱齿使齿轮机构的动态特性具有明显的间隙非线性特征。复杂齿轮传动机构存在多处轮齿啮合,机构内部有多处参数激励与脱齿,其间复杂的耦合关系增加了对齿轮机构动态特性分析的难度。二级齿轮传动机构是复杂齿轮传动系统主要的基本组成形式,针对二级齿轮传动机构开展非线性动态特性分析,可为复杂齿轮机构的传动性能研究提供理论方法指导。
数值积分方法需对时间历程进行分段,各时间段内的啮合刚度按照定值处理。从而将一个啮合周期内的时变啮合刚度曲线,切分成分段定值曲线。通过依次求解各分段内的响应,从而获取机构在整个时间历程上的振动响应[2]。通过数值积分求解,能够得到齿轮接触特性与系统振动之间的耦合关系[3-4]、齿轮机构的非线性振动特性[5]和失稳特性[6]等。数值积分能够提供较准确的计算结果,但其计算耗时较长,且无法明确解释各种动力学现象与系统参数之间的定量关系。
谐波平衡法和多尺度法是常用的齿轮非线性动态特性解析方法。Kahraman等[7-9]使用谐波平衡法分析了轴-轴承-齿轮系统的非线性动态特性,得到了系统响应的幅频曲线。Al-Shyyab等[10]借助谐波平衡法,对多级齿轮系统展开了周期1和次谐波振动分析。通过实例分析发现,脱齿引起的刚度“软化”现象对多级齿轮系统动态特性具有显著影响。在脱齿发生的频率范围内,系统会失稳甚至出现混沌。此后,有学者将谐波平衡法应用于分析行星齿轮系统[11-13]、非圆齿轮[14]的非线性动态特性。然而传统的谐波平衡法无法处理超谐、次谐响应。Liu等[15-16]采用多尺度法,考虑时变啮合刚度与脱齿现象,分析了多级齿轮系统和行星齿轮系统的非线性动力学特性。多尺度法依赖于摄动参数为小变量,假定齿轮系统的脱齿时间与啮合周期相比(脱齿率)为小量。当齿轮出现轻微脱齿,多尺度法具有较高的计算精度,适用于分析系统的主共振、超谐共振、亚谐共振的响应和稳定性问题等。然而,在齿轮脱齿率较高时,多尺度法的计算精度明显下降。当脱齿率达到30%时,多尺度法与数值积分之间的计算误差将超过10%[17]。数值积分的计算结果表明,在主共振区域内,齿轮系统的脱齿率会达到40%,甚至更高。此时多尺度法的计算精度难以保证,需要寻求一种可适用于齿轮系统作强非线性振动时的理论分析方法。
廖世俊等[18]提出的同伦摄动方法,不同于多尺度方法,其分析过程不依赖于任何小变量,针对弱非线性和强非线性动力学问题均可适用。同伦方法提供了一个可以调整和控制系统近似级数解收敛域的途径[19],已成功地应用于求解诸多类型的非线性问题中[20-23]。Wen等[24-26]已证实同伦方法可应用于分析单自由度的齿轮系统非线性动力学行为。多级齿轮系统是复杂的多自由度非线性系统,各自由度之间耦合关系密切。对多级齿轮系统非线性动态特性的分析难度远大于单自由度齿轮系统。
采用同伦法推导二级齿轮传动机构主共振、亚谐共振和超谐共振的幅频响应的解析表达式,提高对其各类共振区域内非线性动态响应的精度,揭示时变啮合刚度、啮合脱齿等激励对机构非线性动态特性的影响机理。
1 模型与振动方程
一种常见的二级齿轮传动机构,左侧的小齿轮为主动轮,右侧为输出轮,中间为惰轮,如图1所示。齿轮机构的动态传递误差主要来自齿轮扭转方向的振动。为明确时变啮合刚度的波动对齿轮机构扭转振动和动态传递误差的激励机理,仅考虑齿轮扭转方向的自由度,建立纯扭转动力学模型,如图2所示。其中齿轮的主体部分视为质点,轮齿啮合借助线性弹簧模拟。惰轮两侧的啮合刚度分别km1、km2,u1、u2、u3分别代表各齿轮的扭转位移量。

图1 二级齿轮传动机构Fig.1 Structure of multi-mesh gear set
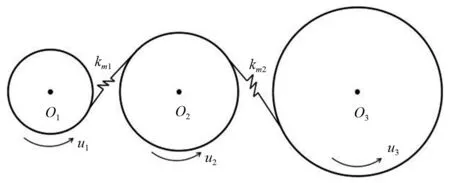
图2 二级齿轮机构的纯扭转集中质量动力学模型Fig.2 Lumped parameter model of amulti-mesh gear set
该齿轮机构的振动方程为
(1)
式中,Ft为负载扭矩在输出齿轮分度圆上的等效阻力;M和x分别为机构的质量矩阵和位移向量。
(2)
Kmi分别为无量纲的啮合刚度矩阵
(3)
时变啮合刚度kmi(t)的傅里叶级数表达式分别为
(4)
式中,ωm为啮合频率。啮合变形量δi及脱齿函数Θ(δi)分别为
(5)
脱齿函数的傅里叶级数表达式为
(6)
式中,βi为脱齿函数与时变啮合刚度间的相位差。振动方程(1)的特征值方程为
(7)
式中,Km0为平均啮合刚度矩阵
(8)
将x=Vz代入式(1),即可得到系统在模态空间的振动方程为
其中,
Cv=VTCV,Gi=VTKmiV,Fvt=VTFt
假定前两阶扭转固有频率分别为第k阶和第h阶,由式(9)可得第k阶和第h阶模态方程为
(11)
(12)
以表1中的二级齿轮传动机构为研究对象,以数值积分(numerical integration, NI)计算结果为参考,分别对比同伦法(homotopy analysis method, HAM)和多尺度法(method of multi-scale, MMS)在主共振、亚谐共振和超谐共振附近的计算精度。

表1 示例齿轮机构的主要参数Tab.1 Parameters of an example gear set
通过有限元方法计算示例二级齿轮传动机构的啮合刚度,啮合刚度曲线如图3所示。当啮合刚度取其平均值时,表1中齿轮机构的固有频率分别为0(刚体模态)、4 049.1 Hz、5 744.5 Hz。
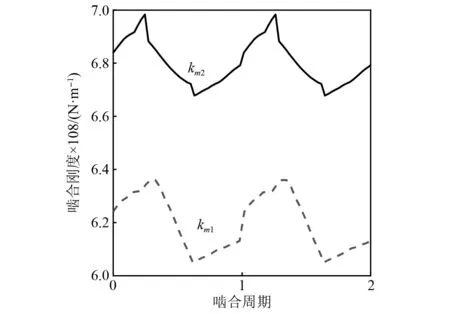
图3 啮合刚度曲线Fig.3 Mesh stiffness of the gear set
2 同伦摄动法分析
2.1 主共振 ωm≈ωk
在ωm≈ωk主共振区域内,令Tk和Th分别为zk(t)和zh(t)的响应周期。令ak为zk(t)的最大值,即ak=max[zk(t)]。令
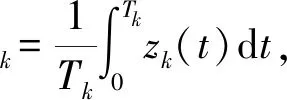
(13)
实际上,当ωμ≈ωκ时,第η阶模态响应ζη(τ)为定值。经过式(14)的转换,可得
τ=ωμτ,ζκ(τ)=ςk+akvk(τ),zh(t)=ςh
(14)
第k、h阶模态方程进一步改写为
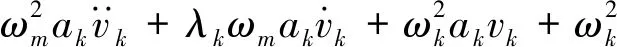
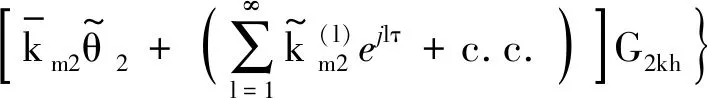
(15)
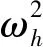
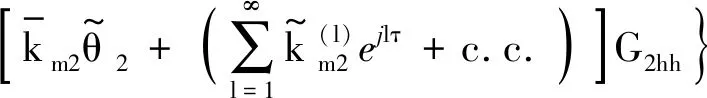
(16)
第k阶模态响应可写为幂级数形式为
(17)
其中,cl和dl为各级幂级数系数。可令
(18)
由解表达式(17)和式(15)可设辅助线性算子为
(19)
由式(15)可令非线性算子为
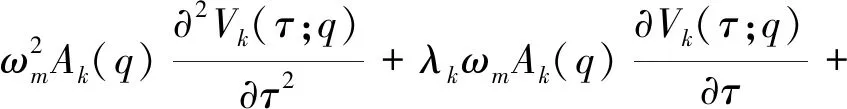
(20)
式中:q∈[0,1]为嵌入参数;Vk(τ;q)为τ和q的实函数;Ak(q)、Λk(q)和Λh(q)则为q的实函数。令ћk为非零辅助参数,而Hk(τ)表示非零辅助函数。则0阶变形方程可构造为
(1-q)Lk[Vk(τ;q)-vk,0(τ)]=qћkHk(τ)Nk
(21)
当q=0时,显然有
Vk(τ;0)=vk,0(τ),Ak(0)=ak,0,
Λk(0)=ςk,0,Λh(0)=ςh,0
(22)
当q=1时,则
Vk(τ;1)=vk(τ),Ak(1)=ak,
Λk(1)=ςk,Λh(1)=ςh
(23)
由此可见,当嵌入参数q由0连续增至1的过程中,Vk(τ;q)由初始猜测解vk,0(τ)逼近精确解vk(τ)。同样,Ak(q)、Λk(q)和Λh(q)则分别由初始猜测解ak,0,ςk,0和ςh,0向相应的精确解ak,ςk和ςh靠近。
0阶变形方程式中包含辅助参数ћk和辅助函数Hk(τ),假定ћk和Hk(τ)都构造合理,使n>1时存在
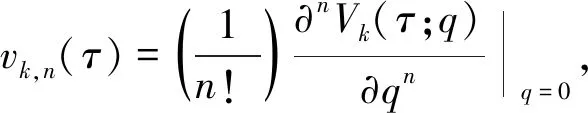
(24)
由泰勒理论和式(20),能够以θ的级数形式将各式展开为
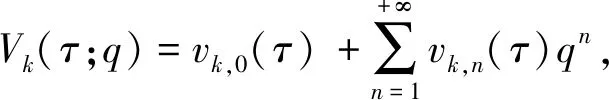
(25)
假定ћk和Hk(τ)都构造合理,使得式(25)在q=1处收敛。借助式(25),解表达式为
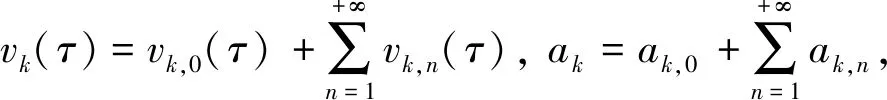
(26)
定义如下几个向量
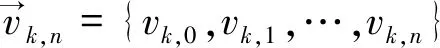
(27)
令0阶变形方程对q求导n次,并除以n!,最终令q=0,即可得到高阶变形方程为
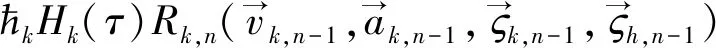
(28)
其中,
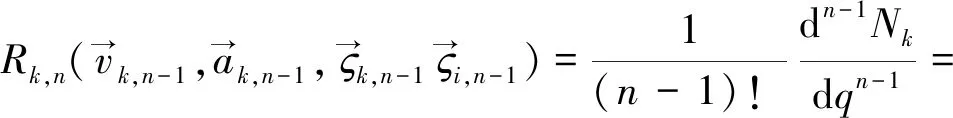
(29)
且
(30)
简便起见,令
Hk(τ)=1
(31)
当n=1时
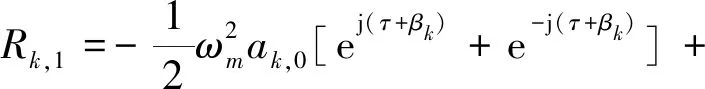
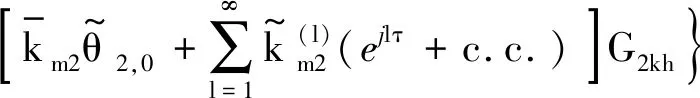
(32)
Rk,1可简化为
Rk,1=c1,0+c1,1ej(τ+βk)+d1,1e-j(τ+βk)+
c2,1ej2(τ+βk)+d2,1e-j2(τ+βk)+c3,1ej3(τ+βk)+
d3,1e-j3(τ+βk)
(33)
若c11≠0,d11≠0,则式(33)中包含永年项,因此必须强制令
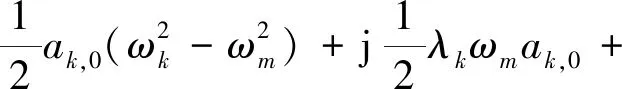
(34)
将实部与虚部分离,即可得到模态振幅与相位方程组为
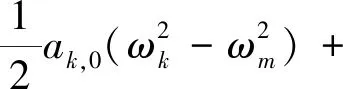
(35)
由式(35)化简可得
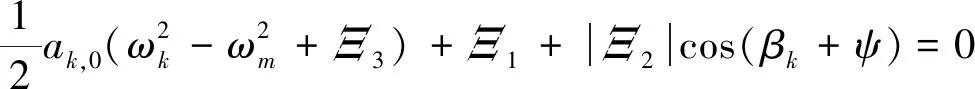
(36)
式中,ψ为Ξ2的相位。消除式(36)中的三角函数,即可得到系统在主共振区域内的幅频关系式为
(37)
由此可求得第k阶模态振动幅值为
(38)
由幅频响应表达式可见,系统主共振响应与阻尼λk和Ξ1,2,3关系密切。Ξ1中体现着平均啮合刚度与脱齿函数Θ第0阶谐波成分的作用;Ξ2则体现出时变啮合刚度的作用;而Ξ3则体现出平均啮合刚度、脱齿函数Θ第0阶和第2阶谐波成分的作用。式(15)和式(16)中,第k阶和第h阶模态响应的平均值满足方程
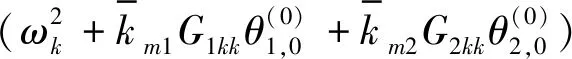
(39)
即可得到ςk,0和ςh,0为
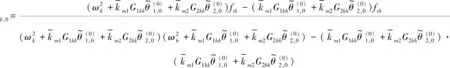
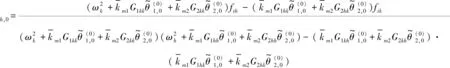
(40)
当ν=1,由式(6)可得脱齿函数的傅里叶级数表达式为
(41)
第κ阶模态振幅脱齿边界取决于ςk,0、ςh,0和系统模态振型。由式(40)中ςk,0和ςh,0的表达式可见,传动转矩、平均啮合刚度、脱齿函数共同决定着模态振幅的脱齿边界。
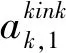
(42)
利用式(38)的幅频响应表达式和式(36)、式(40)、式(41),给定一个模态响应幅值ak,0,即可得到响应的啮合频率ωm,进而得到机构在第k阶模态主共振区域内的幅频响应曲线。图4(a)为同伦法所得从动齿轮幅频曲线。与多尺度法和数值积分结果对比可见,在啮合频率远离固有频率、未发生脱齿的频率范围中,同伦法和多尺度法所得曲线与数值积分的曲线之间的误差很小,且同伦法得到了与多尺度法、数值计算方法一致的脱齿幅值边界。
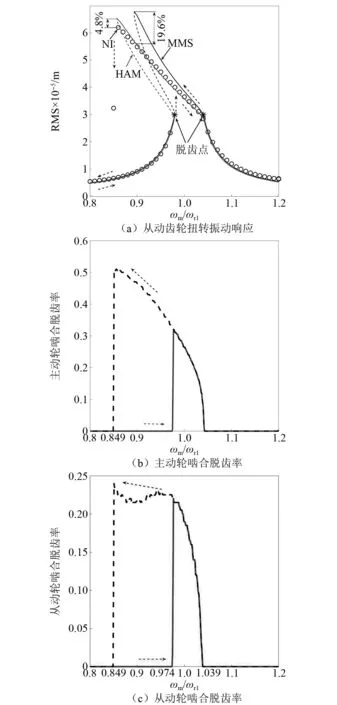
图4 第1阶模态主共振,HAM计算结果对比Fig.4 Comparisons between the HAM and NI for primary resonance in the first mode
对照图4(b)、图4(c)中的脱齿率曲线可见,多尺度法所得幅频曲线与数值积分结果之间的偏差,随着脱齿率的增大而增大。将某一啮合频率处的模态振幅间的差值定义为不同算法间的误差。如图4(a)所示,多尺度法、同伦法所得幅频响应曲线的最大幅值分别为67.8 μm、65.3 μm,对应啮合频率处的数值积分结果分别为56.7 μm和62.3 μm。以数值积分的结果为参照,多尺度法和同伦法对应的相对误差分别为19.6%和4.8%。由于多尺度法依赖于脱齿率较小的假设,此处主动轮啮合处的脱齿率超过了40%,导致多尺度法的误差较大,而同伦法仍能具有较高的计算精度。
图5(a)中为各方法所得中间齿轮第二阶扭转模态主共振幅频曲线对比,图5(b)、图5(c)展示了相应的脱齿率曲线。与图4中结果所得结论相同,以数值计算结果为参考,随着脱齿率的增大,多尺度方法的计算精度降低,而同伦法仍能保持较高的计算精度。
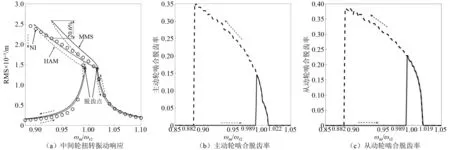
图5 第2阶扭转模态主共振,HAM结果对比Fig.5 Comparisons between the HAM and NI for primary resonance in the second mode
2.2 亚谐共振ωm≈2ωk
对于ωm≈2ωk,参照主共振中的同伦推导过程,即可得到亚谐共振的幅频关系式为
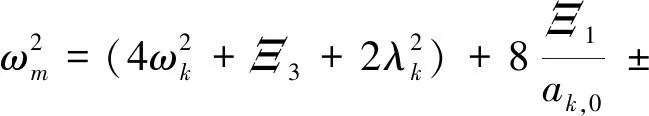
(43)
由幅频响应表达式可见,亚谐共振响应同样与阻尼λk和Ξ1,2,3关系密切。Ξ1中体现着平均啮合刚度与脱齿函数Θ第1阶谐波成分的作用;Ξ2则体现出时变啮合刚度的作用;Ξ3则体现出平均啮合刚度、脱齿函数Θ第0阶和第2阶谐波成分的作用。
图6、图7分别对比了同伦法、多尺度法和数值积分前两阶扭转模态亚谐共振的幅频响应曲线。其中,虚线为不稳定解分支,两条垂直线标定着系统的不稳定边界。幅频响应曲线在出现脱齿前保持垂直。出现脱齿现象后,原本垂直的两条幅频响应曲线向左倾斜。与主共振情况相似,较低的分支为不稳定解,而另一分支为稳定解。

图6 第1阶扭转模态亚谐共振,HAM计算结果对比Fig.6 Comparisons between the HAM and NI for sub-harmonic resonance in the first mode

图7 第二阶扭转模态亚谐共振,HAM计算结果对比Fig.7 Comparisons between the HAM and NI for sub-harmonic resonance in the second mode
由图6和图7可知,以数值计算结果为参照,同伦法比多尺度法可以在更高的脱齿率范围内保持计算精度,这是因为同伦法不依赖于任何小变量。
2.3 超谐共振ωm≈1/2ωk
考虑时变啮合刚度的前两阶谐波成分,依照与主共振相似的同伦法推导过程,即可得到超谐共振ωm≈1/2ωk时的幅频关系式
(44)
其中,
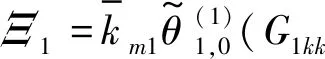
系统亚谐共振响应同样与阻尼λk和Ξ1,2,3关系密切。Ξ1中体现着平均啮合刚度与脱齿函数Θ第1阶谐波成分的作用;Ξ2则体现出时变啮合刚度第二阶谐波成分的作用;Ξ3则体现出平均啮合刚度、脱齿函数Θ第0和第2阶谐波成分的作用。
图8中对比了超谐共振ωm≈1/2ωk同伦法与数值积分所得幅频响应曲线。图中实线为数值积分所得曲线,圈线为同伦法所得曲线。
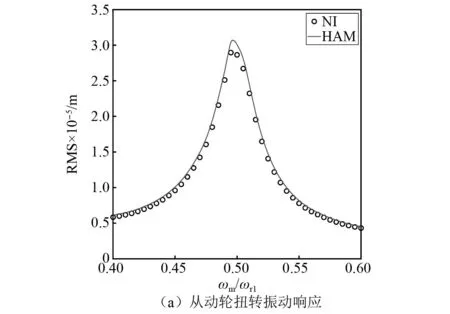
图8 超谐共振,HAM计算结果对比Fig.8 Comparisons between the HAM and NI for super-harmonic resonance
由图8可知,当啮合频率接近前两阶扭转固有频率1/2时,幅频响应曲线的顶部向左轻微倾斜,说明系统发生了轻微的脱齿现象。同伦法与数值积分所得幅频响应曲线达到了很好的一致,同伦法同样适用于计算齿轮系统超谐共振响应。
3 结 论
(1) 考虑时变啮合刚度、脱齿、各级齿轮啮合间的耦合关系,建立了二级直齿传动机构的刚柔混合模型,通过同伦法一阶变形公式,推导得到了二级齿轮系统主共振、亚谐共振和超谐共振的幅频关系表达式。
(2) 同伦法可适用于求解含有间隙非线性因素的,多自由度齿轮机构的共振、亚谐共振和超谐共振等非线性响应,能够准确预测脱齿发生的啮合频率、刚度“软化”等。
(3) 与多尺度法相比,同伦法推导过程不依赖于任何小变量,因而在脱齿率较高时,以数值积分结果为参照,同伦法具有比多尺度法更高的计算精度。本研究为复杂齿轮传动机构的非线性动态特性分析提供了更为精确的理论分析方法。
