基于IMSGP-WEDI的水电机组故障预警方法
2024-04-29曹超凡李明亮蒋双云张广涛李中梁
曹超凡, 李明亮, 蒋双云, 张广涛, 李中梁, 卢 娜
(1. 郑州大学 水利与交通学院,郑州 450001; 2. 华电电力科学研究院有限公司,杭州 310030;3. 润电能源科学技术有限公司,郑州 450052)
水电机组实际运行过程中各种工况转换频繁,加之受到水力、电气、机械等多方面综合因素影响,可能产生多种故障,因此需开展机组状态趋势预测,以掌握机组实时运行状态,及时发现机组运行异常和早期故障,并据此制定合理的检修计划,避免发生重大事故[1-2]。
水电机组状态趋势预测是利用机组历史监测数据进行学习构建趋势预测模型,并基于当前机组运行数据实现未来机组运行状态的预测[3-4]。在实际运行中,水电机组故障通常在振动信号上有所体现,提取水电机组振动信号的重要特征进行机组状态趋势预测,可以有效反应机组真实运行状态,并实现故障预警[5-6]。
目前专家学者针对旋转机械开展故障预警研究已经取得一定进展。鹿卫国等[7]假定水电机组正常状态下历史振动数据服从某一概率分布,将偏离概率分布的数据归类为故障状态实现故障预警。安学利等[8]利用最小二乘支持向量机构建三维曲面预警模型,通过对机组实时运行振动数据进行状态评估实现故障预警。刘涛等[9]利用多元状态评估技术对电厂风机观测向量进行最优估计,从而得到估计向量,通过计算观测向量与估计向量之间的偏离度,判断是否超过预警阈值,从而实现风机的实时故障预警。然而,现有的预警方法多存在预警指标特征信息单一,所构建预警指标难以完全表征机组状态,早期预警困难的问题。而利用振动信号中的多元特征构建综合预警指标,可以更加有效地判断机组健康状态。为此,刘东等[10]通过计算水电机组振动信号时域特征与健康值之间的相对差值作为时域劣化指标,计算实测信号频域特征向量与健康聚类中心之间的欧氏距离作为频域劣化指标,实现了水电机组劣化在线评估。Mao等[11]提出一种具有交替最小化方案的算法进行张量表示和无监督特征提取,并利用提取的特征构建健康指标来进行地铁车轮劣化状态评估。Liu等[12]利用深度卷积神经网络提取轴承退化数据与正常数据之间的特征距离构建演化状态指标,然后利用无监督聚类方法划分状态阶段,实现轴承早期故障演化监测。尽管如此,利用综合指标实现机组早期故障预警的研究仍然较少,且当前研究中大多使用单传感器振动数据作为模型输入,其所提取的特征信息远不如多源数据的全面,并且容易遗漏重要特征。
针对上述问题,并考虑到遗传规划(genetic program,GP)可以更有效地构造表征机组状态的高级特征,进而获得更为可靠的预警结果,且目前其在故障预警领域应用较少,本文提出了基于集成多传感器遗传规划(integrated multi-sensor genetic programming, IMSGP)与权重欧式距离指标(weighted euclidean distance index, WEDI)的水电机组故障预警方法。本文主要工作为:
(1) 融合多传感器信息,引入GP算法,构建了IMSGP故障预警模型,可更加全面地反映机组运行状态。
(2) 综合考虑时频特征信息构建多元原始预警特征集,利用复合检测指数(composite detection index,CDI)进行特征选择,剔除无关特征向量,提高了特征敏感性,降低了后续算法的复杂性。
(3) 结合主成分分析(principal component analysis,PCA)[13]与欧式距离[14]构建WEDI综合预警指标,以偏离健康状态权重欧式距离系数3倍偏差为预警阈值,实现水电机组早期故障预警。
(4) 利用所提出的方法对水电机组实测信号进行处理,结果表明,所构建的状态趋势预测模型能够及时发现水电机组状态变化,预警时间比明显出现症状的时间提前6天左右。
1 基本理论
1.1 遗传规划
遗传规划是遗传算法与计算机编程相结合的一种进化方法[15],具有利用候选解表示的动态结构和全局搜索的特点,但与其他进化算法不同的是,GP采用更灵活的层次模型(树)来表示解空间,其结构和大小可自适应调整,更适合于表示复杂问题[16]。GP中的个体通常由函数集和终端集组成。GP的函数集可分为一般函数(如+,-,×,÷等)、逻辑函数(如if,and,or等)和其他数学函数(如exp,sin,cos等)。终止符集通常为变量和特征等。如图1所示,该树模型是GP的一个个体,数学上可以表示为[8×(x+5)]-(3÷y),其中+、-、×和÷包含在函数集中,终端集包含x、y、8、3和5。在水电机组故障特征构造中,该方程可作为所构造的高级特征,其中,x和y为水电机组信号的两个原始特征。由此可以看出,GP算法具有很好的可视化和模型解释能力。此外,GP算法树深度可以根据实际问题进行调整,模型复杂程度与问题复杂程度相关。
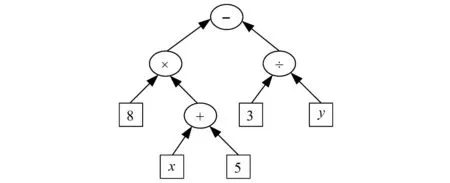
图1 某个体树形GP结构表达Fig.1 Tree structure representation of some individual in GP
GP算法的流程图如图2所示,主要包含:创建初始个体、个体适应度评价、选择、交叉、变异、判断是否满足终止条件,结束。其中选择指GP算法中个体的选择与复制操作,其遵循生物界的“优胜劣汰”原则,目的是保留种群中优秀的个体,淘汰劣质个体,根据适应度函数值,选择复制上一代优秀个体,保证下一代个体更优秀;交叉指选择父代中的两个个体,相互替代他们的部分结构,从而产生两个新的个体,该操作是为了使不同个体的信息相互交换,丰富种群的多样性,根据适应度值与被选定概率成正比的关系,随机选择父代个体,也可以通过随机选择父代树节点作为交叉节点,以交叉点为根的整个子树为交叉段,两个子树相互交换,产生新的树结构;变异指GP个体的变异,包含对终止符集和函数符集进行变异操作,变异位置是随机选择父代树的任一节点,对于原位置任意替换,当变异点为函数符集,则替换前后运算数目元素相同。
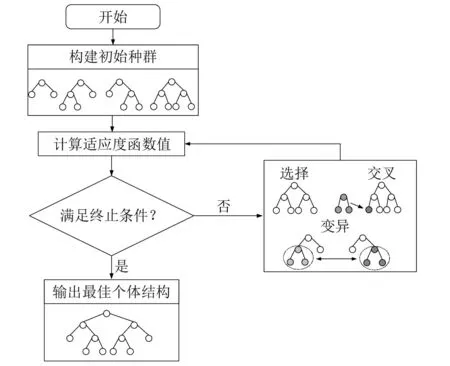
图2 遗传规划算法流程图Fig.2 Genetic programming algorithm
1.2 时频域特征
对于预处理后的多元水电机组信号,需提取其基础特征信息作为后续IMSGP模型的输入。本文选取了15个时域特征和13个频域特征进行基础特征信息提取。
时域特征分别为算术平均值、平均幅值、方差、标准差、方根幅值、均方根值、最大值、最小值、峰值、峰值因子值、峰度值、波形因子值、脉冲因子值、边际因子值和偏度值。时域特征计算式如表1所示,其中,v(i)为信号样本点,N为样本点数。

表1 时域特征参数Tab.1 Time domain feature parameters
频域特征考虑了信号的频率特性,通过对信号进行快速傅里叶变换(fast Fourier transform, FFT)[17]得到的频谱幅值进行计算,提取出信号的频率特性,13个频域特征为:平均频率F1、标准频率的偏差F2、频率中心F3、均方根频率F4、主波段的位置变化特征F5和F6、频谱的集中或分散程度特征F7~F13。计算公式如表2所示,其中,s(i)为原始信号的频谱,M为谱线数,f(j)为第j条谱线的频率值,Aj为第j条谱线的幅值。
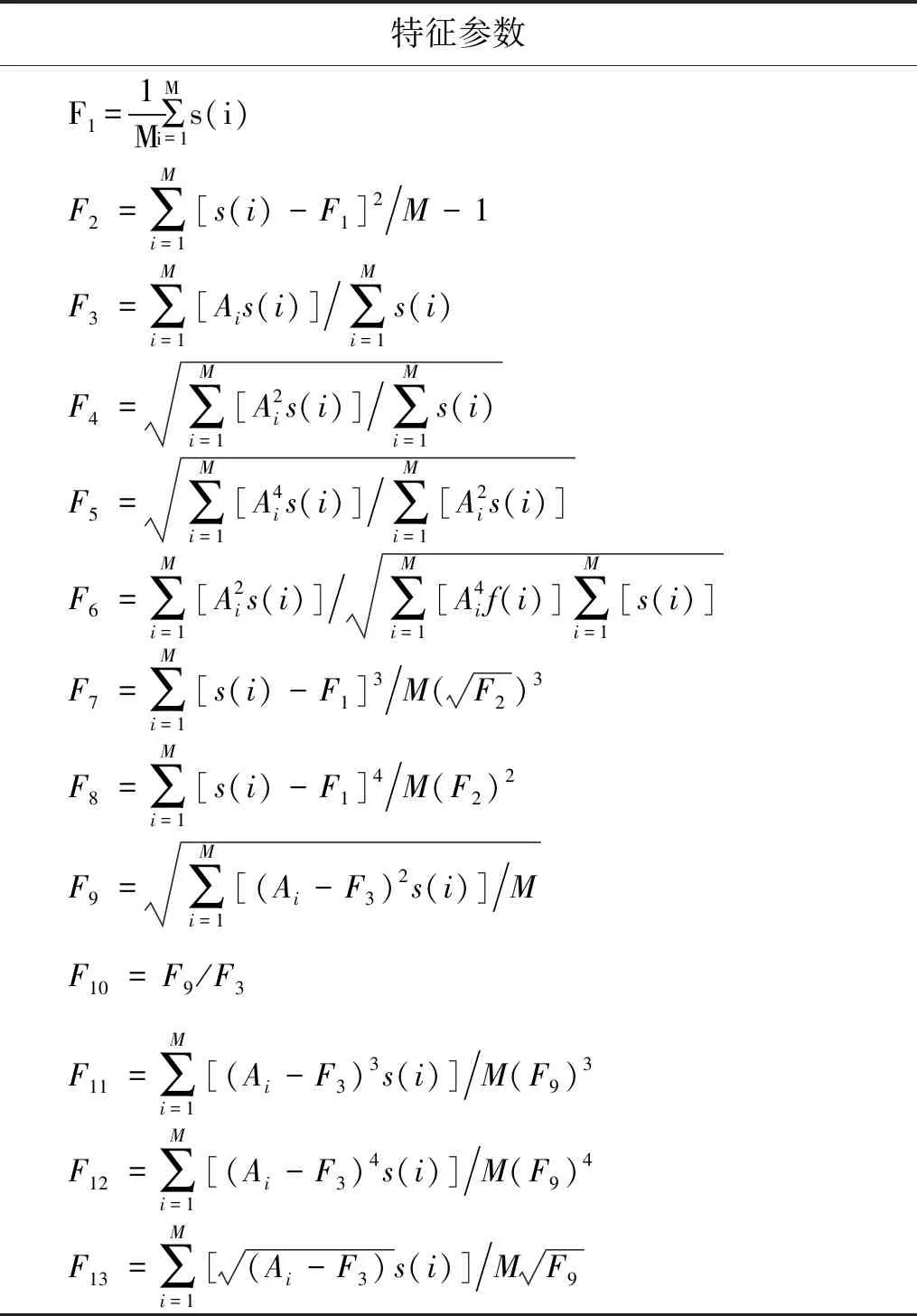
表2 频域特征参数Tab.2 Frequency domain feature parameters
2 基于IMSGP-WEDI的水电机组故障预警方法
2.1 复合检测指数
从多传感器信号中能够获得大量的特征信息,但其中不乏冗余的无用特征,为了提高计算信号特征的性能,降低后续GP的计算复杂度,本文利用复合检测指数CDI作为特征选择的敏感特征评价指标,将进行多元原始信号特征集特征筛选。CDI的计算步骤为:
步骤1计算检测指数DI值
假设Ni,Nj分别是由旋转机械状态i和状态j的信号计算得到的时频域特征值,且服从正态分布。则状态i和状态j下某一特征值的DI[18]值为
(1)
式中:σi,σj为Ni,Nj的标准差值;μi,μj为Ni,Nj的平均值。
步骤2计算CDI值
由式(1)可知,故障样本的类间间距越大,类内间距越小时,对于故障分类越有利。因此,DI值越大,越容易识别出对应的两种不同状态样本的差别,据此,本文构造CDI为
(2)
式中:n为故障类型的种类数; DIi,j为状态i和状态j对应特征的DI值。
可见,CDI综合考虑到不同故障类型,同一特征值计算得到的DI平均值与最小值。CDI越大,表明该特征对所有故障类型的敏感性越高。
2.2 集成多传感器遗传规划
考虑到将多传感器数据输入GP后,在各设定优化参数不变的前提下重复运行GP模型,其输出的结果会有差别,利用其进行后续的预警指标构建得到的预警结果有优有劣,即多传感器遗传规划(multi-sensor genetic programming, MSGP)运行结果不稳定,鲁棒性不强,因此本文引入集成化思想,构建了集成多传感器遗传规划IMSGP模型,这里的集成是指通过重复运行MSGP得到高维高级特征集合,即假设集成k次,就会得到k个互相独立的一维高级特征,也就是k维高级特征。这样,所得的k维高级特征就可以输入到PCA算法进行降维处理,获得低维敏感特征,提高模型的泛化性能及水电机组故障预警的效率。
2.3 IMSGP目标函数
GP中目标函数值反映了种群个体的特性,在优化程序运行时,常常通过目标函数评价来寻找最佳个体。而当训练样本数量较少时,GP构造的特征在训练集上容易获得较好的分类性能,但在测试集上可能会产生过拟合的现象。为了解决这一问题,本文构建了一种融合分类精度和样本距离的遗传规划适应度函数,其计算公式如式(3)所示,利用最小-最大归一化方法将Fitness变换到 [0,1]范围内。
(3)
式中:Acc为构造特征的分类准确率,通过k-fold交叉验证计算得出,在本文计算中取5折[19]; Dist为距离度量,其原理是使样本的类内距离最小,类间距离最大,以此来降低同类样本的差异性同时提高构造特征的鉴别能力。Dist计算公式如式(4)~式(5)所示,其计算基础是两个样本特征的JS(jensen-shannon)散度值[20],同类样本之间的距离计算公式如式(4)所示,类间样本之间的距离计算公式如式(5)所示,最后受sigmod函数的启发,利用式(6)对距离进行归一化处理,保证式(3)处于[0,1]范围内。
(4)
(5)
(6)
式中:Din为类内距离;Dout为类间距离;Ni,Nj为水电机组运行状态i,j下的特征个数;X为IMSGP构造的高级特征。
2.4 故障预警指标
为及时发现水电机组早期故障,本文结合PCA算法与欧式距离构建一种权重欧式距离故障预警指标,其流程如图3所示,具体步骤为:
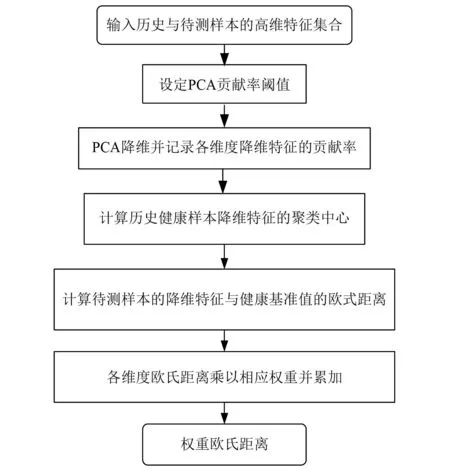
图3 权重欧式距离计算流程Fig.3 Weighted Euclidean distance calculation procedure
步骤1设定PCA算法贡献率阈值,将贡献率达到阈值的前z个指标提取出来,从而将高维故障特征集合降到z维度,并记录降维特征的贡献率。
步骤2计算健康状态下历史信号降维特征的聚类中心,并将其作为健康基准值。
(7)
式中:z为降维故障特征集合的维度;n为健康状态下历史信号样本;X为降维后特征值;H为健康基准值。
步骤3计算水电机组待测信号特征与健康基准值之间的欧式距离。
步骤4将步骤3得到的欧氏距离与步骤1中相应的贡献率相乘并累加,得到最终的故障预警指标。
(8)
式中:N为待测信号样本数;w为z维故障特征对应的贡献率,WED即为所求权重欧式距离。
2.5 故障预警方法流程
本文所提出的水电机组故障预警方法流程如图4所示。具体步骤为:
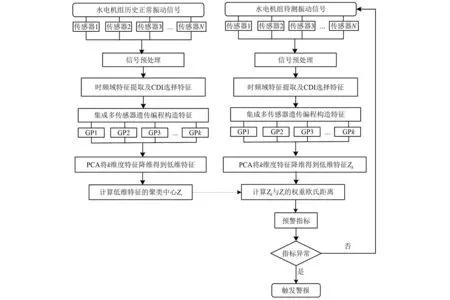
图4 基于IMSGP-WEDI的水电机组故障预警方法流程Fig.4 Fault early warning process of hydropower unit based on IMSGP-WEDI
步骤1获取水电机组历史正常状态信号和待测信号多传感器数据,利用小波阈值降噪[21]方法对振动信号进行预处理。
步骤2提取预处理后信号的时频域特征,并进行CDI特征选择。
步骤3已经CDI选择后的特征参数为输入变量,以式(3)为目标函数,进行集成多传感器遗传规划,得到由多个高级特征表达的高维特征向量。
步骤4设定PCA降维阈值,利用PCA将高维特征向量映射到低维空间,得到代表水电机组运行状态的融合特征向量。
步骤5以正常运行状态下信号数据融合特征向量的均值作为聚类中心,并计算正常状态数据融合特征与聚类中心的权重欧式距离标准差。
步骤6以三倍标准差为预警阈值,将第一次超过报警阈值所对应的数据定义为预警样本,并在此时触发报警。
3 水电机组实测信号故障预警分析
3.1 数据概况及预处理
水电机组的结构如图5所示,主要包括一个发电机、一个水轮机、上下机架、三个导轴承和一个推力轴承,发电机与水轮机的轴通过法兰连接。
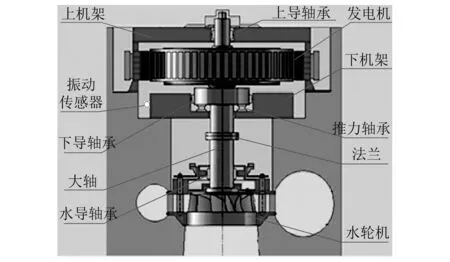
图5 水电机组结构图Fig.5 Hydropower unit structure
在运行过程中,工作人员发现电站3号机组出现严重振动,经专业人员排查,得知该故障是由水力不平衡因素引起。数据来源于安装在上导轴承、推力轴承和水导轴承上各个方向的9个振摆数据和7个工况数据(包含水头、导叶开度等)共16个传感器数据。机组停机检修前,先后经历了正常、故障预警、故障三种状态。
本文选取三种不同状态下水电机组的信号样本进行训练,采样频率为458 Hz,采样点数为2 048,每类数据包含20个样本,其中训练样本每类状态下取5个,共15个,测试样本每类状态下取15个,共45个,预处理后的信号样本经过特征选择后输入IMSGP模型中运行20次。振动信号样本时序波形(以水导轴承x向摆度传感器、上导轴承x向摆度传感器和上导轴承y向摆度传感器为例)如图6所示。
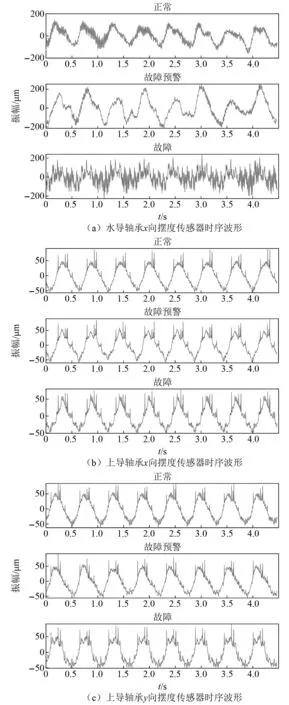
图6 水电机组部分传感器时域波形图Fig.6 Partial time series waveforms of hydropower generating unit
根据机组状态将信号数据划分为历史数据和待测数据。
(1) 历史信号数据
采集水电机组健康状态下多传感器信号作为历史数据计算预警阈值,共有253个数据样本,每个样本包含4 096个数据点。
(2) 待测信号数据
采集故障发生前后机组多传感器信号作为待测数据,采集时间为2015-08-15—2015-08-28,共有375个数据样本,每个样本包含4 096个数据点。
采用小波阈值降噪方法对振动信号数据进行预处理。小波阈值降噪方法的参数设置为:小波分解层数设定为3层,阈值选择方法为“sqtwolog”方法,阈值处理方法为软阈值方法,阈值缩放方法为“mln”方法,小波基函数为“DB4”小波。
3.2 IMSGP构建高维特征向量
IMSGP参数设置如表3所示,计算16个传感器数据的时频域特征,得到448维特征集合,各个特征对应的CDI值如表4所示,选择每个传感器中的CDI值较大的前6个特征,得到96维特征,其对应的CDI值如表5所示。

表3 IMSGP参数设置Tab.3 IMSGP parameter setting
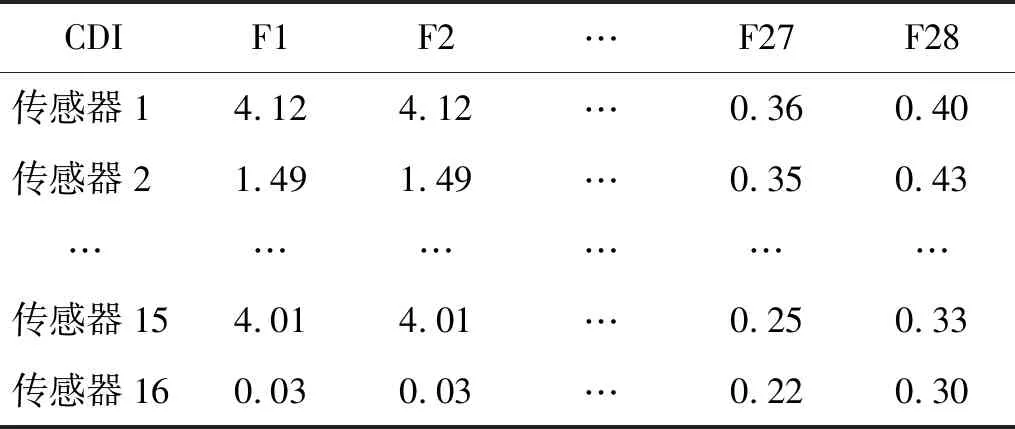
表4 高维特征集的复合检测指数值Tab.4 The CDI of high-dimensional feature set
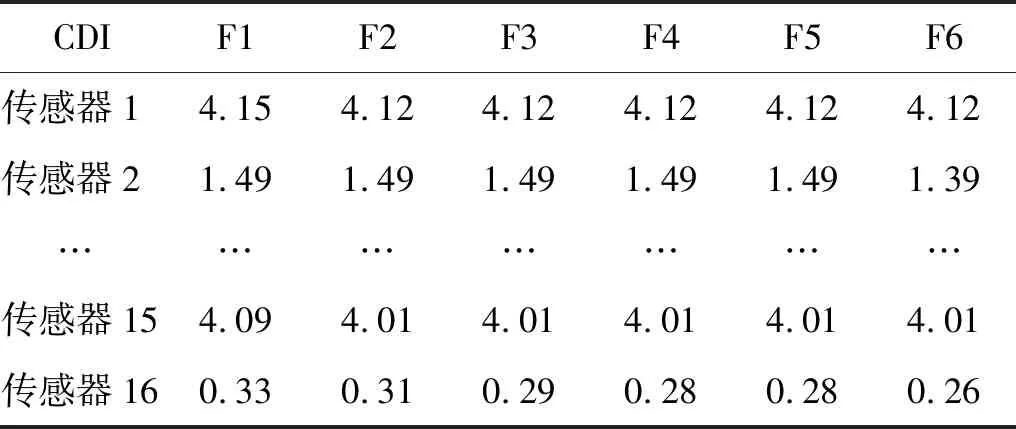
表5 特征选择后对应特征的CDI值
将所得96维时频特征作为遗传规划的函数集,训练IMSGP模型,其所得高维特征集合如表6所示。
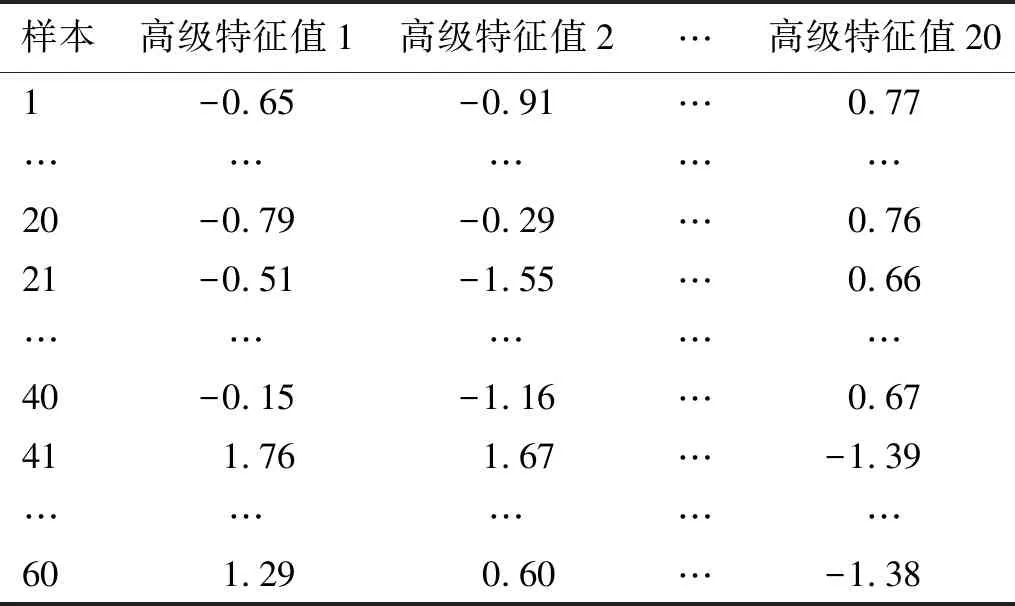
表6 IMSGP所得历史数据的高级特征向量集
将待测信号样本输入到训练完成的IMSGP模型中,得到待测数据样本的高维特征集合,如表7所示。
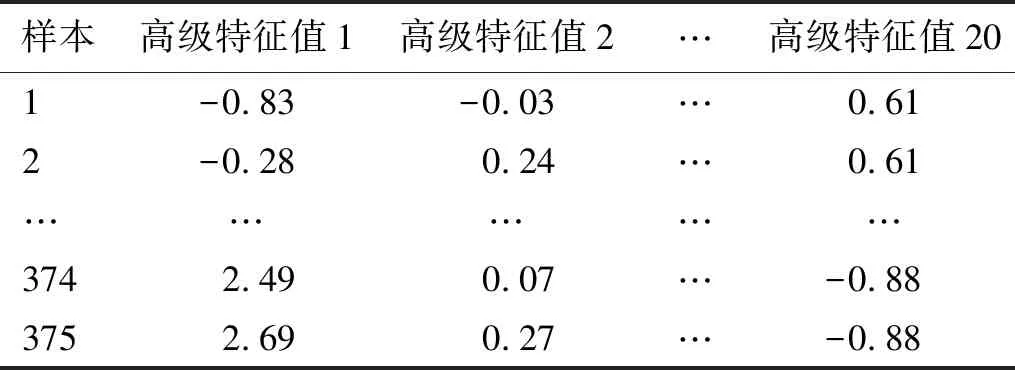
表7 IMSGP 所得待测数据的高级特征向量集
3.3 权重欧式距离计算
设定PCA降维特征贡献率为0.95,利用PCA算法对待测信号样本的高级特征进行降维处理,降维特征贡献率如图7所示。由图7可知,前两个特征的贡献率依次为0.747 0和0.235 8,累计贡献率为0.982 8,超过所设定阈值0.95,因此,将原来的20维度特征向量降低到2维,其特征值如表8所示,记录这两个特征的贡献率值作为后续权重欧式距离的计算权重。根据权重欧氏距离计算方法,选择表8中前50组正常状态下融合特征的平均值作为健康状态基准值,计算待测样本与健康基准值的权重欧氏距离并作为故障预警指标值。
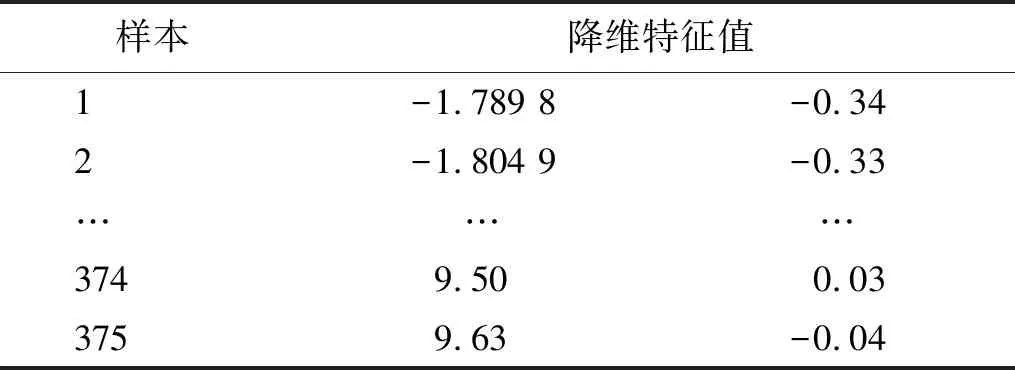
表8 经PCA降维后的高级特征值Tab.8 High-level feature values after PCA
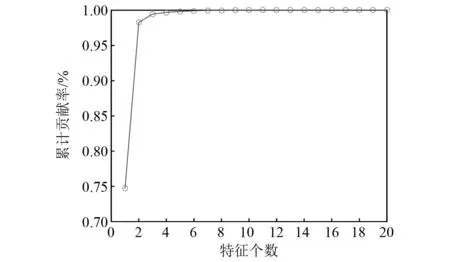
图7 高级特征对PCA算法的累计贡献率Fig.7 Cumulative contribution rate of high-level features to PCA
3.4 预警阈值计算
经过IMSGP特征提取与PCA降维后,将得到的权重欧氏距离数据减去其均值进行归一化处理,使预警指标从0开始,计算健康状态下253组数据的融合特征与健康基准值之间权重欧氏距离的标准差,通过计算,得到正常状态下253组数据的融合特征与健康基准值之间的标准差为0.315 8,三倍标准差为0.947 3,即为故障预警指标的阈值[22]。
3.5 待测样本预警分析
将待测样本对应的故障预警指标值与预警阈值绘于同一张图上,如图8所示,由图8可知,在08-15—08-20,机组预警指标一直稳定在较低水平,而且波动微乎其微;在08-22左右机组振动预警指标首次突破阈值,可认为在该时段内机组开始产生故障,将发出预警。通过与运行管理人员沟通交流得知,在08-15—08-20,机组振动及各项参数值均处于正常水平,无明显波动;根据电站的事后分析报告,发现机组在08-28开机过程中,上机架和水轮机蜗壳及尾水管等处异常声音明显,通过检修发现是由水力不平衡故障引起的。可以看出,利用所提出的预警方法得到的结果表明机组早在08-22前后就出现了故障趋势,因此本文提出的故障预警指标能够有效反映水电机组的运行状态并实现机组故障预警,对保证机组和电站安全具有实际应用意义。
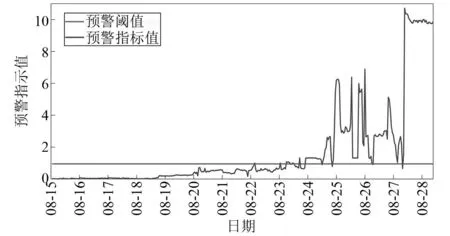
图8 水电机组故障预警指标计算结果Fig.8 Calculation results of fault early warning indicators
3.6 对比试验
为进一步证明本文方法的有效性,本文针对图4所示方法流程中的多传感器数据输入以及IMSGP步骤设置两组对比试验,即:
(1) 单传感器试验
单传感器试验与本文方法不同的是:在2.5节流程的步骤1中利用单传感器数据输入代替多传感器输入,相应的步骤3中以集成单传感器GP代替IMSGP,即通过重复运行单传感器GP模型得到高维高级特征集合。其余步骤与本文方法相同。
(2) 无集成试验
无集成试验与本文方法不同的是:在2.5节流程的步骤3中以MSGP代替IMSGP,另外由于只运行MSGP模型一次,得到的一维高级特征可直接进行故障预警指标计算,无需进行PCA降维,所以不进行步骤4的操作。其余步骤与本文方法相同。
如图9所示,图9(a)、图9(b)、图9(c)分别为三个单传感器数据所得试验结果,可以看出图9(a)、图9(b)两图结果基本无法反映机组状态从正常到故障的劣化过程,预警阈值无法起到作用,图9(c)所示结果基本与本文方法的结果接近,在08-23左右首次突破阈值,但其早期故障征兆不如本文故障预警指标明显,说明多传感器输入可以考虑到更多有效特征;图9(d)、图9(e)、图9(f)为无集成情况下试验结果,因为GP算法本身稳定性不强,可以看出,图9(d)、图9(e)所对应的两组试验无法得到有效的结果,只有图9(f)所示结果与本文结果相近,说明不集成时结果优劣难以预测,而通过集成可以得到更加稳定和准确的结果。
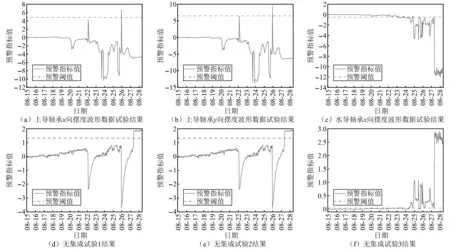
图9 单传感器和无集成对比试验Fig.9 Signal sensor and no integrated comparison experiment
4 结 论
本文将集成多传感器遗传规划方法应用到水电机组状态趋势预测中,结合PCA算法与欧氏距离构建了水电机组故障预警指标。通过对水电机组多传感器数据进行试验,分别利用历史数据与待测数据进行模型的训练与测试,试验结果表明本文提出的基于IMSGP与WEDI的水电机组故障预警方法能够有效发现早期故障,并进行及时预警。
