薄板件高精度测量线激光连续扫描路径规划*

徐诚智,赵文政,刘银华

(上海理工大学机械工程学院,上海 200093)

0 引言

线激光测量是实现自由曲面高精度测量的重要手段。通过安装在六自由度机械臂末端的传感器对三维复杂结构曲面进行关键测点测量,其检测规划问题可以抽象为三维覆盖路径规划问题(3D-coverage path planning,3D-CPP)。

覆盖路径规划旨在避开规划区域中障碍物的前提下,规划一条以最小的路径代价通过所有关键点或任务区域的路径[1]。根据规划场景可划分为:二维平面、三维平面和三维自由曲面下的路径规划。根据规划特点可划分为:离散型和连续型路径规划。

针对二维离散型覆盖路径规划问题:KAFKA、PAPADOPOILOS等[2-3]提出了RITA和RITACSP算法,通过更少的迭代次数得到最优路径。针对三维平面的覆盖路径规划问题:石础等[4]为解决检测工艺可靠性问题,提出了一种Z字形(光栅)覆盖路径规划方法。ZHU等[5]提出了Glasius生物启发神经网络(GBNN)算法,实现AUV在非结构化环境中的自主避障。然而,上述方法难以实现关键测点全覆盖路径规划。

针对三维自由曲面覆盖路径规划问题:GLORIEUX、WEI等[6-8]提出的规划算法,将路径覆盖问题抽象为旅行商问题(traveling salesman problem,TSP)与下一最优视点问题(next best viewpoint,NBV),对路径进行离散型规划。WANG等[9]提出的算法能够通过分布优化有效缩短路径长度。HAMEED等[10]提出了一种边对边方法,能够有效避免路径重叠并提高覆盖率。TAE等[11]提出的算法,能够在有效提高路径平滑的同时实现场景全覆盖。UTKARSH等[12]提出了一种基于萤火虫群优化的规划方法,有效降低了路径成本。

然而上述方法仍然是基于测点采样的离散式路径规划方法。LI等[13]针对CMM测量,提出了一种连续覆盖路径规划方法,提高了测量稳定性和效率。但仅用于接触式测量场景。

在使用线激光对复杂结构三维自由曲面进行面向精度的测量过程中,上述覆盖路径规划方法存在以下3个问题:首先,难以同时保证测量结果精度和测点覆盖率;其次,大多数方法通过求解TSP问题来实现覆盖路径规划。然而,在线激光传感器连续逐行扫描、单帧数据呈直线分布的特点下,这种方法会造成扫描精度降低、路径可行性不足等问题;最后,现有方法忽略了测量位姿对于扫描精度的影响。

针对上述问题,本文提出了一种基于搜索随机树策略与路径生长策略融合的3D-CPP方法,旨在通过路径规划实现测量精度的优化。具体而言,该方法通过使路径围绕被测型面逐步生成,实现测量对象上关键测点的全覆盖路径规划。进一步,基于线激光连续扫描特点,构建了一个以测量不确定度为主兼顾测量效率的路径段评价指标,从而实现检测路径的深度优化。

1 线激光传感器工作特点

1.1 连续扫描

线激光传感器是一种广泛用于精度测量、点云重建等非接触式光学传感器。在自动化测量工艺中,一般将测量传感器安装于机械臂末端,机械臂通过执行经过规划的扫描路径来完成测量过程。线激光传感器执行扫描任务时,会将呈直线分布的激光簇投射到被测物体上,其反射光线被CCD摄像头捕获并检测(如图1所示)。传感器在扫描过程中,以高采样频率(100～5000 Hz)不断进行数据采集,因此可以视作一个连续工作的传感器;线激光传感器所采集的单帧数据以直线分布的形式呈现,并非在一个矩形视场内采集数据,这与蓝光相机等单帧采集矩形视场内被测件表面数据的传感器存在明显差异。因此,在进行全覆盖路径规划时,如果采用离散型路径规划方法,线激光传感器将无法全面有效地采集扫描路径上的关键测点,从而导致路径的可行性下降、采样结果精度下降以及路径执行效率降低等问题。

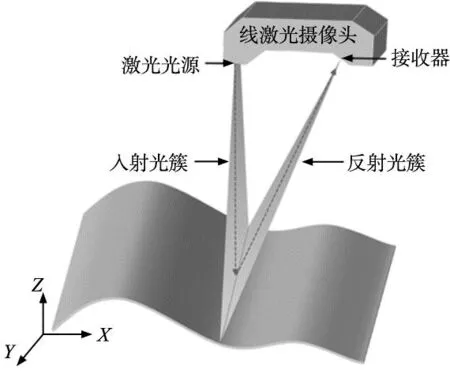
图1 线激光自由曲面扫描示意图

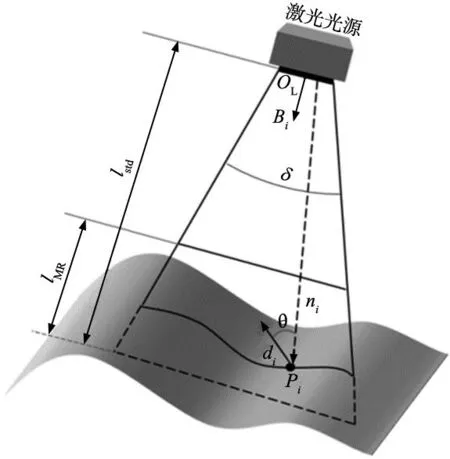
图2 光学约束原理图

1.2 线激光传感器的光学约束

由机械臂主导的自动化线激光测量,其执行机构的硬件系统主要包含六自由度(6-DOF)机械臂、工装夹具以及线激光摄像头(后简称“线扫相机”)。在规划测量路径的过程中,生成最优路径时会考虑各种光学约束,主要包括视角、测量范围(MR)和视野(FOV)范围[14]。

(1)视角约束。入射激光矢量与被测点法向矢量夹角应小于摄像头的最大视角γ。

ni·di≥cos(γ)

(1)

(2)

式中:ni为采集第pi个测点的激光矢量方向,di为第pi个测点的法向矢量,L为光源位置,Pi为第pi个测点的位置。

(2)测量范围约束。测点应处在距离激光光源规定的可视范围内。

(3)

式中:lstd为光源到视野最远位置的直线距离,lMR为传感器测量间距,及视野最近位置到视野最远位置的直线距离。

(3)视野(FOV)约束。测量对象应处于激光簇照射范围内。

(4)

式中:Bi为传感器中心位置的光源的矢量方向,δ为视野范围角。

1.3 传感器位姿引入的测量不确定度

不确定度是一种用于评估测量质量与表达测量结果不确定性的可量化指标,即测量结果在多大程度上能够准确表征被测属性的值。线扫相机进行复杂结构薄板件全型面上关键特征点检测时,由于传感器位姿不断变化,其线激光簇的方向矢量与自由曲面上相应被测点的法向矢量之间存在一定的空间夹角θ(偏离角)。当偏离角大于一定阈值后,随着角度的增加,测量结果精度将随之下降直至无法有效测量[12]。因而,本文通过偏离角θ对不确定度进行表征并作为路径规划的主要优化参数。

2 连续全覆盖路径规划

本文提出一种基于搜索随机树策略的覆盖路径规划算法(coverage growing random tree,CGRT)。首先,将被测量对象的三维点云数据和特征点集合作为输入,以最小化测量不确定度为主要目标,建立多目标优化模型;然后,利用局部路径规划方法获得优化模型下的最优子路径;最后,通过全局路径规划方法获取覆盖整个表面的完整测量路径。

2.1 多目标路径优化函数

通过将当前被测物体全型面上的所有n个待测特征点pi纳入集合ψ:{p1,p2,p3,…,pn},得到关键特征点集合ψ。其中每个特征点pi均包含相应的坐标信息和法向矢量信息,即pi(bi,βi)。根据约束式(1)～式(4)所建立的多目标优化函数F如式(5)所示。

F(pj,pj-1,pj-2,α)=ω1*f1(βj,α)+ω2*f2(pj,pj-1)+

(5)

(6)

式中:f1为基于测量偏离角θ(即光线入射角与测点矢量的夹角)的不确定度指数,也是主要的优化子函数;f2为路径长度优化子函数,用于评价所生成的扫描路径长度对测量结果的影响;bj为路径在生长方向对应轴的投影长度,f3为路径转角优化子函数,用于评价相邻两段路径的夹角(路径转角)对测量结果的影响;vectj为第j段路径的方向矢量。

式(7)用于计算表征不确定度的偏离角θ对测量结果精度的影响。

(7)

式中:α为当前时刻,传感器位姿所决定的光线入射方向矢量;βj为当前扫过的测量区域内,第j个测点pj的矢量方向;fthre为基于传感器参数的偏离角阈值函数,当偏离角θ小于传感器的最大视角γ时,将偏差计入统计;当偏离角θ大于γ时,则判断当前特征点超出传感器的视野范围。

2.2 随机搜索树策略下的局部路径规划

为了提高规划路径的测量精度,本研究首先采用随机搜索树策略对被测件的局部路径进行规划,范围限定在单步长lstep之内,然后根据2.1节中建立的优化函数(5)获取局部最优路径段。首先,将被测量的自由曲面Φ沿法向矢量方向向外膨胀(膨胀高度h=lMR),得到表征传感器近端视野位置的自由曲面Φ′;之后,根据被测自由曲面的几何特征、当前扫描移动方向以及传感器的测量范围约束选定步长长度lstep∈{lmin,lmax},并由此生成评价空间Ω1以及生长空间Ω2(如图3所示,其中Ω2⊂Ω1);最后,从当前视点vi寻找下一视点vi+1的具体过程如表1所示。

表1 局部路径规划

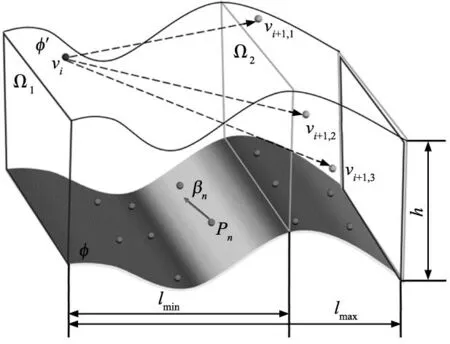
图3 路径规划空间示意图

其中,equaldis sampleVi+1表示等距采样函数,它将生长区间Ω2按照一定间隔进行体素分割,并对每个体素的几何中心位置采集一次潜在最佳视点,最终Ω2内所有潜在最佳视点构成点集{vi+1,1,vi+1,2,vi+1,3,…,vi+1,n}。当前测点集合ψi,i+1是在当前评价空间Ω1与自由曲面Φ相交部分所包含的所有测点的集合。effect featuresψi,i+1表示特征点筛选函数,用于找出当前潜在最佳视点vi+1,k下,测点集合ψi,i+1中所有满足视野约束的特征点ψtmp{pi,pi+1,pi+2,…,pi+s}(ψtmp⊂ψi,i+1)。ψtmp中的测点会输入式(6)的f1中,参与当前局部路径的优化。表1中的步骤4～步骤9,实质上是根据连续测量的特点,对当前路径段扫过的所有测点的不确定度指数等进行累加判断:

(8)

即,根据当前局部路径下ψtmp中所有测点的测量结果,对整条路径段vivi+1进行评价与优化。

2.3 路径生长策略下的全局路径规划

为了保证对复杂结构薄板件进行测量时,被测件表面的所有关键测点能够被有效覆盖,本研究在每次进行局部路径规划后,采用路径生长策略进行全局路径规划。在全局路径规划的过程中,需要整合此前得到的最佳路径段,确定下次局部路径规划的区域以及是否完成路径规划。最终确保传感器能够通过执行最终规划的路径,测量分布于被测件各型面上的所有关键特征点,以提高测量结果的覆盖率和精度(如图4所示)。

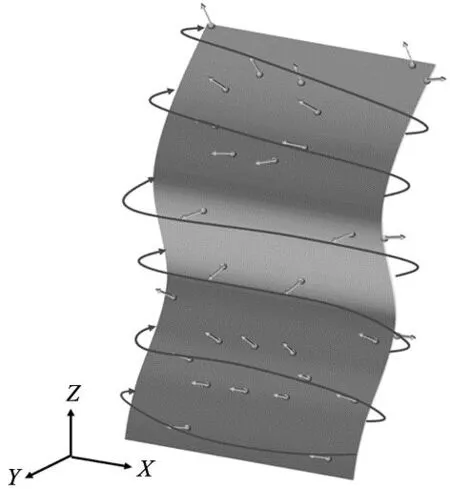
图4 全局规划路径示意图

将被测件点云模型中全型面上所有点的集合定为Γ,其中该被测件自由曲面上的测点集ψ有:ψ⊂Γ。则具体的全局路径规划过程如表2所示。

表2 CGRT全局路径规划

其中,grow direction为生长方向判断函数,它通过输入被测件的点云模型Γ,根据模型自身的几何特点,自动解算出全局路径生长的环绕方向gdirect和攀爬轴向gaxis。如图4所示,一般情况下选择被测件在笛卡尔坐标系Oxyz中,尺寸跨度最大的轴作为攀爬轴(假定为Z轴)。则相应的环绕方向,即是在OXY平面上的顺时针或逆时针方向。grow step函数通过输入被测件的点云模型Γ以及传感器测量间距lMR,计算出每次攀爬的步长gstep。local set函数用于生成局部路径规划空间及相关参数,它根据被测件测点集合ψ以及上述两个函数的输出,求解出当前测点集合ψi,i+1、评价空间Ω1、生长空间Ω2、当前视点vi、光线入射角α,并将参数输入局部路径规划算法(即表1)。

在每一轮规划后,会将当前局部路径与此前规划的局部路径进行首尾拼接,同时将本轮所规划的局部路径上已经覆盖到的测点的集合ψi,i+1剔除出测点集合ψ。当测点集合ψ变为空集时,表示所有测点均被所规划路径覆盖。此时全局规划完成,并得到完整的全局扫描路径G。

3 案例分析

为验证所提出方法的有效性,采用某车型车门总成开展应用验证。车门结构示意如图5a所示。实际使用的车门数模如图5b所示,其最大长度、宽度、高度分别为856.6×79.9×1 151.2 mm,车门表面的灰色矢量的起点为构建的关键特征点的位置,箭头方向表示关键特征点的法向朝向。根据某型号线激光传感器的激光三角采样参数特点,设定关键特征的法向量与传感器位姿矢量的夹角小于90°。该车门包含如孔、槽、切边点、匹配面点等关键特征点4633个,采用线激光传感器对该车门的覆盖路径进行规划。

(a) 车门结构 (b) 实际使用的车门数模

为验证所提出算法效果,与文献[8]的Zigzag型连续路径规划以及基于自组织映射神经网络算法(self-organizing map,SOM)[16]进行对比。案例中线激光传感器相关参数均采用统一数值。其中传感器测量范围lMR=200 mm,光源到视野最远位置的直线距离lstd=400 mm,视野范围角δ=∠30°。针对仿真的车门几何特点,提出的 CGRT算法规划将Z轴正方向作为攀爬方向,将绕Z轴顺时针方向作为环绕生长方向,生长步长gstep∈{100 mm,150 mm}。SOM算法的规划结果最终收敛于第20,346次迭代。3种算法规划后得到的全覆盖路径结果如图6所示,所规划路径的路径形状示意及路径长度对比如表3所示。

表3 路径长度对比结果

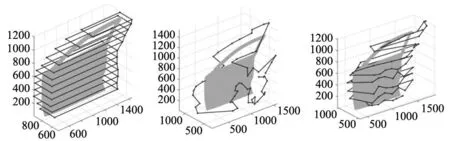
(a) Z型路径结果(b) SOM算法结果(c) 本文算法结果

通过表3中结果,可以看到CGRT所规划的路径长度,较Zigzag算法规划的路径长度缩短54.3%,较贪心算法+SOM算法规划的路径增长42.1%。而3种不同方法所规划路径的测量不确定度指数(即偏离角θ)的最大值、最小值及平均值结果如图7所示。

图7 测量不确定度指数对比

从图7可以看到,通过CGRT算法规划后的测量路径,其所有测点的平均测量偏离角θAve为0.122 rad(约∠7°),较Zigzag型路径减小88.7%,较SOM算法所规划路径减小78.8%。3种路径在仿真测量后,每条路径所测量的全部测点(均为4633个)的偏离角分布占比如表4所示。

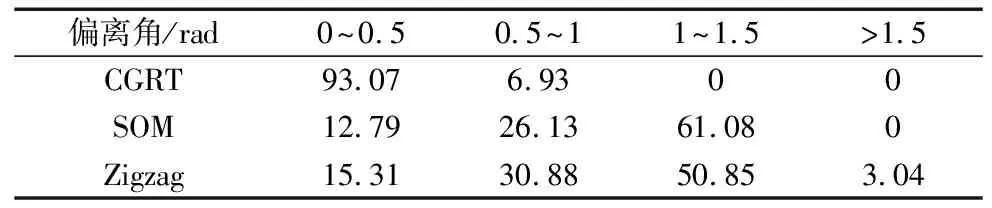
表4 测量偏离角分布表 (%)

通过表4的数据可以反映出,由CGRT所规划的路径,在对其上测点进行测量之后有93.07%的测点的偏离角分布于0～0.5 rad范围内,较SOM算法所规划路径增加80%,较Zigzag型路径增加78%;其余6.93%的测点分布于0.5～1 rad范围内。另外,Zigzag型路径有3.04%的测点测量偏离角大于1.5 rad(约86°),这些测点在测量过程中将无法被线激光传感器有效采集。

4 结束语

针对在线激光连续测量下的全覆盖路径规划问题,本文提出了面向检测精度提升的复杂结构薄板件连续路径规划方法。构建了考虑测量不确定度、路径转角及扫描路径长度等多目标优化模型,并通过线激光检测的局部路径规划以及被测件的生长式全局路径规划等步骤,实现了面向线激光传感器连续测量特点(连续逐行扫描测量、单帧采集数据呈直线分布)的全覆盖路径规划,在整体保证路径总长度合理性前提下,提升了复杂结构薄板件检测精度。本文研究将为汽车车身、航空航天钣金件等复杂零部件的线激光连续测量的路径自动规划提供理论依据。本文所提出的路径规划方法以车门板为仿真规划对象,因而尚不能解决被测件封闭曲面部分的测点遮挡和测量精度问题,在传感器位姿优化与路径规划方法上尚需进一步改进,这也是后续的研究方向。