基于机器视觉的铆接孔圆度误差评定方法*
2024-04-29陈丹丹
郝 博,陈丹丹,杨 斌,韩 焱
(1.东北大学机械工程与自动化学院,沈阳 110819;2.东北大学秦皇岛分校控制工程学院,秦皇岛 066004)
0 引言
飞机的装配过程就是把各种构造形式和功用的结构件按照某种要求加以连接,最后拼装成为一个飞机整机的过程[1]。一架大型飞机上大约有上百万个连接件,连接的方式有很多,主要为铆接或螺栓连接。结构件连接质量直接影响飞机使用寿命。据统计,在飞机机体故障中有75%~80%都是机体机构的连接部位疲劳破坏引起的,而制孔质量是影响疲劳强度的关键因素。提高制孔质量可以降低连接处附加应力、挤压应力,提高连接处的静强度和动强度[2],从而提高连接处疲劳强度,延长飞机的服役时间,保证飞行安全。铆接孔的圆度误差直接反应零件加工质量的好坏,其大小是直接影响几何精度和制孔质量的一项重要指标,影响连接件使用性能和寿命。康仁科等[1]指出为保证飞机飞行安全,需保证足够高的圆度精度要求。卜泳等[2]分析了飞机寿命的关键因素,指出了圆度会影响制孔质量。张宏杰[3]指出圆度等形位误差在我国民用飞机设备的加工和装配中有着非常重要的作用,适当的圆度误差能保证零件加工与装配精度。
目前,圆度误差检测技术在近十年发展较为迅速,已经从传统的手工检测发展到微机自动化检测,从人工接触检测发展到非接触式测量。机器视觉检测相较人工具有精度高、速度快、成本低、操作简单等特点,在多个领域应用广泛。刘庆民等[4]研究了基于机器视觉的非均匀分布点圆度误差评定,证明了该方法的可行性。
本文针对以往圆度误差检测过程存在速度慢、检测成本高等缺陷,采用基于机器视觉的圆度误差评定方法。最后通过实验验证本方法的精确性和可靠性。
1 测量系统设计方案
1.1 系统硬件构成
机器视觉检测系统主要包括相机、光源、VMS4030g移动平台、计算机组成。实验采用长50 cm、宽40 cm、厚1.5 cm的u型钢板模拟飞机结构件。该u型钢板表面均匀分布20个通孔,圆孔半径值R约为42 mm,用来模拟飞机铆接孔。采用VMS4030g移动平台对u型钢板进行定位,通过移动X、Y、Z轴对u型钢板圆孔的图像采集,确保圆孔分布位于采集平台正中心,便于保留图像的完整性。图像采集是紧固孔圆度检测的重要组成部分,是系统的“眼睛”,基于机器视觉的紧固孔圆度误差的在线检测,为保证检测精度和工作效率,系统选用高性能的面阵CCD相机。面阵CCD相机拥有大量感光单元,通过矩阵形式排列,成像速度快、精度较高,具有一次成像的特点[5]。实验光源的选取会直接影响图像质量,对后续特征提取和研究有重要影响。光源可分为自然光源和人造光源。人造光源包括荧光灯、光纤卤素灯、LED光源等。其中,LED光源具有稳定性好、寿命长、光效快、功耗低、绿色环保等优点[6]。针对紧固孔圆度检测的光源选用LED光源。在照明方式上,实验采用高角度LED环形光源进行打光,该照明方式具有光束集中、亮度高及均匀性好等优点[7],适用于本测量系统。系统硬件布局如图1所示。

图1 系统硬件
1.2 检测流程分析
圆度检测过程为:首先,将待测零件放置检测装置,CCD相机进行特征采集,将特征信息导入计算机系统获取待测零件的图像信息;其次,对已识别的图像信息在MATLABA环境中进行图像高斯滤波去噪、图像二值化处理。将灰度化的图像进行拉普拉斯边缘特征提取,获得图像轮廓信息;最后,用最小包容区域法进行边缘轮廓圆度误差评定,判定圆度误差是否满足要求。如果误差在合理范围内,则保留该零件,送入下一个检测环节。反之,则进行人工检测,对零件进行二次判定。检测流程如图2所示。

图2 检测流程图
2 图像采集
由于图像采集过程会受到仪器设备、光照条件、空间分辨率等诸多因素的影响,采集到的图像信息不能达到理想的情况。同时数字图像本身也存在精度低、稳定差等缺陷,使得图像处理过程中灰度值不一致,会产生噪声,从而影响对比度的现象[8]。实验选择在光照充足、安全易操作的环境下进行,调节图像分辨率,获得最佳目标图像,得到20个u型板圆孔图像采集信息,选取圆孔分布位置最佳、包含特征信息最多作为目标圆孔图像,如图3所示。观察并分析图像,调整实验参数,发现在某个强度下噪声数量最多,且强度越远噪声点个数越少,并且此规律服从高斯分布,故需去除图像中的高斯噪声,对实验获得的图像进行高斯滤波处理。

图3 CCD相机采集到的原图像
3 高斯滤波去噪
高斯滤波是一种线性平滑滤波,其去噪过程是首先选择一个卷积模板,分别扫描图像位置每一处像素,获得邻域内像素值的加权平均灰度值,用该灰度值来代替模板中心像素值,从而达到去噪的目的。采集到的圆孔二维图像较为简单,易于分析,其二维高斯函数为:
(1)
在高斯滤波中,卷积核往往会发生变化,其总和不再是一,因此需要对卷积核归一化处理。对卷积核归一化过程为:将邻域坐标值带入二维高斯函数中,获得卷积函数值,用获得的函数值分别进行加权计算,获得坐标点总和为一的坐标值,从而实现归一化处理。图4是选取高斯核为3*3的卷积模板来表示卷积核形成的过程,选择标准差σ=1,其中中心点坐标为(1,1)及其邻域内8个点坐标,如图4所示。高斯滤波去噪的原理就是在采集的图像上方移动高斯核,将图像的像素值高斯核相乘,将输出的结果相加并输出,便可以达到抑制噪声的效果[9]。图7为原图像与高斯滤波去噪后对比图。
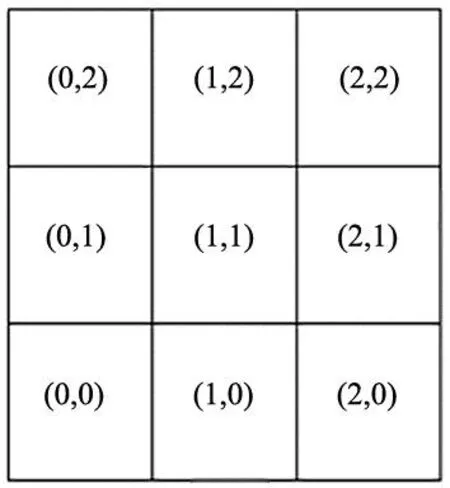
图4 3*3卷积模板
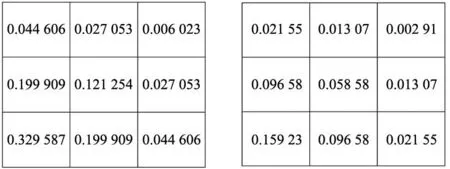
图5 二维高斯函数模板
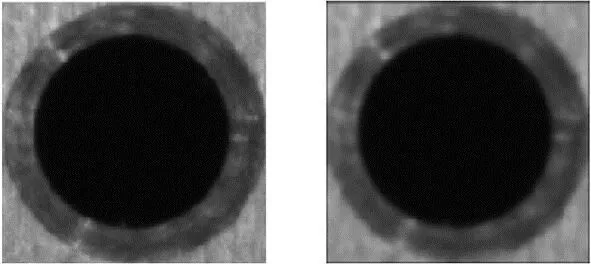
(a) 原图像 (b) 高斯滤波去噪
4 图像二值化处理
为将铆接孔圆度特征与背景信息区分开,需要对所得到的图像进行二值化处理。图像二值化处理是将工件的彩色通道(包括RGB三个通道)转换为单通道输出,从而保证孔圆度特征信息。二值化公式为:
(2)
在MATLAB环境下完成二值化过程。调用rgbzgray函数将彩色图像转换为灰度图像,调用imbinarize函数用于自动求解阈值大小,图8为铆接孔二值化图像。

图8 铆接孔二值化图像
5 图像边缘特征提取
5.1 拉普拉斯图像边缘检测
图像边缘处的像素值往往是不连续的,但是这种不连续可以通过求导来检测。检测常用的一阶求导算子有Sobel算子、Prewitt算子、Roberts算子、Robinson算子等。一阶微分算子方法虽然计算简便、速度快,但是定位不准确,降低识别的准确性。而二阶微分算子是基于一阶导数极值点,对图像求解二阶导数过零点的位置来精确定位图像边缘,测量结果具有更高的准确性。本文采用拉普拉斯算子进行边缘特征求解。
5.2 拉普拉斯边缘检测原理
拉普拉斯算子是通过调整中心像素灰度值与边缘周围像素值的大小关系进行边缘提取。若中心像素灰度比周围像素值高,便会增加中心像素的灰度值,产生“亮者更亮”的效果,反之就降低中心像素灰度值,从而获得边缘特征信息。
拉普拉斯算子基本算法为:
(3)
式中:
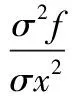
(4)
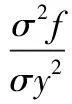
(5)
则
2f(x,y)=f(x+1,y)+f(x-1,y)+
f(x,y+1)+f(x,y-1)-4f(x,y)
(6)
根据拉普拉斯算子可以得到如图9所示的拉普拉斯算子模板。
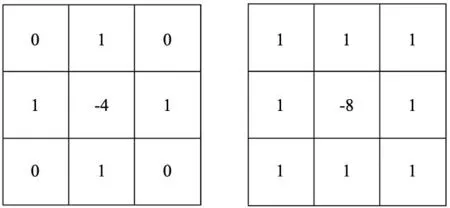
(a) 拉普拉斯运算模板 (b) 拉普拉斯运算扩展模板
由模板可知,当邻域的像素与中心像素相同时,应用邻域模板与原图像进行卷积运算,其结果显示为0;当邻域的平均像素低于中心像素时,采用邻域模板和原图像进行卷积运算,其结果为显示为正数,反之为负数。将卷积结果加在原中心像素上,就可以实现图像的边缘检测[9]。用公式表示为:
(7)
式中:f(x,y)和g(x,y)分别为输入图像与锐化后的图像。由于拉普拉斯算子具有旋转不变性,故不需要考虑原图旋转角度对边缘提取结果产生的影响。图10为边缘检测图像。
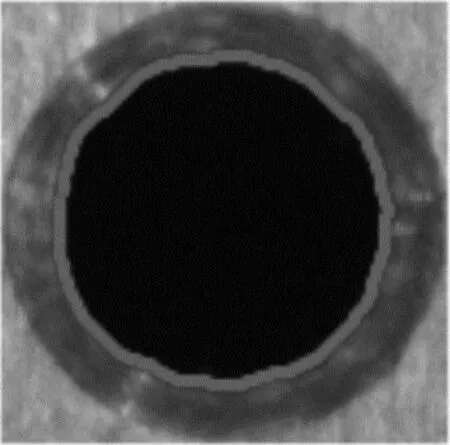
图10 边缘检测图像
6 圆度误差评定
常用的圆度误差评定共有4种:最小二乘法、最小外接圆法、最小包容区域法和最大内切法[10]。本实验测量规则零件圆度误差,使用最小包容区域具有精度较高、速度快、稳定性好,简单易实现的特点[11]。
6.1 最小包容区域法评定误差原理
最小包容区域是指能够刚好将一个给定目标物体恰好包含在内的区域是指理想要素包容被测实际要素时,具有最小半径的包容区域。使用最小包容区域法评定圆度误差,就是按最小条件来确定理想圆与被测实际轮廓的位置[12]。最小条件可以用“2+2”[13-15]形式表示。“2+2”形式的内容为:①先对提取出的轮廓边界随机采集数据点,每4个数据点为一组,共采集10组。已采集的4个数据点称为“控制点”,该控制点满足两个数据点在外圆上分布,剩余两个数据点在内圆上分布的特点。②内圆上两控制点的连线与外圆上两控制点的连线要相交于一点,即4个控制点符合交叉要求。
6.2 实验步骤
步骤1:对已提取的轮廓边缘选取4个“控制点”,(例如:A点和B点,C点和D点)。对于该控制点来说,符合同一方向分布,即沿顺时针分布或者逆时针分布。且选取该控制点的顺序按照内圆、外圆交替进行;
步骤2:将内外圆上的两点分别连接,形成两条直线,分别得到直线L1和L2。求出直线L1和L2垂直平分线斜率K1′和K2′,可表示为:
(8)
(9)
步骤3:分别求直线L1和L2的垂直平分线L1′和L2′,并求出垂直平分线交点坐标O(X,Y),表示为:
(10)
(11)
(12)
步骤4:以O(X,Y)为圆心,以O(X,Y)分别到A(xA,yA)、B(xB,yB)、C(xC,yC)、D(xD,yD)的距离为半径,做一组同心圆;
步骤5:观察图中其他测量点与同心圆之间的位置关系;
若该组同心圆能够全部包含其他测量点,则认为该组同心圆上4个控制点符合最小包容区域法评定圆度误差的条件,则圆度误差为该组同心圆之间的距离。由于最小区域圆圆心至圆上各点距离中,至少各有两个最大值Rmax和最小值Rmin,且两最小值坐标连线与两最大值坐标连线的交点位于最小圆内,则圆度误差可以表示成圆心O(X,Y)到圆上最远点(Xmax,Ymax)的距离与到最近点(Xmin,Ymin)距离之差,圆度误差表示为:
(13)
保留并记录数据;反之,若剩余其他测量点中有任意一点位于该组同心圆包含区域之外,那么认为该组同心圆上4个控制点不符合最小包容区域评定圆度误差条件,故剔除该4个点的组合;
步骤6:按照控制点的选取原则,重新选择控制点并记录数据;
步骤7:重复步骤1~步骤5,直到包含所有符合最小包容区域评定法的组合。
6.3 实验设计
(1)在MATLAB环境下调用BWBOUNDARIES函数获取边缘点坐标,将获得的坐标每隔3.6°取一点实验坐标值,共获取100等份,将100份实验坐标值打乱并随机抽取10份为一组进行圆度拟合,共进行10次实验。例如随机选取一组坐标值分别为(14.012,45.124)、(26.532,24.064)、(33.672,17.935)、(41.347,14.256)、(55.066,13.134)、(60.273,14.732)、(73.225,20.826)、(80.112,27.263)、(50.202,89.635)、(29.673,82.658)将上述实验坐标值进行圆度拟合,获得圆心坐标为(51.11,51.12)。在Python Opencv环境下调用函数获得圆度误差为0.097 mm,半径为42.250 mm。图11为获得的拟合圆和圆心坐标信息。

图11 拟合圆以及圆心坐标信息
(2)将10组数据统计如表1所示。
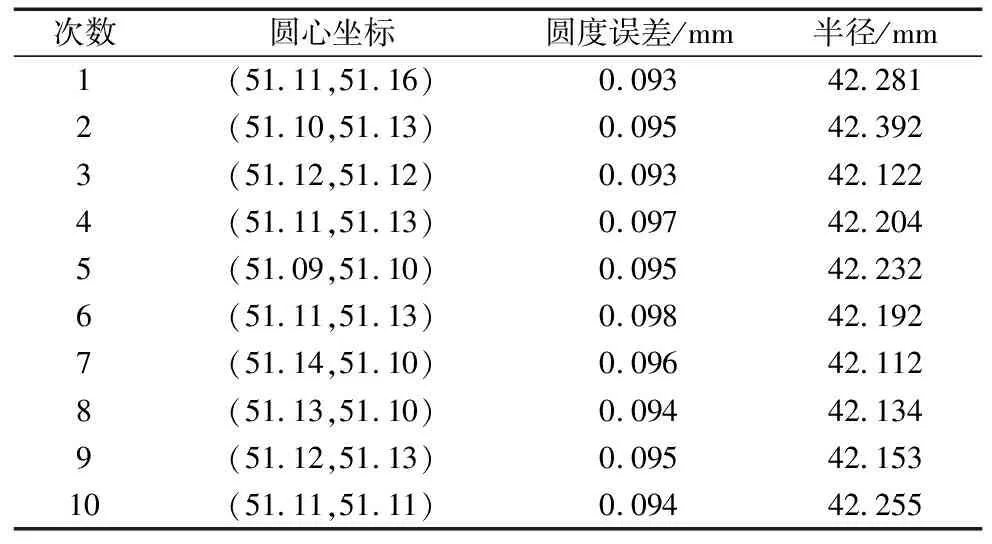
表1 实验数据
根据表1数据可以看出,被测零件圆度误差平均值为0.095,均方误差为0.09,平均半径为42.207 7,可以看出圆度误差分布较为均匀,数据波动性小,也验证了本实验重复性好。以圆度误差f和检测圆半径R的比值表示圆度误差评定的相对误差率,用ε表示:
(14)
实验测得相对误差率为0.002 6,可以间接表示圆度误差的大小,表明圆孔的制造精度。
7 结论
针对工程应用中圆度检测存在的测量精度低、测量成本高等特点,提出了一种基于机器视觉的非接触式圆度误差检测方法。通过CCD相机获取原始图像、对图像进行高斯去噪,通过拉普拉斯算子获得图像边缘信息,最终通过最小包容区域法评估圆度误差信息。通过实验验证该测量系统的有效性。实验硬件设备为CCD相机,软件信息为MATLAB程序平台,测得铆接孔圆度误差平均值为0.095,均方误差为0.09,圆度相对误差率为0.002 6,可见该测量系统成本低、可重复性好、测量精度高。
