平行四杆机构搬运机器人的设计与分析*
2024-04-29郭北涛曲春硕张丽秀
郭北涛,曲春硕,张丽秀
(1.沈阳化工大学机械与动力工程学院,沈阳 110142;2.沈阳建筑大学交通与机械工程学院,沈阳 110168)
0 引言
由于人工成本持续上升和作业效率需求增加,传统的手工物料分拣与搬运方式已无法达到高效自动化操作的标准。因此,在工业化生产中,自动分拣搬运设备的使用逐渐普及。在工业领域,运输设备如搭载多自由度机械臂的AGV机器人、AGV叉车、门式起重机和液压起重机都存在各种局限。
首先,搭载多自由度机械臂的AGV机器人虽然系统柔性较高可以适应各种抓取搬运环境,但其末端抓取力相对较小,同时系统成本较高[1]。然而,AGV叉车虽然能够实现大质量底部抬升[2],但它无法实现顶部夹装与货物姿态的原地旋转调整(进一步压缩操作空间)。这使得运送重物更加耗时且具有挑战性,无法进行快速而精确的调整。其次,门式起重机工作场所固定,不灵活。它们通常安装在特定区域内,并且无法适应多变的环境[3]。这限制了他们在不同应用场景下的使用,降低了效率。液压起重机的液压机构针对中小型货物整体设计过于笨重。同时还易造成液压油泄漏等安全隐患,故障或维修时可能导致系统的运行受阻[4]。
综上所述,本文旨在结合现有技术的各项优点探讨及优化利用平行四杆机构搬运机器人的性能,解决现有抓取力和操作空间等方面的问题,并在提高效率的同时提高系统可靠性。
1 整体结构方案与工作原理
1.1 整体结构方案
根据机器人搬运工作的特点及要求,在研究之初,从机器人对货物的起重抬升、旋转抓取、行进方式及定位导航方案入手,整体结构方案既要满足搬运运输过程中的稳定性、安全性,又要有较高的运行效率,且结构简洁可靠性高。
(1)起重抬升部分。使用步进电机驱动,通过涡轮蜗杆齿轮变速器并辅助弹簧的方式来带动碳纤维平行连杆进行前后摆动,从而实现物品双向抬升与摆放[5]。这样做可以简化轮部控制逻辑和转向调整所需的时间空间,减少对物体惯性状态的干扰,同时提升系统整体效能及运输物品的安全性。
(2)平移与旋转抓取部分。使用编码器减速电机控制螺杆旋转,以带动丝杠上滑块进行前后水平移动。舵机安置在滑块内,将机械爪安装在此舵机下方,实现对货物的水平旋转操作。
(3)行进方式。麦克纳姆轮(简称麦轮),作为一种具有代表性的全向轮,其在全方位移动机器人底盘的应用非常普遍。通过4个独立控制的编码器电机驱动麦轮,配合预设规划路径,利用等百分比操控特性优化[6]对麦轮的PID控制,以实现准确高效的行进方式。
(4)导航定位方案。单纯采用视觉导航定位,单目视觉容易受光照变化、移动物体干扰与遮挡等因素影响。而单纯采用惯性测量单元,因温度、零偏和振动等原因,亦易产生累积误差。采用视觉-惯性导航定位技术,很好的将二者的优势相结合[7]。摄像头通过对固定点位的二维码拍摄实现对惯性测量单元的误差修正,通过单目视觉实现避障和货物识别,同时采用红外测距模块作为在光线不佳时对视觉避障的补充。在保证定位导航精度的同时,减少数据处理量,提高了系统整体效率。
1.2 整体结构图及工作原理
为了满足机器人整体结构设计需要解决的问题,构思设计的整体方案结构,如图1所示。
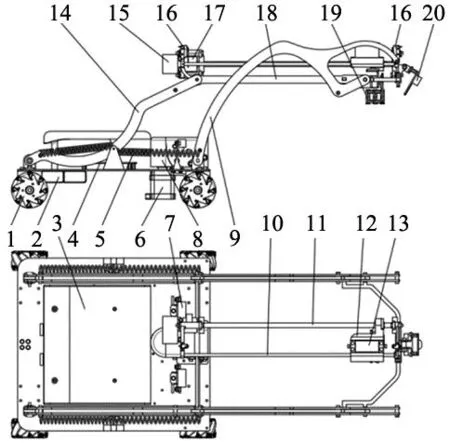
1.麦克纳姆轮 2.电池 3.托盘 4.电路板 5.拉力弹簧 6.步进电机 7.红外测距模块8.蜗轮蜗杆齿轮变速器 9.前端杆 10.滑轨 11.螺杆 12.滑块 13.舵机 14.后端杆15.编码器电机 16.限位开关 17.联轴器 18.水平杆 19.机械爪 20.摄像头
机器人使用4个独立控制的麦轮作为行进机构。步进电机通过蜗轮蜗杆齿轮减速器带动平行连杆实现机器人两侧的抬升、下降。运输过程中,将货物摆放至托盘以实现运输时货物的稳定。通过编码器电机带动螺杆旋转来控制滑块在滑轨上水平移动。控制滑块内的舵机的实现机械爪的水平旋转。顶部的摄像头实现对物体进行识别以及对地面二维码的定位校验与修正,保证集成在电路板内的陀螺仪惯性导航的准确性与安全性。
2 起重相关部件的静力学分析与设计
2.1 静力学模型的建立
由于机器人起重抬升过程近似为匀速过程,为简化模型对机器人起重相关的零件进行静力学分析[8],假设机器人的起重抬升部分主要由平行四连杆A-B-C-D构成且视为刚体,如图2所示。其中A、B铰链固定于机架(车辆底盘),AD与BC杆的长度均为R,与水平面夹角为θ,蜗轮蜗杆齿轮变速器于铰链B对杆施加扭矩T驱动平行四杆机构的运动。G点与A、B两端水平距离均为L0竖直距离为r。前后两对相同规格的拉力弹簧一端固定于机架上的G点,分别另一端与前后摇杆相连于J、E点,二者与水平面的夹角分别为φ1、φ2。杆J点所受弹簧拉力为F1,E点所受弹簧拉力为F2。由于各铰链均采用角接触球轴承进行连接,摩擦系数约为0.002,故可忽略摩擦力对系统的影响。将机构所受货物重力与顶部平移与旋转机构自身重力之和,简化为竖直向下的外力F。
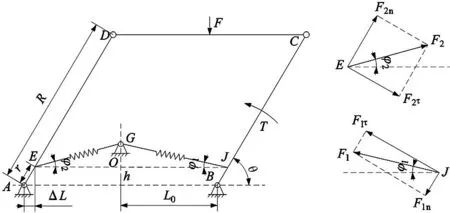
图2 平行连杆机构静力学模型
根据上述模型可得出以下几何关系式,设弹簧初始长度为L0,弹簧GJ的实际长度为LGJ,其弹簧弹性变形量为ΔLGJ,则:
LGO=r-r·sinθ
(1)
(2)
同理,弹簧GE的变形量为ΔLGE,则:
(3)
上述式中φ1、φ2均能通过几何关系求取反三角函数得出,推导过程在此不再赘述。
随着摇杆角度不断发生改变,前后两对拉力弹簧可能会出现3种不同的受力状态,即:
(1)前后两对弹簧都处于受拉状态,此时ΔLGJ+I0>0且ΔLGE+I0>0。弹簧GJ的拉力F1可分解为沿杆分力F1n与垂直于杆的F1τ,则:
F1τ=r·k·(ΔLGJ+I0)sin(θ+φ1)
(4)
同理,弹簧GE所受的拉力F2垂直于杆的分量F2τ为:
F2τ=r·k·(ΔLGE+I0)sin(θ-φ2)
(5)
式中:I0为弹簧预紧长度,mm;k为弹簧刚度,N/mm。
由于两侧杆对称分布,且具有两对相同规格的拉力弹簧(刚度k相同、初始长度相同),不考虑摩擦对扭矩的影响,由于在静力学中,所有力矩的矢量和为0,对轴B列力矩平衡方程得:
T=Tτ-2T1τ+2T2τ
(6)
Tτ=R·Fcosθ
(7)
T1τ=r·F1τ
(8)
T2τ=r·F2τ
(9)
式中:Tτ为F产生的旋转力矩,N·mm;T1τ为F1产生的旋转力矩,N·mm;T2τ为F2产生的旋转力矩,N·mm。
(2)仅弹簧GJ受拉力时,而弹簧GE处于松弛状态不受拉力,此时ΔLGE+I0=0且ΔLGJ+I0>0,杆仅受拉力F1,对轴B列力矩平衡方程得:
T=Tτ-2T1τ
(10)
(3)与之相反,仅弹簧GE受拉力时,而弹簧GJ处于松弛状态不受拉力,此时ΔLGJ+I0=0且ΔLGE+I0>0,杆仅受拉力F2,对轴B列力矩平衡方程得:
T=Tτ+2T2τ
(11)
2.2 弹簧的优化选型
根据2.1节所建立的静力学模型,在平行四杆机构空载或载重工作的过程中,当结构设计参数一定时,即摇杆长度R、弹簧斜拉半径r、机架G点的位置参数一定,驱动摇杆运动所需的扭矩T取决于杆的水平角度θ、弹簧的刚度k、弹簧的预紧长度I0与外力F的大小。本项目目标货物承载能力为10 N,顶部平移与旋转机构自重约为5 N,故F的范围为5~15 N。由于结构参数设计限制,角θ范围为15~155°。由于弹簧长度的限制,弹簧最大预紧长度I0≤50.01 mm。弹簧刚度k选取范围为0~10 N/mm。
采用全局搜索法,使用计算机在上述4个参数(F、θ、I0、k)的范围内根据工程实际搜索最优参数。首先计算在F范围内的任意F(精确到0.1 N)下的,θ在15~155°内的力矩T曲线的极差。在F范围内依次计算极差,找到极差最大值,记录下来此I0、k条件下的极差最大值。在范围内调整I0与k值的大小(根据工程实际情况,I0精确到1 mm,k精确到0.1 N/mm),如图3所示力矩极差最大值分布情况。
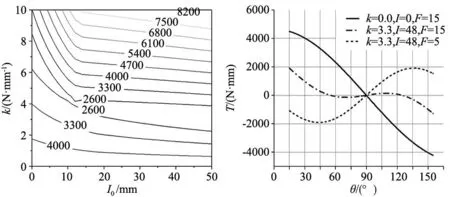
图3 力矩极差最大值分布图
通过计算机在k、I0范围内寻找到力矩极值最大值分布的最小值点为k=3.3 N/mm,I0=48 mm,Tmax=1912 N·mm,即选用此规格的弹簧可以使蜗轮蜗杆齿轮变速器在F在5~15 N的任意力中,输出的最大力矩达到最小。安装此规格弹簧的机构在F=5 N与F=15 N时与未安装弹簧时F=15 N时的扭矩变化情况,如图4所示。
通过图像可以明显的观察到,弹簧安装之后最大输出力矩与力矩变化幅度显著降低。k=0.0 N/mm,I0=48 mm,F=15 N时在∠θ=15°时扭矩最大,Tmax=4 489.45 N·mm。而在k=3.3 N/mm,I0=48 mm,F=15 N时在∠θ=15°时扭矩最大,Tmax=1912 N·mm。最大力矩优化减小幅度达57.4%。由于拉力弹簧具有成熟的工业标准,通过弹簧刚度计算公式进行选择最接近此规格的弹簧即可。弹簧刚度计算公式为:
(12)
式中:k为弹簧刚度,N/m;G为弹簧材料切变模量,304不锈钢:G=7.6×1010Pa;d为弹簧线径,m;d2为弹簧中径,m;n为弹簧有效圈数。
经计算对比,最终确定选择304不锈钢材质,d=2×10-3m,d2=0.01 m,n=46的弹簧,其刚度为3.304×103N/m与上述理论值k=3.3×103N/m十分接近。
2.3 前端杆的设计与有限元分析
通过图4可以发现,在连杆机构采用优化后弹簧连接,依然会在极限条件下产生扭矩绝对值较大的角度位置。由于前端杆为避免货物旋转时与之产生碰撞干涉而设计为弓形,杆在抬升物体时所受应力与变形量亦会随之增加。为了确保机器人结构的强度和刚度,采用Ansys Workbench有限元分析软件进行了静力学特性的仿真模拟,对于验证所选材料的合理性提供了理论支持。
提取图4中扭矩较大的4处受力条件,由2.1节静力学关系式计算得出表1。轴作为固定端,将杆按此表分别进行有限元分析(杆材料为3K200G碳纤维编织预浸布,轴材料为40Cr,网格精度为1 mm)。
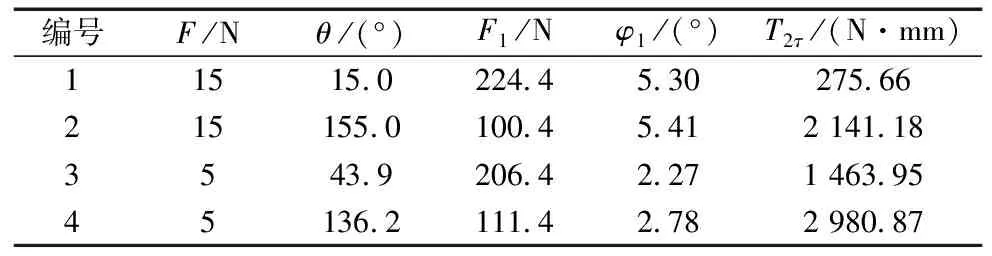
表1 杆的4种受力状态表
4种情况下最大等效应力的最大值出现在编号1,如图5a所示,数值约为10.579 MPa。其远远低于此碳纤维材料的抗拉强度3450 MPa。图5b所示,其最大变形量为0.309 mm,材料满足设计和使用要求。

(a) 等效应力云图 (b) 变形云图
2.4 蜗轮蜗杆齿轮减速器的设计
由图4可知,起重过程中可能会出现力矩方向的反转,故在减速器设计时采用蜗轮蜗杆一方面起到了减速的作用,另一方面涡轮蜗杆其具有自锁的特性可以在力矩反转时防止减速器对电机的反扭,造成破坏[9]。
由于车辆底盘高度的限制,选用机身长度为48 mm的型号为42BYGH47步进电机,其不发生丢步的最大扭矩T0为550 N·mm。与k=3.3 N/mm,I0=48 mm时的Tmax=1912 N·mm,相差3.48倍。
如图6所示,减速器采用三级传动设计,齿轮选用45钢的标准直齿齿轮,模数均为0.8。齿轮1齿数Z1与齿轮3齿数Z3均为32。齿轮2齿数Z2与齿轮4齿数Z4均为16。使用模数为1压力角为20°的渐开线涡轮蜗杆,蜗杆6材料为45钢,头数Z5=4。涡轮5材料为黄铜,齿数Z6=30。
(13)
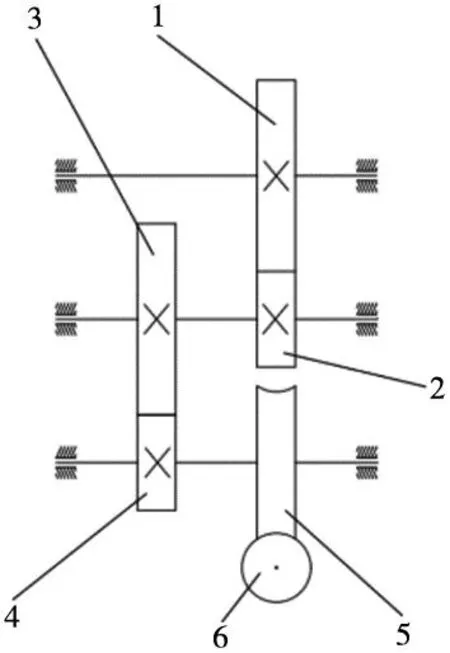
图6 减速器原理图
式中:I为减速器传动比,η为减速器传动效率,η1为齿轮1、2传动效率,η1=97%;η2为齿轮3、4传动效率,η2=97%;η3为蜗轮蜗杆传动效率,η3=95%。
经式(9)计算可得,步进电机的最大扭矩T0经减速器减速后,理论最大输出扭矩T=14 734.5 N·mm,明显大于货物起重所需的最大扭矩Tmax=1912 N·mm。
2.5 机器人工作重心的模拟仿真
通过SolidWorks软件将各材料密度数据输入各零件中装配成型,全车质量为4.8 kg。使用SolidWorks模拟机器人抬升角度∠θ=27°、∠θ=123.5°、∠θ=153°提取摆放尺寸为280 mm×160 mm×150 mm质量约为1.02 kg带有柔性把手的均质箱体。
3种工作状态下机器人车体工作重心改变如图7所示。模拟结果表明其工作重心均在前后两轮的几何内侧,不具有倾覆危险。
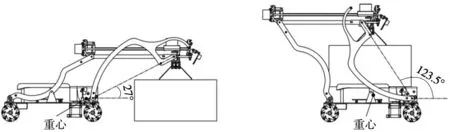
图7 机器人3种状态及工作重心位置示意图
3 其他零部件的选用与分析
3.1 主控模块
为了确保控制系统中各模块能够正常工作,并处理众多的信息流,我们选定基于ATmega2560核心的Arduino Mega单片机作为这款机器人的主控模块[10]。其具备54个数字I/O接口(其中15个可作为PWM输出用途)、16个模拟输入端、4套UART硬件串行口、1个16 MHz晶体振荡器、1个USB连接接口、1个ICSP接口。Arduino Mega单片机,极大程度地满足了对系统各部件软硬件需求。
3.2 螺杆丝杠
作为平移抓取装置的核心部件,螺杆丝杠机构可以通过螺杆与滑块内的铜螺母的相对旋转,实现滑块在滑轨上水平移动[11]。由于螺杆与滑轨水平布置,需承载货物部分重量,且需保证一定水平传动效率,采用304不锈钢、T型、长度为350 mm、螺纹直径为8 mm、导程14 mm的螺杆。螺杆两端使用轴承作为约束。使用JGY370编码器减速电机精准控制滑块移动的距离与速度,可以优化水平启动时的加速度,提高货物平移平稳性。
3.3 舵机及其控制方式
采用TD-8120舵机实现对机械爪的水平旋转。针对传统的舵机控制方法可能会导致过快或突然的转动,这在对机器人的货物抓取上并不理想。采用正弦波的PWM控制可以引入这种平稳且连续的旋转运动[12]。选取正弦周期(0,π),将x的变化范围映射到时间轴上。将sinx的输出映射到旋转角度对应的PWM范围,作为发送到舵机的信号。正弦波形的速度模式还减小了对舵机的冲击,对延长设备寿命同样具备积极意义。
3.4 定位导航避障系统
单目视觉通过采用OpenMV4高清智能摄像头进行图像采集与处理。为保证提取较广视野,摄像头安装在水平杆固定横梁前端。惯性测量单元采用MPU6050电子陀螺仪,通过摄像头对固定位置二维码的识别进行校准[13-14]。红外测距传感器作为视觉避障的互补,采用GP2Y- OAO2YKOF实现对20~150 cm内的光线不佳处的障碍物的规避。
4 实验测试
根据上述设计与分析,制造出实验样机。实验采用了280 mm×160 mm×150 mm质量约为1.02 kg(重量为10 N)的带有柔性塑料把手的箱体作为实验货物。
4.1 基本功能验证
将机器人放置于实验箱体直线距离1 m处(摄像头视线内),如图8a所示。机器人通过摄像头识别箱体摆放角度,计算并调整机器人与箱体底面质心的距离,下降平行连杆机构,并将机械爪旋转至垂直于箱体把手的角度后抓取闭合,如图8b所示。抬升至一定高度后将箱体旋转至与机器人平齐,如图8c所示。继续将箱体调整至运输状态(抬升角度123.5°),如图8d所示。机器人校准对齐二维码以修正惯性导航偏差,如图8e所示。机器人移动至摆放区域,将箱体抬升一段高度后水平移动至后端,于后侧进行下降摆放至规定区域,如图8f所示。

(a) 启动状态 (b) 对齐抓取 (c) 抬升旋转
4.2 极限测试
为准确地揭示机器人在最极端情景下的性能,了解机器人可以安全、有效地执行任务的最大范围和条件,故对机器人起重货物的重量做极限测试。
在机器人自重不变情况下,对箱体质量不断增加,仅进行抬升动作,重复这个过程直至抬升过程步进电机丢步或产生车辆倾覆趋势。实验表明,在货物重量达到2.3 kg时,机器人在抬升货物过程中会达到极限状态,即产生后轮离地现象,但由于减速器的设计冗余并未产生步进电机丢步现象。
5 结论
本研究深入探讨了机器人的机电结构和主要部件设计与控制原理。通过静力学模型分析搬运机器人起重部件的力学特性,作为关键零件并优选弹簧,降低抬升最大输出扭矩。实验结果满足预设性能需求并为优化提供基础。
未来研究可优化杆长或杆的形状,增加设计灵活性。全面分析机器人运动学有助于系统行为理解,改进控制策略,实现精准高效行动。由于对减速器输出扭矩的设计冗余,具有足够空间优化对步进电机的控制[15]。对负载变化应对不足是当前方法潜在问题,通过步进电机控制优化可能明显提高效率、降低能耗。步进电机采用卧式排布方式,将有助于选择更大扭矩的型号以减少齿轮组实现二级传动,提高系统效率以及紧凑性、耐用性和可靠性。
