突发传染病情况下高校行人流建模分析与管理控制：以高校食堂为例

纪鑫　徐嘉明　杨瑷玲　于子兰　唐铁桥

摘要： 为降低密集人群封闭系统在突发传染病情况下的传播风险，以北京航空航天大学沙河校区第一食堂为研究场景，针对存在传染病传播的学校食堂这一特殊场景提出了12种疏散策略。并通过元胞自动机仿真模拟，评估控制策略的效果。仿真结果表明，在疏散前采取出入口消毒、患者隔离等措施，能够降低约40%的整体感染风险。控制措施不仅可以用来解决新冠肺炎背景下“人员聚集场所发现疑似病例的人员疏散”问题，而且在处理一些特定场合的突发情况和指导疫情预防方面也具有应用价值。

关键词： 高校食堂；行人疏散；元胞自动机；疫情防控；管理策略

中图分类号： TB3；U491文献标识码： A

Modeling Analysis and Management Control of Dense Pedestrian Flow in a Closed Area Under the Outbreak of Infectious Diseases： Taking University Canteen as an Example

JI Xina， XU Jiaminga，YANG Ailinga， YU Zilanb， TANG Tieqiaoa

（a. School of Transportation Science and Engineering； b. SHENYUAN Honors College，Beihang University， Beijing 100191， China）

Abstract：In order to reduce the transmission risk of closed systems in densely populated areas during outbreaks of infectious diseases， this study focuses on the first cafeteria of the Shahe Campus of Beihang University as the research scene， and proposes 12 evacuation strategies for school cafeterias where disease transmission occurs. By conducting cellular automaton simulations， the effectiveness of these control strategies is evaluated. The simulation results indicate that implementing measures such as disinfection of entrances and exits， and isolating patients before evacuation can reduce the overall infection risk by approximately 40%. These control measures not only address the issue of evacuating individuals suspected of having COVID-19 in places of congregation， but also have practical value in handling sudden situations in specific scenarios and guiding epidemic prevention efforts.

Keywords： university canteen; pedestrian evacuation; cellular automata; epidemic prevention and control; management strategy

0 引言

21世纪以来，人类面临的主要威胁之一是疫情，如2003年的非典，2009年的甲型H1N1流感和2019新型冠狀肺炎等。高校食堂具有人员多、密度大和流动性强等特征，是疫情防控最重要的公共场所之一。因此，如果在学校食堂中发现病毒携带者，选择合理的人群疏散方案对确保全校师生的安全具有重要意义。本文对高校食堂内的行人流进行建模，模拟不同疏散方案下的情况，从而制定有效的疏散控制策略，为该情景下全部师生的安全有序疏散提供参考方案。

利用元胞自动机进行疏散研究是当前比较流行的研究方法，国内外的学者常常基于研究内容，利用改进的元胞自动机研究不同背景下的人员疏散问题。元胞自动机模型是将行人运动的二维地面区域划分为离散的方格，把行人、建筑物模拟成单元格里的元胞，然后制定行人的运动规则，从而完成模拟过程。其优点在于相对简单，适用于大规模场景的行人行为模拟。杨立中等［1］在已有的元胞自动机交通流模型和行人流模型的基础上，提出了一个模拟火灾中人员逃生的基本模型，用以研究火灾情况下人员的疏散；曹爱春等［2］提出一种多智能体和元胞自动机相融合的大型体育场馆人群疏散模型（Agent-CA），并设计各种人群疏散行为策略作为演化规则，实现个体的差异性以体现个人个性、体力、心理等对疏散行为的影响；杨波等［3］融合元胞自动机与粒子群优化算法，建立了一个新的CA-PSO人员疏散模型，并将其用于模拟教学楼中学生的疏散过程；周美琦等［4］提出了一种基于改进元胞自动机的乘客疏散运动模型，用于研究地铁车厢内发生突发事故时的乘客疏散行为。

目前国内外已有许多有关高校的疏散研究，谢明峰等［5］应用Pyrosim和FDS对某高校教学楼进行建模和火灾数值模拟，并提出了新增合适位置的出口、规划合理的疏散路线等策略；邹馨捷等［6］对高校学生宿舍进行了有针对性的火灾人员疏散安全性分析，研究了对人员疏散安全性影响较大的因素，并提出了消防安全管理措施；都恩源等［7］以高校典型建筑物（如学生宿舍楼和实验室）为研究背景，利用Anylogic仿真软件模拟男女大学生的应急疏散过程，提出了提高逃生效率及避免二次伤害事故发生的策略；汪洋等［8］则以某高校体育馆为研究对象，模拟体育馆内观众满座的情景，并研究观众人数对疏散时间的影响。但这些研究多为火灾或紧急情况下的疏散，并没有将疏散效率与传染病影响因素结合起来。

关于2019-nCoV病毒，国内外学者已经进行了大量相关的研究，李建辉等［9］依据相关研究，率先对2019-nCoV的病毒学特征、传播途径、对环境的抵抗力和消毒方法做了简要描述。在传播因素方面，张丽娟等［10］根据病毒传播特点及城市空间地图模式，建立SEIRQ病毒传播模型，根据元胞自动机原理构建病毒传播机制，并得出结论：初始潜伏者人数、感染力、随机游走、疫苗接种比例等因素在病毒传播时空分布中起重要作用；汪剑眉等［11］基于SIR扩展的非均匀感染力模型，应用吉布斯抽样和机器学习高斯过程回归获得参数估计，模拟差异化场景进行干预敏感度分析，发现降低接触是有效抑制疫情的核心杠杆。桑茂盛等［12］在模型中考虑状态转移参数的饱和特性，建立了一种新传染病模型，并考虑状态转移参数在疫情不同发展阶段的时变特性，从传播规模、传播峰值和传播峰值时间3个维度建立疫情传播风险指标，全面评估疫情传播风险。值得一提的是，喻文等［13］针对高校新冠肺炎疫情传播风险管控做了专门的研究，其结果表明有管控措施和无管控措施相比，能更有效地控制病毒在高校内的传播，进一步证明了在高校内制定合理管控措施的必要性。

本文将在已有研究的基础上，以北京航空航天大学沙河校区食堂为背景，利用元胞自动机模拟疫情下食堂行人流的疏散及病毒扩散，从而得到最优的疏散策略。

1 模型构建

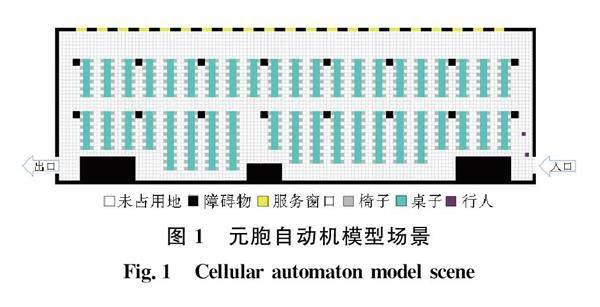
以北京航空航天大学沙河校区第一食堂一楼为蓝本，进行一定的简化：去掉食堂两边无隔离板的用餐区域，仅保留中间的主用餐区域，作为本文疏散策略验证的场景。如图1所示，黑色方块代表障碍物，行人不能通过，必须绕行；黄色方块代表食堂的服务窗口，行人需在此排队打饭；灰色方块代表椅子，在行人打饭（买饮料）结束前不会坐在椅子上，在吃饭时会和椅子重合，代表行人坐在椅子上。青蓝色方块代表桌子，与障碍物类似，行人不能通过，必须绕行。原场景如图2所示。

1.1 基本参数

基本参数λ：行人到达率;pwi：选择窗口i的概率；pci：选择椅子i的概率；pd：选择购买饮料的概率；tci：行人i的吃饭时间；twi：行人i的窗口服务时间；nj：区域j剩余的椅子数量。

本文进行了实地考察，行人进入场景的数据如表1所示。当场景中的人数比较少时，疏散情况也较为简单，因此本文将λ取为高峰时段的行人到达率，根据表2中的观测数据设置为1人/s，服从泊松分布。本文将窗口分为两类：打饭窗口和饮料窗口。本文假设每个打饭窗口具有同质性，即行人选择每一个打饭窗口的概率是相同的。行人选择窗i的概率为1/20。本文假设行人具有同质性，因此每一个行人吃饭时间、排队时间、购买饮料的概率相同。行人i的吃饭时间为900 s，排队时间为30 s，购买饮料的概率为1/10。经观察，行人在打饭后会倾向于选择距离自己打饭的窗口较近的椅子，当自己所打饭窗口周围均没有空椅子时，会优先选择距离其他窗口较近的椅子，最后才会选择距离窗口较远的椅子。因此椅子选择上，本文将整个食堂场景根据椅子与窗口之间的距离进行分区，整个模型共分为四部分（见图3），打饭结束后，处于某区内的行人，会优先选择本区内的椅子，同区内的椅子被选择的概率相同。当本区内的椅子全部被占用后，会优先选择包含窗口的其他区域的空椅子，最后才会选择距离窗口较远的其他区域的空椅子。行人i选择j区域内椅子的概率为1/nj［14］。

具体分区如图3所示，选择区域的优先级为：区域1，选择优先级1→2→3→4；区域2，选择优先级2→1→4→3。

1.2 基本场景

本文使用CA模型来研究行人流，所搭建的场景为简化后的北京航空航天大学沙河校区第一食堂一楼。本文将食堂细分为一个个元胞，每个元胞只有两种状态：一种是空闲，另一种是被行人、桌子、椅子、墙壁、服务窗口等占用。给出基本假设［15］：

1）每个元胞大小为0.4 m×0.4 m，每个行人占据一个元胞。由于疫情防控需要，本文将场景里的长椅根据其长度拆解成若干个有间隔的小椅子（包括6个元胞、8个元胞和9个元胞3种），且每个椅子的大小为0.4 m×0.4 m。服务窗口的大小为0.4 m×1.2 m，为横向连续的3个元胞。

2）假设场景里的行人具有同质性，其速度均为1 m/s。

1.3 演化规则

模型考虑正常运行和紧急疏散两种情况，分别对应两套演化规则。

根据行人的运动特点，本文采用冯·诺依曼邻域的元胞自动机模型［16］来模拟行人在食堂中的运动。在冯·诺伊曼邻域的元胞自动机模型中，行人每次移动时会选择上下左右4个邻元中的空闲元胞中距离目的地最近的元胞并向其移动，如果存在多个距离目的地最近的元胞，则以相同的概率随机选择其中一个，只有在邻元没有空闲或行人处于排队状态时才会停在原地。正常运行情况下，行人进入食堂，然后选择自己心仪的窗口，走向窗口排队等候打饭。打饭成功后，在pd的概率下，行人有可能选择购买饮料。若行人选择购买饮料则会优先走到饮料窗口，排队等候购买饮料，饮料窗口为场景中最右侧的服务窗口，购买成功后选择座椅，走向座椅，然后坐下吃饭；若行人不购买饮料，则直接走向选择的座椅。用餐完毕后，行人将按照当前自己所在位置的最小路径走向出口离开食堂。

緊急情况下，当管理者发布“场景中包含传染病患者”的信号后，场景中一切服务停止，全部行人停止移动，行人等候管理者发布指令，根据所发布的指令再进行相应的疏散策略。

本文将患者设为第npatient个进入模型，在运行一段时间后，管理者会接到相关通知，开始紧急疏散，根据本文预先提供的疏散策略进行疏散。基本运行规则如图4所示。

2 疏散策略

本文提出了12种疏散策略。每种策略由疏散开始前对食堂出入口采取的措施和对患者采取的措施，以及疏散开始后场景中行人的运动方式3个部分组成。

1）开始前对食堂出入口的措施分为两类：A1 对出入口附近一定半径的扇形区域进行消毒处理，并认为该区域不再存在病毒；A2 不对出入口采取消毒措施。

2）开始前对患者的措施分为两类：B1 采取隔离措施，即对患者采取戴口罩等措施，使病毒在此之后不再由患者向外传播；B2 不采取隔离措施，即病毒会持续由患者向外传播。

3）开始后场景中行人的运动方式分为3类：C1 直接疏散，不采取其他干预措施；C2 患者病毒传播范围外的人先疏散，其他人等待这部分人全部离开场景后再疏散；C3 患者在其他人全部离开前保持不动，其他人尽可能绕过患者经过的路线（含有病毒的区域）。

将各部分策略分别组合，一共可以得到C12·C12·C13=12种不同的疏散策略。各疏散策略对应如表2所示。

病毒的存活受温度、相对湿度、附着物等条件的影响，这使得在研究中难以将病毒的有效传播时间、扩散能力等定量处理。因此，为了更普适地寻找一种最佳的疏散策略，使用行人经过含有病毒的元胞（下简称病毒元胞）的计数次数作为行人的感染风险，记为R。如图5所示，将粉色的元胞视作病毒所在的元胞，行人按照图中箭头所指示的路线行走，在连续的时间步中依次经过病毒所在的元胞1、元胞2和元胞3，总计经过3个病毒元胞，所以记录该行人的感染风险R=3（假设行人不再经过其他含有病毒的元胞）。

当行人行走路线间断地经过了多个病毒元胞时，将所有的病毒元胞的计数次数累加求和。如图6所示，将粉色的元胞视作病毒元胞，行人按照图中箭头所指示的路线行走，先在连续的时间步中依次经过病毒所在的元胞1和元胞2，记录感染风险为R1=2，然后经过元胞9和元胞10，记录感染风险为R2=2。那么该行人的感染风险R=∑2i=1Ri=R1+R2=2+2=4。

对于病毒元胞，本文做出假设：1）患者病毒传播范围内的元胞会变为病毒元胞；2）当元胞变为病毒元胞后，始终保持该状态；3）病毒元胞不具有扩散到其他元胞的能力；4）采取消毒措施后，病毒元胞变为无病毒的普通元胞。

按照在模型構建中所搭建的初始场景，设定参数如表3所示。

本文设定患者到达窗口前疏散开始。为了减少随机性对疏散初始场景的影响，经过空场景输入行人进行多次仿真后，选取了场景中行人分布较为普遍的一种疏散初始场景，如图7所示。

以该场景为疏散的起始场景，分别运用12种疏散策略进行仿真实验，对每种疏散策略各进行5次重复实验。取个体指标maxLi和群体指标Li-，αi作为结果的评价指标，对重复实验数据取均值，得到结果如表4所示（不考虑患者的Li-）。

表4中，maxLi表示非患者的其他所有行人中感染风险的最高值；Li-表示非患者的其他所有行人中感染风险的平均值；αi表示非患者的其他所有行人中感染风险为0（即可视为未被感染）的行人占总行人的比例。下面将分别从疏散策略的3个组成部分对数据结果进行分析。

2.1 疏散开始前对食堂出入口的措施

从图8～图10和表5～表7可以看出，其他两部分策略相同的条件下，对食堂出入口采取措施A1比采取措施A2时行人感染风险的最大值max Li平均减小约8%、平均值Li-平均减小约44%；提高αi方面，平均提高约40%。即疏散开始前对食堂出入口附近区域内进行消毒处理在降低最大感染风险方面并不明显，但是能够明显降低整体行人的感染风险平均值，并且提高无感染风险的人数比例。

2.2 疏散开始前对患者的措施

从图11～图13和表8～表10可以看出，其他两部分策略相同的条件下，对患者采取措施B1比采取措施B2时行人感染风险的最大值maxLi平均减小约20%、平均值Li-平均减小约38%；提高αi方面，平均提高约15%。即疏散开始时及时对患者采取一定的隔离措施如戴口罩等，可以有效降低场景中行人易感染风险的平均值，对降低最大感染风险和提高无感染风险人群的比例也有一定的效果。（表中“–”表示数值小1%）。

2.3 疏散开始后行人的运动方式

从图14～图16和表11～表13可以看出，其他两部分策略相同的条件下，行人运动的方式C2，C3相比于C1在行人感染风险的最大值max Li平均降低4%、提高5%；平均值Li-变化程度小于1%。而提高αi方面，运动方式C2，C3相比于C1平均提高约5%、9%，但是运动方式C2提升的效果并不稳定。即疏散开始后采取“先让患者周围一定范围外的人疏散，其他人再疏散”这一策略能够降低最大感染风险，并且提高无感染风险人群的比例；采取行人绕行病毒区域这一运动方式能够较明显提高无感染风险人群的比例。行人的运动方式对降低行人易感染风险平均值的效果浮动大且不稳定。

3 结论

本文针对存在传染病传播的学校食堂这一特殊场景提出了12种疏散策略，通过仿真实验分别模拟了不同策略的运动状态，并通过定义“易感染等级”等变量来比较、评价不同策略的优劣。仿真结果表明，在传染病已经在场景中扩散的情况下，首先消灭传染源所释放的病毒或阻断传染源（患者）的传播对减少场景中被感染的人数起到积极的作用。其次，在对人群进行疏散时，要尽量避免行人与传染源持续近距离接触，尽量远离传染源及其经过的路径疏散。在条件允许的情况下最好在疏散开始时对出入口等必须经过的区域进行病毒处理。本文建立的元胞自动机模型以北京航空航天大学沙河校区第一食堂一楼为蓝本，行人运动过程中的各项参数均来源于实地调查，可以代表大部分高校的实际情况，只需要通过修改场景大小以及场景中的元素就可以变换为其他不同的场景（如将场景尺寸缩小，调整桌椅的朝向，将服务窗口改变成讲台和黑板就可以将场景变为教室），疏散策略也能在各种场景中实现，具有代表性。

本研究也存在着不足。仿真实验对行人的输入采取的是泊松分布输入，这与现实场景存在着一定的差别。在行人更加密集的封闭场所中，行人的数量和运动差异性会进一步增强，这可能会使行人在场景中产生拥挤导致难以避开有病毒留存的区域，提高被感染的风险。在行人运动方面采取的元胞自动机模型，较难再现行人运动的多方向随机性，并且较难体现疏散时的慌张等心理状态对行走速度的影响。

参考文献：

［1］郑海兵.行人交通流研究综述［J］.山东交通科技， 2018 （4）： 27－29，40.

ZHENG H B. A review of pedestrian traffic flow research ［J］. Shandong Traffic Science and Technology， 2018 （4）： 27－29，40.

［2］杨立中，方伟峰，黄锐，等.基于元胞自动机的火灾中人员逃生的模型［J］.科学通报，2002，4（12）：896－901.

YANG L Z， FANG W F， HUANG R， et al. A model for human escape in fire based on metacellular automata［J］. Science Bulletin，2002，4（12）：896－901.

［3］曹爱春，杨晓艇，侯旭东.Agent-CA的体育场馆人群疏散模型［J］.计算机工程与应用，2013，49（24）：229－232.

CAO A C， YANG X T， HOU X D. Agent-CA crowd evacuation model for stadiums ［J］. Computer Engineering and Applications，2013，49（24）：229－232.

［4］杨波，陈丹丹，夏颖，等.基于GIS的CA-PSO多出口场景疏散模型研究［J］.中南民族大学学报（自然科学版），2017，36（1）：107－112.

YANG B，CHEN D D，XIA Y，et al. Research on CA-PSO multi-exit scenario evacuation model based on GIS［J］. Journal of Central South University for Nationalities （Natural Science Edition），2017，36（1）：107－112.

［5］周美琦，杨晓霞，张纪会，等.基于改进元胞自动机模型的地铁车厢乘客疏散模拟［J］.复杂系统与复杂性科学，2021，18（3）：35－44.

ZHOU M Q， YANG X X， ZHANG J H， et al. Simulation of passenger evacuation in subway cars based on improved metacellular automata model［J］. Complex Systems and Complexity Science，2021，18（3）：35－44.

［6］谢明峰，鲁义.高校教学楼火灾与人员疏散模拟研究［J］.消防科学与技术，2021，40（1）：85－90.

XIE M F， LU Y. Simulation study of fire and personnel evacuation in a college building［J］. Fire Science and Technology，2021，40（1）：85－90.

［7］都恩源，陈心如，韩祥临，等.高校典型建筑物学生群体应急疏散研究［J］.湖州师范学院学报，2021，43（4）：81－88.

DU E Y， CHEN X R， HAN X L， et al. Research on emergency evacuation of student groups in typical buildings in colleges and universities ［J］. Journal of Huzhou Normal College，2021，43（4）：81－88.

［8］汪洋，朱国庆，周金炬，等.高校体育馆人员疏散模拟研究［J］.消防科学与技术，2020，39（9）：1215－1218.

WANG Y， ZHU G Q， ZHOU J J，et al. Simulation study of personnel evacuation in college gymnasium ［J］. Fire Science and Technology，2020，39（9）：1215－1218.

［9］李建辉，麻婧，康文，等.新型冠状病毒2019－nCoV的病毒学特征、传播途径及抵抗力［J］.临床医学研究与实践，2020，5（S1）：3－5.

LI J H， MA J， KANG W， et al. Virological characteristics， transmission route and resistance of novel coronavirus 2019-nCoV［J］. Clinical Medicine Research and Practice，2020，5（S1）：3－5.

［10］ 汪劍眉，李钢.新冠肺炎非均匀感染力传播模型与干预分析［J］.电子科技大学学报，2020，49（3）：392－398.

WANG J M，LI G. Analysis of non-uniform infectious power transmission model and intervention for new crown pneumonia［J］. Journal of the University of Electronic Science and Technology，2020，49（3）：392－398.

［11］ 桑茂盛，丁一，包铭磊，等.基于新冠病毒特征及防控措施的传播动力学模型［J］.系统工程理论与实践，2021，41（1）：124－133.

SANG M S， DING Y， BAO M L， et al. A propagation dynamics model based on the characteristics of new coronavirus and prevention and control measures［J］. Systems Engineering Theory and Practice，2021，41（1）：124－133.

［12］ 喻文，邵畅志，王侃，等.基于SEIR模型的高校新冠肺炎疫情传播风险管控研究［J］.武汉理工大学学报（信息与管理工程版），2020，42（4）：368－372.

YU W， SHAO C Z， WANG K， et al. Study on the risk control of new crown pneumonia epidemic transmission in universities based on SEIR model［J］. Journal of Wuhan University of Technology （Information and Management Engineering Edition），2020，42（4）：368－372.

［13］ TANG T Q， ZHANG B T， XIE C Z. Modeling and simulation of pedestrian flow in university canteen［J］. Simulation Modelling Practice and Theory， 2019， 95： 96－111.

［14］ VANDOREMALEN N， BUSHMAKER T， MORRIS D H， et al. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1［J］. The New England Journal of Medicine， 2020， 382（16）： 1564－1567.

［15］ CASANOVA L M， JEON S，RUTALA W A， et al. Effects of air temperature and relative humidity on coronavirus survival on surfaces［J］. Applied and Environmental Microbiology， 2010， 76（9）： 2712－2717.

［16］ CHIN A W H， CHU J T S，PERERA M R A， et al. Stability of SARS-CoV-2 in different environmental conditions［J］. The Lancet Microbe， 2020， 1（1）： e10.

（責任编辑 李 进）

收稿日期： 2022－03－18；修回日期： 2022－04－26

基金项目： 国家自然科学基金（72171006，71771005）

第一作者： 纪鑫（2000－），男，内蒙古呼伦贝尔人，硕士研究生，主要研究方向为行人流建模分析。

通信作者： 唐铁桥（1977－），男，湖南邵阳人，博士，教授，主要研究方向为行人流建模分析。