基于含时网络数据的卫星网络模体识别方法研究
2024-04-29胡博仁裴忠民罗章凯丁杰
胡博仁 裴忠民 罗章凯 丁杰
摘要: 鉴于开展卫星网络局部结构研究是理解网络性质的重要手段,考虑星间链路天线可见性约束等条件,提出了一种基于含时网络数据的卫星网络模体识别方法,建立了从TLE文件输入到子结构识别输出的模体识别流程。以GPS卫星网络的三节点三边模体识别为例,结果发现在短时段内卫星天线最大扫描范围与具有特殊结构意义的三角形M4子图浓度呈正相关。
关键词: 卫星网络;模体识别;子图浓度
中图分类号: TP393;TP399 文献标识码: A
On Motif Counts Method of Satellite Network Based on Temporal Network Data
HU Borena, PEI Zhongmina,LUO Zhangkaia,DING Jieb
(a. Science and Technology on Complex Electronic System Simulation Laboratory;b. Department of Electronics and Optical Engineering, Space Engineering University, Beijing 101416,China)
Abstract:Conducting research on the local structure of satellite networks is an important means to understand the nature of networks. Considering the visibility constraints of inter-satellite link antennas, a satellite network motif counts method based on temporal network data is proposed, and a motif counts process is established from TLE file input to substructure identification output; taking the three-node three-edge motif counts of GPS satellite network as an example, we found that in a short period of time maximum scanning range of the satellite antenna was positively correlated with the concentration of the triangular M4 subgraph with special structural significance.
Keywords: satellite network; motif counts; subgraph concentration
0 引言
近年来,随着信息技术和航天技术的不断发展,在轨卫星数目的增加造成了卫星网络节点密集化及网络结构复杂度的提高。从空间资源高效利用和确保网络安全运行的角度出发,开展卫星网络结构特性分析具有重要意义。复杂网络作为网络科学的重要分支,通过研究结构特性和组织方式来探索和理解复杂系统的结构、行为和功能,为卫星网络研究提供了有力的方法支持。广大学者通过复杂网络的相关理论对卫星网络进行了深入的研究。武健等[1]基于复杂网络理论和灰色关联度分析方法,提出了网络微观层面的卫星节点重要度评估指标。朱林等[2]综合节点介数、节点紧密度和节点距离对卫星网络节点重要性的贡献,提出了稳态卫星网络节点重要性评估方法。王莹[3]提出了衡量卫星通信网络整体结构性能的卫星移动通信网约束连通度指标,重点在于度量节点间满足约束条件的可用路径。林琪等[4]基于卫星网络拓扑特征,包括度分布、平均最短路径和网络直径等,提出了卫星网络综合效能评估方法。
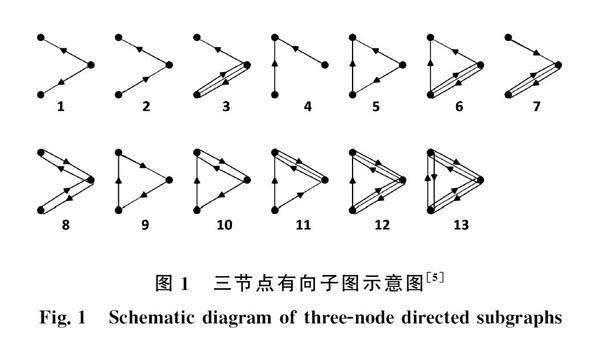
目前,运用复杂网络理论对卫星网络进行结构分析和研究时,多从网络的整体结构特性出发,如网络连通度、度分布等,或注重节点或边的属性,如节点重要性评估,鲜有卫星网络局部结构相关的研究。然而局部结构作为网络结构分析的中尺度视角,与卫星网络结构的微观、宏观分析角度同样重要,有时局部结构特征能更好地揭示网络结构与功能的内在关系。模体概念最早于2002年由Milo等[5]提出,定义为网络中重复出现的局部子图结构。如静态三节点有向图共有图1中13种,其中某一种子图在网络中多次出现,且满足{P,U,D,N}[5]条件,即可称之为模体。
Martí Rosas-Casals等[6]对欧洲电网的结构稳定性进行研究,发现相对于分散的去中心化连接模式,四节点三边规模的星型模体数量增加会加剧网络的脆弱性。Paul Schultz等[7]提出是否存在某种网络模体能提高电网结构稳定性的问题,发现弯路模体(Detours motifs)在提高网络稳定性上具有重要作用,三角形模体即为最简单的弯路模体(见图2)。孙晓伟[8]以引文网络、合作网络和作者引用网络的三阶网络模体为研究对象,挖掘论文和作者间引用、合作关系的演化规律。
相比电力网络和论文引文网络等静止网络,卫星网络具有动态高时变、网络数据获取难等特点,进行卫星网络局部子图结构研究具有一定的难度。本文旨在为卫星网络结构分析中引入中尺度的模体角度,提出一种基于含时网络数据的卫星网络模体识别方法,解决卫星网络模型建立、网络数据构建和动态模体识别过程中条件不清晰、数据量大等问题。该研究对于揭示卫星网络局部结构与整體性质之间的关系有着一定的意义,为卫星网络局部结构研究提供了方法借鉴和技术参考。
1 基于含时网络数据的卫星网络模体识别方法
识别卫星网络中频繁出现的局部高阶子结构,需考虑网络的动态时变性并自行构建卫星网络数据。针对上述问题,本文提出了一种基于含时网络数据的卫星网络模体识别方法,流程如图3所示。借助STK和Matlab等软件,建立仿真卫星网络模型,设置网络节点之间的连接条件;生成包含时间属性的卫星网络数据;使用动态模体识别算法进行子图计数并计算子图浓度等指标,以此来进行卫星网络结构分析。
1.1 建立卫星网络模型
本文研究的卫星网络,以卫星星座为主体,泛指由存在于近地空间的卫星节点和地面段的地面站节点组成,节点之间以星间链路和星地链路两种形式建立连接,用于信息传输和星座业务实现的网络系统,如图4所示。
下载Celestrak网站的卫星星历(TLE)文件,导入STK,建立近地空间的卫星星座模型,或者根据轨道六参数,确定卫星的轨道和位置。卫星网络中的地面站节点设置与具体卫星系统类型有关,如卫星导航系统的地面段包括主控站、注入站和监测站。查阅资料得到站点的经度、纬度信息,建立地面站点,或查询STK自带地面站库,直接添加。
卫星网络中的边包括星地链路和星间链路,根据卫星网络实际运行情况,结合简化假设,设置模型中边的连接准则。星间链路的建立条件包括[9]:几何可视条件、天线可视条件和传输距离条件。星间链路天线可见性的约束条件[9]:
1.2 构建卫星网络数据
含时网络[1011]在复杂网络模型的基础上,加入了时间维度,用(V,E,t)表示,其中t代表网络连边的发生时刻,主要用来刻画离散时间内网络连边断续存在的情形。比如在卫星网络进行数据传输时,A和B之间的连边仅在进行数据传输时存在,数据传输结束后,连边也随之消失。只在A、B之间建立一条连边已无法描述节点相互作用时刻变化的特点。
网络的动态变化具体表现为边数量的增减或节点数量的增减,而卫星网络的节点数量通常不发生变化,边的数量随时间不断变化。用三元组(u,v,t)表示卫星网络中的连边,u表示边起点,v表示边终点,t表示u和v在t时刻处于连接状态。
Matlab与STK互联之后,可以调取卫星节点和地面站节点的相关数据,包括某时刻下,卫星之间的距离和卫星的高程,卫星与地面站是否满足几何可见性约束等。依据卫星网络模型中边的连接准则并进行条件判断之后,获取某一时间段内的网络三元组边数据,完成卫星网络数据的构建。
1.3 识别卫星网络模体
网络模体识别是网络模体研究的重点和难点之一。经典的模体识别算法[12]主要是面向静态网络,生成若干个与实证网络节点数和节点的度序列相同的随机网络;在实证网络和随机网络中搜索某一规模的子图,将同构的子图归为一类;比较每一类子图在实证网络和随机网络中的出现次数以确定其统计意义,从而确定是否为网络模体。常用的静态网络模体识别工具包括MFinder[13],FANMOD[14],MODA[15]和NemoMap[16]等。
卫星网络是具有时变性的动态网络。面向动态网络的模体识别算法包括基于流模型的StreaM[17]和Massive Streaming Data Analytics[18],SNAP(Stanford Network Analysis Project)框架下的Motifs in temporal networks 动态模体识别抽样算法[19]和oDEN算法[20]等。
构建卫星网络数据后,选用SNAP框架下面向大规模网络数据的抽样动态三节点模体识别算法,该算法适用于二节点三边和三节点三边的36种有向子图计数,如图6所示。由于网络带有时间属性,引入时间参数δ,并定义δ卫星网络模体:由具有时间属性的边组成的子图,模体中的有向时空边(带时间戳)具有先后顺序,受时间段δ约束,即连接关系均发生在时间段δ内,用数学表达式可表示为
其中,t1,t2,…为卫星网络模体中的边连接时刻。
本文建立的卫星网络模型,卫星间连接和卫星与地面的连接均为无向边,三节点三边无向图共4种(见图7),需将算法识别的有向子图转换为无向子图。
对无向卫星网络数据进行模体识别时,有向图中有带环的子图如M1,2,会出现重复计数的现象,使得计数结果多于实际无向图,故不考虑。 SNAP框架下的temporal motifs 算法为提高识别速度运用了抽样思想,使对应同一种无向子图的有向子图计数结果存在细微差别,故取有向图计数结果的均值为无向图计数结果,具体计算见公式(4):
4种三节点三邊无向图中,M1、M2、M3均为星型子图,指单节点为中心节点,其他节点直接与中心节点相连构成的子图,M4为三角形弯路子图,有利于网络结构的稳定,重点关注子图M4的出现次数和子图浓度。子图浓度是指相同实验条件下,同等子图规模的某种子图所占的比例,体现了网络中同等规模不同连接模式子图的分布情况,计算如式(5)所示。
其中,Ck为某子图规模下第k个子图结构的子图浓度,Mk为第k个子图的出现次数,该子图规模下,共有N个异构子图结构。
2 实例分析
以GPS为例,建立由空间在轨卫星和地面监测站组成的卫星网络模型。GPS由空间段、地面段和用户终端组成,本文不考虑用户终端。空间段由30颗中轨道卫星组成。地面段包括主控站、监测站及注入站,主控站[21]主要是收集和处理监测站的观测数据;监测站利用复杂的GPS接收机跟踪从监测站上空经过的GPS卫星,收集导航信号、范围测量数据和大气数据等;注入站在卫星离开其作用范围之前进行指令等信息注入。综上,为简化模型,故本文只考虑GPS卫星与监测站之间的信息传输,建立由空间段卫星节点和监测站节点组成的卫星网络,且不考虑地面节点间的连接。在STK软件中建立的16个GPS监测站点如图8所示。
使用Celestrak网站的两行根数(TLE)文件,构建GPS空间段。TLE文件的时间为2021年12月21日,导入STK软件,卫星节点数量为30,地面站节点和卫星节点数目总和为46,3D示意如图9所示。
设定节点间的连边条件。某时刻下,若卫星间的距离lAB 满足星间链路的几何可见性约束及天线可见性约束,则认为卫星节点间建立了双向连接,不考虑传输距离等因素的影响;某时刻下,若地面站节点与卫星节点满足可见性约束,则认为建立了从卫星到地面站的双向连接,不考虑时延和误码等因素。在星间链路建立时,天线可见性约束(见式(1))中的卫星天线最大扫描范围αmax起关键作用,对网络拓扑结构具有较大影响[22]。结合实际卫星网络运行情况并考虑数据量规模等问题,设置实验时长为86 400 s,时间步长为1 s,天线最大扫描范围分别为30°,45°和60°,三种情况下的GPS卫星网络边数据,均以txt文件格式输出,每一行皆为三元组(u,v,t),代表一条边,输出数据的情况如表1所示。
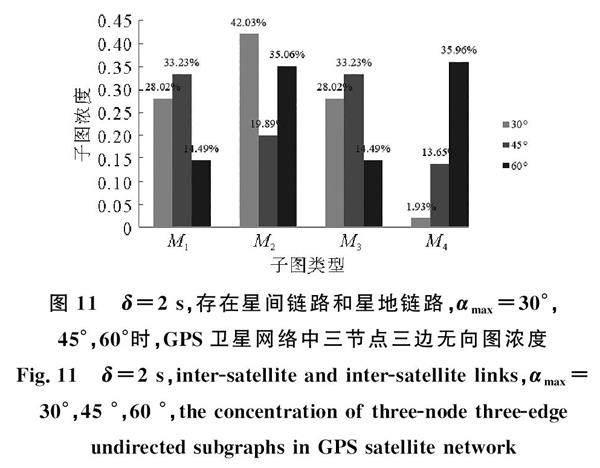
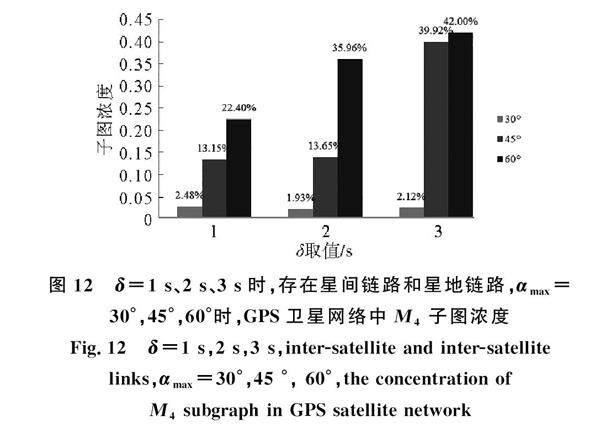
若忽视卫星与地面站之间的连接(简称为第1种情况),GPS卫星网络将是一个独立自主运行的系统。考虑卫星网络信息传输的时效性,时间参数δ取值为1s、2s、3s(三边连接时间点的最大间隔不超过δs),三节点三边无向图子图浓度统计结果如图10、图11和图12所示,子图浓度计算式如式(5)所示。
既考慮星间链路,又考虑星地链路(简称为第2种情况)时的结果如图11、图12所示。
由图10、图11和图12可得:1)图10、图11和图12所处情况下,天线最大扫描范围都与M4子图浓度呈正相关,αmax越大,卫星节点间的连接越多,全连通结构子图的出现概率越大,M4子图浓度越高,越有利于网络的稳定。 2)αmax=30°和60°时,第2种情况的M4子图浓度均高于第1种情况,说明在αmax值较小时,可以借助星地链路建立 “卫星-地面站-卫星”的三节点全连通结构;在αmax值较大时,卫星节点之间的联系紧密,第1种情况下的网络具有较高的连通度,增加星地链路之后,地面站同时与多个卫星建立连接,增加了三节点全连通结构的出现次数,提高了M4子图浓度。3)按照三条边的发生顺序,M1和M2的边路径发生了一次转换,而M3发生了两次转换,发现在第1种情况和第2种情况的不同αmax下,M1和M2总是具有相同的子图浓度。在本文的卫星网络模型中,受节点连接关系特性的影响,节点之间的连接在某一时间段内持续存在,使得边路径发生一次转换的M1和M2同时出现并具有相同的出现次数。
3 结语
建立卫星网络模型、构建卫星网络数据和识别卫星网络模体,提出了卫星网络模体识别的一般方法,建立了从TLE文件输入到子结构识别输出的卫星网络模体识别流程;以GPS卫星网络的三节点模体识别为例进行了实证分析,结果表明:此方法基本可以实现卫星网络三节点无向图模体识别,子图浓度分布受模型相关参数值的影响较大,短时段内天线最大扫描范围与M4子图浓度呈正相关。
本文提出的卫星网络模体识别方法,包括如下不足:建立的卫星网络模型较为简单,特别是网络在建立星间链路和星地链路时,考虑的相关约束和条件较少,假设较多;受动态网络模体识别算法的影响,仅能识别三节点模体。下一步可以分析网络遭受攻击和损害情况下M4子图浓度的变化情况,进行卫星网络节点重要性评估和鲁棒性评估等。
参考文献:
[1]武健,刘新学,舒健生,等. 基于复杂网络的卫星重要度评估[J]. 火力与指挥控制, 2014, 39(5): 60-63.
WU J, LIU X X, SHU J S, et al. Satellite significance assessment based on complex network[J]. Fire Power and Command Control, 2014, 39(5): 60-63.
[2]朱林,方胜良,胡卿,等.卫星时变拓扑网络节点重要度评估方法[J].系统工程与电子技术,2017,39(6):1274-1279.
ZHU L, FANG S L, HU Q, et al. Evaluation method of node significance of satellite time-varying topology network[J]. System Engineering and ElectronicTechnology,2017,39(6):1274-1279.
[3]王莹.卫星移动通信网若干理论和技术研究[D].武汉:华中科技大学,2008.
WANG Y.Research on theoretical and technical of satellite mobile communication network[D]. Wuhan: Huazhong University of Science and Technology,2008.
[4]林琪,李智.基于拓扑特征的卫星网络效能评估[J].中南大学学报(自然科学版),2013,44(S2):368-371.
LIN Q, LI Z. Evaluation of Satellite network performance based on topological characteristics[J]. Journal of Central South University(Natural Science Edition),2013,44(S-2):368-371.
[5]MILO R, SHEN-ORR S, ITZKOVITZ N,et al. Network motifs:simple building blocks of complex networks[J]. Science, 298(5594):824-827.
[6]CASALS M R, Corominas-Murtra B. Assessing european power grid reliability by means of topological measures[J]. OAI, 2009,121:527-537.
[7]PAUL S, JOBST H, KURTHS J,et al. Detours around basin stability in power networks[J].New Journal of Physics,2014,16(12):125001.
[8]孫晓伟. 基于网络模体的科学学数据研究[D].成都:电子科技大学,2019.
SUN X W. Scientific data research based on networkmotif[D]. Chengdu: University of Electronic Science and Technology of China,2019.
[9]高贺. 北斗导航系统星间链路分配方法研究[D].湖南:湖南大学,2018.
GAO H. Research on inter-satellite link allocation method of BDS[D]. Hunan: Hunan University,2018.
[10] 辜姣,郭龙,江健,等.多层网络和含时网络的相关问题研究[J].复杂系统与复杂性科学,2016,13(1):58-63,67.
GU J, GUO L, JIANG J, et al. Research on related problems of multilayer networks andtemporal networks[J]. Complex Systems and Complexity Science,2016,13(1):58-63,67.
[11] HOLME P, SARAMKI J. Temporal networks[J]. Physics Reports, 2012, 519(3):97-125.
[12] 覃桂敏.复杂网络模式挖掘算法研究[D]. 西安:西安电子科技大学, 2013.
QIN G M. Research on complex network pattern mining algorithm[D]. Xi′an: Xidian University, 2013.
[13] KASHTAN N, ITZKOVITZ S, MILO R, et al. Efficient sampling algorithm for estimating subgraph concentrations and detecting network motifs.[J]. Bioinformatics,2004,20(11):1746-1758.
[14] WERNICKE S, RASCHE F. FANMOD: a tool for fast network motif detection[J]. Bioinformatics,2006,22(9):1152-1153.
[15] SAEED O, FALK S, MASOUDI-NEJAD, et al. MODA: an efficient algorithm for network motif discovery in biological networks[J]. Genes & Genetic Systems,2009,84(5):385-395.
[16] TIEN H, SOMADINA M, KIM W, et al. NemoMap improved motifcentric network motif discovery algorithm[J]. Advances in Science, Technology and Engineering Systems,2018,3(5):186-199.
[17] SCHILLER B, JAGER S, HAMACHER K, et al. Strea m-a stream-based algorithm for counting motifs in dynamic graphs[C]// International Conference on Algorithms for Computational Biology. Mexico: Springer, Cham, 2015.
[18] EDIGER D, JIANG K, RIEDY J, et al. Massive streaming data analytics: a case study with clustering coefficients[C]// IEEE International Symposium on Parallel & Distributed Processing. Atlanta, Georgia, USA: IEEE, 2010.
[19] ASHWIN P, AUSTIN R B, JURE L. Motifs in temporal-networks[J].CoRR,2016,abs/1612.09259.
[20] SARPE I, VANDIN F. odeN: simultaneous approximation of multiple motif counts in large temporal networks[C]. Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Virtual Event. Queensland, Australia: 2021: 1568-1577.
[21] 刘天雄.GPS全球定位系统由几部分组成?[J].卫星与网络,2012(4):56-62.
LIU T X. How many parts does GPS system consist of? [J]. Satellite and Network,2012(4):56-62.
[22] 李朝瑞,孟新. 星座仿真中天线扫描范围对系统的影响分析[C]//中国空间科学学会空间探测专业委员会第十九次学术会议论文集(下册).宁波, 2006,2:433-437.
LI C R, MENG X. Analysis of the influence of antenna scanning range on the system in constellation simulation[C]//Proceedings of the 19th Academic Conference of the Space Exploration Professional Committee of the Chinese Society of Space Sciences 2. Ningbo, 2006, 2: 433-437.
(责任编辑 李 进)
收稿日期: 2022-04-07;修回日期:2022-06-20
基金项目: 复杂电子系统仿真重点实验室基础研究项目(DXZT-JC-ZZ-2020-001)
第一作者: 胡博仁(1999-),男,湖南宁乡人,硕士研究生,主要研究方向为复杂网络、系统科学。
通信作者: 裴忠民(1976-),男,山东济宁人,博士,副研究员,主要研究方向为计算机科学与技术、系统科学。
