复杂网络中的级联失效研究进展
2024-04-29张渡淯吴建军杨欣马智傲朱天雷
张渡淯 吴建军 杨欣 马智傲 朱天雷

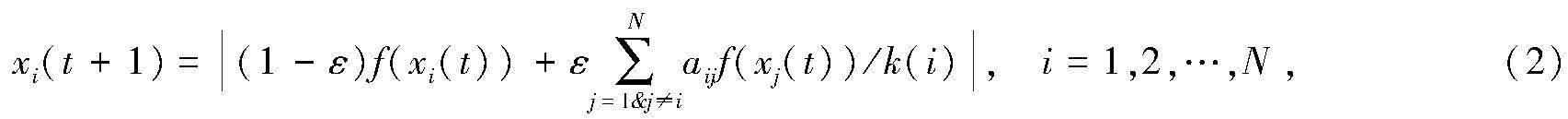
摘要:随着网络科学的发展和复杂系统理论的兴起,学者们开始对复杂网络的结构和动力学特性展开深入研究。在复杂网络动力学特征中,级联失效作为复杂网络动力学特征中重要的研究领域之一,描述了一个系统或过程中的一个故障或错误导致其他相关组件或环节的连锁反应性故障。学者们针对复杂网络中的级联失效提出了多种级联失效模型和恢复策略。本文对级联失效的发生机理进行了分析,总结了国内外针对复杂网络中级联失效的研究成果,并概括了应对级联失效的恢复策略,同时指出了现有研究存在的问题与不足之处,为未来的研究提供了一定的思路。
关键词:级联失效;复杂网络;多层网络;传播特性;恢复策略;渗流;网络鲁棒性
中图分类号:N945.17 文献标志码:A 文章编号:1002-4026(2024)02-0085-12
Research progress on cascading failures in complex networks
Abstract∶With the development of network science and the emergence of complex systems theory, scholars have embarked on in-depth research on the structural and dynamic properties of complex networks. Among the dynamic properties of complex networks, cascading failures, as one of the most important research areas, describe a situation where a fault or error in a system or process leads to the failures of other related components or links. Various models and recovery strategies have been proposed for cascading failures in complex networks. This study analyzes the mechanisms of cascading failures, provides a comprehensive summary on the development of domestic and international cascading failure in complex networks, outlines the recovery strategies for addressing cascading failures, and highlights the existing issues and shortcomings in current research, providing valuable insights for future studies.
Key words∶cascading failure; complex networks; multilayer networks; propagation properties; recovery strategies; percolation; network robustness
随着人类科学与技术的高速發展,如何描述复杂系统的结构与性质成为一个亟待解决的问题。自网络的无标度特性和小世界特性被发现以来[1-2],随着网络科学的不断发展完善,越来越多的学者使用复杂网络的概念与模型去描述复杂系统的结构与性质。复杂网络将系统中的组成部分定义为节点,组成部分之间的相互关系描述为连边,从而抽象化和数学化现实生活中许多的复杂系统。例如运用复杂网络理论,刻画人与人之间的社交关系[3],描述电力网络[4]、道路网络[5]、航空网络[6]等基础设施系统或是将其用于医学领域对神经网络[7]、药理科学[8]等问题进行研究。
在复杂网络研究中,网络中的动力学传播问题是一个十分重要的研究领域,无论在自然界或是人类社会中,大量的行为和现象都能够通过网络传播来影响网络中的各个组成部分。如传染病可以通过接触关联网络在人群中迅速传播,信息电流可以在大脑神经网络中进行传递,交通拥堵可以在道路网络中扩散等。在复杂网络的研究中,级联失效被认为是最重要的传播问题之一。级联失效用来描述在网络中一个或者几个节点或连边受到干扰或破坏时,其周围的部分受到连锁影响,导致干扰继续传播,最终整个系统可能因此功能失效,引发网络的灾难性崩溃。现实生活中的网络具有强耦合关联特性,这为级联失效的传播提供了更多的路径与选择,进而增加了网络的脆弱性[9]。以电力网络为例,电力网络中的一个组件故障或者损坏时,负载会传递到相邻的元件,如果相邻组件的负载超出其容量过载,就可能发生故障,从而引发级联失效现象,影响整个电力网络,严重时导致整个电力系统陷入瘫痪。2003年8月发生在美国和加拿大的大停电事件就是一个经典的级联失效案例。该事件导致美国东北部地区及加拿大东部地区出现大范围停电,四千万人受到影响,造成了大约270亿美元的经济损失[10]。因此,对网络中的级联失效现象进行研究,对于提高网络的鲁棒性至关重要[11]。
级联失效现象已经成为一个新兴且具有极大研究意义的跨学科研究方向,涵盖了计算机科学[12]、医学[13]、交通工程[14]、电气工程[15]与社会科学[16]等众多学科领域。研究网络中的级联失效不仅揭示了网络结构对级联失效传播的影响,更为重要的是,通过对级联失效进行提前的建模和模拟,可以减轻对网络的不利影响,提高网络的鲁棒性。在交通工程、电气工程等关键领域,对网络中级联失效现象的研究是网络鲁棒性研究的重要一环。对于级联失效真正的刻画需要首先明确其失效机理,然后在机理揭示的基础上进行复杂系统的级联失效建模,最后根据对失效影响范围和强度的定量分析,提出相应的快速恢复策略。鉴于此逻辑,本文主要归纳了不同复杂网络中级联失效的发生机理,回顾了级联失效现象在单层网络和多层网络中的传播特点,总结了几类主要的级联失效模型,以加深对级联失效现象的理解,同时着重探讨如何通过研究级联失效来提升网络的鲁棒性,以减轻或遏制级联失效带来的灾难性影响,这一研究方向对未来网络设计和管理具有重要的启发和指导作用。
1 级联失效机理
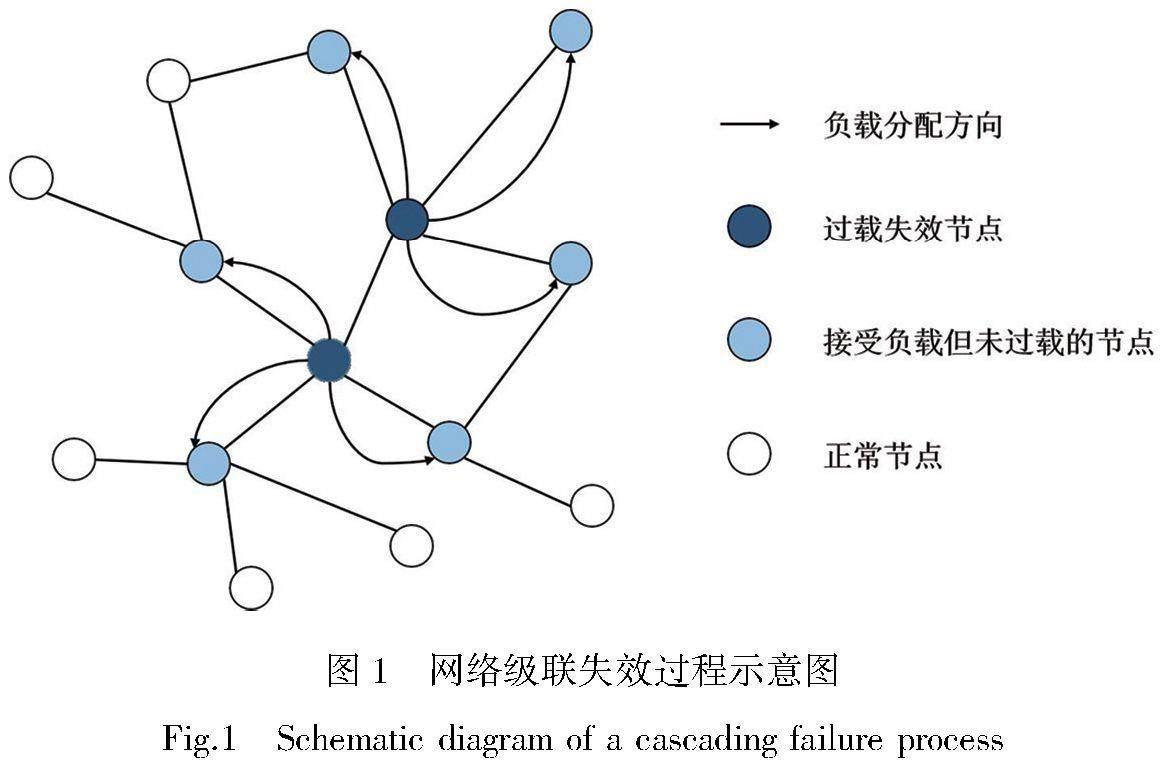
在现实生活中,级联失效现象最常见的发生机理为单个关键节点的过载,导致节点失效,如图1所示。随后,故障节点的负载会被重新分配到网络中的其他节点,这可能导致其他节点也超负荷运行。这种故障类似于雪崩效应,迅速而广泛地在网络中传播,直到所有节点都受到损害或系统失去大部分功能,无法正常运转。例如,在航空网络中,当通过节点或连边的流量超过其容量时,人员和货物需要在机场内部重新分配,这可能引发级联失效现象,导致整个机场无法正常运作[17]。类似地,互联网是一个全球性的网络,包括各种网络设备、路由器、交换机和光缆等。在互联网中,当某个网络节点或网络链路的负载过高或发生故障时,可能会导致周围节点或链路的负载增加,进而引发级联失效。针对这一现象,文献[18-19]进行了深入的调查与研究。其他级联失效现象的发生机理包括但不限于表1所示。
失效机理是复杂系统动力学过程研究的重要方向,是深入了解系统复杂性的重要手段,也是进行级联失效建模的基础和关键。虽然国际上对此方向的研究已有众多成果,但不可否认还存在大量的研究空白。事实上,真实网络中的级联失效机理非常复杂,涉及的要素及要素间的相互作用很难用一个统一的机理模型进行描述。因此,需要更多的研究結合研究网络对象的性质和特征,进行针对性的机理分析。此外,在机理的揭示和解释方面,深入挖掘大量数据,同时考虑不同研究对象的核心影响因素,结合大数据、人工智能等新技术,可以建立机理模型来揭示其演化规律,充分辨识影响源及其失效路径,从而对级联失效过程有更清晰的理解。
2 级联失效的建模与影响分析
自级联失效概念提出以来,已经针对不同的网络对象开展了大量的研究分析工作。特别是复杂网络及其动力学过程研究的兴起,进一步推动了对复杂系统中级联失效的研究。
2.1 单层网络级联失效建模
在单层网络中,对级联失效现象的研究,可以揭示不同类型的级联失效模型在不同网络中对系统功能和鲁棒性的影响。本节主要分析了单层网络中经典的三种级联失效模型及其在现实网络中的应用。
学者们已经提出了多种模型用以描述级联故障的机制。主要包括负荷-容量模型(节点动态模型、边动态模型、节点与边混合动态模型)、沙堆模型以及基于耦合映像格子的级联失效模型等。
在级联失效模型研究中,Motter等[26]于2002年提出的节点动态模型被广泛应用。该模型假设网络中的信息、能量等传输量沿着最短路径进行传输,因此节点处的负载通过节点的所有最短路径上的传输量总和来确定。节点的容量被定义为该节点理想的最大负载,假设节点j的容量Cj与其初始负载Lj满足式(1):
Cj=(1+α)Lj, j=1,2,…,N,(1)
其中常数α≥0是容忍参数,N为初始的节点数。当节点被移除后,最短路径的分布会发生变化,从而导致节点负载的改变。如果某些节点的负载增加并超过容量,则这些节点将发生故障,任何故障都会导致节点负载分布的变化,这个模型描述了级联失效的过程。同年,Holme等[27]考虑了在BA无标度网络中,优先连接过程中边的过载问题。因为节点动态模型只考虑节点的状态,没有考虑连边的动态行为,于是在2003年,Moreno等[28]正式提出了边动态模型,以BA无标度网络为例,研究了由于边的容量有限所引发的级联失效现象。2004年,Crucitti等[29]将节点动态模型与连边混合模型相结合,提出了考虑连边效率与最优路径的节点与边混合动态模型。该模型将级联失效的过程描述为当某个节点由于故障而失去特定的功能后,网络中节点之间的最优路径发生变化,导致负载重新分布,从而引发连续的故障。
在沙堆模型[30]中,沙子被随机撒放到沙堆上,导致一些位置发生塌陷,并将沙粒转移到相邻的塌陷位置。当堆的斜度超过一定阈值时,沙粒的放置引发雪崩,并可能进一步引发级联失效现象,影响许多其他位置。在临界状态下,沙堆坍塌规模的概率分布遵循幂律分布。沙堆模型适用于许多领域中的级联失效问题,如经济学[31]、地质学[32]等。Dobson等[33]研究发现,沙堆模型下的级联失效中失效节点的数量遵循扩展的准二项分布。
1984年,耦合映像格子(CML)[34]被首次提出用于描述时空混沌现象。由于CML模型能够描述丰富的时空动态行为,在2004年[35]被引入网络科学领域,用于研究不同耦合拓扑结构网络中的级联失效故障。考虑一个具有N个节点的CML模型,其表达式如下:
其中xi(t)表示第t个时间步第i个节点的状态变量,如果节点i与节点j之间存在连边,则aij=aji=1,否则aij=aji=0;k(i)表示为节点i的度;ε∈(0,1)表示耦合强度,函数f为混沌Logistic映射,即f(x)=4x(1-x)。如果节点i在第m个时间步处于正常状态,则0
此时节点i的状态xi(m)>1。在m+1时刻,与节点i相邻的节点会受到节点i的干扰,其状态值可能大于1,从而引起新一轮的节点故障。这个过程反复出现,导致级联失效现象的发生。
对拓扑网络进行级联失效的模拟分析可以更好地理解与分析网络结构与功能。在2002年,Watts[36]通过对随机网络上的级联失效进行研究,发现当网络足够稀疏时,级联失效对应的临界点呈幂律分布,并且最高度的节点在触发级联方面具有关键作用。Moreno等[37]研究BA无标度网络下的级联失效现象,指出为了防止级联失效现象的发生需要找到一个同时考虑网络本身的鲁棒性与能够预见网络崩溃的最佳标准。Xia等[38]在研究WS小世界网络中的级联失效时发现,级联失效现象中的鲁棒性与脆弱性主要与异构介数有关而与网络度分布无关。Mirzasoleiman等[39]在研究加权网络时提出了一种能提高网络鲁棒性,降低级联失效对网络影响的方法。Zhao等[40]为了了解级联失效如何在时间与空间上的传播,分析与数值研究了空间嵌入网络上级联失效现象的时空传播行为,发现级联失效从初始的故障中心会以恒定的速度径向传播。谢丰[41]等则是在考虑网络动态性的基础上,对级联失效条件下复杂网络的抗毁性能进行了研究。
在研究基于一般网络的级联失效现象时,学者们也广泛探索和研究了真实的现实网络。Carreras等[42]通过对发电机、输电网络以及一些组件进行限制,研究电力网络中的级联失效现象,确定了由输电线路流量限制和发电机能力限制的两种临界值。Wu等[43]通过研究无标度交通网络在不同移除策略下的级联失效现象,发现基于混合移除的方法可以减少级联失效的破坏并延迟网络的崩溃时间。同年,还考虑到交通量分配的用户均衡原则,研究了加权交通网络的级联失效现象[44]。基于北京城市轨道交通网络的数据,Sun[45]等考虑了静态客流加载与重新分配,并对CML模型进行了改进,通过改进模型能够识别关键站点,深入分析北京城市轨道交通网络脆弱性。在此基础上,Lu等[46]使用改进的CML模型对级联失效中的重要影响因素进行了量化,对轨道交通网络的脆弱性进行建模。除了在交通网络与电力网络的应用之外,社交网络[47]、金融网络[48]等真实网络中的级联失效现象也得到了广泛的研究,取得了较多的进展。
2.2 多层网络级联失效建模
目前大多数研究中,涉及的网络都是独立的单层网络,其中所有的连边只具有单一属性。然而,在现实生活中,仅使用单层网络难以准确描述一些复杂的现实网络,例如,在社交网络中,每个人拥有不同类型的社交关系,如朋友、同事、亲人等,从而抽象出不同的社交网络层[49]。同样的,在城市交通网络中,存在着多种不同类型的交通工具满足人们的出行需求,不同类型的交通工具可以被抽象为不同的交通网络层[50]。图2展示了按照3种不同类型的交通工具对马德里的交通网络进行了3层划分[51]。因此,为了更好地研究复杂系统,多层网络结构被引入到复杂系统的研究中。通过引入多层网络,研究者可以更全面地考虑网络中的多个层面和属性,从而更好地理解和分析复杂系统的行为和功能。
在现实生活中,存在着大量相互依存的多层网络,与孤立的单层网络相比,这些多层网络在面对蓄意攻击或随机扰动时会更加脆弱,具有较低的鲁棒性[52]。例如,由电力网络与通信网络组成的多层网络中,现代电力系统依赖通信网络进行控制,而通信网络则需要电力网络来维持自身正常的运行,一旦其中一层网络受到干扰,将对整个多层网络的稳定性造成干扰[53]。Vespignani[54]认为,在多层网络中,级联失效现象的传播具有极大的毁灭性,评估其对整个网络的影响具有极大的研究价值。当一个或多个节点或边在一个层面上失效时,这些失效可能会扩散到其他层,引发更广泛的级联失效。这种级联失效的传播可能导致整个多层网络的系统性崩溃,造成严重的后果。
尽管多层网络中的级联失效现象已经引起了许多研究者的关注,但在该问题上尚未形成统一的标准和定义。直到2010年,Buldyer等[55]提出了一个基于渗流模型的框架,用于描述相互连接的双层网络在面对级联失效时的鲁棒性。在该模型中,作者认为组成双层网络的网络A、B需要有相同的节点数N,并且两个网络中的所有节点之间都存在一对一的连边,即在该模型中,网络A的每个节点都依赖于网络B中的节点,反之亦然。当A层中的一组节点受到干扰故障时,与这些受到干扰节点相邻的B层节点也会受到影响发生故障。同时,在A层中,只有最大连通子图中的节点能够保证正常工作,其余节点全部失效。接下来,在B层中,最大连通子图中的节点保持正常工作而剩余节点全部失效。交替分析A层和B层,并迭代该算法,可以模拟级联失效现象从一层传播到另一层的过程。图3展示了双层网络中级联失效的具体过程。
在此基础上,Buldyer团队中的Gao等[56]、Shao等[57]将模型扩展到多个网络相互依存的多层网络(network of network)与部分相互依存的双层网络。他们发现,在依赖程度较低的双层网络面对级联失效现象时,极易受到一阶渗流相变解体的影响。同一团队的Li等[58]通过研究发现,在多层网络中,相互依存的节点之间的距离处于中间范围时,多层网络的脆弱性降低,故障更容易在网络中传播,从而导致级联失效现象的发生。Baxter等[59]研究了级联失效导致网络发生雪崩这一现象,确定了导致雪崩现象发生的临界情况的节点群,这些集群决定了级联失效对网络的破坏情况以及剩余网络的统计特性。Liu等[60]考虑渗流诱导下的多层网络的级联失效现象,并揭示了影响多层网络面对级联故障鲁棒性的因素,同时提供了一种设计或控制系统以达到期望鲁棒性水平的情况。Han等[61]将单层网络中的节点与边混合动态模型扩展到多层网络中,并对其进行改进,模拟结果表明多层网络的鲁棒性与容量呈正相关,而与负载呈负相关。通过这些研究,能够更好地理解多层网络中级联失效的传播机制和影响因素,进一步分析多层网络的性质。
同样的,学者们也广泛研究了现实生活中多层网络的级联失效现象。Rosato等[62]以意大利电力网络与通信网络组成的多层网络为基础,分别研究了因电力网络与通信网络受到干扰所引发的级联失效现象对多层網络性能造成的退化。他们发现在两个网络之间存在适度耦合的情况下,电力网络故障对通信网络的影响会显著放大。Zhang等[63]研究了由城市轨道交通网络、公交网络与其他交通方式网络组成的多层交通网络。他们考虑了在不同负载条件下不同故障产生的级联失效现象对多层交通网络的影响,并构建了一个稳定性分析模型用于分析级联失效情况下多层网络的稳定性。通过多个角度的分析,揭示了多层交通网络的稳定性特征。Naeini等[64]将城市基础设施网络抽象为多层网络,并提出了一种基于马尔科夫链的框架来模拟多层网络中的级联失效现象。该框架能描述两层网络之间的相互依赖性,以预测它们组成的多层网络对级联故障的恢复能力,并描述相互依赖对系统可靠性的影响。综上所述,学者们通过对现实生活中多层网络的级联失效现象进行研究,为理解多层网络的鲁棒性和稳定性提供了重要的见解。这些研究成果有助于指导设计和管理具有高可靠性的多层网络,以应对可能发生的级联失效风险。
目前用于描述级联失效现象的模型存在一定的局限性,无论是应用于单层网络还是多层网络的模型,都无法有效分析更加复杂的结构。随着科技的高速发展,出现了越来越多超级复杂巨系统,现有研究的深度远远不足。因此,有必要引入更多交叉学科领域的技术用于研究超级复杂巨系统中级联失效现象。例如,借鉴融合系统科学中的多系统理论,将系统分解为多个子系统,并研究子系统之间的相互作用和影响。通过对子系统之间的耦合关系和交互作用进行分析和建模,可以深入研究级联失效现象。这些新颖的技术可以为级联失效建模提供更加精细和准确的方法与手段,有效地分析超级复杂巨系统的鲁棒性与安全性。此外,失效建模需要针对不同的网络对象进行研究,同样很难找到一个普适性的、大一统的模型进行表示。因此,需要更多的研究去关注影响复杂网络级联失效的内部核心关键要素及其分解和交互作用。通过对这些要素进行建模和表征,以满足实际应用的需求。
2.3 级联失效对网络的影响分析
级联失效对网络的影响不仅在于其潜在的破坏性,更重要的是其对网络整体鲁棒性的挑战。网络鲁棒性是指网络系统对于各种内部或外部干扰、攻击或故障的抵抗能力,即网络在面对各种挑战时能够保持正常运行的能力[65]。在网络科学中,鲁棒性是一个关键的概念,它直接关系到网络的稳定性、可靠性和安全性。众多学者已对在面对级联失效情境下网络鲁棒性的问题展开了深入研究。Schneider等[66]考虑到级联失效的特性,提出了一种创新的复杂网络鲁棒性度量方法,用于评估网络在面对级联失效条件下的整体鲁棒性。该研究将网络的鲁棒性定义为η,其表达式见式(4):
其中T是基于级联失效攻击需要的总轮数,Ssum为网络最大连通子图的累计大小,t为级联失效的攻击次数,N为整个网络的总节点数。Ko等[67]提出了一种基于熵的方法,用于量化电力网络在应对级联故障时的鲁棒性。Zhang等[68]在研究中专注于城市轨道交通网络,基于网络的拓扑结构和功能特征,采用两种鲁棒性指标,分别考察网络边数量的变化和地铁网络的运行效率变化。将这两项指标综合考量,提出了一个综合的动态鲁棒性指标,用于评估城市轨道交通网络在级联失效背景下的鲁棒性表现。此外,周琴等[69]则通过模拟开发者协作网络中的级联失效现象,利用相对最大连通子图和网络的剩余负载率两个指标,从网络结构和功能两个方面来描述网络的鲁棒性特征。这些研究为深入理解级联失效对网络鲁棒性的影响提供了重要的学术贡献。
持续深入研究和评估级联失效对网络鲁棒性的影响对确保网络系统的稳定运行和持续发展至关重要。只有不断提升网络的鲁棒性水平,才能更好地保护网络系统免受级联失效带来的各种威胁和风险的侵害,确保网络在面临挑战时能够稳健应对,持续发挥其重要作用。未来技术的不断发展将为网络鲁棒性研究带来新的机遇和挑战。人工智能、物联网和区块链等新技术的应用将为网络系统设计和运行方式带来革新,有助于更准确地分析网络结构、预测潜在的级联失效路径,并实现智能化的网络管理和应急响应。未来技术的推动也将促进跨学科合作,促使不同领域的专家共同探讨级联失效对网络鲁棒性的影响,推动网络系统适应未来挑战的发展和优化。
3 级联失效恢复策略
尽管在过去的近二十年中,级联失效现象得到了广泛的研究,但如何在级联失效发生前制订计划以及减轻级联效应的影响并预防系统的崩溃也成为了学界关注的重点[70]。近年来,来自不同领域的学者开始致力于制定策略,提出有意义的方法去解决上述问题。Motter[71]在2004年首次提出了一种削弱因级联失效引起全局故障的策略,即在受到初始故障后,选择性地移除某些节点和连边,以大幅度减少级联失效的规模。以本篇综述为基础,应对级联失效的恢复策略大多是针对节点和连边两个方面制订恢复策略,本节将回顾这两种策略,从不同的角度去了解如何减轻级联失效的影响并避免网络崩溃。
3.1 减少过载
Liu等[72]提出了一种基于自愈机制的减轻由于过载引起的级联失效的策略。作者引入了一种针对过载传播的自愈模型,并在同质(ER随机网络)与异构(BA无标度网络)网络上研究了该模型在减轻级联失效方面的恢复作用。结果表明,相似的恢复特性对不同的拓扑性质的网络会产生不同的自愈效果。Zhang等[73]针对多层网络中的级联失效现象进行了模拟研究,探讨了每层网络耦合的最佳范围,即网络分配给其他网络的负载,以最大限度地提高多层网络的鲁棒性。Ouyang等[74]结合实际网络以电力网络为例,将网络受到级联失效的影响分为三个阶段:抵抗阶段、吸收阶段和恢复阶段,并提出了强化关键部件的容量、减少负载量等措施有效应对级联失效现象的建议。
3.2 修复节点
Wang[75]提出了4种修复策略,分别为:对负载最高的节点进行缓解(MHL);对最低负载的节点进行缓解[76](MLL);对那些邻居节点故障更有可能触发其自身故障的节点进行缓解(MHHC)和那些自身故障更有可能導致邻居节点故障的节点进行缓解(MHC)。通过研究这4种策略对BA无标度网络在面对级联失效现象时提高网络鲁棒性的效率,作者认为在面对较大尺度的级联失效现象时,MHL是最有效的方法,而在面对较小尺度的级联失效现象时,MHHC和MHC比MHL与MLL更有作用。在此基础上,Stippinger等[77]提出了一种在双层网络中的级联失效恢复模型,旨在减轻系统中级联失效所带来的故障。该模型的思路为使用受影响节点邻居节点新的连边替换节点发生故障时失效的连边。La rocca等[78]则是采用随机概率将失效的节点重新连接到最大连通子图中以恢复节点功能,并发现该策略在应用于平均度较低的网络时最为有效,网络对于级联失效的鲁棒性较强。唐亮等[79]构建了节点故障概率随故障次数增加而逐渐降低的故障概率函数,考虑节点具有恢复和重复失效等特点,设计了概率恢复与阶段恢复两种节点恢复策略,建立了节点恢复条件下的级联失效模型。
隨着云计算、大数据、人工智能等技术的不断发展,未来的系统将变得越来越复杂和庞大,级联失效的风险也将随之增加。因此,针对级联失效的恢复策略需要不断地进行优化和升级,在未来与强化学习、自动控制等不同学科交叉融合,不断地研究和开发新的技术和工具,以适应不断变化的系统环境和业务需求。此外,复杂系统的恢复过程涉及元素众多,是一个真正意义上的大规模、强关联系统优化问题。在模型特别是算法方面,仍然存在大量的研究挑战。同时,结合大模型,实现对失效的快速恢复也将成为一个重要的研究领域。
4 总结与展望
级联失效是复杂网络动力学研究方向中最重要的研究内容之一,它揭示了扰动如何引发进一步的失效,并可能导致全局规模的突变。对级联失效的主要理论与应用进行梳理后,本文对其发生机理进行了总结与分析。此外,本文着重介绍了三类常用的单层网络级联失效模型,并对这些模型在真实网络中的应用进行了分析。同时,本文明确了对多层网络进行研究的重要性,指出多层网络相较于单层网络更为脆弱,发生级联失效的后果更加严重,并对多层网络中的级联失效模型进行了总结。本文还总结了级联失效对网络特别是鲁棒性的影响。在应对级联失效的恢复策略方面,本文将目前的研究工作分为了减少过载与修复节点两种不同侧重点的恢复策略。结合已有研究进展,从以下方面提出对未来研究的建议:
(1)尽管现有的级联失效模型在理论上具有一定的可行性和实用性,但它们都缺乏精细的建模,研究模型偏理想化,因此需要更加贴近实际情况的级联失效模型。可以基于数据分析和深度学习等技术,在多重数据的驱动下,建立适用于不同场景的更智能化、精细化级联失效模型。
(2)现有的对多层网络中级联失效的研究普遍集中在双层的相互依存网络,很少有学者对两层以上的多层网络进行研究与分析。此外,对多层网络中的级联失效现象进行建模时,学者普遍使用渗流理论中的模型进行仿真计算,极少有学者从多层网络中故障产生与传播机制出发来建立级联失效模型。因此,在未来的研究中,需要建立更贴近实际情况的级联失效模型,以更好地模拟多层网络甚至更复杂的系统中的故障传播过程。
(3)针对级联失效的恢复策略的研究仍处于起步阶段,需要进一步改进,并需发展准确、高效的模型和算法以提高网络的鲁棒性和可靠性,以应对潜在的系统崩溃和灾难性的影响。如结合多智能体控制的方法,可以训练针对所有网络更加普适的级联失效恢复策略,甚至可以利用该技术设计出具有更强鲁棒性的复杂网络。
随着复杂网络理论的不断完善和发展,针对不断出现的问题,进一步改进和发展准确、高效的模型和算法对于理解和应对复杂网络中的级联失效现象至关重要。这将有助于提高网络的鲁棒性和可靠性,以应对潜在的系统崩溃和灾难性的影响。同时也希望引导读者关注一些与该领域密切相关的问题和难题,相信这些问题很可能会迅速引起专家学者们的关注,并得到有效地解决。
参考文献:
[1]BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. DOI: 10.1126/science.286.5439.509.
[2]WATTS D J, STROGATZ S H. Collective dynamics of ‘small-world networks[J]. Nature, 1998, 393: 440-442. DOI: 10.1038/30918.
[3]GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826. DOI: 10.1073/pnas.122653799.
[4]曹一家, 陈晓刚, 孙可. 基于复杂网络理论的大型电力系统脆弱线路辨识[J]. 电力自动化设备, 2006, 26(12): 1-5. DOI: 10.3969/j.issn.1006-6047.2006.12.001.
[5]吴建军, 李树彬. 基于复杂网络的城市交通系统复杂性概述[J]. 山东科学, 2009, 22(4): 68-73.
[6]吴晋峰, 任瑞萍, 韩立宁, 等. 中国航空国际网络结构特征及其对入境旅游的影响[J]. 经济地理, 2012, 32(5): 147-152. DOI: 10.15957/j.cnki.jjdl.2012.05.025.
[7]HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI: 10.1126/science.1127647.
[8]韩利文, 陈善军, 董榕, 等. 网络药理学在中药复杂作用模式研究中的应用进展[J]. 山东科学, 2021, 34(6): 22-31. DOI: 10.3976/j.issn.1002-4026.2021.06.004.
[9]SUN H J, ZHAO H, WU JJ. A robust matching model of capacity to defense cascading failure on complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2008, 387(25): 6431-6435. DOI: 10.1016/j.physa.2008.07.028.
[10]MASSEY G W. The impact of installing power factor improvement capacitors: an overview and case study[C]//Proceedings of Rural Electric Power Conference. Fort Worth, TX, USA. IEEE, 2002: C4. DOI: 10.1109/REPCON.1996.495245.
[11]WU J J, GAO Z Y, SUN H J, et al. Congestion in different topologies of traffic networks[J]. Europhysics Letters, 2006, 74(3): 560-566. DOI: 10.1209/epl/i2005-10551-x.
[12]LI D H, WANG Q, ZHANG X, et al. Predicting the cascading failure propagation path in complex networks based on attention-LSTM neural networks[C]//2023 IEEE International Symposium on Circuits and Systems (ISCAS). Monterey: IEEE, 2023: 1-4. DOI: 10.1109/ISCAS46773.2023.10181599.
[13]JONES D T, KNOPMAN D S, GUNTER J L, et al. Cascading network failure across the Alzheimers disease spectrum[J]. Brain, 2016, 139(2): 547-562. DOI: 10.1093/brain/awv338.
[14]高自友, 吴建军. 出行者博弈、网络结构与城市交通系统复杂性[J]. 复杂系统与复杂性科学, 2010, 7(4): 55-64. DOI: 10.13306/j.1672-3813.2010.04.006.
[15]REIS S D S, HU Y Q, BABINO A, et al. Avoiding catastrophic failure in correlated networks of networks[J]. Nature Physics, 2014, 10: 762-767. DOI: 10.1038/nphys3081.
[16]REN W D, WU J J, ZHANG X, et al. A stochastic model of cascading failure dynamics in communication networks[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 65(5): 632-636. DOI: 10.1109/TCSII.2018.2822049.
[17]CUMELLES J, LORDAN O, SALLAN J M. Cascading failures in airport networks[J]. Journal of Air Transport Management, 2021, 92: 102026. DOI: 10.1016/j.jairtraman.2021.102026.
[18]陈志龙, 郭平, 蒋银华, 等. 計算机网络级联失效建模与分析[J]. 后勤工程学院学报, 2012, 28(4): 85-90. DOI: 10.3969/j.issn.1672-7843.2012.04.015.
[19]吴杏, 曾康铭. 基于熵方法的计算机网络脆弱性检测和优化[J]. 微电子学与计算机, 2016, 33(7): 98-101. DOI: 10.19304/j.cnki.issn1000-7180.2016.07.021.
[20]黄英艺,金淳. 物流基础设施网络级联失效下的抗毁性分析[J]. 控制与决策, 2014,29(9):1711-1714.
[21]LIU H R, DONG M R, YIN R R, et al.Cascading failure in the wireless sensor scale-free networks[J]. Chinese Physics B, 2015, 24(5): 050506. DOI: 10.1088/1674-1056/24/5/050506.
[22]DAVID A E, GJORGIEV B, SANSAVINI G. Quantitative comparison of cascading failure models for risk-based decision making in power systems[J]. Reliability Engineering & System Safety, 2020, 198: 106877. DOI: 10.1016/j.ress.2020.106877.
[23]YI C Q, BAO Y Y, JIANG J C, et al. Mitigation strategy against cascading failures on social networks[J]. China Communications, 2014, 11(8): 37-46. DOI: 10.1109/CC.2014.6911086.
[24]XU J, WANG X F. Cascading failures in scale-free coupled map lattices[C]//2005 IEEE International Symposium on Circuits and Systems (ISCAS). Kobe: IEEE, 2005: 3395-3398. DOI: 10.1109/ISCAS.2005.1465357.
[25]ZHANG L, XU M, WANG S A. Quantifying bus route service disruptions under interdependent cascading failures of a multimodal public transit system based on an improved coupled map lattice model[J].Reliability Engineering & System Safety, 2023, 235: 109250. DOI: 10.1016/j.ress.2023.109250.
[26]MOTTER A E, LAI Y C. Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66(6): 065102. DOI: 10.1103/physreve.66.065102.
[27]HOLME P, KIM B J. Vertex overload breakdown in evolving networks[J].Physical Review E, 2002, 65(6): 066109. DOI: 10.1103/physreve.65.066109.
[28]MORENO Y, PASTOR-SATORRAS R, VZQUEZ A, et al.Critical load and congestion instabilities in scale-free networks[J]. Europhysics Letters, 2003, 62(2): 292-298. DOI: 10.1209/epl/i2003-00140-7.
[29]CRUCITTI P, LATORA V, MARCHIORI M. Model for cascading failures in complex networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2004, 69(4Pt 2): 045104. DOI: 10.1103/PhysRevE.69.045104.
[30]BAK P, TANG C, WIESENFELD K. Self-organized criticality: an explanation of the 1/f noise[J]. Physical Review Letters, 1987, 59(4): 381-384. DOI: 10.1103/PhysRevLett.59.381.
[31]張晓莉, 严广乐. 基于沙堆模型的股市脆性[J]. 哈尔滨工业大学学报, 2009, 41(10): 269-271. DOI: 10.3321/j.issn: 0367-6234.2009.10.060.
[32]姚令侃, 黄艺丹, 杨庆华. 地震触发崩塌滑坡自组织临界性研究[J]. 四川大学学报(工程科学版), 2010, 42(5): 33-43. DOI: 10.15961/j.jsuese.2010.05.012.
[33]DOBSON I, CARRERAS B A, NEWMAN D E. A probabilistic loading-dependent model of cascading failure and possible implications for blackouts[C]//36th Annual Hawaii International Conference on System Sciences, 2003. Proceedings of the. Big Island: IEEE, 2003: 10. DOI: 10.1109/HICSS.2003.1173909.
[34]KANEKO K. Period-doubling of kink-antikink patterns,quasiperiodicity in antiferro-like structures and spatial intermittency in coupled logistic lattice:towards a prelude of a field-theory of chaos [J]. Progress of Theoretical Physics, 1984, 72(3): 480-486. DOI: 10.1143/PTP.72.480.
[35]WANG X F, XU J. Cascading failures in coupled map lattices[J]. Physical Review E, 2004, 70(5):056113.
[36]WATTS D J. A simple model of global cascades on random networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(9): 5766-5771. DOI: 10.1073/pnas.082090499.
[37]MORENO Y, GMEZ J B, PACHECO A F. Instability of scale-free networks under node-breaking avalanches[J].Europhysics Letters, 2002, 58(4): 630-636. DOI: 10.1209/epl/i2002-00442-2.
[38]XIA Y X, FAN J, HILL D. Cascading failure in Watts-Strogatz small-world networks[J]. Physica A: Statistical Mechanics and Its Applications, 2010, 389(6): 1281-1285. DOI: 10.1016/j.physa.2009.11.037.
[39]MIRZASOLEIMAN B, BABAEI M, JALILI M, et al. Cascaded failures in weighted networks[J]. Physical Review E, 2011, 84(4): 046114. DOI: 10.1103/physreve.84.046114.
[40]ZHAO J C, LI D Q, SANHEDRAI H, et al.Spatio-temporal propagation of cascading overload failures in spatially embedded networks[J]. Nature Communications, 2016, 7: 10094. DOI: 10.1038/ncomms10094.
[41]謝丰, 程苏琦, 陈冬青, 等. 基于级联失效的复杂网络抗毁性[J]. 清华大学学报(自然科学版), 2011, 51(10): 1252-1257. DOI: 10.16511/j.cnki.qhdxxb.2011.10.001.
[42]CARRERAS B A, LYNCH V E, DOBSON I, et al.Critical points and transitions in an electric power transmission model for cascading failure blackouts[J]. Chaos, 2002, 12(4): 985-994. DOI: 10.1063/1.1505810.
[43]WU J J, GAO Z Y, SUN H J. Effects of the cascading failures on scale-free traffic networks[J]. Physica A: Statistical Mechanics and Its Applications, 2007, 378(2): 505-511. DOI: 10.1016/j.physa.2006.12.003.
[44]WU J J, SUN H J, GAO Z Y. Cascading failures on weighted urban traffic equilibrium networks[J]. Physica A: Statistical Mechanics and Its Applications, 2007, 386(1): 407-413. DOI: 10.1016/j.physa.2007.08.034.
[45]SUN L S, HUANG Y C, CHEN Y Y, et al. Vulnerability assessment of urban rail transit based on multi-static weighted method in Beijing, China[J]. Transportation Research Part A: Policy and Practice, 2018, 108: 12-24. DOI: 10.1016/j.tra.2017.12.008.
[46]LU Q C, ZHANG L, XU P C, et al. Modeling network vulnerability of urban rail transit under cascading failures: a coupled map lattices approach[J]. Reliability Engineering & System Safety, 2022, 221: 108320. DOI: 10.1016/j.ress.2022.108320.
[47]YI C Q, BAO Y Y, JIANG J C, et al. Modeling cascading failures with the crisis of trust in social networks[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 436: 256-271. DOI: 10.1016/j.physa.2015.05.030.
[48]马亚男, 李莹. 商业银行集团客户成员企业信用风险传导仿真研究[J]. 商业研究, 2016(12): 96-101. DOI: 10.13902/j.cnki.syyj.2016.12.013.
[49]DE ARRUDA G F, RODRIGUES F A, MORENO Y. Fundamentals of spreading processes in single and multilayer complex networks[J]. Physics Reports-Review Section of Physics Letters, 2018, 756:1-59.
[49]DE ARRUDA G F, RODRIGUES F A, MORENO Y. Fundamentals of spreading processes in single and multilayer complex networks[J]. Physics Reports, 2018, 756: 1-59. DOI: 10.1016/j.physrep.2018.06.007.
[50]ALETA A, MELONI S, MORENO Y. A Multilayer perspective for the analysis of urban transportation systems[J]. Scientific Reports, 2017, 7: 44359. DOI: 10.1038/srep44359.
[51]ALETA A, MORENO Y. Multilayer networks in a nutshell[J]. Annual Review of Condensed Matter Physics, 2019, 10: 45-62. DOI: 10.1146/annurev-conmatphys-031218-013259.
[52]DE DOMENICO M. More is different in real-world multilayer networks[J]. Nature Physics, 2023, 19: 1247-1262. DOI: 10.1038/s41567-023-02132-1.
[53]WANG Z Y, CHEN G, LIU L, et al. Cascading risk assessment in power-communication interdependent networks[J].Physica A: Statistical Mechanics and Its Applications, 2020, 540: 120496. DOI: 10.1016/j.physa.2019.01.065.
[54]VESPIGNANI A. Complex networks: the fragility of interdependency[J]. Nature, 2010, 464(7291): 984-985. DOI: 10.1038/464984a.
[55]BULDYREV S V, PARSHANI R, PAUL G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464: 1025-1028. DOI: 10.1038/nature08932.
[56]GAO J X, BULDYREV S V, STANLEY H E, et al. Networks formed from interdependent networks[J]. Nature Physics, 2012, 8: 40-48. DOI: 10.1038/nphys2180.
[57]SHAO J, BULDYREV S V, HAVLIN S, et al. Cascade of failures in coupled network systems with multiple support-dependence relations[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 83(3 Pt 2): 036116. DOI: 10.1103/PhysRevE.83.036116.
[58]LI W, BASHAN A, BULDYREV S V, et al. Cascading failures in interdependent lattice networks: the critical role of the length of dependency links[J]. Physical Review Letters, 2012, 108(22): 228702. DOI: 10.1103/PhysRevLett.108.228702.
[59]BAXTER G J, DOROGOVTSEV S N, GOLTSEV A V, et al. Avalanche collapse of interdependent networks[J]. Physical Review Letters, 2012, 109(24): 248701. DOI: 10.1103/PhysRevLett.109.248701.
[60]LIU R R, JIA C X, LAI Y C. Asymmetry in interdependence makes a multilayer system more robust against cascading failures[J]. Physical Review E, 2019, 100: 052306. DOI: 10.1103/PhysRevE.100.052306.
[61]HAN H Y, YANG R N. Improvement on load-induced cascading failure in asymmetrical interdependent networks: modeling and analysis[J]. Mathematical Problems in Engineering,2015, 2015: 194568. DOI: 10.1155/2015/194568.
[62]ROSATO V, ISSACHAROFF L, TIRITICCO F, et al. Modelling interdependent infrastructures using interacting dynamical models[J]. International Journal of Critical Infrastructures, 2008, 4(1/2): 63. DOI: 10.1504/ijcis.2008.016092.
[63]ZHANG L, WEN H Y, LU J, et al. Exploring cascading reliability of multi-modal public transit network based on complex networks[J]. Reliability Engineering & System Safety, 2022, 221: 108367. DOI: 10.1016/j.ress.2022.108367.
[64]RAHNAMAY-NAEINI M, HAYAT M M. Cascading failures in interdependent infrastructures: an interdependent markov-chain approach[J]. IEEE Transactions on Smart Grid, 2016, 7(4): 1997-2006. DOI: 10.1109/TSG.2016.2539823.
[65]吳建军. 城市交通网络拓扑结构复杂性研究[D]. 北京: 北京交通大学, 2008.
[66]SCHNEIDER C M, MOREIRA A A, ANDRADE J S Jr, et al. Mitigation of malicious attacks on networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(10): 3838-3841. DOI: 10.1073/pnas.1009440108.
[67]KO Y, WARNIER M, KOOIJ R E, et al. An entropy-based metric to quantify the robustness of power grids against cascading failures[J]. Safety Science, 2013, 59: 126-134. DOI: 10.1016/j.ssci.2013.05.006.
[68]ZHANG Y F, NG S T. Robustness of urban railway networks against the cascading failures induced by the fluctuation of passenger flow[J]. Reliability Engineering & System Safety, 2022, 219: 108227. DOI: 10.1016/j.ress.2021.108227.
[69]周琴,徐桂琼.基于动态级联失效的开发者协作网络鲁棒性研究[J/OL].复杂系统与复杂性科学(2023-12-07).http://kns.cnki.net/kcms/detail/37.1402.N.20231207.1017.006.html.
[70]MAJDANDZIC A, PODOBNIK B, BULDYREV S V, et al. Spontaneous recovery in dynamical networks[J]. Nature Physics, 2014, 10: 34-38. DOI: 10.1038/nphys2819.
[71]MOTTER A E. Cascade control and defense in complex networks[J]. Physical Review Letters, 2004, 93(9): 098701. DOI: 10.1103/PhysRevLett.93.098701.
[72]LIU C R, LI D Q, FU B W, et al. Modeling of self-healing against cascading overload failures in complex networks[J].Europhysics Letters, 2014, 107(6): 68003. DOI: 10.1209/0295-5075/107/68003.
[73]ZHANG Y R, ARENAS A, YA[KG-*3]G[DD(-*2]ˇ[DD)][KG-*5]AN O. Cascading failures in interdependent systems under a flow redistribution model[J]. Physical Review E, 2018, 97: 022307. DOI: 10.1103/PhysRevE.97.022307.
[74]OUYANG M, DUEAS-OSORIO L, MIN X. A three-stage resilience analysis framework for urban infrastructure systems[J]. Structural Safety, 2012, 36/37: 23-31. DOI: 10.1016/j.strusafe.2011.12.004.
[75]WANG J W. Mitigation strategies on scale-free networks against cascading failures[J]. Physica A: Statistical Mechanics and Its Applications, 2013, 392(9): 2257-2264. DOI: 10.1016/j.physa.2013.01.013.
[76]WANG J W, RONG L L. Robustness of the western United States power grid under edge attack strategies due to cascading failures[J]. Safety Science, 2011, 49(6): 807-812. DOI: 10.1016/j.ssci.2010.10.003.
[77]STIPPINGER M, KERTSZ J. Enhancing resilience of interdependent networks by healing[J]. Physica A: Statistical Mechanics and Its Applications, 2014, 416: 481-487. DOI: 10.1016/j.physa.2014.08.069.
[78]LA ROCCA C E, STANLEY H E, BRAUNSTEIN L A. Strategy for stopping failure cascades in interdependent networks[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 508: 577-583. DOI: 10.1016/j.physa.2018.05.154.
[79]唐亮, 焦鹏, 李纪康, 等. 带恢复策略的复杂网络级联失效机理及鲁棒性研究[J]. 控制与决策, 2018, 33(10): 1841-1850. DOI: 10.13195/j.kzyjc.2017.0728.
