复杂系统可靠性

刘一萌 白铭阳 张小可 李大庆

摘要：随着科学技术的发展，社会技术系统的体系化、网络化、智能化程度逐渐加深，形成系统的复杂性。这些复杂系统的“故障”，诸如交通拥堵、谣言传播、金融崩溃，可以看作是一种“1+1<2”的系统能力负向涌现，难以直接通过系统单元的还原解析来理解，这对原有可靠性理论提出了挑战。现有复杂系统可靠性的研究主要从故障规律展开，从两个角度出发进行，一是考虑故障传播的系统脆弱性研究；二是考虑故障恢复的系统适应性研究。系统脆弱性研究的重点在于挖掘系统崩溃的内在机理，即故障的传播机理。系统适应性研究的重点关注于系统适应恢复能力，包括系统故障恢复机理。在此基础上，本文介绍了相关的可靠性方法研究。

关键词：复杂系统；可靠性；脆弱性；适应性

中图分类号：N945   文献标志码：A   文章编号：1002-4026（2024）02-0074-11

Complex system reliability

Abstract∶With the development of science and technology， the systematization， networking and intelligentization of the social technology system gradually deepen， forming the complexity of the system. The failures of these complex systems， such as traffic jams， rumor spreading， and financial collapse， can be regarded as a kind of "1+1<2" negative emergence of system capability， which is difficult to understand directly through the reduction analysis of system components. It challenges the classical reliability theory. Research on the complex systems reliability mainly focuses on failures laws， which includes two perspectives. One is the study of system vulnerability considering failure propagation. The other is the study of system adaptability considering failure recovery. System vulnerability studies focus on exploring the internal mechanism of system collapse， namely the failure propagation mechanism. System adaptability studies focus on the capacity to adapt and recover， including the system failure recovery mechanism. Based on this， the article introduces relevant research on reliability method.

Key words∶complex system; reliability; vulnerability; adaptability

复杂系统具有涌现性，难以简单地由单元的规律推理得到整体的规律[1-2]。系统工程为构建复杂社会技术系统提供指导，并被广泛应用于各个工业部门中。在钱学森等老一辈领军学者带领下，我国的系统科学和工程取得较大发展，从工程系统走向社会系统，提出开放的复杂巨系统方法论[3]及其实践形式[4]。近年来，系统学内涵得到不断深化并形成丰富理论成果[5-12]，在社會管理[13]、应急救援[14]、农业[15-16]、交通运输[17-18]等各领域均做出积极贡献。在系统工程方法论与技术上，我国学者提出的WSR（物理-事理-人理）方法论[19]、灰色系统方法[20]、TEI@I方法论[21]等都在国内外产生了一定影响。

基于火箭及计算机的工程实践，Lusser、冯·诺伊曼等人指出随着系统越来越复杂，可靠性成为了决定社会技术系统能否成功运行的关键问题[22-23]，可靠性学科随之迅速发展。20世纪90年代，可靠性系统工程理论被提出[24]，进而学者们又进一步细化了可靠性系统工程理论并提出其技术框架[25]。近几年，系统复杂性随着信息技术和智能技术的进步而不断提高。一方面，这种复杂性给系统带来了脆弱性挑战，系统出现了不同于简单系统的故障模式，形成了“1+1<2”的负向涌现。例如复杂系统内单元之间存在故障耦合，这使得少量单元的故障可能引发级联失效，导致整个系统崩溃。另一方面，复杂性也可能带来系统的适应性，可使系统具备从扰动中恢复和适应的能力。例如生态系统中物种多样性[26]、内稳态机制[27]、共生网络的嵌套性[28]等在增加了系统复杂度的同时，也使得种群和个体能在各种各样的风险挑战和环境变化下幸存。

传统可靠性方法是在元件数相对较少、元件间关系较为简单的系统上发展起来的，难以适用于分析复杂系统的可靠性。为此想要解决这些复杂系统的可靠性问题，必须借助系统科学研究和发展新理论、新方法应对新挑战。可靠性系统工程的实质是与故障做斗争，通过研究有关故障的规律，从而基于故障规律对故障进行事前预防和事后修理[24]。对复杂系统可靠性的研究也需要围绕其特有故障机理展开。系统可能因故障扩散而全面崩溃，也可能因故障恢复而稳定维持自身性能。因此可将复杂系统可靠性研究分为考虑故障传播的系统脆弱性研究和考虑故障恢复的系统适应性研究两类。

1 考虑故障传播的系统脆弱性研究

系统脆弱性是指系统被干扰后容易发生全局性崩溃的性质，一些具有罕见性、突发性等特点的重大事件往往是引发系统崩溃的原因之一。这类事件通常危害性高且迅速发生，后果严重并且难以预测。最为常见的导致系统发生全局性崩溃的原因是故障在系统中的传播。识别故障传播的机制和途径，有助于减少系统故障，降低系统脆弱性并提高可靠性。

1.1 复杂网络渗流理论

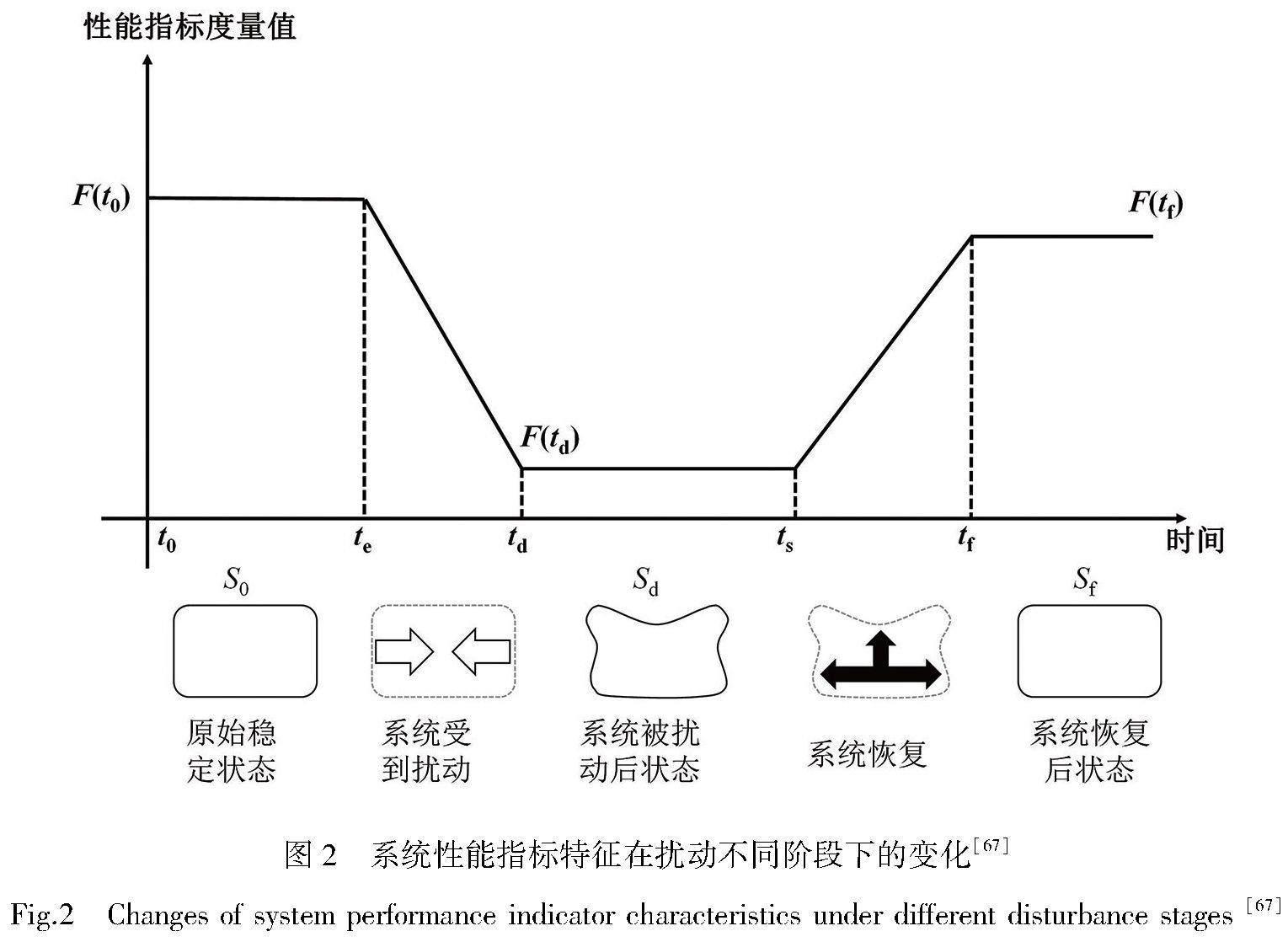
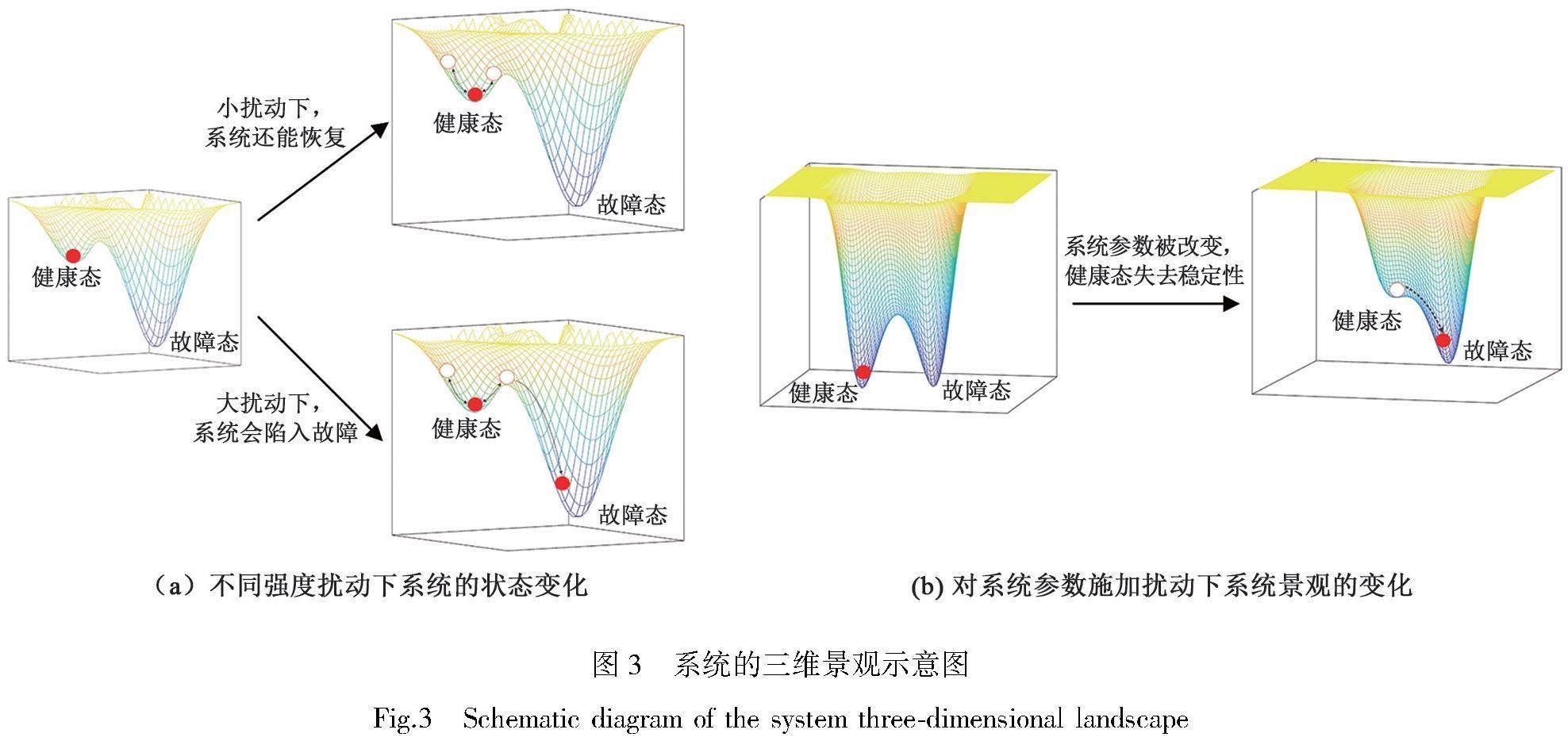
对故障传播的研究可以基于复杂网络渗流理论。渗流属于几何相变现象[29]，统计物理中的渗流理论[30]定量地刻画了网络整体层面的连通性丧失。在渗流过程中，网络的节点/连边被逐步移除，导致最大连通子团规模（其度量了网络连通性）降低。网络节点/连边移除的方法包括逐步随机移除节点/连边，或给定某属性的阈值，通过提高阈值来逐步移除属性低于阈值的节点/连边等。渗流过程中存在临界点，称为渗流阈值，在临界点附近，最大连通子团统计上变为0。以交通网络为例[31]（如图1所示），该研究对每条连边（道路）计算了当前道路车速与最大限速的比例 （r）。对于给定的阈值q，每条道路可以被分为功能正常的道路（r>q）和故障的道路（r

1.2 故障传播机理

利用渗流理论对系统故障传播机理进行研究主要关注系统的扰动模式以及故障传播方式。系统的扰动模式是指故障出现的方式，主要包括随机扰动和蓄意攻击两类。故障传播方式主要指故障的扩散方式，包括传染病故障模型和级联失效模型等。下面主要介绍以上两种扰动模式和两种传播方式。

1.2.1 系统的扰动模式

随机扰动是指节点/连边的故障在复杂网络中随机产生。研究发现随机扰动下的无标度网络具有优于随机网络的鲁棒性[32]。无标度网络是一种度分布（即对复杂网络中节点度数的总体描述）服从或者接近幂律分布P（k）～k-α的复杂网络[33]。理论推导和数值仿真表明幂律分布的参数α<3的无标度网络在随机攻击下难以解体[34]。此外研究还发现，像互联网这种度分布近似为幂律分布的复杂网络，虽然对于随机删除节点这种攻击具有高度鲁棒性，但是针对蓄意攻击却相对脆弱。

蓄意攻击是指挑选复杂网络中具有度数高、介数高等特征的重要节点，或权重高、重要度高的重要连边进行攻击使其故障的扰动方式。在蓄意攻击下，如果按照度的大小顺序来移除节点，无标度网络只要删除极少数的中心节点就会崩溃，比随机网络更加脆弱[32]。这也表明了无标度网络的高度异质性，即大部分连边集中于中心节点处。除了基于节点度数的攻击策略外，许多研究也基于其他原则的攻击策略分析故障传播，例如介数或基于其他不同中心性的攻击策略[35]。

1.2.2 系统的故障传播方式

常见的系统故障传播模型主要有传染病模型和级联失效模型。传染病模型是一种引入复杂网络理论来对流行病传染现象进行分析的方法。传染病模型框架主要基于两个假设：可划分性和均匀混合性。可划分性是指传染病模型按照个体所处阶段对其进行分类，并且个体可以在不同阶段之间转化。均匀混合性是指可以认为任何人都可以感染其他任何人[36]，而不需要确切地知道疾病传播所依赖的接触网。传染病模型可以应用于不同学科领域的场景，分析不同类型系统的故障传播特征，对系统的脆弱性进行研究[37]。通过传染病模型研究发现，在故障动态传播过程中，网络的拓扑结构是很大的影响因素。例如在疾病传播过程中，个体主动与已感染个体彻底断开联系[38-39]，网络拓扑结构因此变化，进而会产生磁滞等丰富的动力学现象。

级联失效是指初始一小部分单元的故障有可能引发其他单元故障，进而产生连锁反应，最终导致网络无法履行正常功能[40]。因此级联失效模型可用于研究少数单元的故障是否会触发整个系统的故障等问题。级联失效模型大致可分为基于负载重新分配、基于节点相互依赖关系和基于邻居生存数量等三大类[41]。

在基于负载重新分配的级联失效模型中，每個单元有相应的容量并承担一定的负载。当某单元故障时，其所承担的负载会重新分配给其他单元。重新分配后，其他单元节点的负载可能超出容量，然后出现新的故障，从而引起故障传播。最直接的一类假设是，故障节点的负载会传播给邻居节点，如纤维束模型（fiber bundle model） [42]、沙堆模型[43-44]等。研究者围绕这些模型分析了网络的脆弱度如何随网络结构异质性等因素而改变。此外，在输送物质、能量、信息的基础设施网络中，流量重配策略并不只是简单地分配给邻居[45]。2002年Motter等[46]提出的级联失效模型则假定每对节点之间的流量（如因特网中的数据流量、交通系统中的车辆流量）按照最短路径分配，每个节点的负载是该节点的介数（通过该节点的最短路径数量），容量是初始负载的1+α倍，其中α为大于0的容忍（tolerance）参数。该模型表明，对于该类流量为负载的异质网络，级联失效机制也会引发类似于只攻击关键节点而造成整个系统崩溃的现象。

在基于节点相互依赖关系的级联失效模型中，节点与节点之间存在依赖关系，某个节点故障会引发依赖于该节点的相关节点发生故障。例如，互联网依赖于电力网络供电，电力网络依赖于互联网进行控制，电力网与互联网形成了相互耦合的网络。电力网络中的节点失效，将会导致依赖该节点的互联网中的节点失效，进而引发依赖于这些互联网节点的电力网络节点失效，故障不断传播导致系统崩溃。对该耦合网络模型[47]的研究发现，耦合关系较强时会产生不连续的渗流相变，即最大连通子团规模随着删去节点比例的增加而不连续地跳变为0。这对于系统风险的预测、管理是十分不利的。Parshani 等[48]提出了一个分析框架，用于研究同时包括连接关系连边和依赖关系连边的网络的稳健性。研究表明连接关系连边的故障和依赖关系连边之间存在协同作用，并引发了级联故障的迭代过程，对网络稳健性产生破坏性影响。Li等[49]建立了空间嵌入的相互依赖网络模型，并发现首次故障的范围超过阈值半径时就可能导致全局崩溃。上述负载重新分配的级联失效模型也可以建模为节点间相互依赖关系[50]。

在基于邻居存活数量的级联失效模型中，当节点邻居存活数量小于给定阈值时节点故障。这一类模型包括阈值模型（threshold model）[51]、k-core渗流[52]以及Bootstrap渗流[53]等模型。阈值模型中，每个节点故障当且仅当邻居故障的比例超过该节点的阈值，从而初始故障节点可能触发整个系统的崩溃。k-core渗流过程中，度小于k的节点会被移除，移除节点可能带来其他节点的度也小于k，从而引发级联失效的现象。k-core渗流能够区分出核心节点与边缘节点，可用于分析网络结构、识别脆弱节点[54]。Bootstrap渗流模型中，初始激活f比例的节点，其他节点若有k个邻居激活则也会被激活，从而产生级联现象。此外，除了基于故障传播模型之外，随着人工智能的发展，神经网络、图学习等方法也逐渐用于研究故障传播[55]。

1.3 基于故障传播模型的可靠性研究

上述故障机理揭示了复杂系统故障的传播规律，为分析和降低系统脆弱性提供有力的理论支持。目前研究者们基于故障传播模型展开了对系统可靠性方法的研究，包括对复杂系统的可靠性设计、可靠性评估、关键节点识别等。

在复杂系统可靠性设计方面，Adilson等[56]提出了一种基于在初始攻击后选择性地进一步移除部分节点和连边的无成本防御策略，通过移除部分单元阻断了故障级联传播，提高系统的可靠性。Yingrui等[57] 研究了相互依赖网络的负载重分配策略。相互依赖网络中，故障连边的一部分负载会通过耦合关系转移给相互依赖的另一个网络上。该研究提出了通过恰当选择网络耦合强度（一个网络中分配给其他网络的负载比例）可以增加两个网络生存的可能性。Christian等[58]提出了通过正确选择一小部分节点进行自治（独立于网络其他部分）可以显著提高鲁棒性。研究发现介数和度是选择此类节点的关键参数，通过保护介数最高的少数节点可显著降低系统崩溃的可能性。Schfer等[59]提出了在故障发生时重新分配负载的策略。该策略中基于最短流路径的策略能够将之前的异构负载分布的网络节点和链路变为更加均匀的负载分布。这些流路径的使用能够增加网络的鲁棒性，同时减少网络容量布局的投入成本。Pastor-Satorras等[60]提出了依赖于网络特定无标度结构的最佳免疫策略，为避免故障传播并提高系统鲁棒性提供了理论分析。

在复杂系统可靠性评估方面，Li等[31]对交通流网络进行渗流分析，发现在渗流阈值附近交通系统的连通状态会从全局连通变为局部连通，为控制系统拥堵提供了有效帮助。此外，Li等[50]发现因局部故障引发的故障呈现辐射状以近似常速进行传播，通过理论分析给出故障传播速度则随着单元对故障的容忍程度的升高而降低，并在大量网络中得到了验证。Zeng等[61]基于渗流理论对故障模式进行研究，提出了涵盖交通拥堵从出现、演化到消散整个生命周期的健康管理框架，为未来交通的智能管理提供了理论支撑。

在识别关键节点方面，Yang等[62]提出了一个动态级联失效模型，模拟了电网系统中的级联故障。研究基于该模型识别出了电网的关键脆弱节点并发现给定电网中的相同扰动会在不同条件下导致不同的结果，即从没有损坏到大规模级联。Nesti等[63]构建了故障传播模型，对电网的故障模式进行识别，根据故障的可能性对线路故障模式进行排序，并确定了此类电网最可能的故障发生方式和故障传播方式。Liu等[64]利用小世界网络理论分析了系统的拓扑结构统计特性，提出了基于小世界聚类的故障传播模型，并利用Dijkstra算法找到了具有高扩散能力的故障传播路径和相关关键节点，验证了该方法能够有效地发现系统的薄弱点，为设计改进和故障预防提供重要依据。

2 考虑故障恢复的系统适应性研究

适应性是指系统在不断变化的环境中仍然保持自身性能的能力。系统适应性使系统能从压力中恢复[65]，反映系统适应性的两个关键因素分别是系统降级程度和系统性能恢复时间[66]。图2展示了系统性能在扰动前后的变化[67]。te时刻系统受到扰动，td时刻系统受扰结束，系统性能水平由F（t0） 降至F（td）。ts时刻系统开始恢复性能，tf时刻系统到达最终平衡状态，系统性能水平恢复至F（tf）。

2.1 复杂系统适应性的景观理论

复杂系统对扰动的适应过程可用动力系统理论进行建模。动力系统理论中，系统由一组状态变量所刻画，系统状态变量的各个分量联合定义了系统是否健康可靠。一个处在健康状态的复杂系统，在扰动下可能会突然进入故障状态，例如生态系统的物种灭绝[65]、热带雨林的沙地化[68]、金融危机[69]等等。系统状态变量的演化规律由微分方程或随机微分方程所描述，系统的稳定状态就是微分方程的吸引子[70]，系统内可能存在多个吸引子。外界对一个复杂系统的状态变量x或者系统参数θ进行扰动，系统因适应性不会直接脱离现有吸引子状态，依旧维持稳定。但当扰动足够大，超过系统恢复能力的临界点，使系统无法适应该变化时，系统可能脱离原有的吸引子状态，被其他吸引子吸引。

由于微分方程或隨机微分方程常常可由能量景观所表示，复杂系统扰动前后的适应过程可以用景观进行直观描述[71]（如图3所示）。系统可以看作景观曲面上运动的小球，景观高度表示系统的能量（Lyapunov函数值），小球倾向于往系统能量低的状态运动，即小球会倾向于向谷底运动。如图3（a）所示该景观有两个“谷底”，每个“谷底”表示一个吸引子。对处于健康态的系统施加扰动，系统状态发生改变，对应于图中实心小球的移动。小扰动下系统状态不会脱离健康态吸引子。大扰动下系统则会脱离健康态吸引子，进入故障态。对系统参数θ的扰动，对应于图中三维景观形状的改变（如图3（b）所示）。当系统参数改变到临界点时，健康态失稳，系统发生故障。而当系统健康态对应的吸引域越大、越深时，系统越容易在扰动后保持在健康态。

在处理由少数变量描述的低维系统时，只需沿用经典的动力系统理论即可。但当处理由高维状态变量描述的系统时，例如大量基因组成的调控网络或由大量物种组成的生态系统，就会面临状态空间指数爆炸、系统参数多等困难。对于此类高维系统，可结合统计物理中的粗粒化、平均场近似等技术来克服局限性[72-73]。近年来，自旋玻璃理论被引入用于分析生态系统的稳态性质[74]。例如Altieri 等[75]使用自旋玻璃中的Replica方法对广义L-V方程进行求解，发现了低噪音下存在玻璃相，系统吸引子的个数正比于变量数的指数倍。Gao等[76]对包括基因、化学反应等多种类型网络动力学进行粗粒化得到了系统崩溃的临界点。

2.2 基于景观理论的系统适应性分析

景观理论能够衡量系统是否即将发生故障或者崩溃，并揭示复杂系统崩溃的根源，为分析系统适应性提供支持，被广泛应用于不同领域。例如在生物领域， Huang等[77]发现了癌症等疾病可以理解为基因调控网络动力学中的吸引子。这种吸引子可能是正常细胞中本就具备的，也可能是基因突变后产生的。在生态领域，Hoegh-Guldberg等[78]分析了珊瑚礁的恢复能力，识别了珊瑚生长速率（系统参数）的临界点。当珊瑚生长速率下降到临界点，原本由珊瑚主导的生态环境将突变为水藻主导的生态环境。在社会科学领域，极端思想的传播在互联网属于一种故障态对应的吸引子。Johnson等[79]建立了网络极端思想的模型，指出了由于极端思想网络的适应性，单个平台大幅度封杀并不足以使极端思想在互联网上灭绝，反而可能加剧极端思想的发展。

将复杂系统的崩溃或者故障建模为健康状态吸引子的失稳，也可以指导不同领域复杂系统可靠性设计和诊断。在复杂系统可靠性设计方面，研究发现元素间存在强耦合的系统容易存在临界点，减少耦合可避免系统发生突变[40]。随着复杂系统单元之间的交互变强，系统单元的行为可能会严重改变或损害其他单元的功能或操作。因为强耦合系统的动态变化往往很快，可能超过人类反应的速度。金融危机就是强耦合导致系统崩溃的事例。因此为了使系统具有更高的可靠性，需要适当降低系统中的耦合强度。在可靠性诊断方面，有研究利用临界点附近存在临界慢化[80]以及闪烁（flickerling）[81]等现象实现对系统状态（是否达到临界点）的预测[82]。例如，Veraart等[83]构建了蓝藻微观世界来测试临界慢化现象，蓝藻微观世界受到扰动的实验表明，临界慢化确实发生，恢复速度可用于衡量复杂系统的恢复能力，预测系统到临界状态的距离，从而判断系统是否即将崩溃。

3 讨论与结论

可靠性学科是一门与故障做斗争的学科，复杂系统可靠性的研究主要围绕故障展开。故障有两种演化方向：故障扩散与故障恢复。研究从这两个角度出发，一是考虑故障传播的系统脆弱性研究；二是考虑故障恢复的系统适应性研究。系统脆弱性研究的重点在于挖掘系统崩溃的内在机理，即故障的传播机理。系统适应性研究的重点在于基于動力系统与景观理论挖掘系统故障恢复机理，包括分析系统故障恢复的临界点。基于故障传播[31，50]和故障恢复机理[84-86]，提出了一系列复杂系统可靠性技术，从而实现对复杂系统的评估、诊断、调控[87-89]。

伴随着全球化以及信息技术的发展，交通系统、电力系统、金融系统等系统必将越发复杂，系统内单元数量以及关联程度都将大大增加。单元间的相互依赖可能使少数单元的故障引发整个系统的级联失效，单元间的复杂相互作用也可能产生未知的故障态吸引子，产生负向涌现。因此，构建、维护复杂系统必将面临可靠性的挑战。在过度耦合带来风险的同时，也可以利用系统的复杂性来增强系统的可靠性。如何通过在系统内恰当地引入复杂性（单元之间恰当的组织形式）以赋予系统自我恢复能力，将是未来构建高可靠复杂系统的关键[90]。

参考文献：

［1］于景元. 钱学森系统科学思想和系统科学体系[J]. 科学决策， 2014（12）： 1-22. DOI： 10.3773/j.issn.1006-4885.2014.12.002.

[2]GALLAGHER R， APPENZELLER T. Beyond reductionism[J]. Science， 1999， 284（5411）： 79. DOI： 10.1126/science.284.5411.79.

[3]钱学森， 于景元， 戴汝为. 一个科学新领域：开放的复杂巨系统及其方法论[J]. 自然杂志， 1990， 12（1）： 3-10.

[4]钱学森．创建系统学[M]．太原： 山西科学技术出版社， 2001：11.

[5]郭雷. 系统科学进展[M]. 北京： 科学出版社， 2017.

[6]方福康. 神经系统中的复杂性研究[J]. 上海理工大学学报， 2011， 33（2）： 103-110. DOI： 10.13255/j.cnki.jusst.2011.02.006.

[7]方福康， 袁强. 经济增长的复杂性与 “J” 结构[J]. 系统工程理论与实践， 2002， 22（10）： 12-20. DOI： 10.3321/j.issn： 1000-6788.2002.10.003.

[8]王众托.知识系统工程与现代科学技术体系[J]. 上海理工大学学报， 2011， 33（6）： 613-630. DOI： 10.13255/j.cnki.jusst.2011.06.007.

[9]彭张林，张强，杨善林.综合评价理论与方法研究综述[J].中国管理科学，2015，23（S1）：245-256.

[10][ZK（#]陈光亚. 向量优化问题某些基础理论及其发展[J]. 重庆师范大学学报（自然科学版）， 2005， 22（3）： 6-9. DOI： 10.3969/j.issn.1672-6693.2005.03.002.

[11]狄增如.探索复杂性是发展系统学的重要途径[J].系统工程理论与实践，2011，31（S1）：37-42.

[12]吴俊， 邓宏钟， 谭跃进. 基于自然连通度的随机网络抗毁性研究[C]// 第五届全国复杂网络学术会议论文（摘要）汇集. 青岛：中国工业与应用数学学会， 2009： 100.

[13]盛昭瀚， 张维. 管理科学研究中的计算实验方法[J]. 管理科学学报， 2011， 14（5）： 1-10.

[14]徐玖平， 卢毅. 地震灾后重建系统工程的综合集成模式[J]. 系统工程理论与实践， 2008， 28（7）： 1-16. DOI： 10.3321/j.issn： 1000-6788.2008.07.001.

[15]赵庆祯， 王文宾， 赵培忻. 农业物流绩效评价的ANP方法[J]. 农业系统科学与综合研究， 2005， 21（3）： 237-240.

[16]陈锡康， 杨翠红. 农业复杂巨系统的特点与全国粮食产量预测研究[J]. 系统工程理论与实践， 2002， 22（6）： 108-112. DOI： 10.3321/j.issn： 1000-6788.2002.06.019.

[17]高自友， 赵小梅， 黄海军等. 复杂网络理论与城市交通系统复杂性问题的相关研究[J]. 交通运输系统工程与信息， 2006， 6（3）： 41-47. DOI： 10.16097/j.cnki.1009-6744.2006.03.007.

[18]黄海军. 城市交通网络平衡分析： 理论与实践[M]. 北京： 人民交通出版社， 1994.

[19]顾基发， 唐锡晋， 朱正祥. 物理-事理-人理系统方法论综述[J]. 交通运输系统工程与信息， 2007， 7（6）： 51-60. DOI： 10.16097/j.cnki.1009-6744.2007.06.001.

[20]邓聚龙. 灰色系统综述[J]. 世界科学， 1983（7）： 1-5.

[21]汪寿阳， 余乐安， 黎建强. TEI@I方法论及其在外汇汇率预测中的应用[J]. 管理学报， 2007， 4（1）： 21-27. DOI： 10.3969/j.issn.1672-884X.2007.01.004.

[22]TAIT N. Robert lusser and lussers law[J]. Safety and Reliability， 1995， 15（2）： 15-18. DOI： 10.1080/09617353.1995.11690648.

[23]von NEUMANN J. Probabilistic logics and the synthesis of reliable organisms from unreliable components[M]//Automata Studies. （AM-34）. Princeton： Princeton University Press， 1956： 43-98. DOI： 10.1515/9781400882618-003.

[24]楊为民， 阮镰， 屠庆慈. 可靠性系统工程：理论与实践[J]. 航空学报， 1995 （S1）： 1-8.

[25]康锐， 王自力. 可靠性系统工程的理论与技术框架[J]. 航空学报， 2005， 26（5）： 633-636. DOI： 10.3321/j.issn： 1000-6893.2005.05.018.

[26]DONALDSON-MATASCI M C， LACHMANN M， BERGSTROM C T. Phenotypic diversity as an adaptation to environmental uncertainty[J]. Evolutionary Ecology Research， 2008， 10（4）： 493-515.

[27]REY K， AMIOT R， FOUREL F， et al. Oxygen isotopes suggest elevated thermometabolism within multiple Permo-Triassic therapsid clades[J]. eLife， 2017， 6： e28589. DOI： 10.7554/eLife.28589.

[28]BASCOMPTE J， JORDANO P， MELIN C J， et al. The nested assembly of plant-animal mutualistic networks[J]. Proceedings of the National Academy of Sciences of the United States of America， 2003， 100（16）： 9383-9387. DOI： 10.1073/pnas.1633576100.

[29]HAVLIN S， BUNDE A. 3. percolation[M]//Contemporary Problems in Statistical Physics. Philadelphia： Society for Industrial and Applied Mathematics， 1994： 103-146. DOI： 10.1137/1.9781611971552.ch3.

[30]STAUFFER D， AHARONY A. Introduction to percolation theory[M]. London： Taylor & Francis， 2018. DOI： 10.1201/9781315274386.

[31]LI D Q， FU B W， WANG Y P， et al. Percolation transition in dynamical traffic network with evolving critical bottlenecks[J]. Proceedings of the National Academy of Sciences of the United States of America， 2015， 112（3）： 669-672. DOI： 10.1073/pnas.1419185112.

[32]ALBERT R， JEONG H， BARABSI A L. Error and attack tolerance of complex networks[J]. Nature， 2000， 406： 378-382. DOI： 10.1038/35019019.

[33]BARABSI A L. Scale-free networks： a decade and beyond[J]. Science， 2009， 325（5939）： 412-413. DOI： 10.1126/science.1173299.

[34]COHEN R， EREZ K， BEN-AVRAHAM D， et al. Resilience of the Internet to random breakdowns[J]. Physical Review Letters， 2000， 85（21）： 4626-4628. DOI： 10.1103/PhysRevLett.85.4626.

[35]HOLME P， KIM B J， YOON C N， et al. Attack vulnerability of complex networks[J]. Physical Review E， 2002， 65（5）： 056109. DOI： 10.1103/physreve.65.056109.

[36]ANDERSON R M， MAY R M. Infectious diseases of humans dynamics and control[M]. Oxford： Oxford University Press， 1991.

[37]PASTOR-SATORRAS R， CASTELLANO C， van MIEGHEM P， et al. Epidemic processes in complex networks[EB/OL]. （2014-08-12）［2024-02-01］. http：//arxiv.org/abs/1408.2701

[38]GROSS T， DOMMAR DLIMA C J， BLASIUS B. Epidemic dynamics on an adaptive network[J]. Physical Review Letters， 2006， 96（20）： 208701. DOI： 10.1103/PhysRevLett.96.208701.

[39]QIU Z R， ESPINOZA B， VASCONCELOS V V， et al. Understanding the coevolution of mask wearing and epidemics： a network perspective[J]. Proceedings of the National Academy of Sciences of the United States of America， 2022， 119（26）： e2123355119. DOI： 10.1073/pnas.2123355119.

[40]HELBING D. Globally networked risks and how to respond[J]. Nature， 2013， 497： 51-59. DOI： 10.1038/nature12047.

[41]VALDEZ L D， SHEKHTMAN L， LA ROCCA C E， et al. Cascading failures in complex networks[J]. Journal of Complex Networks， 2020， 8（2）： cnaa013. DOI： 10.1093/comnet/cnaa013.

[42]MORENO Y， GMEZ J B， PACHECO A F. Instability of scale-free networks under node-breaking avalanches[J]. Europhysics Letters， 2002， 58（4）： 630-636. DOI： 10.1209/epl/i2002-00442-2.

[43]GOH K I， LEE D S， KAHNG B， et al. Sandpile on scale-free networks[J]. Physical Review Letters， 2003， 91（14）： 148701. DOI： 10.1103/PhysRevLett.91.148701.

[44]GAI P， KAPADIA S. Contagion in financial networks[J]. Proceedings of the Royal Society A： Mathematical， Physical and Engineering Sciences， 2010， 466（2120）： 2401-2423. DOI： 10.1098/rspa.2009.0410.

[45]WANG W X， CHEN G R. Universal robustness characteristic of weighted networks against cascading failure[J]. Physical Review E， Statistical， Nonlinear， and Soft Matter Physics， 2008， 77（2）： 026101. DOI： 10.1103/PhysRevE.77.026101.

[46]MOTTER A E， LAI Y C. Cascade-based attacks on complex networks[J]. Physical Review E， 2002， 66（6）： 065102. DOI： 10.1103/physreve.66.065102.

[47]BULDYREV S V， PARSHANI R， PAUL G， et al. Catastrophic cascade of failures in interdependent networks[J]. Nature， 2010， 464： 1025-1028. DOI： 10.1038/nature08932.

[48]PARSHANI R， BULDYREV S V， HAVLIN S. Critical effect of dependency groups on the function of networks[J]. Proceedings of the National Academy of Sciences of the United States of America， 2011， 108（3）： 1007-1010. DOI： 10.1073/pnas.1008404108.

[49]LI W， BASHAN A， BULDYREV S V， et al. Cascading failures in interdependent lattice networks： the critical role of the length of dependency links[J]. Physical Review Letters， 2012， 108（22）： 228702. DOI： 10.1103/PhysRevLett.108.228702.

[50]ZHAO J C， LI D Q， SANHEDRAI H， et al. Spatio-temporal propagation of cascading overload failures in spatially embedded networks[J]. Nature Communications， 2016， 7： 10094. DOI： 10.1038/ncomms10094.

[51]WATTS D J. A simple model of global cascades on random networks[J]. Proceedings of the National Academy of Sciences of the United States of America， 2002， 99（9）： 5766-5771. DOI： 10.1073/pnas.082090499.

[52]DOROGOVTSEV S N， GOLTSEV A V， MENDES J F F. K-Core organization of complex networks[J]. Physical Review Letters， 2006， 96（4）： 040601. DOI： 10.1103/PhysRevLett.96.040601.

[53]BAXTER G J， DOROGOVTSEV S N， GOLTSEV A V， et al. Bootstrap percolation on complex networks[J]. Physical Review E， Statistical， Nonlinear， and Soft Matter Physics， 2010， 82（1）： 011103. DOI： 10.1103/PhysRevE.82.011103.

[54]LEE D， JO M， KAHNG B. Critical behavior of k-core percolation： Numerical studies[J]. Physical Review E， 2016， 94（6）： 062307. DOI： 10.1103/PhysRevE.94.062307.

[55]GRASSIA M， DE DOMENICO M， MANGIONI G. Machine learning dismantling and early-warning signals of disintegration in complex systems[J]. Nature Communications， 2021， 12： 5190. DOI： 10.1038/s41467-021-25485-8.

[56]MOTTER A E. Cascade control and defense in complex networks[J]. Physical Review Letters， 2004， 93（9）： 098701. DOI： 10.1103/PhysRevLett.93.098701.

[57]ZHANG Y R， ARENAS A， YAGAN O. Cascading failures in interdependent systems under a flow redistribution model[J]. Physical Review E， 2018， 97（2）： 022307. DOI： 10.1103/PhysRevE.97.022307.

[58]SCHNEIDER C M， YAZDANI N， ARAJO N A M， et al. Towards designing robust coupled networks[J]. Scientific Reports， 2013， 3： 1969. DOI： 10.1038/srep01969.

[59]SCHFER M， SCHOLZ J， GREINER M. Proactive robustness control of heterogeneously loaded networks[J]. Physical Review Letters， 2006， 96（10）： 108701. DOI： 10.1103/PhysRevLett.96.108701.

[60]PASTOR-SATORRAS R， VESPIGNANI A. Immunization of complex networks[J]. Physical Review E， 2002， 65（3）： 036104. DOI： 10.1103/physreve.65.036104.

[61]ZENG G W， SUN Z Y， LIU S Y， et al. Percolation-based health management of complex traffic systems[J]. Frontiers of Engineering Management， 2021， 8（4）： 557-571. DOI： 10.1007/s42524-021-0174-0.

[62]YANG Y， NISHIKAWA T， MOTTER A E. Small vulnerable sets determine large network cascades in power grids[J]. Science， 2017， 358（6365）： eaan3184. DOI： 10.1126/science.aan3184.

[63]NESTI T， ZOCCA A， ZWART B. Emergent failures and cascades in power grids： a statistical physics perspective[J]. Physical Review Letters， 2018， 120（25）： 258301. DOI： 10.1103/PhysRevLett.120.258301.

[64]LIU X F， AN S Q. Failure propagation analysis of aircraft engine system based on the small-world net model[C]//Proceedings of the 32nd Chinese Control Conference. Xian， China：IEEE， 2013： 1214-1219.

[65]HOLLING C S. Resilience and stability of ecological systems[J]. Annual Review of Ecology and Systematics， 1973， 4： 1-23. DOI： 10.1146/annurev.es.04.110173.000245.

[66]ZOBEL C W. Representing perceived tradeoffs in defining disaster resilience[J]. Decision Support Systems， 2011， 50（2）： 394-403. DOI： 10.1016/j.dss.2010.10.001.

[67]HENRY D， EMMANUEL RAMIREZ-MARQUEZ J. Generic metrics and quantitative approaches for system resilience as a function of time[J]. Reliability Engineering & System Safety， 2012， 99： 114-122. DOI： 10.1016/j.ress.2011.09.002.

[68]HIROTA M， HOLMGREN M， VAN NES E H， et al. Global resilience of tropical forest and savanna to critical transitions[J]. Science， 2011， 334（6053）： 232-235. DOI： 10.1126/science.1210657.

[69]HALDANE A G， MAY R M. Systemic risk in banking ecosystems[J]. Nature， 2011， 469： 351-355. DOI： 10.1038/nature09659.

[70]STROGATZ S H. Nonlinear dynamics and chaos with student solutions manual： with applications to physics， biology， chemistry， and engineering[M]. Second edition. Florida： CRC Press， 2018. DOI： 10.1201/9780429399640.

[71]WALKER B， HOLLING C S， CARPENTER S R， et al. Resilience， adaptability and transformability in social-ecological systems[J]. Ecology and Society， 2004， 9（2）： 5. DOI： 10.5751/es-00650-090205.

[72]VOLO M D， ROMAGNONI A， CAPONE C， et al. Biologically realistic mean-field models of conductance-based networks of spiking neurons with adaptation[J]. Neural Computation， 2019， 31（4）： 653-680. DOI： 10.1162/neco_a_01173.

[73]FERET J， DANOS V， KRIVINE J， et al. Internal coarse-graining of molecular systems[J]. Proceedings of the National Academy of Sciences of the United States of America， 2009， 106（16）： 6453-6458. DOI： 10.1073/pnas.0809908106.

[74]CUI W P， MARSLAND R， MEHTA P. Effect of resource dynamics on species packing in diverse ecosystems[J]. Physical Review Letters， 2020， 125（4）： 048101. DOI： 10.1103/PhysRevLett.125.048101.

[75]ALTIERI A， ROY F， CAMMAROTA C， et al. Properties of equilibria and glassy phases of the random lotka-volterra model with demographic noise[J]. Physical Review Letters， 2021， 126（25）： 258301. DOI： 10.1103/PhysRevLett.126.258301.

[76]GAO J X， BARZEL B， BARABSI A L. Universal resilience patterns in complex networks[J]. Nature， 2016， 530： 307-312. DOI： 10.1038/nature16948.

[77]HUANG S， ERNBERG I， KAUFFMAN S. Cancer attractors： a systems view of tumors from a gene network dynamics and developmental perspective[J]. Seminars in Cell & Developmental Biology， 2009， 20（7）： 869-876. DOI： 10.1016/j.semcdb.2009.07.003.

[78]HOEGH-GULDBERG O， MUMBY P J， HOOTEN A J， et al. Coral reefs under rapid climate change and ocean acidification[J]. Science， 2007， 318（5857）： 1737-1742. DOI： 10.1126/science.1152509.

[79]JOHNSON N F， LEAHY R， RESTREPO N J， et al. Hidden resilience and adaptive dynamics of the global online hate ecology[J]. Nature， 2019， 573： 261-265. DOI： 10.1038/s41586-019-1494-7.

[80]WISSEL C. A universal law of the characteristic return time near thresholds[J]. Oecologia， 1984， 65（1）： 101-107. DOI： 10.1007/BF00384470.

[81]DAKOS V， VAN NES E H， SCHEFFER M. Flickering as an early warning signal[J]. Theoretical Ecology， 2013， 6（3）： 309-317. DOI： 10.1007/s12080-013-0186-4.

[82]SCHEFFER M， CARPENTER S R， LENTON T M， et al. Anticipating critical transitions[J]. Science， 2012， 338（6105）： 344-348. DOI： 10.1126/science.1225244.

[83]VERAART A J， FAASSEN E J， DAKOS V， et al. Recovery rates reflect distance to a tipping point in a living system[J]. Nature， 2012， 481： 357-359. DOI： 10.1038/nature10723.

[84]GAO S L， LI D Q， ZHENG N， et al. Resilient perimeter control for hyper-congested two-region networks with MFD dynamics[J]. Transportation Research Part B： Methodological， 2022（156）： 50-75.

[85]LIU T， GUO S， LIU H， et al. Network resilience in the aging brain[EB/OL]. （2022-02-03）［2024-02-01］.  http：//arxiv.org/abs/2202.01516.

[86]ZHANG L M， ZENG G W， LI D Q， et al. Scale-free resilience of real traffic Jams[J]. Proceedings of the National Academy of Sciences of the United States of America， 2019， 116（18）： 8673-8678. DOI： 10.1073/pnas.1814982116.

[87]ZENG G W， GAO J X， SHEKHTMAN L， et al. Multiple metastable network states in urban traffic[J]. Proceedings of the National Academy of Sciences of the United States of America， 2020， 117（30）： 17528-17534. DOI： 10.1073/pnas.1907493117.

[88]ZHONG J L， SANHEDRAI H， ZHANG F M， et al. Network endurance against cascading overload failure[J]. Reliability Engineering & System Safety， 2020， 201： 106916. DOI10.1016/j.ress.2020.106916.

[89]HAMEDMOGHADAM H， ZHENG N， LI D Q， et al. Percolation-based dynamic perimeter control for mitigating congestion propagation in urban road networks[J]. Transportation Research Part C： Emerging Technologies， 2022， 145： 103922. DOI： 10.1016/j.trc.2022.103922.

[90]LIU X M， LI D Q， MA M Q， et al. Network resilience[J]. Physics Reports， 2022， 971： 1-108. DOI： 10.1016/j.physrep.2022.04.002.