地铁乘客的病毒载量演化模型和仿真

卢守峰 黄志康 赵红云

摘要：为了微观刻画地铁乘客的病毒传播，构建了吸入病毒概率与社交距离之间的函数关系，建立了病毒载量增加量和减少量的计算公式，在此基础上建立了病毒载量演化方程，其中防疫措施的效果以归一化的参数描述。通过Anylogic软件的二次开发接口，对每个乘客的病毒载量进行编程，刻画每个乘客在感染前和感染后两个阶段的病毒载量变化。仿真初始时刻设定10%的乘客被病毒感染，包括普通感染者和超级感染者。对不同乘客数量条件下的病毒演化进行仿真，分为有管控和无管控两种场景。仿真结果表明：随着乘车人数的增多，乘客密度增大，病毒传播增强，个体病毒载量增加较快；对病毒载量大于1 000的乘客进行管控，禁止其乘车，可将所有乘客的病毒载量降低一个数量级。

关键词：城市交通；地铁乘客；病毒载量；疫情管控；演化模型；Anylogic仿真

中图分类号：U12; R181.8   文献标志码：A   文章编号：1002-4026（2024）02-0097-07

The evolution model and simulation of the viral load of subway passengers

Abstract∶A functional relationship was constructed between the probability of inhaling viruses and social distance to characterize the viral transmission of subway passengers at the microscopic level. Formulas for calculating the increase and decrease of viral load were constructed based on establishing the viral load evolution equation. Normalized parameters were used within this equation to describe the effect of pandemic prevention measures. The viral load of each passenger was programmed through the Anylogic softwares secondary development interface to characterize the viral load change at the pre- and post-infection phases. In the initial simulation settings， 10% of the passengers were infected with the virus， including ordinary carriers and supercarriers. The evolution of the virus under different passenger number conditions within subway carriages was simulated， which was categorized into with-control and without-control scenarios. The simulation results showed the following： as the number of passengers increases， the passenger density increases， the virus transmission increases， and the individual viral load increases rapidly. Isolating passengers with a viral load greater than a threshold of 1 000 and prohibiting them from taking the subway can reduce the viral load of all passengers by an order of magnitude.

Key words∶urban transportation; subway passengers; viral load; pandemic control; evolutionary model; Anylogic simulation

新型冠狀病毒的传播方式、检测方法、管控模式、相关配套措施具有典型代表性，研究新型冠状病毒感染的精细化管控措施对于其他呼吸道病毒管控有着重要的借鉴意义。我国学者一直关注各种场景下的新型冠状病毒的传播规律和管控策略。例如李小莉等[1]构建了考虑传染概率的政府部门与公众演化博弈模型，研究了不同传染概率下政府防疫管控策略的演化。方丹辉等[2]提出了一种考虑高低防护人群且将感染者归入移出者的易感者-暴露者-康复者传染病模型（susceptible-exposed-recovered， SER），研究了不同等级管控措施的效果。马剑等[3]构建了校园内上下课行人流模型，通过时空伴随概念量化行人接触导致的疫情传播风险，利用Anylogic软件对不同的校园疫情防控策略效果进行仿真。

已有关于公共交通内疫情传播模型主要以易感者-感染者-康复者（susceptible-infective-recovered， SIR）模型、Wells-Riley模型为主。SIR模型描述各类个体（易感者、感染者、康复者）的数量随时间的变化，适合宏观上描述大范围内的疫情传播。近期相关文献利用该模型对公共交通防疫措施的有效性进行了研究。例如施红生[4]对铁路交通的传染病防控模式进行评估，通过对SARS、甲型H1N1流感等防控案例分析，提出了远距离铁路交通传染病传播数学模型，表明在长距离铁路交通环境下提前进行病毒检测、乘务人员的免疫率达到50%可以有效减少病毒传播。贾兴利等[5]在SIR模型基础上，考虑了病毒的潜伏期、人口迁徙、市内小区人口流动等因素建立了市域新型冠状病毒疫情传播模型，对比分析了4个城市交通管控措施对于疫情发展的阻断效果，结果表明及时全面地实施市内道路封闭、客运交通停运和小区人口流动控制三种交通管控措施可以有效阻断疫情传播、控制市域疫情发展。

Wells-Riley模型计算每个个体感染病毒的概率，输入变量是宏观变量。近期相关文献从防疫措施、病毒传播过程两个方面对该模型进行了改进，更好地描述公共交通内疫情传播。例如，陈国强等[6]在Wells-Riley传染病模型基础上，考虑乘客个体差异、飞沫传播距离、口罩保护率、疫苗免疫情况及车厢消毒等影响因素，建立符合公交车辆运行环境的多智能体新型冠状病毒传播模型，结果表明车辆及时进行消毒、提高乘客提高口罩的佩戴率疫苗接种率能有效减少新型冠状病毒传播。Sun等[7]在原有Wells-Riley方程基础上添加社交距离、环境通风量等影响因素，结果表明增加社交距离可以在30 min内显著降低20%～40%的感染率。Yan等[8]对飞沫在波音737客舱的传播过程进行研究，使用拉格朗日方程代替欧拉方程模拟飞沫传播特性，改进传统Wells-Riley方程。谢国等[9]利用高斯公式模拟病毒的传播过程，改进Wells-Riley方程，选取CRH2型动车组为模拟环境，提出了有利于降低新型冠状病毒传播概率的乘客座位分布模式。

以上文献对新型冠状病毒的传播和管控措施的有效性进行了研究，但是现有模型偏宏观，无法刻画个体的病毒载量随时间的变化，不能为精准管控提供理论依据。本文的研究目标是建立地铁车厢内个体病毒载量的演化模型，对是否被感染的状态进行预测，然后研究防控措施对病毒载量的影响，从而为主动精准管控提供理论依据。

1 病毒载量的演化模型

病毒载量演化的建模方法是物质守恒和随机建模。病毒载量代表的是病毒的负荷，即体内病毒的数量。通常新型冠状病毒的浓度越高，人被感染的可能性往往会更大，此外，病毒活性、自身免疫力等因素也是导致机体感染的重要因素。Ma等[10]研究表明人体呼吸是新型冠状病毒重要传播方式。Zhang等[11]研究表明空气传播是新型冠状病毒传播的主要途径，其传播率是接触传播的1 000倍。

基于以上研究结果，本研究主要考虑个体以呼吸方式传播和吸入病毒。个体内的病毒载量是动态变化的，其随时间的变化等于增加量减去减少量。病毒载量用w表示，其演化方程建模为

其中，w+是病毒载量的增加量，w-是病毒载量的减少量。

感染前，体内的病毒不会复制；感染后，体内病毒会复制。根据这一特点，建模区分为感染前和感染后两个阶段。

1.1 感染前阶段的病毒载量增加量

采用随机建模方法，建立了吸入病毒与社交距离之间的概率公式，吸入病毒的概率随着社交距离的增加而降低。如图1所示。

图1展示两个社交距离的阈值ｄｃ和ｄｍａｘ，当社交距离小于dc时，在无防护措施情况下，吸入相邻个体呼出的病毒的概率为1。当社交距离大于dmax时，吸入相邻个体呼出的病毒的概率为0。当介于两者之间时，吸入相邻个体呼出的病毒的概率呈线性衰减。在实际应用过程中，两个参数dc和dmax可使用实测数据标定。本文建立的目标个体吸入病毒的概率见公式（2）。

其中，P是吸入病毒的概率;x是研究的目标个体的位置;x* 是相邻个体的位置;H（·） 是赫维赛德函数， 当（·）≥０时Ｈ（·）=1，当（·）<０时Ｈ（·）=0。

设研究的目标个体在dmax为其半径的圆周范围内有n个相邻个体。n个相邻个体从t0时刻到当前时刻t，产生的对目标个体有所影响的病毒总量为

其中，qi为每个个体单位时间内产生的病毒数量;pi为目标个体吸入第i个相邻个体产生的病毒的概率；s为时间。

1.2 感染后阶段的病毒载量增加量

一个人感染新型冠状病毒后，病毒复制是病毒增长的主要原因。由于病毒复制带来的病毒数量远远大于吸入病毒的数量，因此感染后阶段只需要考虑病毒复制导致的病毒载量增加量。

1.3 病毒载量减少量

根据Popa等[13]的研究结果，一个人平均吸入1 000个病毒颗粒被感染。本文以该值作为阈值，当个体体内的病毒颗粒小于1 000个时，体内的病毒量将一直累加，不排出病毒。当个体体内的病毒颗粒超过1 000个时，该个体变为感染个体。感染个体的排毒量与体内的病毒数量有一定关系，本文假设感染者的排毒量等于个体体内病毒载量的0.1%。

其中，N表示个体内的病毒载量；w－表示呼出的病毒数量。

1.4 防疫措施的干预效果建模

在公共交通车辆上，采取的防疫措施主要包括戴口罩或面罩、增加社交距离、车厢消毒、通风。其中前两项措施是减少病毒的吸入量，后两项措施是减少病毒的数量。各类防疫措施的效果用参数α表示，取值范围是［0，1］，其中0表示完全阻挡病毒侵入，1表示防疫措施没有防护作用，中间值表示使用防疫措施后吸入病毒的概率。在公式（4）的基础上乘以参数α，描述防疫措施的干预效果。

2 基于Anylogic 仿真软件的管控措施效果评估

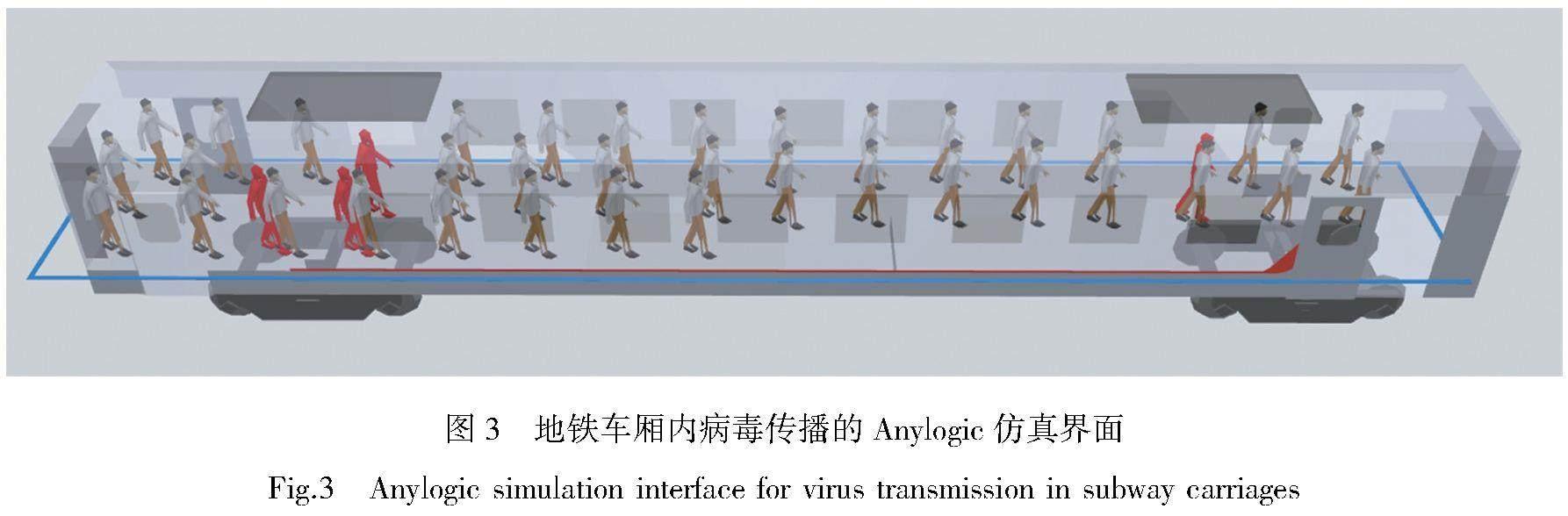
Anylogic仿真软件为行人智能体提供了二次开发的接口。本部分在二次开发接口中对公式（1）～（6）进行编程。首先在Anylogic软件中对地铁车厢建立物理模型；再使用Anylogic软件提供的逻辑流程图工具对乘客行为编程，包括进站乘客流线和出站乘客流线；然后设置客流量、乘客在地铁车厢中的间距等参数；利用Anylogic软件提供的二次开发接口，对本文建立的病毒载量演化模型进行编程；最后设置仿真时长，输出仿真数据。仿真界面如图3所示，红色乘客表示受感染的乘客，灰色乘客表示未受感染的乘客。

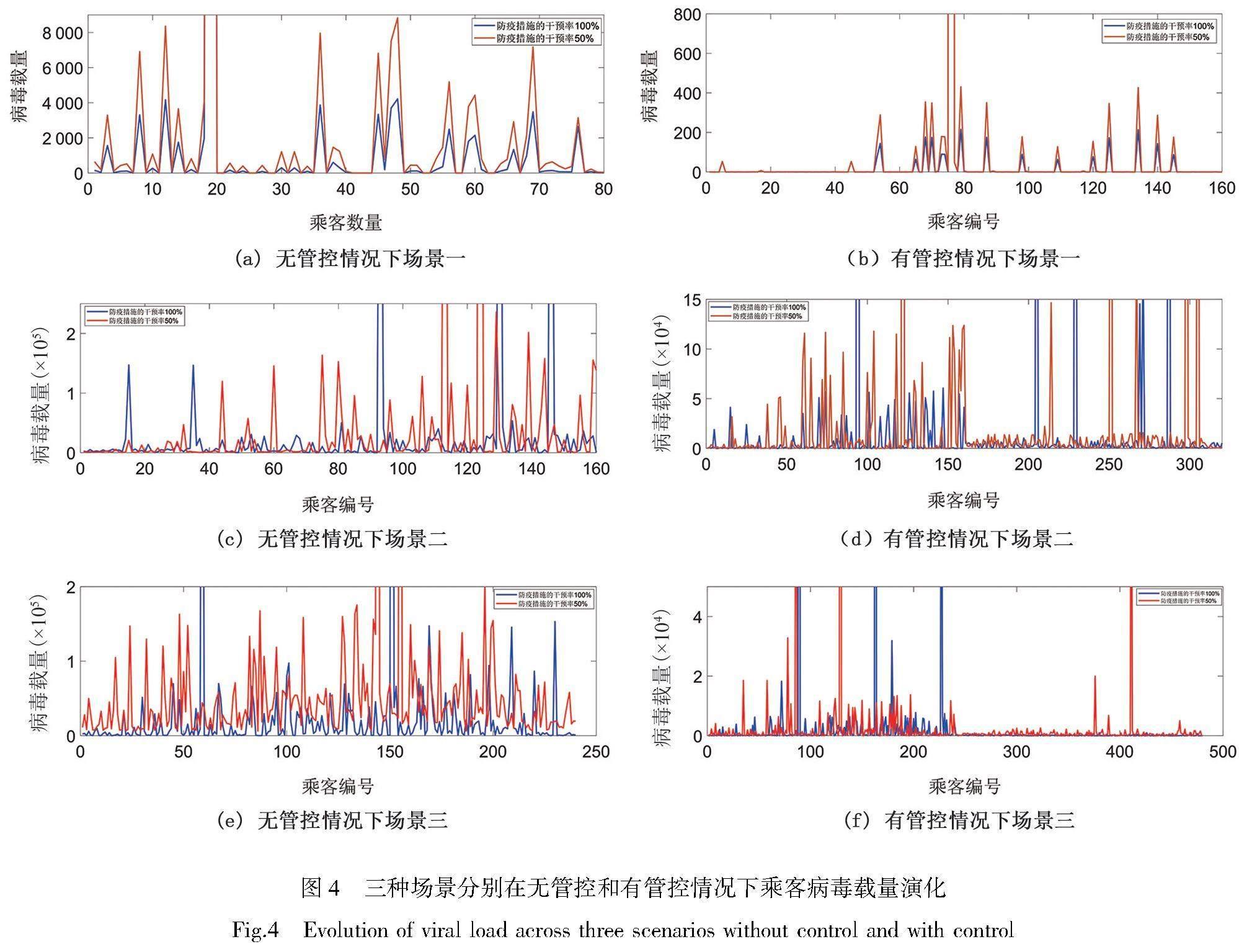
仿真的地铁车厢为南京地铁A型车厢，其几何尺寸（长×宽×高）是24.0 m×3.0 m×3.8 m，每節车厢定员240人。为了研究乘客密度对病毒传播的影响，分别设置定员的1/3、定员的2/3、定员人数3个场景，即80人、160人、240人。每个场景初始时刻被感染的乘客比例为10%，其中超级传播感染者占被感染乘客的比例为20%。由于车厢的尺寸是固定的，因此人数越多，密度越大，乘客之间的距离越小。仿真结果如图4。每组图包括无管控和有管控两种情况，无管控是指无论乘客体内的病毒数量多大，都允许其乘车。有管控是指基于病毒载量进行管控，当乘客体内的病毒数量大于1 000个时，不允许该乘客乘车。每个图中有两条曲线，防疫措施的干预率取100%对应于α＝０，防疫措施的干预率取50%对应于α＝0.5。

社交距離通过乘客密度来反映，乘客密度大则社交距离小，乘客密度小则社交距离大。对口罩、消毒等防疫措施的干预率分别是50%和100%两种情况进行仿真。为对比分析有无管控措施情况下的病毒传播，每个场景进行两轮仿真。对于无管控的情况，所有乘客在第一轮结束时的病毒载量数值基础上，继续进行第二轮模拟，仿真结果如图4（a）、4（c）、4（e）所示。对于有管控的情况，第一轮仿真30 min后，对病毒载量超过1 000个的乘客进行隔离，禁止其上车，生成新的乘客上车从而保持车厢内总人数不变。由于补充了新的乘客，因此图4（b）、4（d）、4（f）的横坐标表示的乘客编号大于车厢内的乘客数量。未被感染的乘客继承上一轮模拟结束时的病毒载量数值，进行第二轮模拟。

以上场景的仿真结果表明：对病毒载量大于阈值1 000的乘客进行管控，禁止其乘车，可将所有乘客的病毒载量降低一个数量级;随着乘车人数的增多，乘客密度增大，病毒传播增强，个体病毒载量增加较快。

为展示乘客个体病毒载量随时间的变化，对两种情况进行了仿真，情况1：车厢人数为80人、防疫措施控制有效率为100%；情况2：车厢人数为160人、防疫措施控制有效率为50%。仿真时长为1 h，如图5所示。与情况1相比，情况2的个体的病毒载量多一个数量级。

3 结论

本文利用物质守恒和随机建模方法建立了病毒载量演化模型。基于Anylogic二次开发接口，对建立的病毒载量演化模型进行编程，实现了地铁乘客病毒载量的仿真。仿真分析了乘客密度、防疫措施的有效率、有无管控措施三个因素对地铁乘客病毒载量的影响。仿真结果表明，随着乘车人数的增多，乘客密度增大，病毒传播增强，个体病毒载量增加较快。对病毒载量大于1 000的乘客进行管控，禁止其乘车，可将所有乘客的病毒载量降低一个数量级。这表明根据乘客体内病毒载量的数量对其能否乘车进行管控是有效降低病毒传播的重要手段，为精准管控提供了理论依据。此外，每个场景初始时刻被感染的乘客比例设定为10%，其中超级传播感染者占被感染乘客的比例为20%。仿真结束时，超级传播感染者的病毒载量比普通传播者的病毒载量多出一个数量级，因此识别超级传播者并对其乘车进行管控是管理的重点。

参考文献：

［1］李小莉， 曹策俊， 刘伟华， 等. 考虑传染概率的政府防疫管控策略演化仿真[J]. 中国安全科学学报， 2023， 33（3）： 42-50. DOI： 10.16265/j.cnki.issn1003-3033.2023.03.0835.

[2]方丹辉， 周敏， 洪荭， 等. 考虑疫苗效力差异的封闭场馆疫情传播分析[J]. 中国安全科学学报， 2022， 32（7）： 121-127. DOI： 10.16265/j.cnki.issn1003-3033.2022.07.2366.

[3]马剑， 李慧文， 宋丹丹， 等. 校园通勤行人流时空伴随分析与疫情防控策略[J]. 中国安全科学学报， 2022， 32（9）： 86-93. DOI： 10.16265/j.cnki.issn1003-3033.2022.09.2737.

[4]施红生. 国内重大传染病疫情铁路交通防控模式效率评估[J]. 铁路节能环保与安全卫生， 2013， 3（1）： 32-38. DOI： 10.16374/j.cnki.issn2095-1671.2013.01.006.

[5]贾兴利， 周吴啸， 韩兴家， 等. 交通管控措施对市域新冠疫情传播的阻断效果分析[J]. 中国公路学报， 2022， 35（1）： 252-262. DOI： 10.19721/j.cnki.1001-7372.2022.01.022.

[6]陈国强， 刘澜， 陈玉婷， 等. 基于Wells-Riley模型的公交车辆内部COVID-19传播及防控研究[J]. 公路交通科技， 2022， 39（6）： 144-152. DOI： 10.3969/j.issn.1002-0268.2022.06.019.

[7]SUN C J， ZHAI Z Q. The efficiency of social distance and ventilation effectiveness in preventing COVID-19 transmission[J]. Sustainable Cities and Society， 2020， 62： 102390. DOI： 10.1016/j.scs.2020.102390.

[8]YAN Y H， LI X D， SHANG Y D， et al. Evaluation of airborne disease infection risks in an airliner cabin using the Lagrangian-based Wells-Riley approach[J]. Building and Environment， 2017， 121： 79-92. DOI： 10.1016/j.buildenv.2017.05.013.

[9]谢国， 金永泽， 姬文江， 等. 高速列车疫情风险评估与主动防护策略[J]. 交通运输工程学报， 2020， 20（3）： 110-119. DOI： 10.19818/j.cnki.1671-1637.2020.03.010.

[10]MA J X， QI X， CHEN H X， et al. Coronavirus disease 2019 patients in earlier stages exhaled millions of severe acute respiratory syndrome coronavirus 2 per hour[J]. Clinical Infectious Diseases， 2021， 72（10）： e652-e654. DOI： 10.1093/cid/ciaa1283.

[11]ZHANG X， WU J F， SMITH L M， et al. Monitoring SARS-CoV-2 in air and on surfaces and estimating infection risk in buildings and buses on a university campus[J]. Journal of Exposure Science & Environmental Epidemiology， 2022， 32（5）： 751-758. DOI： 10.1038/s41370-022-00442-9.

[12]SANCHE S， CASSIDY T， CHU P H， et al. A simple model of COVID-19 explains disease severity and the effect of treatments[J]. Scientific Reports， 2022， 12： 14210. DOI： 10.1038/s41598-022-18244-2.

[13]POPA A， GENGER J W， NICHOLSON M D， et al. Genomic epidemiology of superspreading events in Austria reveals mutational dynamics and transmission properties of SARS-CoV-2[J]. Science Translational Medicine， 2020， 12（573）： eabe2555. DOI： 10.1126/scitranslmed.abe2555.