水下采油树油管挂C型锁环高效力学分析
2024-04-28王星王宝富鞠少栋王世强岳明阳
王星 王宝富 鞠少栋 王世强 岳明阳


摘要:为了有效解决水下采油树与油管悬挂器锁紧时, C型锁环与其驱动部件接触非线性和大变形非线性导致的计算收敛困难、速度慢的问题,提出了一种直接在C型环上加载径向位移替代传统驱动部件加载的方式进行有限元分析,并结合与驱动部件之间的力学关系推导获取C型环力学分析结果的方法。建立了C型锁环在径向位移加载下的理论数学模型,通过有限元分析验证了理论模型的正确性;结合实际应用模型,验证了该力学分析方法可有效提升有限元分析的收敛速度,具有较强的可行性与高效性,对类似部件力学性能分析具有重要的借鉴意义。
关键词:水下采油树;油管挂;锁环;力学分析;有限元分析
中图分类号:TE952 文献标识码:Adoi:10.3969/j.issn.1001-3482.2024.02.006
水下采油树是海洋油气田利用水下生产系统模式开发时,安装在海底井口上的一类不可或缺的关键装备,连接着井下几千米生产管柱与海底数十千米的油气输送管道,承载油气安全可控生产的重要功能,对其可靠性和稳定性要求极高,而采油树本体部分与油管悬挂器之间的C型环力学性能的优劣将直接影响到整个水下采油系统的稳定可靠性。C型环通常利用其弹性径向膨胀和径向收缩功能实现结构的锁紧和解锁,而C型环的张开和收缩需要驱动装置产生的径向力实现,驱动装置再和连接装置连在一起,从而通过对连接装置进行操作而实现C型环的锁紧与解锁。王军[1]等人对水下H4连接器的关键锁紧部件C型环进行了力学分析,但其主要是基于驱动应力推演出变形量和应力值,没有从设计位移量反演到驱动载荷,并且未考虑C型环拥有自由端下其变形后不再是圆形的基本前提,也未考虑剪力和周向力对变形的影响;除此以外,C型环的应力计算还来自于NACE TM0177和 GB/T1597015标准的应用和延伸,其目的均是通过C型环试验来确定硫化氢应力开裂的临界值,其中通过螺栓连接的方式施加载荷,避开C型环自由端的非线性问题,其理论模型不适用于有自由端开口的C型环[2-3];而对C型环的弹性径向膨胀和弹性收缩的有限元力学分析文章基本没有涉及,如AMBUJ SHARMA主要是考虑C型环用平面上测量的应变和三维有限元模拟的差异性[4];G.H. Kim等人则对C型环密封优化设计进行了分析,其径向变形较小,更多考虑径向上应力过高后产生塑性永久变形对密封性能的影响[5];张宝生主要论证了变截面开口圆环的强度计算方法,以便于变截面开口环产生均匀的弹力[6];史文谱针对开口薄壁环等速旋转的情形进行应力分析,其主要考虑离心力作用下,开口环的膨胀问题[7];刘洋利用能量原理对过盈连接的开口圆环力学模型进行研究,其基本假设为开口圆环张开后仍然为圆形,该假设仅适用于小曲率开口圆环[8];王强用动态光弹性法研究了冲击载荷作用下开口圆环的动应力分布,比较了动态和静态荷载作用下应力分布的差异[9];李文静利用三维有限元对弹簧结构C型环进行力学分析并与试验结果进行对比,验证了其密封性能,但缺少对理论分析的探索[10]。但晨归纳了用于断裂韧度测试的C形环小试样的规则化方法与应用[11],并进一步探索了C形环小试样疲劳裂纹扩展试验方法与应用[12];谢尘通过C型环试样淬火及深冷处理应力的演变进行数值研究[13];陆峰对复合材料LY12CZ铝合金的C-环应力腐蚀性能的影响进行了研究[14],它们的基本假设均为圆形,也仅适用于小曲率的开口圆环。
第53卷第2期王星,等:水下采油树油管挂C型锁环高效力学分析石油矿场机械2024年3月综上所述,目前国内外研究尚无考虑C型环自由端变形及接触非线性问题的有效力学分析方法,本文在前人研究基础上优化建立了C型环理论分析模型,同时应用直接在C型环上加载径向位移替代驱动部件加载进行有限元分析,并通过C型环与驱动部件之间的力学关系反推获取C型环力学结果的方法,有效解决了C型环与其驱动部件的接触非线性、几何非线性和大变形问题,最后结合实际应用模型验证了该力学分析方法可有效提升有限元分析的收敛速度,具有较强的可行性与高效性。
1径向位移加载下的C型环力学理论分析
1.1C型环在径向设计位移下的刚体位移分布 理论分析
C型环的受力是基于驱动环轴向向下移动,通过二者之间的接触斜面而产生摩檫力和斜面法向支撑力,这两种力在水平径向上分力的合力即为C型环的径向力,C型环径向力是径向位移的函数。C型环内侧施加相同的径向位移,假定忽略C型环的弹性变形量,通过图1可以建立C型环各点的水平位移(x向)和竖向位移(y向):
Dradial(x)=Dradial cos(θ)(1)
Dradial(y)=Dradialsin(θ)(2)
式中: Dradial(x)为设计的径向位移在x方向的分量,mm;Dradial(y)为设计的径向位移在y方向的分量,mm;Dradial为设计的径向位移,mm,径向位移的大小可通过C型环的设计变形量确定;θ为C型环横截面与x轴的夹角,(°),θ∈[α,π]。
由于C型环有2α的开口,所以C型环在开口端即为自由端(B-B截面),其总位移会远大于A-A截面处的位移,而总位移是刚体位移和变形位移的总和,刚体位移可以通过式(1)和式(2)求解,变形位移则需要通过求解C型环的刚度来获取。又由于C型环几何缺口导致的刚度变化很难获取解析解,通常采用有限元方法求解其形变位移量。也可近似采用能量法计算C型环的变形量。
图1以x轴对称的一半C型环变形前后示意图
1.2C型环在径向受载下的变形理论分析
忽略曲率的影响 ,采用能量法計算变形量与作用力之间的关系。在图2中任意截面M-M处的弯矩 M(φ)、轴向力 Fq(φ) 和剪切力 Fs(φ) 分别可表示如下 ,计算位移时,对于曲杆应令dx = ds,由图3知ds= Rdθ,故有:
M(φ)=∫παRsin(φ-θ)σradial Rdθ(3)
Fq(φ)=∫πασradial sin(φ)wRdφ(4)
Fs(φ)=∫πασradial cos(φ)wRdφ(5)
根据摩尔积分法,在B-B端分别施加x向和y向的单位载荷,其端部的变形量如下:
Δ=∫f1(M(φ))+∫f2(Fq(φ))+∫f3( Fs(φ))(6)
Δx=∫π2ασradial R2(1-cosφ)Rsinφ)EIzRdφ+
∫ππ2σradial R2(1-cosφ)R(1+sinφ)EIzRdφ+
∫πασradialcos(φ)2wEARdφ=
σradialR4EIz(2π+9-cos(2α)+4cosα4)+
σradialRwEA(2π-2α-sin(2α)4(7)
Δy=∫πασradial R2(1-cosφ)2REIzRdφ+
∫πασradial sin(φ)2wGARdφ=
σradialR4EIz(6π-2α+8sinα-sin2α4)+
σradialRwGA(2π-2α+sin(2α)4)(8)
Δ=Δx2+Δy2(9)
式中:Δ为总变形量,mm;E为杨氏模量,MPa,G为剪切模量,MPa;f1为弯矩作用下对C型环产生的变形的函数,mm;f2为轴向力作用下对C型环产生的变形的函数,mm,f3为剪力作用下对C型环产生的变形的函数,mm;Iz为惯性模量,mm4;R为C型环名义半径,mm;α为C型环开口角度的半角,(°);A为C型环的横截面积,mm2。
叠加式(1)和式(2)得到的刚体位移和本部分式(9)得到的总变形量,其总和即为B-B端的总体位移,即Δtotal=Δ+Dradial。
图2以x轴对称的一半C型环受力分析图
1.3C型环在径向设计位移下的应力分布理论 分析
基于参考文献对C型环的理论分析,本文假定在径向位移均布加载下,其截面径向应力σradial在周向上分布是均匀的,在产生的弯矩、剪力和轴力作用下,其A-A端应力最大。如图3所示。
图3C型环响应载荷受力分析图
根据弯矩方向,C型环的内侧沿周向方向(逆时针)产生张应力,C型环的外侧沿周向方向(顺时针)产生压应力,结合周向截面载荷,其A-A端的周向应力表达式为:
σhoop=σ1±σ2=FhoopA±Mz yρS(10)
式中: σhoop为周向应力,MPa;σ1为周向截面载荷Fhoop产生的周向应力,MPa;σ2为弯矩产生的周向应力,MPa,其中正代表拉应力并与σ1方向一致,负代表压应力,并与σ1方向相反;Fhoop为周向载荷,N,Fhoop=Fs(π);对复杂截面可以简化成规则的几何形状,本文简化为矩形;Mz为应力计算点受到的弯矩,N·mm;Mz=M(π);y为应力计算点到中性轴的距离,mm;ρ为应力计算点的曲率半径,ρ=r+y,r为中性层的曲率半径[15],r=tln(d/(d-2t)),mm;S为整个截面对中性轴的静矩,mm3,S=A·(R-r)。
对于C型环,应力的最大值出现在A-A截面(图3所示),该截面处的参数为:
A=w·t(11)
yo=d/2-r(12)
yi=r-(d/2-t)(13)
ro=d/2(14)
ri=d/2-t(15)
R=(d-t)/2(16)
式中:yo,yi分別为C 型环外壁和内壁距中性层曲率半径 r处的距离,mm;ro,ri分别为C 型环外壁和内壁曲率半径,mm。
把式(3)和式(11~16)全部带入式(10),得到A-A截面内外表面处的应力(注意:M中的θ角为假定的集中加载中心,即径向分布位移施加后的载荷集中点,不是A-A处的角度)为:
σhoop(o)=FhoopA-MyρS=
-6Rsinα)t-(d-2r)(1+cos(α)+R2 σradial)wtd(R-r)(17)
σhoop(o)=FhoopA+MyρS=
-6Rsinαt+(2r-d+2t)(1+cos(α)+R2 σradial)wt(d-2t)(R-r)(18)
式中:σhoop(O),σhoop(i)分别为C型环外侧和内侧的周向应力,MPa。
2径向位移加载法理论模型有限元验证
2.1载荷与边界条件
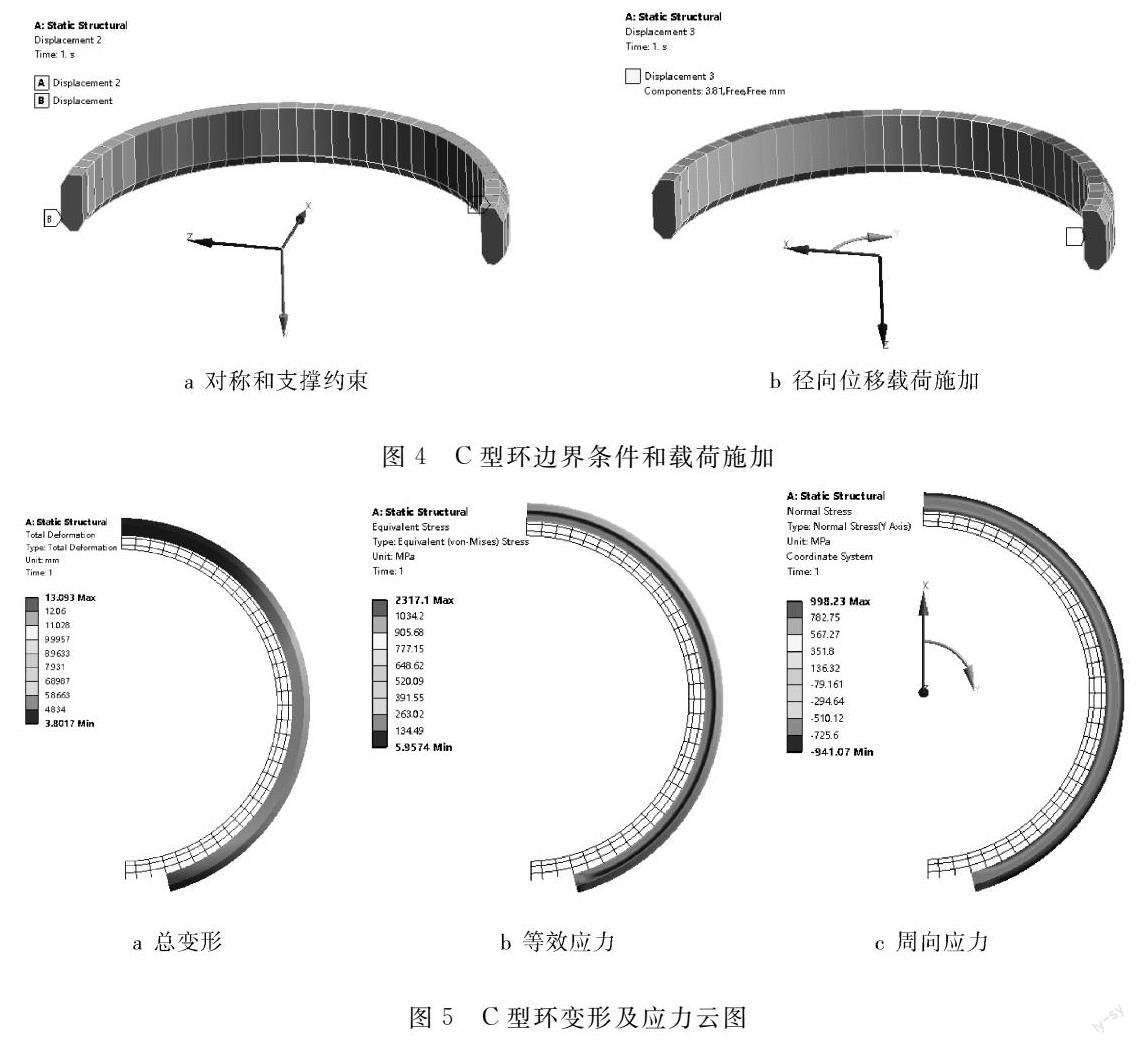
由于本文的分析也未考虑C型环变形后不再是圆形的基本假设,针对C型环部分进行有限元计算。计算的输入包括:C型环有限元分析模型,材料参数杨氏模量为2×105 MPa,泊松比为0.3,底部为y方向自由度为0,径向上施加设计的位移3.81 mm(0.15英寸),显示如图4所示,其中在笛卡尔坐标下,A为对称约束Ux=0(笛卡尔坐标下,如图4a所示),B为底面支撑约束Uy=0。C为施加径向载荷Ux=3.81 mm(柱坐标下,如图4b所示)。前处理完成后通过Workbench20.0R2进行结构静力求解。
图4C型环边界条件和载荷施加
2.2应力和变形情况分析
如图5所示,其位移总量为刚体位移(径向加载位移)加弹性变形量,自由端的总位移量13.09 mm明显大于A-A端的总位移量3.81 mm,A-A端的总位移量和径向施加位移接近,故A-A端无变形量,和理论分析一致。C型环的Vonmisess应力图以及周向应力图可以看到明显的中性层,在Vonmiss应力图中,外侧和内侧的等效应力更高,这是弯矩产生的拉应力和压应力的原因;在周向应力图中可以看到内侧为正应力(受拉),外侧为负应力(受压)。其A-A截面上的平均应力及弯曲应力沿C型环厚度方向的分布如图6所示。
图5C型环变形及应力云图
图6C型环A-A端其周向应力线性化图
3径向位移加载法实例应用
以水下井口套管挂锁紧为例,其结构示意如图7所示,共包含C型环和驱动环两个部件。C型环在驱动环轴向向下驱动过程中,由于接触斜面会产生两个载荷,一个为轴向向下载荷,它传递到C型环,避免其跳动,另一个载荷为径向膨胀载荷,它使锁环不断张开到设计位置。驱动环轴向向下到设计位置后通过倒齿结构防止其轴向回弹,由此确保锁环在径向上的支撑不变。此时,在驱动环到位后,锁环与外侧的结构配合实现锁紧;当需要解锁时,上提驱动环,锁环释放其弹性能而收缩,退出与之配合的锁紧结构实现解锁。能否成功实现锁紧和解锁的关键在于C型环不能进入塑性状态确保其可以弹性张开和收缩;另外一个关键是驱动力应在合适的范围,不能超过平台的额定驱动载荷,一般轴向驱动载荷最好在266 893 N范围以内。
图7套管挂锁紧结构示意图
3.1有限元计算
不能产生塑性变形和合适的轴向驱动力两个关键点都需要进行有限元的力学核算,本文考虑仅把C型环放入其中,计算其非线性的部分,而对驱动环进行理论计算,获取其轴向驱动力。该方法考虑了C型环的非线性并避开了C型环和驱动环之间的非线性接触,从而极大地提高了计算效率。其主要输入参数如图4所示,载荷分布如图5所示,撑开锁环到设计位置的径向力如图8所示,当径向位移为3.81 mm时,其径向力为2 759 N。
图8锁环不同撑开位置下的径向力
3.2驱动环力学分析
由于驱动环为整环,无缺口的非线性问题,考虑其一个截面作为受力分析对象,如图9所示,x代表径向方向,y代表轴向方向,周向垂直于x,y截面。驱动环在轴向加载力F下,被接触斜面分解成沿斜面向上的摩檫力f和垂直与斜面的支持力N。
图9驱动环力学分析
由于径向上需提供锁环的张开力,根据静力平衡原理,其力学表达如下:
F=fsinβ+Ncosβ(19)
Fradial=Nsinβ-fcosβ(20)
f=μN(21)
式中:F为驱动环轴向驱动力,N;β为接触斜面与水平方向的夹角,(°),本文取60°;Fradial为作用在C型环上的径向力,N;μ为接触斜面摩擦因子,本文取0.1。
式(19)~(21)中,一共3个方程并有3个未知参数N,f,F;可联立求解出,其中驱动环轴向力的数学表达式如下:
F=Fradial (μsinβ+cosβ)sinβ-μcosβ(22)
再结合图8中的公式,Fradial=724.11Dradial,并代入式(22),获得C型环设计径向位移与驱动环所需轴向力之间的关系为:
F=724.11Dradial (μsinβ+cosβ)sinβ-μcosβ(23)
以Dradial作为自变量,F作为因变量进行计算,获得的曲线如图10。
图10不同C型环设计位移对应的驱动环轴向力
综上所述,设计的C型环径向位移所对应的驱动力较小,且截面应力在弹性范围内,弯矩应力在C型环内外侧较高,可考虑在内外侧交错增加适量的槽,降低其抗弯刚度,从而确保C型环在弹性范围内。在工厂测试和实际应用中,设计的C型环均能以较小的载荷打开2 669 N左右,且未发现明显的塑性变形,进一步验证了其设计的有效性。
4 结论
1)通过拆分计算,建立了C型环可应用工程设计的理论数学模型;结合C型环在水下实际的锁紧和解锁功能,考虑到自由端带来的非线性问题,确定C型环部分用有限元计算的必要性和合理性。
2)形成了一套直接在C型环上加载径向位移,通过C型环与驱动部件之间的力学关系反推获取C型环力学结果的高效力学分析方法,能够有效解决水下采油树与油管悬挂器锁紧时,C型锁环与其驱动部件接触非线性和大变形非线性导致的计算收敛困难、速度慢的问题。
3)通过详细描述C型环有限元计算的整个流程,尤其结合驱动环的实际情况,高效准确地建立起驱动力与设计位移之间的理论表达式,为水下采油树系统关键部件力学分析提供了重要的方法参考。
参考文献:
[1]王军,罗晓兰,段梦兰,等.深水采油树井口连接器锁紧机构设计研究[J].石油矿场机械,2013,42(3):16-21.
[2]赵华莱,姜放,李珣,等.C型环试验的加载应力计算[J].天然气与石油,2007(2):21-24.
[3]练章华,梁建坤,王裕海,等.C型环环向应力与加载载荷的公式推导与验证[J].西南石油大学学报(自然科学版),2019,41(5):161-168.
[4]AMBUJ SHARMA,CHARLES E. BAKIS,Analysis of Elastic Stresses in Thick,Polar–Orthotropic,C-shaped Rings[J].Composite Materials, 2004,38(18):25-32.
[5]G.H. Kim, N.I. Her, H.T. Kim.A design study on metal C-ring seals[M].Korea Institute of Fusion Energy,Daejeon, 2022:305-333.
[6]張保生.匀弹力变截面开口圆环的弹力集度及强度计算[J].机械科学与技术,1994(3):95-97.
[7]史文谱,刘爱荣,王媛.等速旋转开口薄壁圆环的力学分析问题[J].机械强度,2010,32(1):134-138.
[8]刘洋,杨晋,张剑平,等.开口圆环过盈联接力学分析[J].航空精密制造技术,2014,50(4):55-57.
[9]王强,张振辉,王祥林.冲击荷载作用下开口圆环的动应力分析[J].黑龙江大学自然科学学报,1998,15(2):66-69.
[10]李文静,沈明学,彭旭东,等.弹簧结构参数对赋能型金属C形环力学行为及密封性能的影响[J].润滑与密封,2016,41(11):71-77.
[11]但晨,蔡力勋,包陈,等.用于断裂韧度测试的C形环小试样的规则化方法与应用[J].机械工程学报,2015,51(14):54-65.
[12]但晨,蔡力勋,包陈.C形环小试样疲劳裂纹扩展试验方法与应用[J].工程力学,2015,32(12):27-32.
[13]谢尘,黎军顽,封源,等.C型环试样淬火及深冷处理应力演变的数值研究[J].材料热处理学报,2015,36(S2):248-255.
[14]陆峰,张晓云,汤智慧,等.复合材料对LY12CZ铝合金C-环应力腐蚀性能的影响[J].材料工程,2003(7):3-6.
[15]刘鸿文. 材料力学[M].北京:人民出版社,1980.2024年第53卷
