区间量测下自适应交互多模型箱粒子滤波机动目标跟踪

张俊根

(北方民族大学 电气信息工程学院,银川 750021)

0 引 言

目标跟踪是利用如雷达、红外等传感器获得目标的量测信息对目标状态进行估计,在军事和民用领域应用非常广泛[1-2]。

由于目标动态建模与量测建模坐标系转换过程中以及量测传感器自身物理特性造成模型的非线性问题,贝叶斯最优估计通常不能获得解析解。为此,相关学者在卡尔曼滤波基础上,提出了改进方法,如改进极性扩展卡尔曼滤波[3]、增广系综卡尔曼滤波[4]、无迹卡尔曼滤波[5]及伪线性卡尔曼滤波[6]等。当系统非线性、非高斯特性较强时,这类算法滤波性能急剧下降甚至会发散。粒子滤波(Particle Filter,PF)是一种基于蒙特卡罗积分的非线性、非高斯滤波器,具有更好的灵活性、更优的估计精度及更广的适用性,逐渐成为了研究目标跟踪问题的热点和有效方法[7]。粒子滤波的一个主要缺点是计算复杂度高[8],在实时目标跟踪的应用中有局限性。

对于机动目标跟踪,由于目标运动状态不单一且无法预测,结合交互多模型(Interacting Multiple Model,IMM)算法是常用的解决方法[9-10]。IMM算法利用多个模型来适应机动目标的运动,通过马尔可夫转移概率矩阵实现模型间的转换。但是,传统的IMM算法是根据先验信息将转移概率矩阵设定为固定的主对角占优矩阵,不能依据后验信息对转移概率进行实时调整,将导致模型切换滞后。当先验信息不足或者不准确,使用固定的转移概率矩阵往往会导致目标状态估计不准确,滤波性能下降,甚至算法失效[11]。为此,许多学者提出了改进方法[12-15]。

在实际应用中,比如,在复杂分布系统和无线传感网络中,量测会受到未知分布的边界误差影响,使得该类非标准的量测呈现区间形式[16]。为解决区间量测条件下的机动目标跟踪问题,文献[17]提出了交互多模型箱粒子滤波(Interacting Multiple Model Box Particle Filter,IMMBPF)算法,改善了目标跟踪效率,但在目标跟踪过程中存在模型切换和跟踪精度方面的不足。因此,本文充分利用后验信息,对马尔可夫转移概率矩阵进行修正,提出一种自适应交互多模型箱粒子滤波(Adaptive Interacting Multiple Model Box Particle Filter,AIMMBPF)算法。仿真结果表明,该算法的模型匹配度更优,且目标跟踪精度比原有IMMBPF算法高。

1 问题描述

区间量测下多模型目标跟踪系统可以由一组状态方程和量测方程表示：

xk+1=Fmkxk+wk,mk

(1)

[zk]=H(xk)+vk

(2)

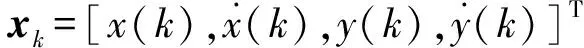
IMM算法中,利用M个模型对目标运动进行模拟,从k时刻的模型α变换到k+1时刻的模型β,可以建模为一个概率已知且时不变的马尔可夫链,即

(3)

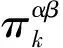
2 基于自适应IMMBPF的目标跟踪算法

2.1 转移概率矩阵自适应更新策略

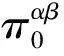
(4)

(5)

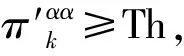
(6)

经过验证可以看出,式(6)修正的转移概率矩阵仍然满足两个基本要求：

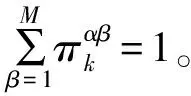
2.2 AIMMBPF算法

本文提出的AIMMBPF算法是在IMMBPF算法[17]基础上增加了转移概率矩阵自适应更新步骤,并做了相应计算式子上的改变,主要包含以下6个迭代步骤：箱粒子生成;模型交互;箱粒子滤波;模型后验概率更新;转移概率矩阵更新;状态融合输出。

1)箱粒子生成

利用k-1时刻的区间量测[zk-1],生成新生箱粒子。对于每一个[zk-1],新生箱粒子密度用一组均匀分布的概率密度函数的和来近似,如下式所示：

(7)

新生箱粒子由两部分组成：位置分量[p]和速度分量[u],即[xb,k-1]=[[p]T,[u]T]T,[p]=[H-1]([zk-1]),H-1代表量测函数的反函数,[u]≈[support(p0(u))]为包含先验值p0(u)的均匀分布,每个箱粒子的权值为1/Nb。

(8)

式中：Np为存活箱粒子的最大数;N为箱粒子总数,N=Nb+Np。

2)模型交互

k-1时刻,计算α模型转移到β模型的概率：

(9)

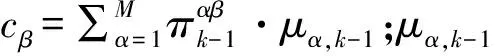
通过下式计算,得到模型β的交互箱粒子：

(10)

式中：i=1,2,…,N。

3)箱粒子滤波

对于模型α,计算预测箱粒子为

(11)

预测区间量测为

(12)

计算箱粒子的权值,并进行归一化：

(13)

(14)

计算α模型的箱粒子滤波输出：

(15)

4)模型后验概率更新

对于任一模型α,计算模型的似然函数为

(16)

更新模型后验概率为

(17)

5)转移概率矩阵更新

利用式(6),对转移概率矩阵进行实时更新。

6)状态融合输出

利用更新的模型后验概率,对各模型滤波输出的区间中间值进行加权融合,得到更新的目标状态：

(18)

式中：mid[xα,k|k]为区间[xα,k|k]的中间值。

3 仿真实验与分析

为了验证所提出的AIMMBPF算法的性能,并与交互多模型粒子滤波(Interacting Multiple Model Particle Filter,IMMPF)算法和IMMBPF算法作对比。进行100次蒙特卡罗仿真实验,利用均方根误差(Root Mean Square Error,RMSE)评价算法的性能,定义如下：

(19)

(20)

式中：Nt表示目标跟踪总时间。

3.1 仿真实验设置

系统模型由式(1)和式(2)描述,假设目标在二维平面上运动,目标初始位置为(100 m,0 m),初始速度为(100 m/s,80 m/s)。目标在0～20 s做匀速直线运动,在21～40 s做匀速右转弯运动,在41～60 s做匀速直线运动,在61～80 s做匀速左转弯运动,在81～100 s做匀速直线运动。

目标运动模型集选用以下3个模型：匀速直线CV模型、匀速右转弯CT模型和匀速左转弯CT模型。令mk∈{1,2,3},分别表示以上3个模型,状态转移矩阵Fmk分别为

(21)

(22)

式中：T为采样间隔,T=1 s;ζ为转弯角速度,ζ=5 °/s表示左转弯,ζ=-5 °/s表示右转弯。

3个模型的过程噪声协方差矩阵Qmk设为

(23)

初始模型概率为μ1,0=μ2,0=μ3,0=1/3,模型转移概率矩阵初始值设为

(24)

量测函数H(xk)为

(25)

量测噪声协方差矩阵如下：

(26)

区间量测长度设为150 m,新生箱粒子的速度分量服从均匀分布U[-150 m/s,150 m/s]。

IMMPF的总粒子数为1 500,新生粒子数为500。对于IMMBPF和AIMMBPF算法,总箱粒子数为60,新生箱粒子数为10。转移概率自适应更新阈值设为0.9。本文所有实验都是在同一台电脑环境(CPU型号为i7-7500U,内存为4 GB)下通过Matlab实现的。

3.2 算法性能对比

图1给出了某次实验中3种算法的目标跟踪轨迹对比,可以看出,本文提出的AIMMBPF算法、IMMPF算法和IMMBPF算法都能实现对机动目标的有效跟踪。

图1 3种算法的目标跟踪轨迹对比Fig.1 Target tracking trajectories of three algorithms

经过100次蒙特卡罗实验后,得到了3种算法的位置均方根误差和速度均方根误差,分别如图2和图3所示。对图2和图3的数据进行分析,根据式(20),分别得到位置和速度估计的均方根误差的均值,如表1所示。

表1 3种算法的状态估计ARMSE对比Table 1 State estimation ARMSE of three algorithms

图2 3种算法的位置均方根误差Fig.2 Position RMSE of three algorithms

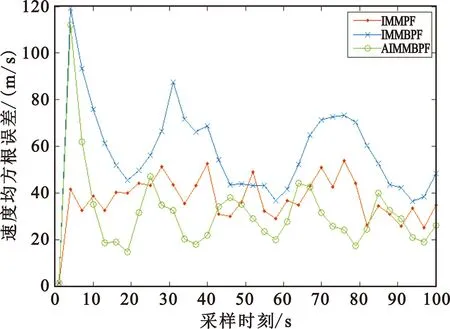
图3 3种算法的速度均方根误差Fig.3 Velocity RMSE of three algorithms

从图2、图3和表1可以看出,在位置跟踪方面,IMMPF算法的误差最大,IMMBPF算法次之,AIMMBPF算法的误差最小。从ARMSE指标看,AIMMBPF算法相比于IMMPF算法和IMMBPF算法的跟踪精度分别提升了12.74%和10.53%。在速度跟踪方面,IMMBPF算法的误差最大,主要是由于IMMBPF算法在压缩箱粒子时没有考虑目标速度分量,在模型匹配度不高的情况下速度跟踪劣势更加明显。AIMMBPF算法由于模型转移概率能自适应实时修正,模型匹配度更高,跟踪误差最小。相比于IMMPF算法和IMMBPF算法,AIMMBPF算法的ARMSE分别减小了15.49%和44.57%。

图4～6分别给出了3种算法的各模型概率,可以看出,本文提出的AIMMBPF算法能使系统迅速调整到匹配模型,且匹配模型的概率更加接近于1,不匹配模型的概率更加接近于0,而IMMPF算法和IMMBPF算法模型的切换及主次模型都不够分明。

图4 IMMPF算法的各模型概率Fig.4 Model probability of IMMPF algorithm

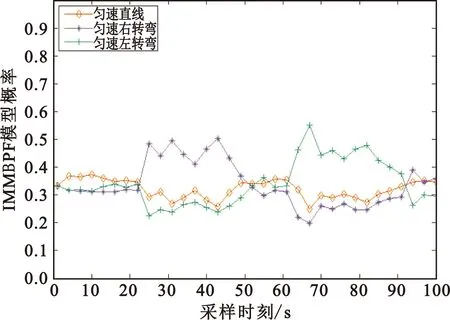
图5 IMMBPF算法的各模型概率Fig.5 Model probability of IMMBPF algorithm

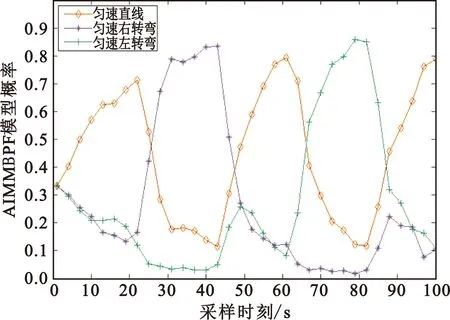
图6 AIMMBPF算法的各模型概率Fig.6 Model probability of AIMMBPF algorithm

本文利用运行时间来评价算法计算复杂度。不同算法执行一次完整的目标跟踪的运行时间如表2所示,可以看出,IMMPF算法耗时最大,AIMMBPF算法的运行时间约为IMMPF算法的20%,由于增加了模型转移概率自适应修正计算步骤,比IMMBPF算法耗时略大。

表2 3种算法的运行时间对比Tab.2 The running time of three algorithms

3.3 模型转移概率初始值对算法性能的影响

本节通过改变模型转移概率初始值来评价算法的性能。模型转移概率初始值是根据文献[12]的方法进行设计,即

(27)

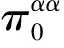
图7 不同模型转移概率初始值下3种算法的位置ARMSEFig.7 Position ARMSE of three algorithms under different model transition probability initial values

图8 不同模型转移概率初始值下3种算法的速度ARMSEFig.8 Velocity ARMSE of three algorithms under different model transition probability initial values

3.4 滤波初始误差对算法性能的影响

本节通过改变滤波初始误差来评价算法的性能。对目标初始状态x1施加一个标准正态分布噪声：

x1+ε·diag(80,40,80,40)·randn(4,1)

(28)

式中：diag(·)表示对角矩阵;randn(·)表示标准正态分布;ε是误差系数。仿真设定ε在0～2内均匀变化,步进为0.2;其他参数不变。图9和图10分别给出了这3种算法的位置和速度ARMSE对比。

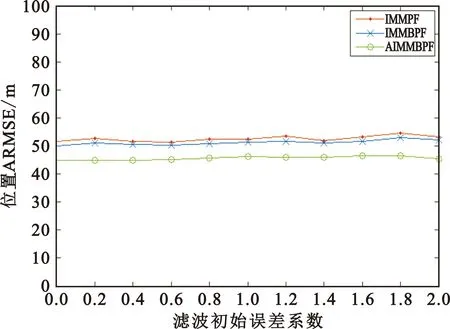
图9 不同滤波初始误差下3种算法的位置ARMSEFig.9 Position ARMSE of three algorithms under different initial filtering errors

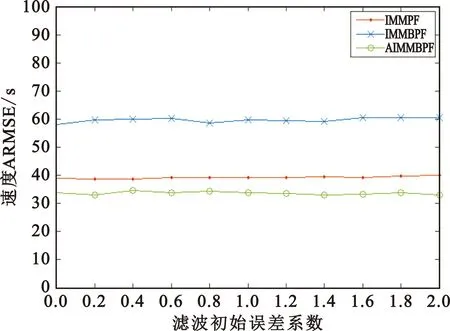
图10 不同滤波初始误差下3种算法的速度ARMSEFig.10 Velocity ARMSE of three algorithms under different initial filtering errors

从图9和图10可以看出,这3种算法在不同滤波初始误差下,目标位置和速度估计误差变化都较小,跟踪精度都比较稳定,表明这些算法对滤波初始误差不敏感,基本不会受到滤波初始误差的影响。

4 结束语

本文针对区间量测下的机动目标跟踪问题,在IMMBPF算法的基础上提出了一种自适应IMMBPF算法。该算法能够充分利用后验信息,对模型转移概率矩阵进行自适应更新,可以增大匹配模型的概率,同时减小非匹配模型的影响。仿真结果表明,本文提出的AIMMBPF算法相比于现有算法拥有更优的模型匹配度和目标跟踪精度。

下一步工作将重点研究模型集设计方法,将强跟踪修正输入估计模型与自适应交互多模型相结合,进一步提高目标跟踪精度。