分布式机器学习在RIS辅助的无线信道估计中的应用

陈 静,邓炳光,冀涵颖

(重庆邮电大学a.通信与信息工程学院;b.光电工程学院,重庆 400065)

0 引 言

近年来,可重构智能超表面(Reconfigurable Intelligent Surface,RIS)技术逐渐引起了业界的广泛关注和研究,被认为是6G关键技术之一[1-2]。RIS是一种由大量无源器件组合而成的电磁活性表面[3]。具体而言,RIS通过在平面上集成大量低成本的无源反射元器件来辅助无线通信[4],可以分别独立修改通信信道的幅值或者相位[5]。这种相移或者幅度的变化由连接基站(Base Station,BS)的回程控制链路来进行相应的操作,可以对接收到的由BS发射的信号进行相应的调节,有助于改进信道的覆盖率,灵活应对不同无线通信信道传输环境。

在RIS辅助下行信道估计的通信系统中,所有的RIS单元都是无源的,因此很难对级联信道进行分别估计,所以普遍情形下,用户都是先对基站发射到RIS信号的信道进行估计,再从RIS反射的信号到用户的信道进行估计。针对无线通信系统中RIS辅助信道估计的方案如最小二乘估计(Least Squares Estimation,LS)[6]以及归一化均方误差(Normalized Mean Squared Error,NMSE)估计[7],其性能很大程度上依靠天线的阵列输出的完善程度,从而得到可靠的信道估计精度。而导频开销与天线阵列规模以及部署的RIS的规模有关,由于在实际运用中需要较复杂的天线阵列和较大的RIS尺寸,所以导致下行信道估计导频开销巨大。为了解决数组数据中存在的缺陷或损坏问题,同时减轻导频开销的巨大负担,本文引入了机器学习技术[8]。

在机器学习辅助下行链路信道估计的应用中[9-11],都仅仅考虑集中学习方案,需要将所有的输入输出数据对上传到BS,在BS训练完成后将模型参数返回给用户。然而这种方式需要巨大的通信开销,同时用户数据的隐私性也不能得到很好的保证。

针对如何有效降低通信开销以及保障用户数据的隐私性等问题,文献[12]利用联邦学习框架设计了一个卷积神经网络(Convolutional Neural Network,CNN),使训练过程在本地数据集上运行,不需要将数据发送给基站,从而大大降低了通信开销;文献[13]则是采用分布式机器学习框架单独训练本地深度神经网络(Deep Neural Network,DNN)模型,通过在中央服务器上聚合本地的DNN模型,将数据梯度向量传递给中央服务器,有效保障了用户数据的隐私性;文献[14]进一步考虑了每个用户处于不同通道场景的情况,利用分布式机器学习对每个通道场景区域进行了卷积神经网络的构建,有效提高了信道估计的准确率。相对于集中式学习,采用分布式机器学习更能有效节约资源,更加具有实施性。

然而上述文献都未充分考虑到用户的移动性所导致的位置的随机性,这为下行链路的信道估计带来了巨大的挑战。为此,本文提出了一种基于区域交集的分布式机器学习方案(Switching Hierarchical Downlink Channel Estimation,SHDCH)。该方案利用分布式机器学习模型框架建立基站与用户的通信模型,同时考虑到不同信道的特征存在差异性,采用分层次神经网络对其进行相应的特征提取以及映射,最后利用区域融合方式,将映射后的信道模型进行相应的融合处理,融合后的模型能够针对移动用户所处的不同位置进行准确的信道估计。并且由于引入了分布式机器学习,也使得信道估计中通信开销有所降低。

1 系统模型

考虑由一个配置多根天线的基站和多区域多个配置单根天线的用户组成的通信系统,如图1所示,BS有M根天线分别与R个区域的K个用户进行通信,其中RIS由N个被动反射单元组成。分别考虑BS的M根天线以及RIS的N个元素对应的响应向量都为方形天线阵列分布。

假设RIS辅助的无线通信系统为频分工作模式[9]。用G∈N×M表示BS与RIS之间的信道,用fr,k∈1×N表示第r个区域中的第k个用户与RIS之间的信道。为便于信道分析,假设BS与用户之间的直接信道被障碍物阻隔,仅考虑由RIS反射的信道,则第r区域的第k个用户接收到的信号可以表示为

yr,k=fr,kΦGwr,kxr,k+zr,k

(1)

式中：xr,k表示发送给第r个区域第k个用户的功率归一化信号,且‖xr,k‖2=1;wr,k∈M×1表示波束赋形向量;Φ=diag{φ1,φ2,…,φN}表示在RIS处的相移矩阵,φN表示第N个RIS元素的相移系数;zr,k表示第r个区域第k个用户接收时的附加噪声,其分布服从循环对称复高斯噪声,均值为0,方差为1。

信道G和信道fr,k的构建采用多径瑞利衰落信道模型。给定G的表达式如下：

(2)

(3)

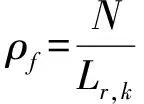
a(ϑ,φ)=ax(u)⊗ay(v)

(4)

式中：⊗表示克罗内克积;u≜2πdsinγlcos ϑ/λ,v≜2πdsin(γl)cos(ϑl)/λ,d表示天线间距,λ表示信号的波长,满足d=λ/2,且

(5)

通过表示Φ=[φ1,φ2,…,φN]将公式(1)进一步表示为

yr,k=Φdiag(fr,k)Gwr,kxr,k+nr,k=
ΦHr,kwr,kxr,k+nr,k

(6)

式中：Hr,k=diag(fr,k)G表示BS与对应用户之间的下行链路级联信道。

假设在一个时隙内信道模型不发生变化,由公式(6)可得,在第q个时隙的第r个区域的第k个用户的信道模型可以表示为

(7)

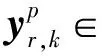
(8)

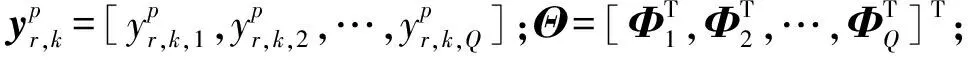
2 RIS辅助无线通信系统的信道估计

2.1 基于分布式机器学习训练

在设计的分布式机器学习模型中,需将CNN部署在用户侧,便于数据采集和处理。一旦全局CNN网络收集了不同区域的所有用户的数据集,将以下问题的作为优化目标来进行训练：

(9)

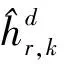
(10)

为了有效求解式(9),采用梯度下降法迭代进行求解,梯度向量更新公式如式(11)所示：

(11)

在分布式机器学习中,每一个用户都需要将自己的梯度向量发送给BS,从而对模型参数θ进行更新：

(12)

式中：θt表示第t次模型参数的值;K表示所有区域的用户。

用户只需要将梯度向量传送给BS,不需要本地数据上传给基站,所以不需要浪费用户大量的传输功率[15-17],可以提供更高的能源效率。

2.2 模型构建

本小节对提出的基于区域交集的DML模型进行模型构建。首先针对区域分类器,在数据收集部分引入了信道标签,故使用区域分类器的输出与区域索引标签的交叉熵作为损失函数。将训练后的模型用于用户所处的区域预测,根据预测概率,考虑用户是否处于区域交集处：如果用户不处于区域交集处,则直接提取该区域的特征;反之,如果处于区域交集处,即采用特征提取器对所涉及到的两部分区域分别进行特征提取,根据各区域的权重对信道进行不同程度的提特征提取。区域交集处的判决条件如(13)所示：

(13)

式中：Pr表示用户属于r区域的预测概率;Pr±1表示用户属于r区域的邻近区域;Pmax表示设定的最大概率值;Pmin表示设定的最小概率值。如果满足式(13),则判定用户处于区域r与其邻近区域的交集处,则需要按照式(14)对小区概率权重进行重新分配：

(14)

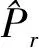
(15)

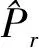
上述模型流程如图2所示。

图2 分层下行信道估计模型流程Fig.2 Flowchart of the hierarchical downlink channel estimation model

在提出的模型中,区域分类器是一个独立模块,而区域特征提取器和特征映射器是一个耦合的模块。针对本文提出的区域分类器,构建了一个5层的CNN模型。具体而言,该CNN模型的第一层为卷积层,由24个5×5的核滤波器和ReLU激活函数联合构建,用于对特征进行非线性变换;第二层为池化层采用的内核为2×2;第三层和第一层设置相同;第四层为池化层,采用的内核为2×2;第五层为线性层。而在特征提取器构建的CNN模型则是由4层卷积层组成,每一层都由24个5×5核滤波器组成。特征映射器是一个线性层,用于将特征提取器提取的特征进行相应的映射。值得注意的是,每一个区域都需要一个特征提取器以及相应的特征映射器。模型的完整网络架构如图3所示。

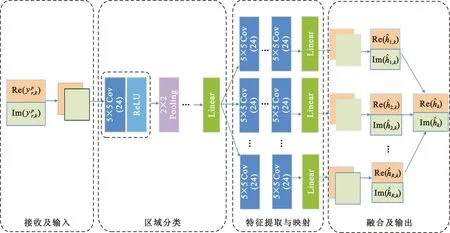
图3 SHDCH网络架构Fig.3 SHDCH network architecture

3 仿真与分析

3.1 仿真参数

为了显示本文提出分布式机器学习的区域切换方案的优越性,将信道估计的NMSE结果可视化展示[18]。

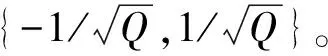
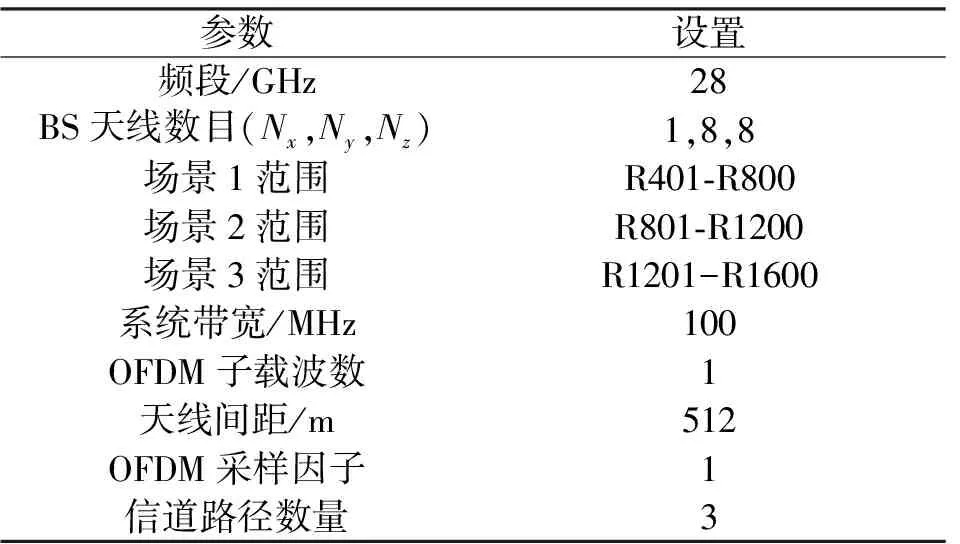
表1 DeepMIMO数据参数设置Tab.1 DeepMIMO data parameter setting

在用户数据集中,假设单个用户收集样本大小为20 000组,其中用90%作为CNN网络模型的训练,10%作为网络模型的测试集,验证训练后的模型预测的准确度。在每一次迭代,学习率进行动态更新。设置初始学习率为0.001,每20个epoch都对当前的学习率根据设置的衰减因子lr=0.75进行衰减。

在区域分类器的数据集中,对每一个用户,在信噪比为10 dB时使用LS算法估计信道标签。针对训练后的模型,用生成的10 000个样本进行区域划分的准确度进行预测。训练参数设置如表2所示。

表2 训练参数设置Tab.2 Training parameter setting

3.2 仿真结果

对6种下行信道估计方案进行比较：方案1,采用针对区域1的用户训练完成的模型;方案2,采用针对区域2的用户训练完成的模型;方案3,采用针对区域3的用户训练完成的模型;方案4,采用本文提出的基于区域切换的DML分层模型SHDCE方案;方案5,采用LS算法进行信道估计;方案6,采用NMSE算法进行信道估计。

在上述方案中,方案1～4的导频开销为Q1=NM/8=128,而方案5和6的导频开销为Q2=NM=1 024。由此可见,引入分布式机器学习大大减少了信道估计的导频开销。

图4(a)和(b)显示了上述方案在瑞利衰落信道上不同信噪比下的NMSE对比。在图4(a)中,采用通道区域1的数据集作为测试数据。从图4(a)可知,相比于传统的LS算法[6]和NMSE算法[7],机器学习的引入大大提升了信道估计性能。而本文提出的基于分布式机器学习的区域切换模型相比于只针对一个场景下训练的CNN网络的NMSE更低,性能更好。在图4(b)中,对整个区域的所有信道场景随机生成测试样本,可以看出,在信道场景随机的情况下,本文提出的模型更加具有优势,可以获得更好的信道估计性能。

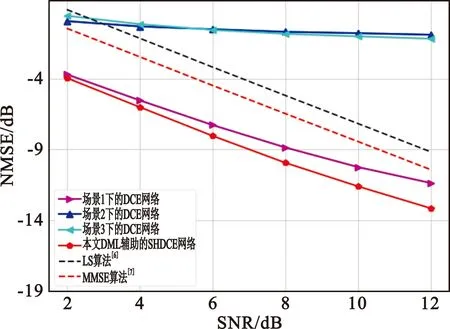
(a)区域1

图5(a)和(b)进一步验证了本文提出的模型在DeepMIMO数据集上性能估计的优势。图5(a)中所有样本集来自于区域1,图5(b)中样本数据集分别来自3个不同区域。从仿真结果可以看出,当移动用户从一个区域切换到另一个区域时,提出的系统模型依旧可以准确地估计用户的信道,可以实时地根据用户所处位置进行相应的信道估计。

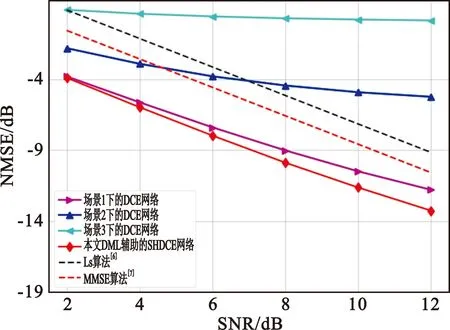
(a)区域1

图6和图7是分别在瑞利衰落信道数据集和DeepMIMO数据集下,采用信道数量为5时训练的SHDCH模型,用于测试所提模型的抗干扰性能。从图6和图7中可以看出,在低信噪比的情况下,不同信道数的NMSE性能基本一致,仅在高信噪比的条件下略有差别。故即使在信道数量变化的环境下,本文提出的模型依然可以达到较高的准确率。

图6 瑞利衰落信道模型中不同信道数的NMSE性能比较Fig.6 NMSE comparison for different number of channels in Rayleigh fading channel model

图7 DeepMIMO数据集中不同信道数的NMSE性能比较Fig.7 NMSE comparison for different number of channels in DeepMIMO dataset

图8对不同信噪比下模型预估的准确率进行了对比。从仿真结果可以看出,在瑞利衰落的信道下估计的准确率明显高于DeepMIMO数据集中的准确率,这是因为DeepMIMO的区域数据集的划分是根据行数进行的,相邻区域数据集有类似的情况。在5 dB的条件下,在瑞利衰落信道数据集中模型估计的准确率为0.90,DeepMIMO数据集中估计的准确率为0.86;而在15 dB的条件下在,瑞利衰落信道数据集估计的准确率达到了0.99,在DeepMIMO数据集中估计的准确率达到了0.96。可以看出模型预估准确率随着信噪比的升高在不断增加,直至在15 dB达到峰值后稳定下来,不再随着信噪比的增加而增加。实验结果表明,信噪比的提升对模型的准确率在一定范围内有提高,但是在高信噪比的条件下提升不大。

图8 不同信噪比下模型预估准确率比较Fig.8 Prediction accuray comparison of the proposed model at different SNRs

3.3 模型复杂度分析

针对本文提出的基于区域切换的DML神经网络模型,复杂度主要包括特征提取器的复杂度以及特征映射器的复杂度。对于卷积层,其复杂度表示为O(E1E2F2CinCout)[19],E1和E2表示每个输出特征的行数和列数,F表示滤波器的边长。对于线性层,计算复杂度为O(L1L2),L1和L2分别表示输入输出的维数。

对于区域分类器设计的CNN网络,其复杂度可表示为O(44400Q1Q2+48Q1QNM);对于特征提取器和特征映射器设计的CNN网络,其复杂度为O(6101.875Q1Q2)。

4 结 论

本文基于DML,针对现有机器学习辅助无线通信系统中出现的通信开销大以及信道估计不准确的问题提出了一种基于区域交集切换的分布式机器学习模型,采用分层次神经网络模型以及区域融合技术对不同区域的信道进行相应的信道模型构建,对处于不同位置的移动用户能够灵活采用对应的信道估计模型,有效提高了信道估计的准确度。同时,由于模型训练部分是在本地服务器上进行,仅需要与中心服务器进行相关梯度向量的传递,有效减少了中心服务器的通信开销。仿真结果表明,本文提出的基于分布式机器学习区域交集模型比基于单用户训练的模型信道估计有更高的准确度以及更好的实用性。