一种基于多重同步压缩的高动态信号捕获技术

程凌峰,倪淑燕,陈世淼,廖育荣

(航天工程大学 a.研究生院;b.电子与光学工程系,北京 101416)

0 引 言

近几年来,Starlink、OneWeb等低轨互联网星座快速发展,已经成为一种新型通信方式,具有广泛的应用前景。对于飞机、导弹等用户,由于低轨卫星高速运动,终端也在高动态运动,在这种情况下接收信号受到较强多普勒效应的影响[1],体现为较大的多普勒频偏及高阶频偏变化率[2]。由于卫星轨道可预报,因此由卫星运动引起的多普勒频移可进行预补偿。但终端动态性引起的多普勒频移则需要利用接收机进行捕获,当接收信号时间内频偏变化超出快速傅里叶变换(Fast Fourier Transform,FFT)分辨率的情况下,传统捕获方法[3-4]难以对信号进行有效的估计。

通信系统在设计帧结构的时候,通常在每一帧的最前端添加导频序列用于捕获,该序列在经过高动态信道之后变为调频信号。目前针对调频信号的参数估计方法主要有两类：参数域类方法和时频分析法。参数域类方法比较常用的有调频率逼近法[5-6]和降阶类参数估计算法[7-8],调频率逼近法对线性调频信号有较好的估计性能,但难以兼顾精度与复杂度,且不适用于高阶调频信号;降阶类参数估计算法可用于非线性调频信号,但是存在高阶参数估计量对低阶参数估计时误差积累的问题,同时可能存在伪峰,抗噪性较差。时频分析法是分析非平稳信号的理想工具[9],它对信号进行时域和频域联合分析获得时频图,通过提取时频图脊线即瞬时频率(Instantaneous Frequency,IF)实现对频率的粗估,如文献[10]就利用分数阶傅里叶变换实现了对线性调频信号的频率估计。对于高阶调频信号的估计,过去通常使用短时傅里叶变换和小波变换,但是受到海森堡(Heisenberg)测不准原理的限制[11],其时频分布是模糊的,不利于脊线的提取。为了提高传统方法的能力,近几十年来学者们提出了时频重排(Reassignment Method,RM)[12]、同步压缩(Synchrosqueezing Transform,SST)[13]、高阶同步压缩(High-Order Synchro Squeezing Transform,HOSST)[14]和同步提取变换(Synchro Extracting Transform,SET)[15]等方法。时频重排法具有较好的时频聚集能力,但是无法实现信号重构;同步压缩法对快时变信号的聚集能力较差,存在频率估计误差逐步增大的问题;高阶同步压缩对噪声鲁棒性较差,低信噪比下时频图发散严重;同步提取变换方法是短时傅里叶变换的后处理形式,去除大部分时频点,提高时频能量聚集度,在重构信号时减少了计算量,但是存在对快时变信号鲁棒性较差的问题[16]。

针对以上问题,本文根据高动态信号特点将其建模为非线性调频信号,并提出一种基于多重同步压缩(Multisynchro Squeezing Transform,MSST)的时频分析法提高时频聚焦能力。在此基础上对传统脊线提取方法进行了改进,设计了一种分段能量泛函最小化法,解决了由于噪声导致的提取点错误问题,提高低信噪比下信号估计能力。

1 高动态信号建模

发射信号经过信道传输进入接收机,并经过自动增益控制、下变频和匹配滤波后,进入载波同步。信号模型可表示为

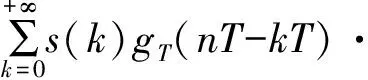
(1)

式中：s(k)表示调制数据,k为整数;gT(t)为信号成形滤波器的冲激响应;T为符号周期;Δf和Δθ为接收机接收到的信号载波频率、载波相位与本地载波频率、相位的差值;w(nT)是均值为0的高斯白噪声。

导频序列通常为无数据变化的常数序列：

s(k)=1,k=0,1,…,P-1

(2)

式中：P为导频长。

暂不考虑成形滤波器的拖尾,则经过下变频和滤波后的基带信号可表示为

(3)

受相对速度和相对速度变化率等的影响,可将时变基带信号相位近似高阶泰勒级数展开：

(4)

式中：f0,f1,f2分别为频偏、一阶频偏变化率和二阶频偏变化率。再考虑到导频数据较短的情况,忽略了更高阶频偏变化率分量造成的影响,从而载波捕获的问题转换为非线性调频信号的参数估计问题。

2 基于多重同步压缩的高动态信号时频分析

2.1 同步压缩基本原理

同步压缩是基于短时傅里叶变换(Short Time Fourier Transform,STFT)进行后处理得到的。对于信号r(t),STFT可表示为

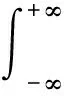
(5)

式中：g(t)为窗函数;r(t)为输入信号。受到海森堡测不准原理的制约,STFT无法同时实现时频的高分辨率。SST方法实际上是对STFT在频率方向进行能量重新分配的一种方法,如图1所示,主要用于纯谐波信号分析,其过程可以表示为[17]

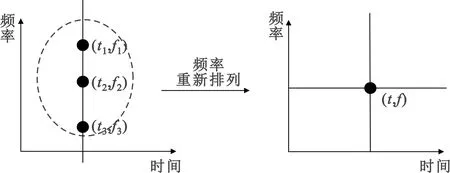
图1 同步压缩方法时频能量分配Fig.1 Time-frequency energy distribution using synchronous compression method

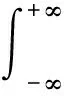
(6)

接收信号的SST表达式为

(7)

(8)

(9)

2.2 高动态信号的同步压缩

对于本文研究的高动态信号,由于STFT的窗函数较短,二阶频偏变化率影响较小,因此可以将其所加窗内信号近似为线性调频信号,即

r(τ)=Aej[φ(t)+2πf0(τ-t)+πf1(τ-t)2]

(10)

同时,定义窗函数为高斯窗g(t)=e-0.5t2,则

(11)

(12)

因此将式(12)两边对时间求偏导可得

(13)

因为式(13)是复数形式,不能直接用于计算,取实部可得

(14)

2.3 高动态信号的多重同步压缩

为了提高处理快时变信号时的频率分辨率,前人通过采用高阶的同步压缩方法以应对多阶的瞬时频率,但是高阶同步压缩在较低信噪比环境下性能恶化严重。为此,本文设计了一种高动态信号的多重同步压缩方法。

(15)

进一步可得

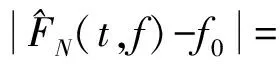
(16)

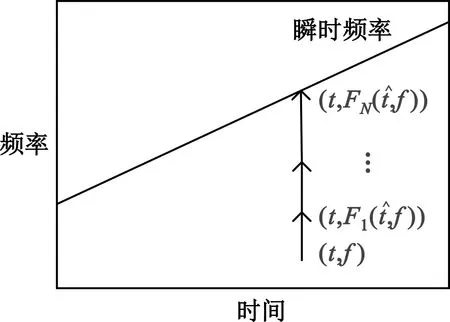
图2 MSST频率压缩过程Fig.2 MSST frequency compression process

(17)

(18)

经过多次迭代,模糊的STFT时频分布能量得到集中,瞬时频率的估计会越来越接近信号的真实频率,在脊线提取环节就会获得更为准确的瞬时频率脊线,提高参数估计精度。

3 基于分段能量泛函最小化的瞬时频率估计

时频分析为信号参数估计提供了有力的工具,瞬时频率作为信号的重要物理量,其从时频图提取的准确性对非平稳信号的研究具有重要的意义。基于时频分析的瞬时频率提取方法有很多,如谱峰检测法[18]、能量泛函最小化法[19]等。谱峰检测法在高信噪比环境下性能较好,但是低信噪比下噪声会导致时频图谱峰点的偏移,造成较大误差。

3.1 能量泛函最小化法

能量泛函最小化法对信号时频分析的结果增加惩罚函数,选取匹配参数,计算出使得曲线平滑且能量最大的瞬时频率曲线。其计算公式为

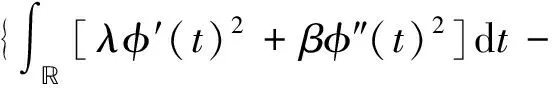
(19)

式中：λ和β是调整正则化水平的两个参数。通过式(19)可以看出,时频因子的能量以及提取瞬时频率的平滑度都是要被考虑的因素。文献[20]中提出的瞬时频率提取算法的起始点选择为全域最大值,这种方法的优点是可以明显减小计算量,但是在某些情况下不能保证全局最大值精确地位于真实的瞬时频率上,这就偏离了式(19)的初衷,如异常情况引起的较大波动或者信噪比较低时导致的不正确起始点。

3.2 分段能量泛函最小化法

为了提高瞬时频率提取过程的效率和可靠性,考虑将整个时频平面分割成几个区段。具体步骤如下：将给定的时频平面Ts(h,m)分为F个部分,设置最大容许频率变化为Δ,数据长度为L。对划分的时频平面依次分段确定起始点,并进行前向后向同时搜索瞬时频率脊线,最后根据时频能量从这些轨迹中选出最佳的瞬时频率轨迹。

结合时频分析和频率提取过程,高动态载波频率捕获算法的整体流程如图3所示。

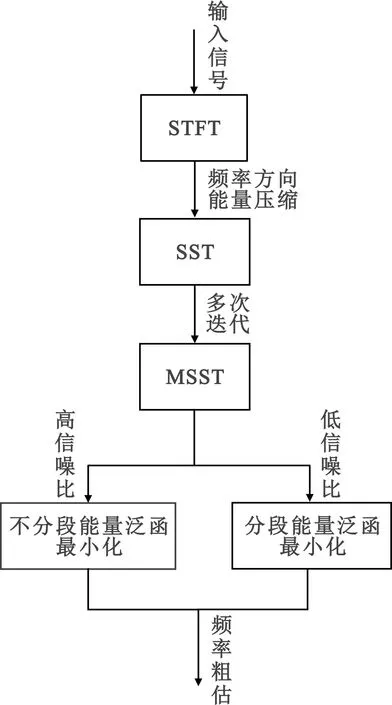
图3 高动态捕获方法流程Fig.3 Flowchart of high dynamic aquisition method

4 性能仿真分析

4.1 仿真条件

由于卫星运动轨道确定,因此由卫星运动造成的多普勒频移一般会采用预补偿方式,高动态性主要考虑由终端引起的。美国JPL提出了一种具有典型性的高动态模型,假设飞行器运动速度最大为2 km/s(6Ma),加速度最大为400 m/s2(40g),加加速度最大为1 000 m/s3(100g/s)。将接收信号建模为二阶非线性调频信号,按移动卫星通信常采用的S频段(3 GHz)计算,多普勒频移范围±20 kHz,变化率范围±4 kHz/s,二阶变化率范围±10 kHz/s2。采样频率设为fs=50 kHz,数据长度N=5 000。频偏、一阶调频率、二阶调频率在取值范围内随机取值,在计算频率估计均方根误差和捕获概率时采用500次蒙特卡罗仿真,比较STFT、RM、SST、SST3、SET和MSST这几种时频分析方法在高动态非线性调频信号参数估计中的性能。其中,SST3表示三阶同步压缩方法(Third-order Synchro Squeezing Transform),是高阶同步压缩的典型方式。

4.2 迭代次数的确定

作为一种迭代算法,需要确定MSST迭代终止的条件。本文采用时频分析瑞利熵和重构信号的信噪比变化来确定合适的迭代次数。

时频聚集性是时频分析方法性能优劣的重要指标之一,通过将时频分析和信息熵结合,提出利用瑞利熵来表征时频分析方法性能。α阶瑞利熵的定义为[21]

(20)

Ryα越小,时频聚集程度越高。瑞利熵可以确保MSST时频聚集到合适的水平,当迭代过程中连续时频分析结果的瑞利熵没有明显的变化时,迭代过程可以中止。

对时频分析结果进行重构,比较不同迭代次数重构后信号的信噪比,如果相邻两次信噪比不再明显变化,迭代过程可以中止。图4和图5分别为迭代次数对瑞利熵和重构的影响,可以看出,迭代次数越多,瑞利熵越小,重构后的信号信噪比越高,经过3次迭代,瑞利熵和信噪比趋于稳定。除了MSST的重构信噪比外,图5中还给出了STFT、SST、SST3和SET的重构信噪比,输入信噪比为5 dB。可以看出,除MSST外其他几种后处理方法都会实现一定的信噪比提升,但是STFT重构时会降低信噪比。SST略有提升(MSST一次迭代时),SST3大约提升4 dB,SET提升约6 dB,而MSST在稳定后信噪比提升了约9 dB,性能提升非常明显,这证明了后处理技术的优势。MSST的这种能力可以考虑用于信号的信噪比增强。

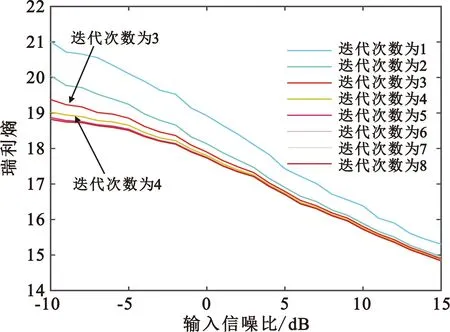
图4 迭代次数对瑞利熵的影响Fig.4 Influence of iteration times on Rayleigh entropy

图5 迭代次数对重构信噪比的影响Fig.5 Influence of iteration times on the reconstruction signal-to-noise ratio

4.3 时频聚集能力

假设信号信噪比为5 dB,STFT、RM、SST、SST3、SET和MSST这6种方法的时频二维能量分布如图6所示,其中右侧为时频分析局部放大图。对除了STFT之外的时频图采用统一刻度进行比较可以看出,STFT的能量聚集最差,局部放大后几乎难以分辨脊线;SST的瞬时频率受到估计模型和噪声的限制,时频发散,时频点能量较低;RM方法由于是从时间和频率两个方向重新分配时频能量,因此得到了比SST更集中的时频图,但放大后时频图的脊线还是处于发散状态;SST3虽然是针对二阶非线性调频信号设计,相对于SST方法模型更为准确,但是在较低信噪比下性能欠佳,时频图较为发散;SET方法通过去除模糊的时频点实现能量集聚,在某些时段聚集性能优于MSST,但由于对快时变的鲁棒性欠佳,在时频线的交界处能量断层且在噪声的影响下时频线出现上下波动的现象,造成估计误差增大;MSST实现了最集中的时频分析结果,能够看到清楚的时频图脊线,为后续提取脊线进行准确瞬时频率估计提供了保证。

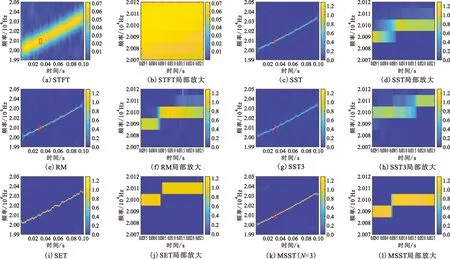
图6 不同时频分析方法分析结果及局部放大图Fig.6 Analysis results and local magnified images using different time-frequency analysis methods

用瑞利熵对6种方法的性能进行定量分析,结果如图7所示。可以看出,输入信噪比在-10～15 dB时,MSST算法的瑞利熵远小于其他几种方法,这也证明了在几种方法中MSST的时频聚焦能力最优。

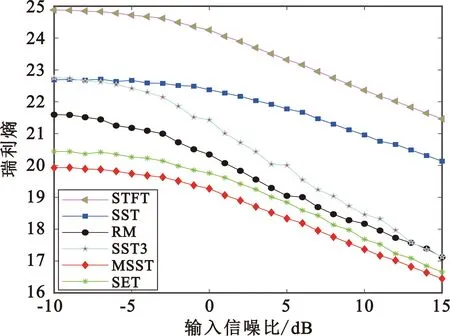
图7 不同时频分析方法的瑞利熵随信噪比变化情况Fig.7 Variation of Rayleigh entropy with signal-to-noise ratio using different time-frequency analysis methods

4.4 频率估计精度

图8为不同方法的频率估计均方根误差随信噪比变化情况,可见MSST方法的频率估计均方根误差始终是最小的,在较高信噪比(大于10 dB)时,各个方法的均方根误差变化趋于平稳,MSST方法的均方根误差约为STFT方法的1/3,且均方根误差大小与时频聚集能力成负相关。在较低信噪比(小于0 dB)时,虽然MSST的均方根误差依然是最小的,但是其他5种方法的均方根误差不是完全按照时频聚集能力的顺序排列的,这说明作为STFT的后处理方法,不仅将有用信号的瞬时频率时频能量聚集,同时也会将噪声聚集,在瞬时频率估计的时候造成过大的误差。很明显,MSST对信号的时频聚集能力强于噪声聚集能力,而SST、RM和SST3在低信噪比时瞬时频率的时频能量严重发散,无法实现准确地瞬时频率估计,甚至相较于STFT的估计精度都出现下滑,其中SST3的频率估计误差在信噪比-1 dB以下保持在高位,噪声鲁棒性较差,但是随着信噪比的提升,SST3能够准确分析快时变信号的能力逐渐突显,在较高信噪比下频率估计误差仅次于MSST。SET方法在较低信噪比时频率估计性能较好,但是在高信噪比时仅略优于STFT,性能整体表现平稳。MSST的这个特性对于在较低信噪比下的载波捕获有重要的意义。本文中分段能量泛函最小化法的分段数取为400。由图8可知,信噪比在-5 dB以下时分段意义重大,即使是MSST方法,在这种很低的信噪比下如果不分段频率估计性能下滑都极其严重,在-10 dB时频率估计均方根误差增大了近10倍,在-5 dB以上分段与否对性能影响很小,可以根据实际应用场景选择合理的分段数实现精度和运算量的平衡。

4.5 捕获概率与时间

图9比较了不同算法的捕获概率。捕获概率通常定义为信号频率估计误差小于20 Hz的概率。MSST方法在捕获概率收敛后可达到99%,且在低信噪比条件下仍能保持95%以上,明显优于其他方法。同时也能发现SST、RM、SST3和SET这4种方法在高信噪比条件下捕获概率均收敛到95%以上,而STFT的捕获概率收敛到80%左右,也证明了对STFT后处理的必要性。同样也可以发现,在-6 dB以下频率估计时不分段的缺点逐渐明显,在-10 dB时MSST法的捕获概率降到90%以下。

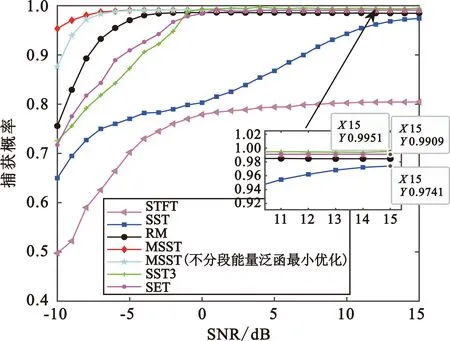
图9 不同方法捕获概率随信噪比变化情况Fig.9 Variation of aequisition probability with signal-to-noise ratio using different methods

在实际应用时,时频分析方法的运行效率非常关键,这决定了其能否应用于实际工程中。假设时间点数和频率点数分别为Nt和Nf,STFT的时间计算复杂度为O(NtNflb(Nf),后处理方法的多重压缩、求导及重新分配时频能量等步骤的计算复杂度为低阶项,可忽略。采用测试的计算机配置为i7-10750H 2.6 GHz,Win10系统,Matlab版本为R2020a。所需时间如表1所示,所有方法都在15 s内完成处理。MSST相对于SST方法时间增加较少,且随着迭代次数的大幅增加,MSST方法所需计算时间增加幅度不大,即使选择了较大的迭代次数,MSST方法的计算时间仍明显小于SST3,具有较好的实际使用价值。

表1 不同时频分析方法所需计算时间Tab.1 Calculation time required for different time-frequency analysis methods

5 结束语

本文针对传统的时频图频率估计方法起始点选取错误导致脊线提取异常的问题,提出在时频平面上分段选取起始点,前向后向同时搜索,独立提取脊线,提高频率估计准确度。在高信噪比条件下频率估计均方根误差趋于收敛时,MSST方法的均方根误差约为STFT和SET的1/3,为SST、RM和SST3等后处理方法的1/2,捕获概率为99%以上,且在低信噪比条件下,MSST的频率估计性能波动不大,捕获概率为95%以上,取得了较好捕获效果。同时,在确定MSST最佳迭代次数时发现,MSST存在提升重构信号信噪比的能力,也为增强信号提供了一种思路,提高了MSST的实用性。

MSST方法是在SST方法框架下的方法,SST方法是假设所取窗内信号为单频谐波信号,虽然通过多步压缩提高时频聚集度,但在本文场景下还是会导致频率估计误差随时间积累。SST3是一种很好地技术,它就是针对信号是二阶非线性调频信号的基础上,但是受制于本身较差的噪声鲁棒性,在较低信噪比条件下性能很差,后续可以尝试对其改进用于信号捕获。