基于Kraljic矩阵和PCA算法的手术器械分类管理研究

朱梦滢，杨思悦，罗冰洁，吴晓东

四川大学华西医院 设备物资部，四川 成都 610041

引言

本文讨论的手术器械指重复使用手术器械，根据2015 年出台的《医疗器械分类规则》[1]，重复使用手术器械指用于手术中进行切、割、钻、锯、抓、刮、钳、抽、夹等过程，不连接任何有源医疗器械，通过一定的处理可以重新使用的无源医疗器械。目前与手术器械相关的管理研究主要集中在优化消毒供应管理方面[2-3]，而在手术器械物流管理方面，大部分医疗机构采取相关手术室自行管理的方式，主观性较强，且由于物流管理数据没有实现线上化，缺乏系统化的数据管理，无法从数据中获取优化管理的办法。此外，与医用耗材管理不同，手术器械管理流程中有消毒供应环节，每次使用前需要经过严格的清洗、消毒、干燥、无菌存放，因此很难像医用耗材一样通过在外包装上张贴射频识别标签[4-5]、二维码[6-7]等方式借助物联网手段进行物流管理。有文献提到以表面喷涂二维码的方式对价值极高的达芬奇机器人手术器械进行管理[8]，这种方式成本很高，仅适合极少数高值手术器械。部分文献中提到运用ABC 分类法对手术器械进行分类管理[9-11]，该方法从经济价值的角度去判断物资的重要性，并对A 类物资进行重点管理。在实际的手术器械物流管理中，除器械自身经济价值外，器械的市场供应风险也是管理关键点。因为一旦器械发生缺货，就会影响临床手术的开展。Kraljic 矩阵是物流管理中常用的工具，它能从物资的经济价值和市场供应的复杂程度两个维度去评价物资的重要性[12-13]。本文结合Kraljic 矩阵思维，构建贴合手术器械物流管理特征的分类指标体系，并引入主成分分析（Principal Component Analysis，PCA）算法结合Kraljic 二维矩阵对手术器械进行分类，给出相应的物流管理策略。这种分类方式对手术器械的物流管理具有实操意义，既保留了手术器械特征信息的多样性，又能以简明科学的方式对不同类型的手术器械制定不同的物流管理策略，解决了手术器械管理主观性强、缺乏对市场供应风险的考虑的问题。

1 资料与方法

本文选取H 医院2021 年耳鼻喉科手术器械的出库数据进行研究，共计151 种手术器械，分别由12 家供应商供货。

1.1 基于Kraljic矩阵的手术器械分类指标体系构建

手术器械品类繁杂，需要构建一个科学合理的分类指标体系，对不同器械分类管理。本文手术器械分类指标体系基于Kraljic 矩阵构建，见图1，从物资自身价值和市场供应风险两个方面，将物资分为战略类物资、杠杆类物资、瓶颈类物资和常规物资4 类。本文将基于Kraljic 矩阵，从手术器械的经济价值维度和市场供应风险维度选取具体的指标构建手术器械分类指标体系。

图1 基于Kraljic矩阵的物资分类

在经济价值维度中，使用ABC 分类法衡量手术器械经济价值。ABC 分类法常应用于库存管理[14]，将物资品类数占全部品类数比例5%～15%，且金额占总金额比例60%～80%的物资分类为A 类物资；将品类数占全部品类数比例20%～30%，且金额占总金额比例20%～30%的物资分类为B 类物资；将品类数占全部品类数比例60%～80%，且金额占总金额比例5%～15%的物资分类为C 类物资。此外，为了更好地量化不同类型手术器械的经济价值，结合手术器械管理经验，对ABC 类手术器械分别赋值，手术器械经济价值越高，赋值越大。

在市场供应风险维度中，结合历史文献中评价物资供应风险采取的评价方法[15-16]，和手术器械管理涉及的道德各环节所关注的市场供应风险关键指标，分别从手术器械自身属性和供应商因素两个方面构建手术器械的市场供应风险评价指标。此外，结合领域经验和历史文献中对评价指标的量化方法，根据手术器械在每个指标存在的水平差异，对不同指标下的不同手术器械赋值。其中，赋值越大代表该指标下该器械的市场供应风险越大。

1.2 PCA算法

丰富的指标特征维度可以更加全面地评价物资的重要性，但同时过多的维度也会增加分类的复杂性，且某些指标间可能存在相关性。为了将构建的指标体系降到二维平面中，本文使用PCA 算法对数据进行处理。PCA 利用正交变换把原有n维特征转换为k维线性不相关的新变量，这些新变量也称为主成分，从而利用主成分在更小的维度下展示数据特征。本文使用的数据样本大小为151，根据构建分类指标体系生成10 维指标特征，构成一个151×10 阶矩阵X，每个矩阵元素为Xm,n。由于10 个指标特征量纲不一，需要对数据进行预处理。使用归一化方法将数据缩放为在[0，1]间的数值，归一化计算方式如公式（1）所示。

对协方差矩阵C 做对角化处理，将除对角线外的其他元素转化为0，即寻找一个矩阵P，满足PCPT是一个对角矩阵，且对角元素λn按降序排列，见公式（3）。此时对角元素λn为各特征向量的特征值。

确定降维维数k，用P 的前k行组成的矩阵乘以原始数据矩阵X，即可将原始数据降至k维。

2 结果

2.1 手术器械分类指标体系

本文基于Kraljic 矩阵思维，从经济价值和市场供应风险两个角度出发，构建了手术器械分类指标体系，见图2。

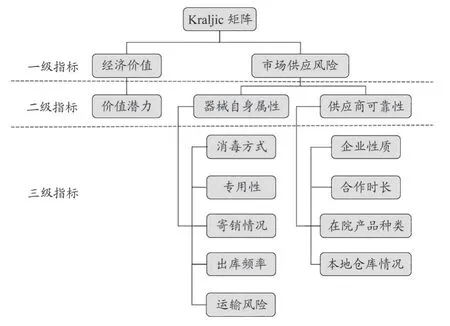
图2 基于Kraljic矩阵的手术器械分类指标体系

在经济价值维度，使用ABC 分类法对手术器械进行分类来评估不同器械的价值潜力，分类结果如表1 所示。其中，A 类器械经济价值最高，B 类次之，C 类最低。

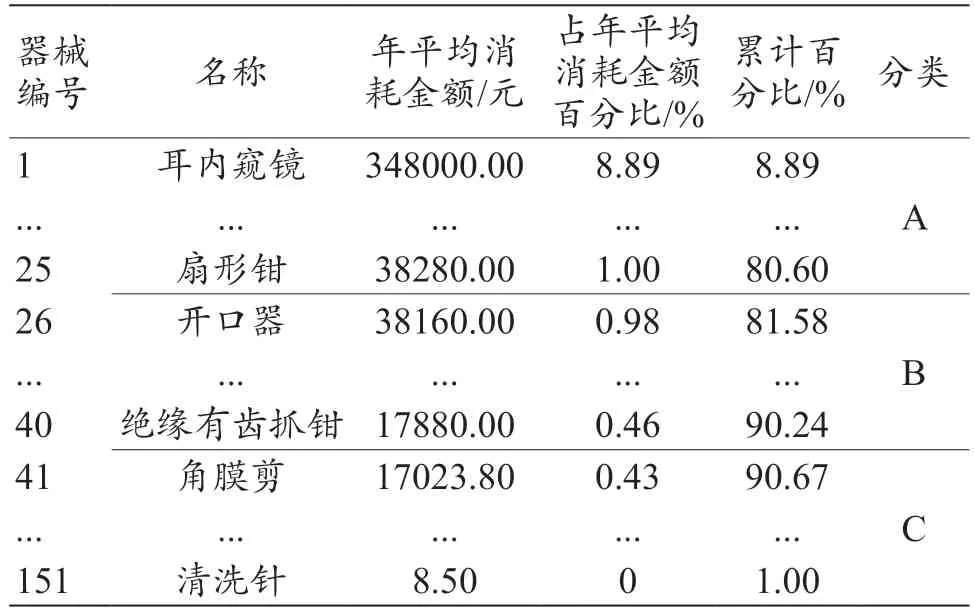
表1 手术器械ABC分类结果

在市场供应风险维度上，结合参考文献[15-16]，从手术器械全生命周期涉及的环节——供应商、采购维修部门、消毒供应中心和临床使用部门的角度出发，收集其关注的市场供应风险关键指标，选取可量化、可获得的指标。最终手术器械分类指标及赋值如表2 所示。

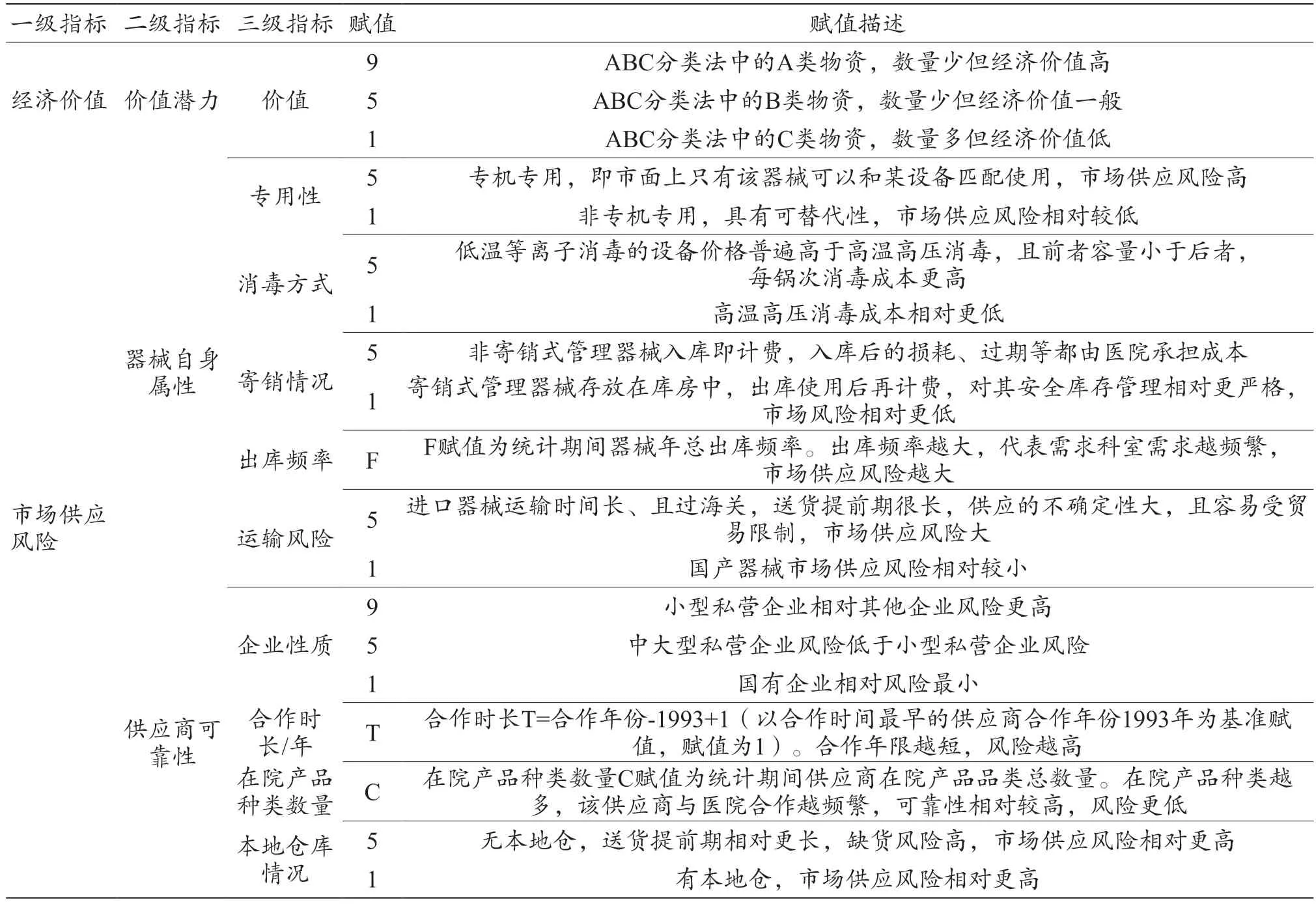
表2 手术器械分类指标赋值及描述

由于在PCA 降维前会使用归一化方法将不同手术器械在不同指标上的赋值缩放为[0，1]间的数值，具体计算见式（1），相较于赋值绝对值大小，本文更关注的是不同类型手术器械在该指标下赋值的相对差异。计算可知，当一个指标只有两种可能值，归一化之后会变成0 或1；当一个从指标只有3 种可能值，归一化后会变成0、0.5、1.0；当指标值如“合作时长”指标、“在院产品种类数量”指标的值有多种可能，归一化后也会变为[0，1]间不同数值。根据表2 构建的手术器械分类指标体系，量化统计期内151 件手术器械的特征指标，生成特征数据如表3 所示。此时，各指标的量纲不统一，因此各指标间差异很大。

表3 手术器械在不同指标下的量化结果

2.2 PCA结果

为了降低特征数据的复杂度，便于在低维空间中对数据进行可视化，更好地观察手术器械的分布情况，使用PCA 算法对特征数据进行降维。使用归一化方法去量纲后，从10 个原始特征中提取主成分。

许多PCA 算法中都默认当降维后主成分的累积贡献率达到95%时降维进程终止，一些文献[17-18]中也提取了累积贡献率为95%的主成分来实现数据降维。然而，根据Jackson[19]的研究，将主成分累积贡献率固定为95%是不合理的，实际应用中不同场景累积贡献率的设置差异很大。在本文中，累积贡献率前95%的主成分其贡献率和累积贡献率如表4 所示。其中，主成分1 的贡献率占40%以上，提取2 个主成分累积贡献率接近80%，而需要提取7 个主成分累积贡献率才能达到95%。显然，在原始数据特征数量为10 的情况下，提取2 个主成分就能解释80%左右的变量是优于提取7 个主成分才能解释95%的变量的。因此本文提取2 个主成分，将多维数据降为二维数据，也便在低维空间中观察手术器械分布。

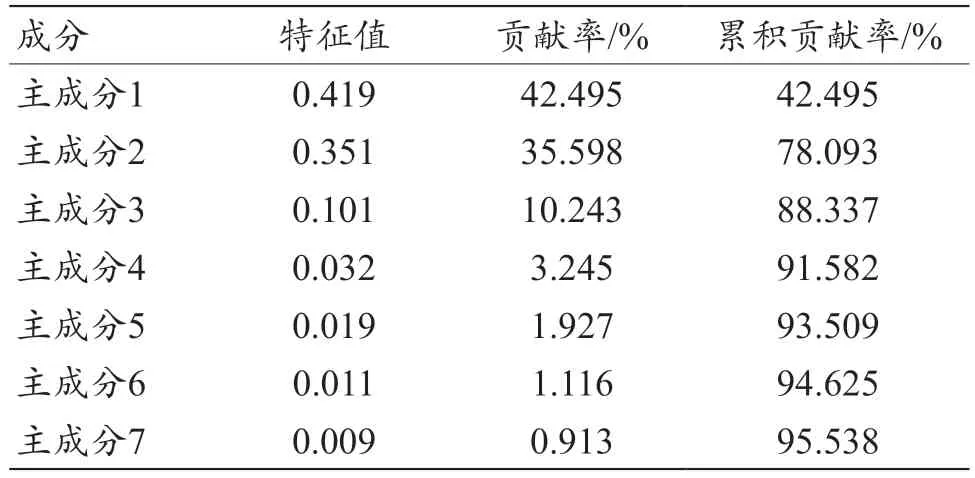
表4 PCA算法中前7个主成分信息

2.3 基于Kraljic矩阵的手术器械分类结果及分类管理方法

使用PCA 算法提取2 个主成分的过程实际上是将原始指标的10 维空间变量坐标系沿着综合方差最大的两个方向重建为二维空间坐标系。设原始坐标轴中的某个点为X（x0，...，x9），该点映射到新的坐标系的坐标Y（y0，y1），表5 则是PCA 算法输出的变换矩阵W 的转置矩阵。其中，X1到X10是原10 维空间，表内的数值是原10 维空间经PCA 转换后对应的新维度所占权重。WT*X 就是将原始坐标系中的点转化到新的坐标系。根据变换矩阵可知，新坐标系的第1 维主要受旧坐标系的第1 维（价值潜力指标）影响，新坐标系的第2 维几乎不受旧坐标轴的第1 维影响。

表5 变换矩阵的转置矩阵WT

此外，将主成分1 作为x轴，将主成分2 作为y轴，将绘制出如图3 所示的手术器械分布图，从而将所有器械展示在二维平面中。图中分别用红色圆形、绿色三角形和蓝色正方形代表ABC 三类手术器械，颜色越深代表该处重叠的手术器械越多。观察ABC 类器械的分布，首先从主成分1 表示的x轴看，经济价值较高的A 类手术器械主要集中在x轴右侧，经济价值较低的B、C 类手术器械主要集中在轴左侧（尤其是x轴下方区域右侧全为A 类器械，x轴下方区域左中区域全为B 类器械，x轴下方区域最左侧全为C 类器械），手术器械经济价值呈现出沿x轴从左向右逐增的趋势，说明主成分1 表示的x轴很大部分是经济价值的表达，且经济价值沿x轴右侧逐渐递增；从主成分2 表示的y轴看，ABC 三类器械均匀分布在纵向方向上，也侧面说明主成分2 中经济价值几乎没有表达。

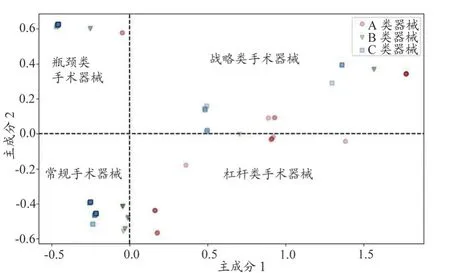
图3 手术器械分布图

根据以上分析，主成分1 主要受经济价值影响，而主成分2 中几乎没有经济价值的表达，结合1.1 中指标特征的选取主要来源于经济价值方面和市场供应风险方面可知，主成分2 主要受市场供应风险的影响。因此，图3 中主成分1 代表图1 中Kraljic 矩阵的物资价值，＞0代表经济价值高，＜0 代表经济价值低；图3 中主成分2代表图1 中Kraljic 矩阵的物资市场供应风险，＞0 代表市场供应风险高，＜0 代表市场供应风险低。根据Kraljic矩阵的物资分类方法，图3 将手术器械分为战略类手术器械、杠杆类、瓶颈类和常规手术器械。其中战略类手术器械22 件，杠杆类手术器械15 件，瓶颈类手术器械46 件，常规手术器械68 件。

对手术器械进行分类后，采用不同的管理方法对4 种不同类型的手术器械进行管理。对于高价值高风险的战略类手术器械，由于其市场供应紧张，应与供应商建立相对信任的长期合作关系，重点管理该类器械。内部管理中，可以探索该类手术器械寄销管理模式，提前备货，使用后结算，尽量缩短该类器械的订货提前期、减少资金占用；同时定期调研该类手术器械的临床使用满意度，并向供应商反馈，提升其服务水平。外部管理中，可以要求供应商提高该类手术器械的备货量，降低缺货风险。

对高价值低风险的杠杆类手术器械，由于其在市场上有充足的供应商资源，竞争激烈，管理上应更注重规模与效率。可以探索多家供应商作为该类器械的购买来源，设计合理的规则，综合供应商的价格水平和服务水平，并据此对不同供应商分配不同数量的订单。价格最低、服务最佳的供应商可获得最多订单，以此保持供应商间的充分竞争。

对低价值高风险的瓶颈类手术器械，管理策略是保持稳定持续的供应，保证订货后的按时交付。对这类器械的管理，需要仔细梳理风险存在的原因，从根本上降低风险。同时，此类器械金额较小，对供应商的吸引力不大，需要库房备有足够的安全库存，并主动为供应商及时供货创造条件与提供便利，保持与供应商友好的关系。

对低价值低风险的常规手术器械，管理策略是降低管理成本。这类器械一般存在品类繁杂、每类数量不多、价值不高的情况，很容易花费大量的管理时间。因此，可以将该类器械的整个物流管理流程进行程序化、线上化，能实现批量化的采购订货、库存管理，在不影响交付的前提下减少管理投入时间。

3 讨论与总结

针对手术器械物流管理主观性强、现有管理办法仅考虑手术器械经济价值的问题，本文基于Kraljic 矩阵，结合手术器械全生命周期参与者的领域经验，除经济价值外，增加了对市场供应风险的考量，从这两个维度构建了手术器械管理的评价指标体系。在经济价值维度，本文使用经典的ABC 分类法，对手术器械分类来衡量手术器械的价值潜力；在市场供应风险维度，从器械自身属性方面选取了专用性、消毒方式、寄销情况、出库频率和运输风险5 个指标，从供应商可靠性方面选取了企业性质、合作时长、在院产品种类数量和本地仓库情况4 个指标，全方位衡量手术器械的供应风险。之后，对各指标进行赋值来量化不同手术器械在各个指标下的表现，并使用归一化方法达到统一量纲的目的。此外，使用PCA 算法提取2 个主成分，既能解释大部分的原始变量，又便于在低维空间中观察手术器械的分布。根据PCA 算法输出的变换矩阵及观察以主成分为坐标轴的手术器械分布图可知，主成分1 主要受经济价值影响，主成分2主要受市场供应风险主导。因此，基于Kraljic 矩阵物资分类方法，在以主成分为坐标轴的手术器械分布图中，根据经济价值、市场供应风险的高低可将手术器械分为战略类、杠杆类、瓶颈类和常规手术器械4 类。最后，根据不同类手术器械管理重点提出对应的管理方法。

相比文献[9-11]中常用的ABC 分类管理方法而言，本文提出的基于Kraljic 矩阵和PCA 算法的手术器械分类管理方法除了关注手术器械的经济价值外，还考虑了市场供应风险，方法更完善、考虑更全面。此外，本文选取的评价指标参考了文献[15-16]，同时结合了手术器械全生命周期涉及的各个环节的实践经验，更具有实践指导意义。同时，这种管理方法也基于物流管理中成熟的管理工具Kraljic 矩阵展开，为手术器械物流管理提供了更科学的管理依据。

同时，本文也存在一定局限性。比如，PCA 算法在不满足高斯分布的情况下，得出的主成分可能并不是最优。此外，本文构建的指标体系中各指标都使用归一化的方法来统一量纲，未设计指标权重，后续可以进行更深入的研究，结合实际业务情况设计指标权重来体现不同指标间的重要性差异。