球形敏感单元微瞄准形成金属/空气/金属微观界面中的电子输运机理研究

边星元,赵东方,崔俊宁

(哈尔滨工业大学超精密光电仪器工程研究所,超精密仪器技术及智能化工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150080)

0 引言

惯性陀螺和航空、航天发动机等高端/尖端仪器装备中,关键零部件大量采用深孔、沟槽等内腔体结构。此类结构常与仪器装备的精度等核心性能直接相关,因此在加工制造过程中需进行严格的质量控制,以保证仪器装备高精度等高性能的实现。为满足此类结构的高精度、无损伤和高效率测量需求,兼顾高分辨力、无损伤、高频响、三维各向同性和点瞄准特性的非接触传感方法亟待突破,而其关键在于新传感原理。迅速发展的量子技术,为探索新原理的三维非接触式纳米传感方法提供了新途径;始于扫描隧道探针针尖钝化现象的相关试验性研究,则为本研究指引了新方向。然而,相较于现有基于针尖结构的一维电子隧穿传感方法,将“原子级”尖锐针尖扩展为百微米至毫米直径球形敏感单元,产生传感电流的电子输运机理和模型有待深入研究。因此,展开传感方法研究的基础和前提,是对球形敏感单元瞄准被测面形成的金属/空气/金属微观界面中电子输运的主要机理进行研究。

从绝缘介质薄层电子输运机理和绝缘介质性质改变而产生电子输运两个角度,对包括电子隧穿在内的各种电子输运机理进行形成条件和电流密度特性的分析,阐明微观界面中电子输运的主要机理。

1 微球微瞄准构成的微观界面与传感结构

为满足特种形状和复杂结构高精度测量的迫切需求,研究非接触式传感方法,通过检测电流获取间隙信息,其基本原理示意如图1 所示。在进行非接触式传感时,金属球形敏感单元微瞄准金属被测面,二者间的微小缝隙由空气薄层填充。在构成的金属/空气/金属微观界面加载偏置电压形成偏置电场,该界面中产生电子输运并形成传感电流。实际测试中在百纳米左右的间隙下探测到纳安量级的传感电流。而由于该电流产生条件与传统基于一维电子隧穿原理和尖锐针尖结构的扫描隧道探针传感差别较大,此时传感电流产生的电子输运主要机理是否仍为电子隧穿难以直接确定,传感电流与瞄准间隙的关系尚未得到明确的理论表征。为解决该问题,首先探究微观界面中的电子输运机理。

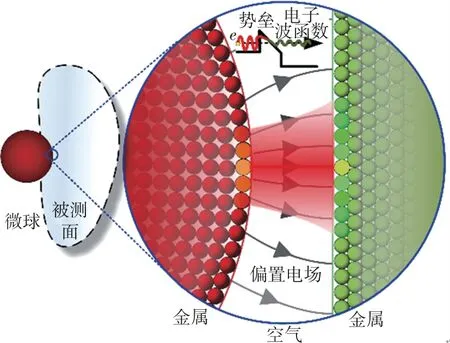
图1 球形敏感单元微瞄准被测面形成的金属/空气/金属微观界面示意图Fig.1 Schematic diagram of the metal/air/metal micro-interface formed by a sphere micro-probing a measured surface

2 微球瞄准微观界面中的电子输运机理研究

2.1 导体/绝缘体/导体微观界面中的电子输运机理

尽管空气在常规条件下是绝缘体,但在导体/绝缘体/导体微观界面加载偏置电压的情况下,包括电子隧穿在内的多种物理机理可致使界面的绝缘层中出现电子输运现象从而产生可探测的微弱电流。而且在实际情况中,多种现象可能同时发生并各自贡献总电流的一部分。为探究其主导机理,从绝缘介质薄层自身的电子输运机理和绝缘介质发生改变而产生电子输运两个角度展开研究。

首先,稳定绝缘介质薄层中电子输运产生的物理机理分为电极限制导电(Electrode-limited Conduction)和体限制导电(Bulk-limited Conduction)两大类。电极限制导电是指导电机理取决于电极和绝缘介质界面的电学特性,形成电流的载流子来源于电极本身,该类机理包括电子隧穿效应和肖特基发射效应(Schottky Emission)。根据发生条件的不同,电子隧穿又可分为直接隧穿效应与福勒-诺德海姆隧穿(Fowler-Nordheim,FN)效应[1]。直接隧穿效应、福勒-诺德海姆隧穿效应和肖特基发射效应的能级示意如图2 所示。针对金属球形敏感单元以亚微米间隙微瞄准金属被测面,在外加偏置电场的条件下产生电子输运现象,首先分析前两种电极限制导电机理。

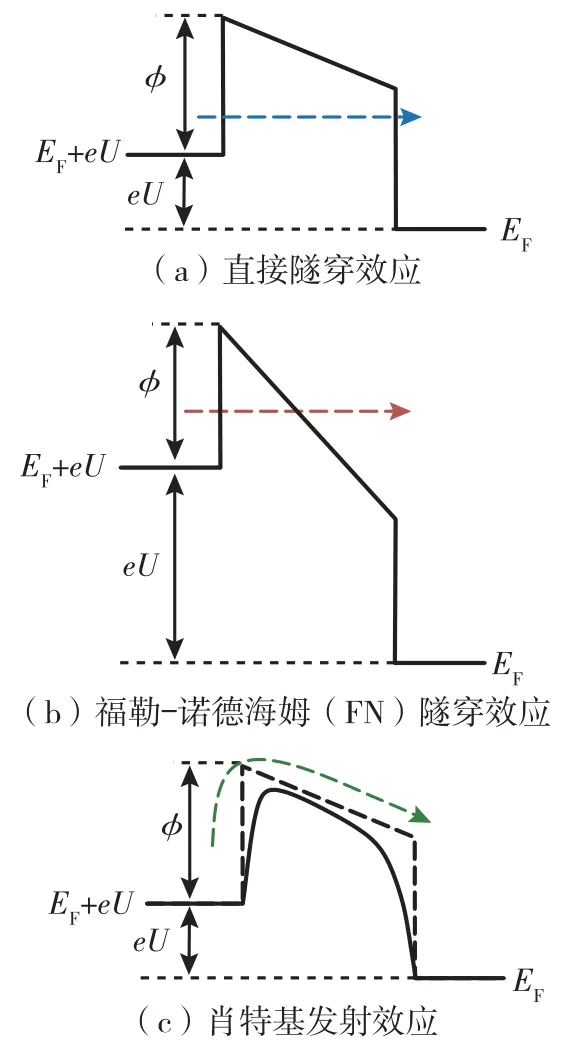
图2 三种主要电子输运效应的能级示意图Fig.2 Energy level schematic diagram of the three main electronic transport effects

2.2 直接隧穿效应与电流密度模型

分析直接隧穿效应是否为金属/空气/金属微观界面中产生电流的电子输运主要机理,需计算获取该效应的电流特性并与实际情况进行比较。当前针对电子直接隧穿的电流建模方法研究集中于STM 和半导体器件领域,前者的针尖模型可采用一维隧穿模型近似分析,且因其参与传感的原子规模较小,理论上针尖末端的原子贡献了绝大部分的电流[2],如采用转移哈密顿法、非平衡格林函数法等对其进行三维建模的计算量也在合理范围内;后者结构相对简单,容易获取有效隧穿面积,一般采用一维电流密度即可满足分析需要。然而,针对百微米甚至更大直径的球形敏感单元瞄准被测面的模型,目前尚无适宜的隧穿电流计算方法。因此,为分析直接隧穿特性并判断其是否为微观界面中电子输运产生的主要机理,采用电流密度模型对其特性进行分析。

金属/空气/金属微观界面的直接隧穿电流密度简化计算的能级示意如图3 所示,利用J.Simmons[3]提出如式(1)所示的电流密度公式可计算直接隧穿净电流密度。分析时采用零温度假设,将电极间电子传输限制为隧穿效应。由于电子隧穿效应对温度不敏感,零温度假设下计算得到的电流密度可表征常温下的规律。

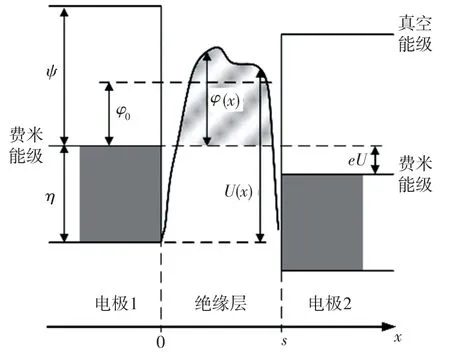
图3 直接隧穿电流密度的简化计算能级示意图Fig.3 Schematic diagram of energy levels for direct tunneling current density calculation

式中:J——隧穿电流密度,A/m2;m——电子质量,m=9.109 38 × 10-31kg;φ0——平均势垒高度,eV;s——绝缘薄层的厚度,m;e——电子电荷量,e=-1.602 18×10-19C;h——普朗克常量,h=6.626 07×10-34J·s;U——绝缘层两侧电势差即偏置电压,V;φ(x)——势垒高度随位置x变化的函数,eV。

确定偏置电压U与势垒高度φ0即可得到直接隧穿电流密度随间隙的变化规律。考虑到传感方法的实际应用情况,令偏置电压范围为0.01～10 V。金属/绝缘体界面的势垒高度为金属的功函数与绝缘层电子亲和势之差[4,5],真空中该值即等于金属的功函数。常见金属的功函数均在4.5 eV 左右[6],故分析时选择将4.5 eV 作为势垒高度的上限;此外,由于空气中存在气体分子,且金属表面可能存在氧化物薄层和其他杂质,势垒高度受到影响。有研究表明金属/空气界面的势垒高度可低至0.5 eV[7,8],因此分析时势垒高度范围取0.5～4.5 eV。在该条件下对直接隧穿产生的电流密度与间隙的关系进行分析。

通过分析直接隧穿电流密度与等效隧穿面积,预估直接隧穿机理效应电流的量值和规律。实际传感过程中0.1 nA 的电流信号已极其微弱,该量级的电流信号极易受到干扰,已接近常规可精确探测的下限。而如需通过直接隧穿产生0.1 nA 量级的电流,则在1 A/m2的电流密度下等效隧穿面积需达到1 ×10-10m2,该区域等价于直径为11.3 μm 的圆。对于直径为ϕ100 μm 至毫米量级的球形敏感单元,基于隧穿电流对间隙极为敏感的特性,可以判断该有效隧穿区域面积应为一较激进的估计。因此,当间隙变化对应的电流密度降低至1 A/m2时,可认为对应的直接隧穿电流已减小至几乎不可探测的量级。

1 V 偏置电压下,不同势垒高度的直接隧穿电流密度与间隙的关系如图4 所示。当势垒高度大于1 eV 时,10 nm 间隙对应的隧穿电流密度已降低至1×10-20A/m2量级;而即便势垒高度降低至0.5 eV,直接隧穿电流密度迅速减小至几乎不可探测量级的趋势并未改变。因此,1 V 偏置电压下直接隧穿效应产生电子输运的情况与实际不相符。

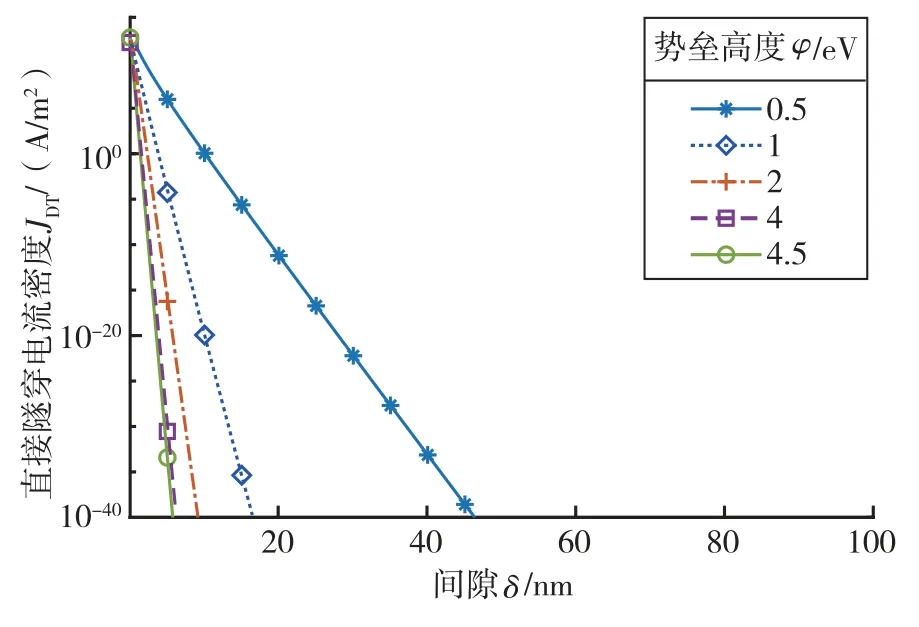
图4 1 V 偏置电压下不同势垒高度对应的直接隧穿电流密度与间隙的关系曲线图Fig.4 Relationship between direct tunneling current density and gap for different potential barriers at bias voltage of 1 V (linear-log scale)

为分析直接隧穿效应的极限情况,将势垒高度设为0.5 eV,此时不同偏置电压下的计算结果如图5 所示,可知当间隙大于50 nm 时直接隧穿电流密度已减小至几乎不可探测量级的规律并未改变。虽然偏置电压高于5 V 时可在大间隙下产生可探测的隧穿电流,但该条件下发生的隧穿现象应为福勒-诺德海姆隧穿。隧穿电流密度与间隙曲线出现了不单调甚至负值(图5 中未画出)的情况,其原因是当偏置电压较高且间隙较小时,直接隧穿公式不适于表征该情况,因而采用式(1)计算电流密度出现错误。综上可以确定,当间隙增加到10 nm 甚至更大时,直接隧穿电子输运机理产生的电流与实际情况不吻合。

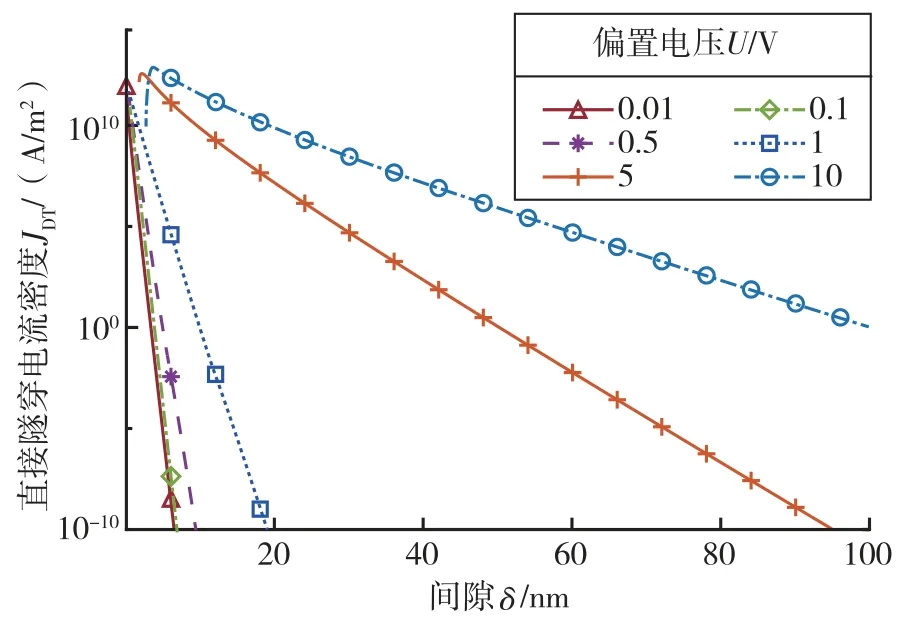
图5 0.5 eV 势垒高度下偏置电压取不同值时直接隧穿电流密度与间隙的关系曲线图Fig.5 Relationship between direct tunneling current density and gap for different values of bias voltage at potential barrier height of 0.5 eV (linear-log scale)

2.3 福勒-诺德海姆隧穿效应与电流密度模型

如图2 所示,当偏置电压U满足eU＞φ时发生福勒-诺德海姆隧穿效应。1928 年,Fowler R 和Nordheim L[1]提出了著名的福勒-诺德海姆隧穿公式来表征该物理过程,经修正的福勒-诺德海姆隧穿公式[9]如式(2)所示

式中:JFN——福勒-诺德海姆隧穿电流密度,A/m2;aFN——第一福勒-诺德海姆常数,aFN=e3/16π2h≈1.541 4×10-6,AeV-1;E——电场强度,V/m;φ——势垒高度,eV;bFN——第二福勒-诺德海姆常数,bFN=4(2m)1/2/3eh≈6.830 89×109,e-3/2V-1/2m-1。

其中,

式中:a——绝缘层厚度,m。

与直接隧穿效应相同,同样采用电流密度对福勒-诺德海姆隧穿效应进行分析判断。由于福勒-诺德海姆隧穿效应对温度不敏感,式(2)可近似表征室温下的福勒-诺德海姆隧穿电流密度[9]。且由于偏置电压较大,金属/空气/金属微观界面的福勒-诺德海姆隧穿电流计算可用单向电流近似净电流。根据式(2)计算福勒-诺德海姆隧穿电流密度随间隙的变化规律,计算时采取与直接隧穿分析时相似的条件。5 V 偏置电压下不同势垒高度对应的电流密度与间隙的关系如图6 所示,在势垒高度不小于1 eV 的情况下,20 nm 间隙对应的隧穿电流密度均已降低至1 A/m2量级。因此,间隙继续增大时,电流将迅速降低至几乎不可测的量级。

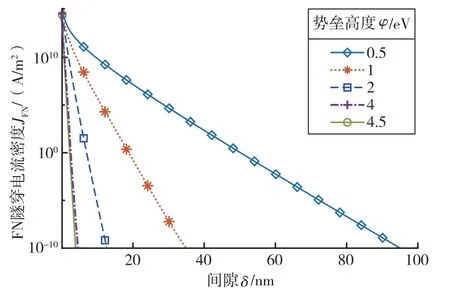
图6 5 V 偏置电压下不同势垒高度的福勒-诺德海姆隧穿电流密度与间隙的关系曲线图Fig.6 Relationship between FN tunneling current density and gap for different potential barriers at bias voltage of 5 V (linear-log scale)

势垒高度为0.5 eV 时,不同偏置电压下的计算结果如图7 所示。可知当偏置电压高至10 V 时,基于福勒-诺德海姆隧穿的电子输运机理有望在间隙增大至100 nm 时仍产生不低于0.1 nA 量级的隧穿电流。综上,当间隙增加到100 nm,在势垒高度接近0.5 eV,且偏置电压接近或达到10 V 的条件下,福勒-诺德海姆隧穿效应有可能是传感过程中电子输运产生的主要机理。

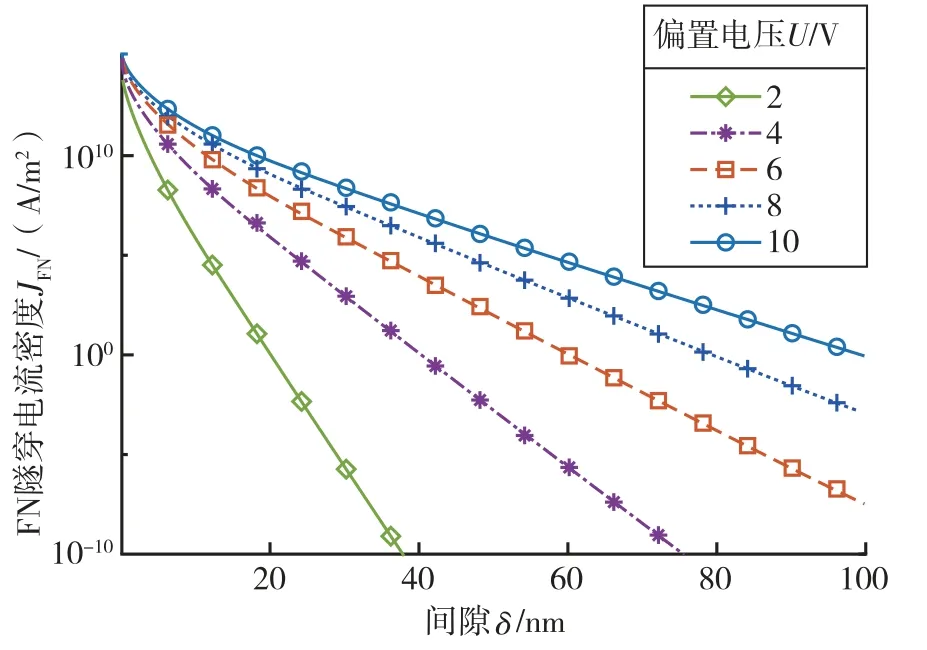
图7 0.5 eV 势垒高度下不同偏置电压的福勒-诺德海姆隧穿电流密度与间隙的关系曲线图Fig.7 Relationship between FN tunneling current density and gap for different values of bias voltage at potential barrier height of 0.5 eV

2.4 肖特基发射效应与电流密度模型

肖特基发射效应又称电场增强热电子发射效应(Field-enhanced Thermionic Emission)。如图2 所示,它与电子隧穿效应最大的区别是金属中的电子具备足够的能量可以直接跨越界面的势垒并到达另一侧电极。该效应发生的一个关键是偏置电场,其存在有效降低了势垒高度从而增大了发射电流。常温下金属/空气界面发生肖特基发射效应的可能性已被证实[10],并且有学者认为肖特基发射效应也是STM 在空气中产生传感电流的电子输运机理之一[11]。因此有必要对肖特基发射效应产生的电流进行分析,以确认非接触式传感过程中电子输运的主要机理是否为肖特基发射效应。

金属/真空界面产生的肖特基发射电流密度如式(4)所示的理查森-杜什曼方程(Richardson-Dushman Equation)给出[12]

式中:A——理查森常数(Richardson constant),A=4πmek2/h3,其值为1.201 7 ×106,A·m-2·K-2;k——波尔兹曼常数,eV·K-1;T——绝对温度,K。

金属微球/空气/金属被测面结构中产生的总电流为两个方向电流的叠加,在式(4)的基础上可得到金属/绝缘体/金属结构的净电流[12]如式(5)所示

式中:K——相对介电常数;s——绝缘层厚度,m;φ0——势垒高度,eV。

当s≫7/(UK)且eU＞2kT时,式(5)可以简化为[12]式(6)

据此计算不同偏置电压和不同势垒高度条件下肖特基发射电流密度与间隙的关系。计算时温度T设置为室温20 ℃即293.15 K,则此时偏置电压U应不小于0.05 V。而当偏置电压较小时,大间隙情况下电流密度的计算结果更准确。势垒高度取值范围与上文分析电子隧穿电流密度时相同。偏置电压为1 V 时的计算结果如图8 所示,除势垒高度为0.5 eV 的情况,10 nm 间隙对应的肖特基发射电流密度均已降低到1 A/m2量级。而当偏置电压为10 V 时,根据如图9 所示的计算结果,1 eV 势垒高度下,肖特基发射电子输运有望在间隙为100 nm时产生可探测的电流。而由图10 可知,当势垒高度降低至0.5 eV,且偏置电压大于0.1 V时,在百纳米间隙下仍可产生探测的电流。因此从传感电流幅值的角度分析,肖特基发射效应有可能是传感过程电子输运产生的机理。

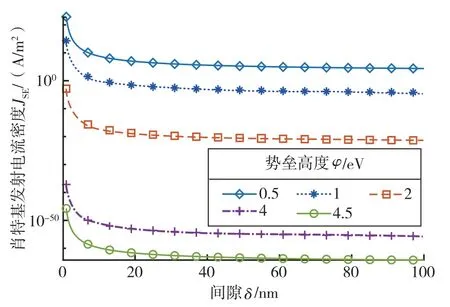
图8 1 V 偏置电压下不同势垒高度肖特基发射电流密度与间隙关系图Fig.8 Relationship between Schottky emission current density and gap for different potential barriers at bias voltage of 1 V

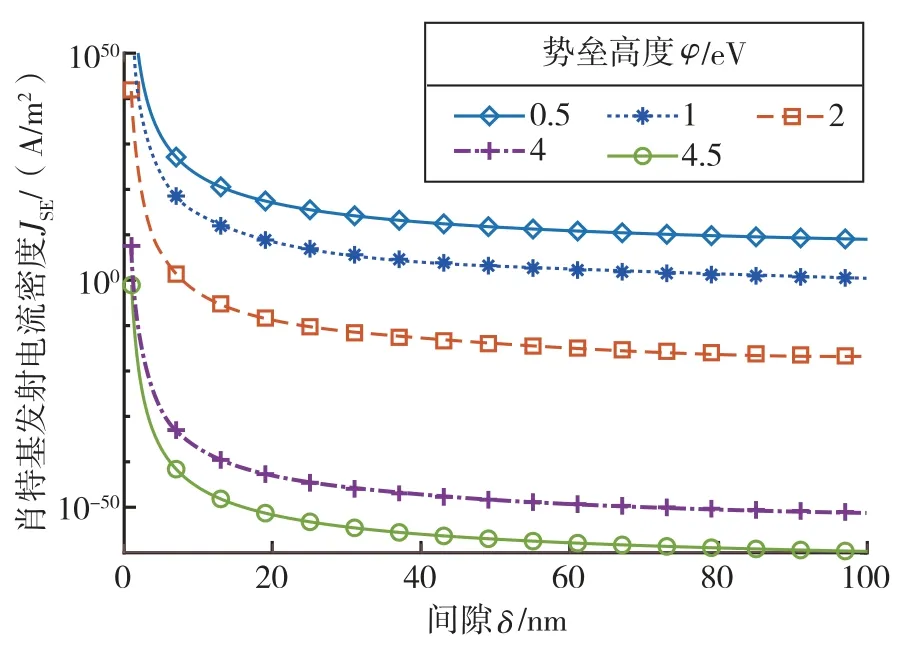
图9 10 V 偏置电压下不同势垒高度肖特基发射电流密度与间隙关系图Fig.9 Relationship between Schottky emission current density and gap for different potential barriers at bias voltage of 10 V

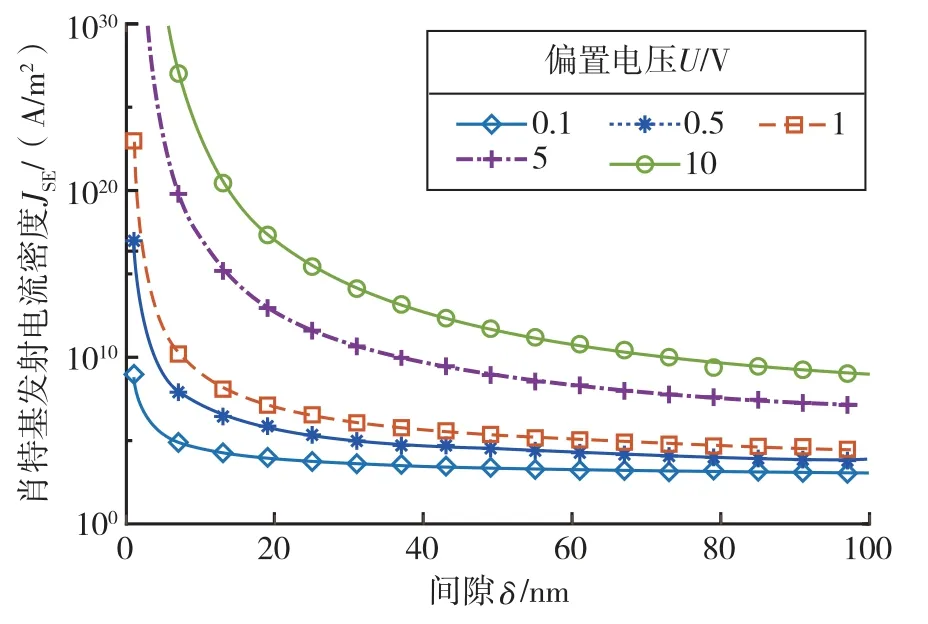
图10 0.5 eV 势垒高度下偏置电压取不同值肖特基发射电流密度与间隙关系图Fig.10 Relationship between Schottky emission current density and gap for different bias voltages at potential barrier of 0.5 eV

然而,从传感电流随间隙增大而减小的趋势角度分析,肖特基发射电流密度随间隙的增大而减小,在间隙大于50 nm 的情况下,电流衰减速率显著放缓。但实际测试中,当间隙调整至传感电流处于百纳安范围内时,随间隙增大传感电流衰减的速度保持一致或进一步加快,与肖特基发射规律相悖。因此,尽管在势垒高度较低的条件下电流幅值也可符合实际情况,从电流变化趋势角度分析肖特基发射电子输运产生电流与实际情况不吻合。

2.5 其他机理分析

基于欧姆定律分析可得知,空气薄层中因欧姆导电机理而产生的电流可忽略。此外,当金属/空气/金属微观界面性质发生改变,即空气构成的绝缘介质薄层被突破时,电子输运现象也会发生。界面中空气薄层发生性质改变有介电击穿效应和被局部突破而产生机械与电接触两种情况,分别分析其电子输运规律及对传感电流的影响,可知其在电子输运过程中所起作用均非常微弱。

综上,从传感电流的幅值角度分析,绝缘介质薄层电子输运机理中仅福勒-诺德海姆隧穿和肖特基发射有可能是金属/空气/金属微观界面中电流产生的电子输运主要机理,而这两种机理在100 nm的间隙下仍能产生可探测电流的前提条件均为较小(＜1 eV)的势垒高度。而结合传感电流随间隙增大而迅速减小的趋势判断,福勒-诺德海姆隧穿应为传感过程中电子输运产生的主要机理。

3 结束语

针对金属球形敏感单元瞄准金属被测面形成的金属/空气/金属微观界面,分析并阐明了该界面中电子输运产生的主要机理。由加载偏置电压时金属/空气/金属微观界面电子输运产生的机理分析可知,直接隧穿效应在间隙大于10 nm 的常规条件下产生的电流远小于nA 量级;福勒-诺德海姆隧穿效应与肖特基发射效应在势垒高度低于1 eV的情况下,均有可能在100 nm 间隙下产生nA 量级的电流,但后者电流密度随间隙增大而减小的变化速率与实际情况不符。而经理论分析与计算,其他机理在电子输运过程中所起作用非常微弱。由此,球形敏感单元微瞄准形成的金属/空气/金属微观界面中,产生传感电流的电子输运主要机理为福勒-诺德海姆隧穿效应得到揭示,该结论为探索新原理的三维非接触式纳米传感方法奠定了基础。