旋转对置活塞发动机运动学特性研究
2024-04-24王余枫高建兵赵玉伟黄俊峰宋纪龙付忠惠杨策
王余枫,高建兵,赵玉伟,黄俊峰,宋纪龙,付忠惠,杨策
(1.北京理工大学 机械与车辆学院,北京 100081;2.空军工程大学 防空反导学院,陕西,西安 710051)
内燃机的小型化、轻量化已成为未来的发展趋势[1].往复式活塞内燃机功率密度的大幅提升已成为制约其发展的瓶颈[2],因此不少学者致力于研究高功率密度新型内燃机[3-6].高建兵等[7]发明了一种旋转对置活塞(opposed rotary piston, ORP)发动机,该发动机具有结构紧凑、功率密度高、运行平稳等优点,符合混合动力汽车、小型无人机、装甲车辆辅助动力系统的需求,特别是对于小型无人机,由于这类发动机的功重比远远高于其他产品,可以实现长航时的技术要求[8].陈虎[9]设计了一种双转子活塞发动机,分析了其做功原理,发明了一种基于摆盘和凸轮组合机构的动力输出装置,分析了结构参数如滚子轴线夹角和摆盘倾角,对其容积变化规律的影响,但其结构较为复杂,燃烧室狭长且对滚子轴线夹角精度要求较高.高建兵等[10]率先将氢燃料应用于结构简单的ORP 发动机,探索了燃氢条件下回火的有效控制策略.此外,针对ORP 发动机的换气特性、缸内燃烧及排放特性等也开展了大量的研究[11-13].
对于传统的往复式活塞发动机,其活塞运动规律由曲柄连杆机构进行约束,而ORP 发动机的活塞运动规律由动力输出装置进行约束.ORP 发动机的动力输出装置由两对相互啮合的二阶椭圆齿轮组成[14],实现了相邻活塞的同向差速运动.周凯红等[15]探究了高阶椭圆齿轮传动规律,表明二阶椭圆齿轮副的角速度呈周期性变化;当偏心率增加时,速度波动逐渐增大.二阶椭圆齿轮的瞬时传动比随时间不断变化,因此造成活塞速度的周期性变化,符合ORP发动机对活塞运动模式的需求,且椭圆齿轮可以较好地缓解传统曲柄连杆机构和配气机构带来的平衡和噪音问题[16].
GAO 等[17]通过电动机反拖ORP 发动机获得理想的活塞运动规律,并且对采集到的离散点进行拟合,获得活塞的角速度曲线,但并未针对活塞运动的约束条件以及ORP 发动机的结构参数对活塞运动规律的影响开展研究.为了确保ORP 发动机缸内新鲜混合气的高效燃烧及动力的稳定输出,活塞运动规律控制以及相关影响因素的探究是亟待解决的关键问题.文中研究了ORP 发动机结构参数对活塞运动规律的影响;探讨了结构参数对活塞线速度、气缸容积变化规律、压缩比变化等的影响,为ORP 发动机的优化设计提供理论指导.
1 ORP 发动机结构参数
ORP 发动机主要由做功系统和动力输出装置组成,其结构简图如图1 所示.做功系统由发动机缸体、两对活塞、粗轴和动力输出轴组成,并且两轴同心[14];动力输出装置由两对相互啮合的二阶椭圆齿轮及支撑轴组成.相邻活塞角速度的周期性变化导致气缸容积的周期性变化,动力输出轴转过一周,每个气缸可完成一次吸气—压缩—膨胀—排气的工作过程,因此做功频率为往复活塞式发动机的两倍[17],其做功过程原理在文献[6, 10]中有详细介绍.
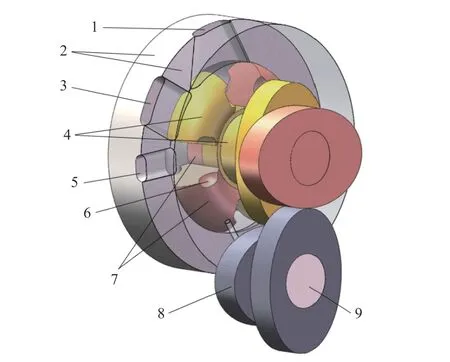
图1 ORP 发动机结构简图Fig.1 Schematic diagram of the ORP engine structure
1.1 气缸结构参数
ORP 发动机做功系统的主要结构如图2 所示.活塞的截面为扇形,θ为活塞端面夹角.图3 中展示了气缸的主要结构参数:扇形的半径为R0,半弦长为L,弦与活塞截面圆心的距离为,R为活塞弦面距轴中心线的距离.
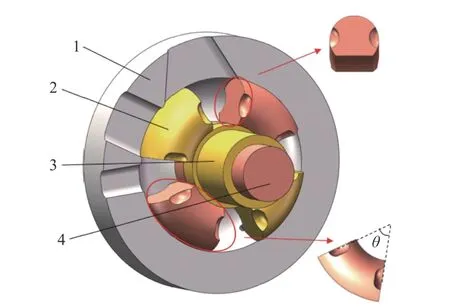
图2 做功系统结构Fig.2 Structural configuration of the power generation system

图3 气缸截面参数Fig.3 Parameters of cylinder cross-section
1.2 动力输出装置结构参数
ORP 发动机动力输出装置采用两组二阶共轭椭圆齿轮副组成,4 个椭圆齿轮节曲线完全相同,如图4 所示.动力输出轴6 与齿轮1 刚性连接,粗轴7与齿轮4 刚性连接.齿轮2 和3 均与支撑轴5 刚性连接,并且限制了齿轮1 和齿轮4 的相对运动,进而实现活塞特定的运动规律,实现了气缸容积的规律性变化.李飞等[18]提供了二阶椭圆节曲线方程,其方程与长半轴a及偏心率e有关,具体分析见下文.
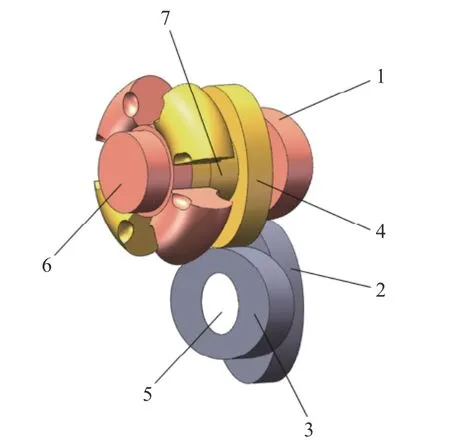
图4 动力输出装置结构简图Fig.4 Schematic diagram of power output device structure
2 ORP 发动机动力传递计算方法
由1.2 节及图4 可知,齿轮1 与动力输出轴及相应活塞刚性连接,动力输出轴匀速运动.由于共轭椭圆齿轮副的约束,与粗轴刚性连接的活塞只能以特定的规律运动.二阶椭圆齿轮的轴心位于节曲线几何中心[19],其特有的传动特性使活塞转动一周即完成吸气—压缩—膨胀—排气冲程,动力传递计算过程中将发动机工作过程视为理想状态,不考虑机械传动损失、壁面摩擦等因素引起受力改变的情况[20].
2.1 椭圆齿轮传动分析
二阶椭圆齿轮的节曲线极坐标方程为[18]
式中:r(φ)为法向距离,m;φ为节曲线法线与x轴夹角,rad;a为椭圆节曲线长半轴,m;e为椭圆节曲线的偏心率.
按照图4,定义动力输出轴匀速转动的角速度为ω1(rad/s),根据二阶椭圆齿轮传动比函数为[15]
式中:i12为椭圆齿轮1、2 的传动比;ω2为椭圆齿轮2的角速度,rad/s;r1为齿轮1 节曲线的径向距离,m;r2为齿轮2 节曲线的径向距离,m.
齿轮2 的角速度ω2为
式中t为时间,s.
由于齿轮2、3 无相对运动,因此齿轮3 的角速度ω3为
齿轮4 的角速度ω4为
2.2 活塞运动规律分析
由于两组对置的活塞分别与粗轴和动力输出轴刚性连接,因此,ω1与ω4为相应活塞运动的角速度,两对活塞转过的角度θ1(t)、θ2(t)及两个相邻活塞间的角度差Δθ(t)见式(6)、(7)和(8).
两组活塞几何中心的线速度v1和v2分别为
气缸剖面与活塞剖面形状一致,由扇形旋转而成的整个环形区域的体积Vtot为
为了增强气缸内组分的湍流强度以及扩大点火范围,提出了ORP 发动机活塞端面设计凹坑[6](见图2).单个凹坑体积为V0,则气缸瞬时容积为
则相邻气缸容积同理也可求得.
压缩比为活塞运动过程中,气缸最大容积与最小容积之比为[17]
3 结果与分析
本节以已出版的文献[6, 17]中ORP 发动机的结构尺寸为基准值,见表1,采用控制变量法,通过对每个参数进行±10%、±5%变动,探究不同参数变化对ORP 发动机活塞的运动线速度、气缸容积、压缩比的影响规律.

表1 ORP 发动机参数Tab.1 Parameters of ORP engine
3.1 活塞运动规律
由式(9)、(10)可知,与活塞运动线速度相关的结构参数包含R0、L、R、e.与动力输出轴相连的活塞速度不随时间变化,因此本小节仅讨论变速活塞的线速度变化.针对活塞线速度,按照表1 中基准参数分析了活塞线速度对参数R0、L、R、e变化的敏感性,结果如图5 所示.活塞速度变化规律与文献[17]有较好的一致性.
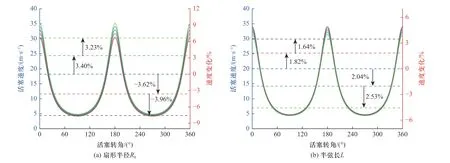
图5 活塞线速度变化规律Fig.5 Variation law of piston linear velocity
由图5 可知,R0、L、R的变化导致活塞线速度在整个周期内均匀变化.从图5(a)和图5(c)可得,随着R0、R的增大,活塞线速度均有所增大;线速度增长趋势随着R0的增加而减小;当R0在-10%~5%以及5%~10%之间变化时,活塞线速度分别增长了3.96%和 3.23%.线速度变化与R呈正比例趋势,R每增加5%,活塞线速度增长3.47%.从图5(b)可得,与R0、R的敏感性不同,活塞线速度随着L的增大而减小,L在-10%~5%以及5%~10%之间变化时,线速度分别减小了1.64%和2.53%,线速度减小趋势随着L的增大而增大.由图5(d)可知,不同于R0、L、R,偏心率e的变化会带来线速度在整个周期内的非均匀变化,这是因为e的变化导致椭圆齿轮4 的角速度ω4在整个运动周期内均发生变化.在整个运动周期内,在线速度最小时刻,活塞线速度随着e的增加而减小,下降率随着e的增加而减小;而在线速度最大时刻,活塞线速度随着e的增大而增大,且增长率随着e的增大而增大.
在参数R0、L、R变动时,活塞线速度在运动周期内各时刻均呈现等比例增大或减小.e变化时,活塞线速度呈现非等比变化:当线速度小于平均值时,线速度随e的增大而减小;当线速度大于平均值时,线速度随e的增大而增大.因此,随着e的增大,活塞的速度波动越来越大,若速度波动导致形变则会引起活塞组件与缸套配合间隙的变化,进而影响燃烧室的密封与活塞缸套间的摩擦传热[21],在后续ORP 发动机结构优化时,e值的选择需要考虑速度波动造成的受力变化等问题.
3.2 气缸容积变化规律
由图2 气缸结构可知,相邻的两个气缸容积之和在发动机运行过程中始终保持不变,因此,本小节仅讨论其中一个气缸容积的变化规律,可间接反映与其相邻的气缸的变化规律.由式(12)可知,其容积变化与参数R0、L、R、e、θ、V0有关,因此,本节分析了气缸容积变化规律随以上参数的变化情况,计算结果见图6.
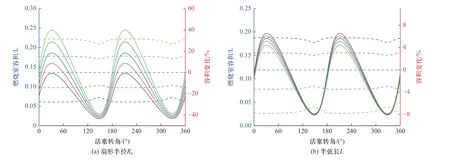
图6 气缸容积变化规律Fig.6 Variation law of cylinder volume
由图6(a)可见,随着R0的增大,气缸容积在整个运动周期内均增大,并且变化率增加趋势也增大,在气缸容积最大时,即下止点,气缸容积对R0的变化最为敏感;在气缸容积最小时,即上止点,容积对R0变化的敏感度最小,这是因为活塞凹坑的体积不随活塞转角的变化而变化,属于气缸的固有体积.由图6(b)可见,气缸容积随着L的增大而减小,减小趋势也随之增加,与R0相似,在上止点时,由于活塞凹坑的存在,敏感度略有减小.图6(c)所示为参数R变化对气缸容积的影响,在整个运动周期内,R增大导致气缸容积增大,与R0不同的是,气缸容积对R变化的敏感度相对较小,且容积变化趋势呈均匀分布.由图6(d)可知,e变化会导致气缸容积在整个运动周期内的不均匀变化,在活塞下止点前后,气缸容积随着e的增大而增大,在活塞上止点附近则变化相反,在下止点时,容积对e的变化最为敏感.
图6(e)为活塞两端面夹角对气缸容积的影响,θ增大,气缸容积在整个运动周期内均减小,且敏感性随时间变化,在上止点时最为敏感,并且当θ减小10%、气缸容积可减小70%.由图6(f)可见,气缸容积随着V0的增大而增大,且对V0的敏感性较小,在活塞上止点附近波动有所增大,当V0增大10%时,上止点时刻气缸容积增大1.5%.
通过调整R0、L、R、e、θ、V0均可改变运动过程中的气缸容积,其中调整R0、L、R的值可使得气缸容积在整个运动周期内呈现近似均匀的增大或减小,气缸容积与R0、R的值呈正相关变化趋势,与L的值呈负相关变化趋势.调整e、θ、V0可使气缸容积在整个运动周期内非均匀变化,其中调整e可使气缸容积在上止点与下止点按相反的趋势变动,因此可改变ORP 发动机压缩比;调整θ可使气缸容积在运动周期内均增大或减小,当活塞运动到上止点时,容积对θ的变化最为敏感;参数V0的变化对气缸容积影响较小,仅在上止点附近敏感度有所增强.
3.3 压缩比变化规律
ORP 发动机压缩比定义为活塞旋转运动形成的最大气缸容积与最小气缸容积之比[17].由式(13)可知,压缩比与相邻活塞间的角度、整个环形气缸的体积及凹坑体积V0有关.基于3.2 节气缸容积数据,在各参数变动时,计算出每种设定参数下气缸最大容积与最小容积之比即为压缩比,其变化情况如图7所示.

图7 压缩比变化规律Fig.7 Variation law of compression ratio
由图7 可知,压缩比的变化与R0、R、e、θ呈正相关变化趋势,与L与V0呈负相关变化趋势.e与θ对压缩比的影响最大,随着e的增大,压缩比的增长率也增大;相较于压缩比基准值的7.80,在±10%的范围内调整e的值可使压缩比在5.62~12.04 的范围内变动,变化区间为-27.94%~54.42%,在同样的范围内调整θ的值即可使压缩比在5.01~23.45 的范围内变动,变化区间为-35.81%~200.63%.提高e和θ的值可有效增大ORP 发动机的压缩比,能满足汽油、柴油、氨等燃料对压缩比的需求.
3.4 活塞碰撞条件
ORP 发动机活塞的运动由动力输出装置约束.当相邻活塞夹角过小时,活塞可能发生碰撞.由图2可知,当相邻活塞中心线夹角Δθ小于活塞两端面夹角θ时,相邻活塞即发生碰撞.参考式(8),相邻活塞不发生碰撞的条件为
即:
由上式可知,当活塞两端面夹角θ确定时,相邻活塞碰撞条件仅与二阶椭圆齿轮节曲线的偏心率e有关.参考表1 中方案,e在-10%~40%变化,气缸两端面夹角如图8 所示.由图可知,当e逐渐增大,相邻活塞形成的气缸两端面最小夹角小于0 度时,此时相邻活塞发生碰撞.为了避免相邻活塞发生碰撞,需减小椭圆齿轮e值或减小两活塞端面夹角θ.
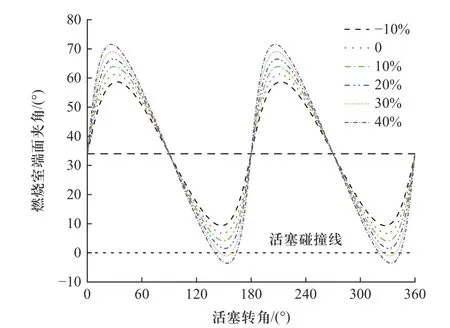
图8 气缸端面夹角Fig.8 Cylinder end face angle
4 结 论
文中基于ORP 发动机的结构参数构建了ORP发动机活塞运动线速度、气缸容积、压缩比及动力输出装置动力传递的数学模型,分析了活塞的运动规律及各参数对活塞运动线速度、气缸容积变化规律、压缩比的影响,为ORP 发动机的结构优化设计及可靠性分析奠定了理论基础.文中主要结论如下.
①参数R0、L、R的变化使活塞瞬时线速度在整个周期等比例变化,线速度变化与参数R0、R的值的变化呈正相关,与L值的变化呈负相关;e值的变化使得活塞线速度在运动周期内非等比变化,e增大使活塞运动线速度的波动变得更剧烈;活塞线速度对e的变化最为敏感,其次为R0和R,L次之.
②调整R0、L、R的值使气缸容积在整个运动周期内呈现较为均匀的变化,气缸容积与R0、R的值呈正相关变化趋势,与L的值呈负相关变化趋势;调整e、θ、V0的值使气缸容积在整个运动周期内非均匀变化,气缸容积最大值与最小值随e的变化趋势相反.θ对余隙容积影响最大,V0对气缸容积变化影响最小.
③压缩比与R0、R、e、θ的变化呈正相关,与L、V0的值呈负相关.压缩比对e、θ的变化最为敏感.相较于基准值,参数e在±10%的范围内调整时,压缩比的变化范围为5.62~12.04;参数θ在±10%的范围内调整时,压缩比的变化范围为5.01~23.45.
④椭圆齿轮偏心率e过大将导致活塞线速度波动增强甚至相邻活塞发生碰撞,减小e值或活塞端面夹角可避免活塞发生碰撞.
