Three-dimensional (3D) parametric measurements of individual gravels in the Gobi region using point cloud technique

JING Xiangyu, HUANG Weiyi, KAN Jiangming*

1 College of Engineering, Beijing Forestry University, Beijing 100083, China;

2 Key Laboratory of State Forestry Administration on Forestry Equipment and Automation, Beijing 100083, China

Abstract: Gobi spans a large area of China, surpassing the combined expanse of mobile dunes and semi-fixed dunes.Its presence significantly influences the movement of sand and dust.However, the complex origins and diverse materials constituting the Gobi result in notable differences in saltation processes across various Gobi surfaces.It is challenging to describe these processes according to a uniform morphology.Therefore, it becomes imperative to articulate surface characteristics through parameters such as the three-dimensional (3D) size and shape of gravel.Collecting morphology information for Gobi gravels is essential for studying its genesis and sand saltation.To enhance the efficiency and information yield of gravel parameter measurements, this study conducted field experiments in the Gobi region across Dunhuang City, Guazhou County, and Yumen City (administrated by Jiuquan City), Gansu Province, China in March 2023.A research framework and methodology for measuring 3D parameters of gravel using point cloud were developed, alongside improved calculation formulas for 3D parameters including gravel grain size, volume, flatness, roundness, sphericity, and equivalent grain size.Leveraging multi-view geometry technology for 3D reconstruction allowed for establishing an optimal data acquisition scheme characterized by high point cloud reconstruction efficiency and clear quality.Additionally, the proposed methodology incorporated point cloud clustering,segmentation, and filtering techniques to isolate individual gravel point clouds.Advanced point cloud algorithms, including the Oriented Bounding Box (OBB), point cloud slicing method, and point cloud triangulation, were then deployed to calculate the 3D parameters of individual gravels.These systematic processes allow precise and detailed characterization of individual gravels.For gravel grain size and volume, the correlation coefficients between point cloud and manual measurements all exceeded 0.9000,confirming the feasibility of the proposed methodology for measuring 3D parameters of individual gravels.The proposed workflow yields accurate calculations of relevant parameters for Gobi gravels,providing essential data support for subsequent studies on Gobi environments.

Keywords: Gobi gravels; three-dimensional (3D) parameters; point cloud; 3D reconstruction; Random Sample Consensus (RANSAC) algorithm; Density-Based Spatial Clustering of Applications with Noise (DBSCAN)

1 Introduction

Gobi is a quintessential surface landscape type in the arid regions of northwestern China, which has been shaped by prolonged wind erosion and physical weathering into a desert, predominantly consisting of gravels and rubbles (Feng et al., 2013).Its presence is widespread across vast expanses of open land, particularly in regions like Xinjiang Uygur Autonomous Region (Cheng et al., 2015), Inner Mongolia Autonomous Region (Gao et al., 2020), Qinghai Province (Zhang,2019), and Gansu Province (Ta et al., 2003), as well as areas such as Junggar Basin, Qaidam Basin, Tarim Basin, Alxa Plateau, and Hexi Corridor (Feng et al., 2014; Dong and Lyu, 2020) in China.The Gobi gravel surface plays a crucial role in the ecological landscape, with highly representative and unique formation and evolutionary processes (Li et al., 2014).Analyzing the composition, morphological structure, distribution pattern, anisotropy, and other parameters of gravels on the Gobi's surface not only reveals lithological characteristics of the area but also provides evidence of the environmental conditions and historical development of the Gobi(Bockheim, 2010; Gao, 2019).Moreover, investigating the morphological characteristics of Gobi gravels is an important prerequisite for research in this area (Liang et al., 2023), facilitating a workable understanding of local ecosystem functions, wind and sand activity patterns, and necessary steps toward the sustainable development of Gobi resources and environmental management in future endeavors.

Gravels, defined as mineral particles with grain sizes ranging from 2 mm to less than 76 mm(Yao, 2014), have not yet been extensively researched in the Gobi region due to its harsh natural conditions and sparse population.Conducting field studies in this remote and inhospitable area is challenging.Traditional methods for measuring gravel characteristics involve human-dependent empirical visual observations (Claude et al., 2012), field measurements (Liu et al., 2022), and image-based methods (Jia, 2022).Visual observations are susceptible to the subjective judgment of the researchers, leading to relatively low accuracy (Tao et al., 2015).Field measurements,encompassing techniques like the sieve method, scale measurement, enumeration method, and adhesive method (Diplas and Sutherland, 1988; Bunte and Abt, 2001; Mu, 2017), are commonly utilized but can be excessively labor-intensive.Recent advancements in image processing technology have led to indirect analysis techniques for gravel surface characteristic parameters(Matthew, 2010; Wang, 2013; Babaeian et al., 2019; Yaghoobi et al., 2019; Shrivastava et al.,2022).Image-based methods offer advantages such as non-contact measurement, repeatability,and high accuracy.They can generally be categorized into three groups: manual marker measurement method, semi-automatic image analysis method, and fully automatic image analysis method.Additionally, some researchers have utilized remote sensing images to analyze gravel surfaces (Zhao, 2021).However, a fundamental challenge in employing remote sensing images for grain size inversion of granular materials lies in establishing a quantitative relationship between grain size and remote sensing data.

Many previous studies have employed image-based methods to quantify the morphological parameters of gravels, with some qualitatively comparing different measurement approaches.For instance, Wang (2005) devised a system relying on binary digital images to analyze gravel grain size.Qian et al.(2014) measured and analyzed parameters such as gravel coverage and gravel grain size in photographs of the Gobi surface taken from the ground using a photographic method with ImageJ software.Their method exhibits high accuracy, but requires substantial time for gravel vectorization.Furthermore, image-based measurement techniques can only typically capture two-dimensional (2D) information for gravel particles, failing to fully represent the three-dimensional (3D) morphological characteristics of gravel surface.

Advancements in 3D technology have allowed for extensive geometric, shape, and scale data to be gathered for use in various fields including geological research (Arnold et al., 2019).Indeed,digital models and 3D techniques have become increasingly prevalent in geological research(Westoby et al., 2012).Al-Rawabdeh et al.(2016) employed unmanned aerial vehicle (UAV) tilt photogrammetry to generate 3D point cloud data and automatically detect fault walls at the rear edge of landslides.Obanawa and Hayakawa (2018) combined drone photography with ground-based laser scanning equipment to conduct topographic surveys of cliffs in eastern Japan,and investigate the impact of waves on sea cliff erosion.Agüera-Vega et al.(2020) analyzed the influence of point cloud density, spatial resolution, and interpolation methods on the generation of surface elevation information over small scales.Many other scholars have applied 3D technology to gravel-related research, including Computed Tomography (CT) scanning, Light Detection and Ranging (LiDAR) scanning, and 3D reconstruction based on multi-view images (Fouinat et al.,2017; Zamani et al., 2019; Tonina et al., 2020).Applying these techniques in the field revealed a strong correlation between particle roughness and size (Vázquez-Tarrío et al., 2017).

Additionally, some scholars have reconstructed drone-based images to extract information on the size, circularity, and orientation of rocks, enhancing analyses of rock characteristics on fault cliffs (Chen et al., 2020).Importantly, this technology is not limited to real-world scenarios but is also applicable in laboratory experiments.For example, Ojeda-Magaña et al.(2020) determined the geometry and spatial distribution of elements in soil samples through CT scanning.They successfully separated sand grains from gravels within the soil and accurately calculated their individual representations and spatial distributions in the samples.However, damage to the soil during sampling is irreversible, and the experiment lacks reproducibility.

Hossein Rahmani et al.(2019) utilized an image-based technique to measure the size distribution of gravel particles within gravel-soil mixtures.They employed a LiDAR scanner and a surface reconstruction algorithm to produce high-resolution depth images, enabling the calculation of volume and weight for each gravel particle.Images were integrated with 3D point cloud techniques to comprehensively depict the obtained gravel parameters.However, the 3D scanner was placed on the top of the gravel particles, thus overlooking information at the bottom of the gravel particles.

Both surface parameters (e.g., roughness and surface elevation information) and individual gravel parameters (e.g., size, weight, and roundness) are important for the study of the subsurface that influences the pattern of wind-sand saltation in the Gobi region.However, the current focus of 3D point cloud research on gravels is predominantly centered around riverbeds (Bertin and Friedrich, 2016; Woodget and Austrums, 2017).Utilizing 3D point cloud for collecting and analyzing information on Gobi gravels has the potential to yield more comprehensive and accurate 3D information about these materials.The present study proposes acquiring point cloud data through close-range shooting based on computer vision technology, followed by measuring the 3D morphological parameters of gravels.Starting with the practical necessity for automated gravel morphology measurement, we first reconstructed a gravel point cloud model using multi-view geometry technology.The point cloud was then segmented to extract individual gravel point clouds, enabling calculation and measurement of 3D morphological parameters of individual gravels.This approach provides a reliable data source for further research and analysis of wind-sand movement in the Gobi region.

In summary, existing research on Gobi gravels primarily relies on traditional methods like visual observations, field measurements, and image-based methods, which are problematic in terms of subjectivity and limited accuracy.This study utilized an innovative approach for gravel parameter measurements in the Gobi region using point cloud technology, coupled with an improved calculation method for various gravel shapes.By addressing current research gaps, this study holds significant theoretical and practical implications.The results of this work may provide more reliable data support for understanding of aeolian sand movement in the Gobi region, thereby facilitating more effective management and conservation of its ecological environment.

2 Materials and methods

2.1 Gravel sampling and experimental design

Field experiments were conducted in the Gobi region, covering areas within Dunhuang City,Guazhou County, and Yumen City (administrated by Jiuquan City), Gansu Province, China.Jiuquan City spans approximately 680 km from east to west and 550 km from north to south.The overall elevation distribution in Jiuquan City exhibits a high north-south contrast and a low middle pattern (Zhang, 2022).The surface features of Jiuquan City are highly complex, encompassing the glaciated Qilian Mountains, vast alluvial plains, and a large and extended Gobi landscape.

According to previous study on the division of Gobi natural areas (Shen et al., 2016), the desert in Dunhuang City belongs to the Gobi subregion within the range of "Dunhuang-Kumtag residuum-cumulus and gravel".The main distribution in this area is the denudation-eluvial-type coarse Gobi gravels.To further refine the characterization, the area has been stratified based on variations in gravel coverage and grain size.These gradations are categorized into high, medium,and low coverage grades, as well as large, medium, and small particle-size grades.Representative gravel particles were sampled in this study from diverse sampling sites to ensure that the samples differed significantly in characteristics like shape and roundness.A total of 34 gravel samples were randomly selected from various sampling sites in the Gobi region.

Prior to commencing fieldwork, the research team prepared a variety of sampling tools,including standard vernier calipers for precise gravel grain size measurements, markers for labeling samples, and sealed bags to ensure that samples were not contaminated by the external environment after collection.During the field sampling process, we adopted a strict random sampling method.Samples were collected from random locations surrounding the sampling sites to ensure the representation of the geological diversity of the entire study area.This approach minimized subjective bias in sample collection and enhanced representativeness and reliability.Vernier calipers were used for detailed measurements of the randomly selected gravel samples,and triaxial grain size parameters were recorded for subsequent analysis.Each gravel sample was assigned a unique number and labeled accordingly to facilitate future traceability and investigation of its source and characteristics.

The calculation of 3D morphological parameters for individual gravels involved four main steps:point cloud data acquisition, segmentation, measurement, and calculation.The acquisition of gravel point cloud data encompassed image acquisition and 3D reconstruction (sparse reconstruction and dense reconstruction).Point cloud segmentation involved preprocessing,extraction of off-site gravel point clouds, and segmentation to extract individual gravels.The measurements of 3D parameters for gravels included triaxial grain size measurement, volume measurement, and other computations (e.g., roundness, flatness, sphericity, and equivalent grain size).

2.2 Gravel point cloud data acquisition

Point cloud data can be obtained through two primary methods: direct acquisition using 3D laser scanning equipment, or recovering 3D scene spatial information by collecting 2D images.Given that the latter method yields more original information, we selected it in this study to obtain point cloud data.The monocular vision-based image 3D reconstruction technique was first operated by acquiring multi-view 2D images, then extracting and matching image feature points, conducting point cloud sparse reconstruction based on Structure-from-Motion (SfM), and performing point cloud dense reconstruction based on Multi-View Stereo (MVS).COLMAP was chosen as the route for gravel point cloud acquisition.COLMAP is an implementation of integrated SfM and MVS method proposed by Schonberger and Frahm (2016), which offers both a command line and a graphical interface.The data acquisition process only necessitates continuous variation in the angle and relative position of the camera concerning the target while capturing images,eliminating the need for a priori camera calibration.

The gravel samples selected for parameter measurements were positioned against a wooden board background.The SONY DSC-RX100M5 model digital camera (Sony, Tokyo, Japan) with one-inch (13.2 mm×8.8 mm) Exmor RS CMOS image sensor (Sony, Tokyo, Japan) was utilized.During the shoot, we adjusted the focal length to approximately 12.8 mm, with an equivalent focal length of about 35.0 mm.When the camera's equivalent focal length is 35.0 mm, its angle of view is about 64°.For ease of calculation, the field of view angle was approximated to be 60°.The shots were centered on the gravel target, positioned approximately 50.0 cm away.Photographs were taken uniformly around the target from high, middle, and low angles of approximately 30°, 45°, and 60° from the horizontal surface, respectively.Given the field of view angle of approximately 60°, a full circle of photos required six images to cover the entire area.With each added circle of images, the overlap between consecutive images increased, leading to variations in the reconstructed point clouds.To explore these effects, we conducted the experiments with different degrees of overlap by recording the number of images collected, the number of dense point clouds, and the generation time for both sparse and dense point clouds(Table 1).The impact of varying degrees of overlap is depicted in Figure 1.It is evident that when the image overlap ratio was 1/3 or 1/2, there exhibited significant gaps at the bottom and sides;whereas the point clouds with image overlap ratios of 2/3, 3/4, and 4/5 were relatively complete.

Table 1 Comparison of three-dimensional (3D) reconstruction results with different degrees of image overlap

Fig.1 Comparison between different three-dimensional (3D) reconstruction results with image overlap ratios of 1/3 (a), 1/2 (b), 2/3 (c), 3/4 (d), and 4/5 (e)

The number of input images selected significantly impacts the quality of 3D reconstruction in point clouds.Insufficient input images can lead to a substantial reduction in matching feature point pairs, potentially causing inaccuracies in camera pose estimation.This, in turn, can result in significant omissions or mismatches during the dense point cloud generation process.Reconstruction accuracy improves as the number of input images increases, however, the time required for image matching also escalates, leading to reduced processing efficiency and increased redundancy.Hence, selecting an appropriate sampling spacing and acquiring the most effective quantity of image inputs is a crucial step to ensure both efficient and high-quality reconstruction of point clouds.In this study, a sampling interval of 2/3 overlap ratio between adjacent images was chosen, allowing for the reconstruction of gravel point clouds relatively quickly without sacrificing quality.Figure 2 provides a schematic diagram of gravel point cloud acquisition through 3D reconstruction using COLMAP.

Fig.2 Flowchart of gravel point cloud data acquisition (a) and pictures showing the sampling site environment(b), collected gravels (c), sparse reconstruction result based on Structure-from-Motion (SfM) (d), dense reconstruction result based on Multi-View Stereo (MVS) (e), and output point cloud data (f)

In acquiring gravel point cloud data, external factors related to camera pixels, shooting angle, and ambient light may generate a certain number of noisy or outlying points.To ensure a high degree of similarity between the point cloud model and real gravel particles, the following considerations were taken during gravel image data acquisition: (1) ensuring accurate focus of the digital camera;(2) controlling the shutter speed to prevent blurring; and (3) ensuring as close an overlap as possible between neighboring images while avoiding multiple acquisitions in the same area, and creating a uniformly distributed point cloud.

For data near the surface and at the bottom of the ground surface, the angle was adjusted as necessary to collect as much information as possible.For the data near the bottom of the ground surface, it was necessary to further adjust the angle to collect sufficient information.

2.3 Gravel point cloud clustering segmentation

Once the complete down-sampling gravel point cloud was obtained, it was segmented and clustered in its entirety to extract individual gravel point clouds for the measurement and calculation of 3D feature attributes of each individual gravel.Segmentation involved initially separating the foreground and background of the complete down-sampling gravel point cloud, and the Random Sample Consensus (RANSAC) algorithm (Fischler and Bolles, 1981) was applied to fit the surface plane and extract the off-site gravel point clouds constituting the complete down-sampling gravel point cloud.Subsequently, the off-site gravel point clouds were extracted using Density-Based Spatial Clustering of Applications with Noise (DBSCAN), and the off-site gravel point clouds in the foreground were divided into individual gravel point clouds.The complete gravel point cloud segmentation process is illustrated in Figure 3.

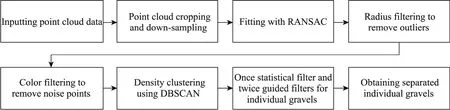
Fig.3 Flowchart of gravel point cloud segmentation.RANSAC, Random Sample Consensus; DBSCAN,Density-Based Spatial Clustering of Applications with Noise.

The RANSAC algorithm was primarily used to estimate the geometric parameters of a mathematical model from a set of measurements containing both correct and abnormal data through iterative fitting.In contrast to the traditional least squares method that is susceptible to noise, the RANSAC algorithm progressively eliminates unqualified data, allowing it to provide faster and more accurate identification results for data samples containing a large number of noisy outliers.The RANSAC algorithm is often applied to detect regular objects in both images and point clouds.Our specific implementation process for extracting the off-site gravel point clouds is as follows.

(1) Step 1: a planar model was generated by randomly selecting three points from the point cloud space and forming a plane using these three points.

(2) Step 2: the distance from all other points to the plane was calculated, and an interior point was considered belonging to the same planar model if falling below a certain threshold, then the number of interior points under that model was recorded.

(3) Step 3: steps 1 and 2 were repeated.If points within the current model surpassed the maximum number of internal points saved, then the model parameters were updated.The saved model parameters represent the model with the highest number of internal points.

(4) Step 4: steps 1-3 were repeated, iterating through the parameters until reaching a specified iteration threshold.The model parameters containing the highest number of interior points was identified, then these interior points were used to estimate the model parameters again, yielding the final planar model parameters.

(5) Step 5: ground points were eliminated to obtain the off-site gravel point clouds.

The results of the RANSAC ground fit, as shown in Figure 4, exhibited residual noise points despite the fitting process.Further processing of the target point cloud was performed using radius filtering and color filtering.This additional step yielded multiple independent and less noisy gravel point clouds as the final result.

Fig.4 Process of eliminating ground points from original gravel point clouds (a) using the RANSAC algorithm(b), radius filtering (c) and color filtering (d)

The Euclidean distance-based algorithm is suitable for spherical clusters with similar size and density.However, in the case of gravels, each cluster can be arbitrarily shaped.To aggregate arbitrarily shaped clusters, Ester et al.(1996) proposed the DBSCAN algorithm.This algorithm utilizes the density of target points as the principle for clustering, dividing point cloud data into different clusters without the need to preset the number of clusters.The clustering results are independent of the traversal order of the points, and arbitrarily shaped clusters can be identified even in the presence of noise.

This algorithm does necessitate the pre-setting of two global parameters: the clustering radiusεand the minimum threshold of clustering density MinPts(number of points).With appropriately set parameters, the algorithm can effectively identify clusters of arbitrary shapes.The following basic definitions were utilized in the density clustering process.

(1)ε-neighborhood: for any given pointpin the set of pointss, the set of points within a distance ofεwithpas the center of the circle is defined as theε-neighborhood of the pointp.

(2) Core point: a pointpcis considered a core point if theε-neighborhood of the pointpccontains at least MinPtsnumber of sample points.

(3) Density direct: given a set of pointss, a pointqis considered density direct from a core pointpcifqis within theε-neighborhood of the pointpc.

(4) Density reachable: if forpcandq, there exists a chain of core pointspc1,pc2, …,pcn, andpc1topc2is density direct,pc2topc3is density direct, …,pc(n-1)topcnis density direct,pcntoqis density direct, thenpc1toqis density reachable.

(5) Density connected: pointspaandpbare considered density connected if there exists a pointpkthat is density reachable from both sample pointspaandpb.

The DBSCAN algorithm initially randomly searches for a core pointpc.It proceeds to identify all points connected to its density based onεand MinPts.These points are then labeled as a cluster.The algorithm selected the next unmarked point to derive the set of points connected to its density.The clustering process ceased after continuous iteration until no new points can be added to any cluster.At this point, the cluster labels containing noise were returned.

The color-filtered point cloud (Fig.4d) was input into the density clustering algorithm to identify clusters with various shapes.The result was a segmented gravel point cloud, as illustrated in Figure 5, where different colors represent different clusters.Evidently, the gravel point clouds are more accurately categorized in Figure 5, where the original irregular shapes were preserved more effectively.

Fig.5 Segmented gravel point cloud obtained using the DBSCAN algorithm.Each color represents a distinct gravel particle.

Individual gravels acquired through density clustering may exhibit outliers and noise points, a consequence of the abundant point cloud information obtained through multi-view reconstruction.Employing once statistical filter followed by twice guided filters effectively eliminated these noise points, enhancing the accuracy of subsequent calculations.Specifically, the noise points far away from the gravel can be removed by statistical filter; the surface of the point cloud can be smoother by guided filter with the noise points close to the gravels removed.The filtering schematic for a specific gravel particle (gravel number 15) is illustrated in Figure 6.

Fig.6 Filtering schematic for a specific gravel particle (gravel number 15).(a), initial point cloud with noise points after segmentation; (b), statistical filtered point cloud; (c), guided filtered point cloud.

2.4 Gravel measurements

2.4.1 Triaxial gravel grain size measurements

The study area can be mainly divided into erosion and stacked Gobi types.Different types exhibit distinct gravel characteristics.The grain size (mm) of gravel also reflects the material composition of the Gobi surface.In representing gravel grain size, the longest axis of the gravel was defined as theX-axis, the largest axis perpendicular to theX-axis as theY-axis, and the longest axis perpendicular to the plane containing theX-axis andY-axis as theZ-axis.

Manual measurements of grain sizes were conducted using a vernier caliper, with three measurements taken and averaged.The process of using regular geometry to enclose discrete points when identifying point cloud data is referred to as "solving the envelopment box".An algorithm can be used to determine the optimal bounding space for a collection of point clouds, covering box types including Spherical Box Axis-Aligned Box, Oriented-Bounding Box (OBB), and Discrete-Direction Polyhedral Box.

An OBB is the smallest rectangle that can encompass a target object in any direction.The OBB calculation process is relatively complex, but involves tightly encircling the target point cloud,potentially reducing an additional gap in space.Superior enclosure of the target and rotation invariance make the OBB a reasonable choice for extracting the spatial position of individual gravel point clouds.The lengths of the box's three sides were calculated to approximate the lengths of theX-,Y-, andZ-axis of the gravel particles.

2.4.2 Gravel volume measurements Gravel volume (mm3) was manually measured in this study using the drainage method.Initially, we washed and set aside the 34 gravel samples for subsequent measurement.Pure water was then introduced into a beaker (drainage cup).Upon reaching the drainage point, any surplus water flowed back into the beaker.Once the flow of pure water ceased, the beaker was weighed using a balance with a precision of 0.01 g, denoted asM1(Fig.7a).The gravel to be measured was then added to the drainage cup.As the pure water was displaced by the gravel and collected in the beaker, the combined weight was measured and recorded asM2(Fig.7b).The weight of the water expelled due to the introduction of gravel was determined asM2-M1.Based on the density of water (1 g/cm³), the displaced water's volume was equated to the measured volume of gravel.The averages of triplicate measurements were taken as the final volume measurements.The experimental apparatus is shown in Figure 7.

For regular 3D point cloud objects, volumes can be calculated using the geometric volume formula applicable to regular bodies.However, for irregular 3D objects, there is no fixed method.Common point cloud volume measurement methods include the voxel raster method, convex packet method, slicing method, and others.Examples of each method are provided in Figure 8.

Fig.7 Measurement of gravel volume using drainage method.(a), mass of the spilled water without the gravel;(b), mass of the spilled water with the gravel.

Fig.8 Schematic diagram of gravel volume measurements based on the gravel point cloud (a) using the voxel raster method (b), convex packet method (c), and slicing method (d)

The voxel raster method can be conceptualized as a 3D counterpart to the 2D pixel grid.In this representation, the point cloud is a cubic grid with certain specifications, the volume of which can be calculated by counting the number of occupied voxel grids within it.The convex packet method involves measuring the smallest convex envelope around the target point cloud that encloses all the point cloud data.The calculated volume of the convex packet of the point cloud is approximated as the volume of the enclosed 3D point cloud, making it suitable for determining the volume of convex objects.

Alternately, the slicing method involves computing volume by cutting the point cloud at equal intervals along the selected direction to obtain a series of discrete point cloud slices.The 3D coordinates of the sliced point cloud were obtained, and edge points were searched on the basis of the gradient of each point prior to an outer contour search.Finally, the slice area was calculated and the area of neighboring slices, along with the slice spacing, were determined as the volume of the approximate geometry.The results were cumulatively summed to determine the volume of the entire point cloud target.In this study, the above three methods were tested for effectiveness by comparison.

In the case of the slicing method, gravel volume was calculated as follows.

(1) Determining the slice distanceδ(mm): computing the average density of the point cloud and using three times the average density as the slice distanceδ.

(2) Data slicing: segmenting the point cloud in thez-direction according to the slice distanceδ.The final result is (Hz/δ)+1 slices, whereHz(mm) represents the height in thez-direction.

(3) Determining the boundary of the slice contour: obtaining the outer boundary of the contour by identifying the 2D convex envelope of the plane where the slice is located.

(4) Calculating the area of a single slice: computing the convex envelope area (S; mm2) using the Shoelace formula:

wheremis the number of convex envelope's vertices;xiandyirepresent the coordinates of theithvertex; andxi+1andyi+1represent the coordinates of the (i+1)thvertex.

(5) Volume calculation: summing each slice area to determine the volume of a single gravel point cloud.

2.5 Calculation of other 3D parameters

In addition to the grain size and volume of the gravel, various shape parameters were instrumental in determining 3D morphologies.The trajectory of sand particles colliding with gravels directly correlates with the gravels' 3D morphologies, subsequently influencing the physical properties of the Gobi surface.Currently, there is no dedicated measurement tool specifically tailored to capturing the 3D parameters of the gravel, and 2D images are insufficient for extracting 3D features.

In this study, the four parameters of triaxial grain size and volume of the gravel were used to calculate the flatness, roundness, sphericity, and equivalent grain size of the gravel.The formulas and descriptions of these parameters are given in Table 2.

Table 2 Description of 3D shape parameters of the gravel

As indicated in Table 2, upon acquiring the triaxial grain size of the gravel, the flatness information of the gravel could be directly computed.Flatness is a metric that reflects the shape of the gravel.In previous studies, parametric measurements for the gravel were relied on 2D projected images (typically for roundness), often defined as follows:

whereIis the roundness;At(mm2) is the projected area of the gravel particle andP(mm) is the perimeter of the particle projection.This definition only reflects 2D circularity.We utilized a 3D"grinding roundness" calculation method in this study, by taking into account the entire gravel surface area and triaxial grain size affecting roundness.

The gravel surface area (mm2) was estimated by triangulating the gravel point cloud.Sphericity served as a metric to gauge how closely a particulate matter resembles a sphere in 3D space,reaching its maximum value when a particulate matter has equal triaxial lengths, indicating a spherical shape.Conversely, sphericity is lower for flakes and columns.The sphericity information of gravels was calculated based on their volumes.

The equivalent grain size (mm) is a representation for irregular particles in comparison to homogeneous spherical particles with similar physical characteristics.In this study, the diameter of spherical particles was used as a representation of the diameters of the actual particles.For the same irregular particle, with reference to different physical parameters, more than one equivalent grain size value may be obtained.Relevant metrics included equivalent volume diameter,equivalent sinking velocity diameter, equivalent resistance diameter, equivalent projected area diameter, equivalent surface area diameter, and others.In this study, the equivalent volume diameter was selected as the representative size for gravel particles.

3 Results

3.1 Individual gravel grain size measurements

Manual measurements were compared with the point cloud measurements (Fig.9).The results revealed that the average absolute error ofX-axis was 1.08 mm with an average relative error of 5.88%.The average absolute error ofY-axis was 1.56 mm with an average relative error of 12.24%, and the average absolute error ofZ-axis was 0.92 mm with an average relative error of 11.44%.The average absolute error of the overall grain size was 1.19 mm, and the average relative error was 9.85%.Due to the subjective cognitive bias in axial diameter selection and the potential for errors in manual measurements using a vernier caliper, the results obtained from vernier caliper measurements may not fully and accurately represent the morphological parameters of gravels.Therefore, the vernier caliper measurement results were primarily utilized as reference data for the point cloud measurement results to assess the effectiveness of point cloud measurements.The results of the correlation analysis between the vernier caliper measurements of theX-,Y-, andZ-axis and the point cloud measurement results are illustrated in Figure 10.

Fig.9 Comparison between point cloud and manual measurements of the gravel grain sizes on X-axis (a), Y-axis(b), and Z-axis (c)

As depicted in Figure 10, the vernier caliper measurements of gravel grain sizes onX-,Y-, andZ-axis, all exhibited a strong positive correlation with the point cloud measurements of gravel grain sizes.The slopes of the linear fits were approximately 1.00 and the Pearson's correlation coefficients were 0.9937, 0.9645, and 0.9472 forX-,Y-, andZ-axis, respectively, all exceeding 0.9000.This suggests that the axial gravel grain sizes measured by OBB can effectively represent the true axial grain sizes of the gravel for subsequent data analysis.

Noisy points were inevitably generated during the 3D reconstruction process, and complete filtration of these points is challenging (Han et al., 2017).The presence of noisy points can enlarge the bounding box, resulting in an erroneously large grain size.For theZ-axis, the point cloud near the ground was lost due to the angle at which the image was taken during acquisition.This led to incomplete information for the bottom of the gravel, resulting in smallerZ-axis values measured from the gravel point clouds compared to those measured via vernier caliper.

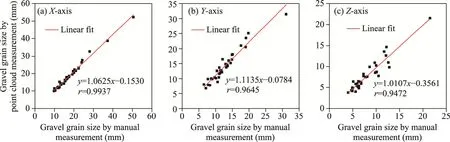
Fig.10 Linear fit results of the gravel grain sizes between point cloud and manual measurements on X-axis (a),Y-axis (b), and Z-axis (c).r, Pearson's correlation coefficient.

3.2 Individual gravel volume measurement results

The true volume of each gravel was measured using the drainage method, then the slicing method,convex packet method, and voxel raster method were employed to calculate its point cloud volume.A comparison of the calculation results is presented in Figure 11a.

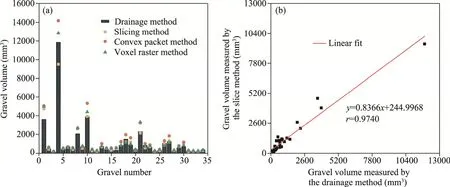
Fig.11 Gravel volume measured by the drainage method, point cloud slicing method, convex packet method, and voxel raster method (a) and linear fit result of the volume measured by the drainage method and the slice method (b)

The results indicated that the absolute errors of the measurements of the voxel raster, convex packet, and slice methods compared to the drainage method were 230.2, 362.3, and 217.8 mm3,respectively; the relative errors were 29.32%, 35.26%, and 21.23%, respectively.These results indicated that the slicing method is optimal.In the drainage method measurement, the volume of water was used as an approximate substitute for the gravel volume; the results readily diverged from the real values due to factors such as condensation in the experimental environment.We analyzed the correlation between the results of the drainage method and point cloud slicing method to assess the accuracy of the point cloud measurements, as illustrated in Figure 11b.The Pearson's correlation coefficient of the volume results measured by the drainage method and point cloud slicing method was as high as 0.9740, indicating a strong correlation between them.

3.3 Calculation results for other 3D parameters of individual gravels

Gravel flatness, as calculated based on vernier caliper measurements and point cloud measurements of the gravel triaxial grain size, is provided in Figure 12a.The proximity of the slope to 1.0000 indicates the degree of agreement between the point cloud measurements and vernier caliper measurements.The fitted slope for gravel flatness information was 1.0379, with Pearson's correlation coefficient exceeding 0.9000.This high correlation indicated that the point-cloud-reconstructed gravel particles align closely with the actual gravel particles, suggesting that representing gravel characteristics based on 3D point cloud calculations is feasible.

The distribution of gravel roundness and sphericity versus equivalent grain size measured by point cloud is shown in Figure 12b.Evidently, the gravel roundness and sphericity were not strongly correlated with equivalent gravel size in this case.

Fig.12 Linear fit of gravel flatness measured by point cloud and vernier caliper (a) and distribution of gravel roundness and sphericity versus equivalent grain size of different gravel particles measured by point cloud (b)

4 Discussion

Our results support the feasibility of point-cloud-based techniques in gravel measurements.Notably, the proposed technique affords comprehensive and 3D data for Gobi gravel analysis.Research gap related to dimensional richness and efficiency within the field of gravelly geodesy was addressed in this study, offering a novel perspective on geomorphological analysis.Through point cloud processing, we acquired not only 2D information about the gravel surface but also its 3D structures.This allowed for a more comprehensive understanding of the morphological characteristics of Gobi gravels, supplemented by additional measurements aiding in the more precise determination of gravel shapes, sizes, and spatial distributions (Masson et al., 2023).The efficiency and accuracy of the algorithmic framework employed in this study underscore the significance of point cloud technology in gravel surveying.

Additionally, we introduced a novel approach to conducting fine-grained analyses of gravel landforms.Compared with traditional image processing methods, the proposed algorithm not only excels in processing speed but also accuracy.The results of our experiments demonstrated the superiority of the point cloud technique in gravel measurements.This may have a far-reaching impact on academic research while supporting practical applications, such as geological exploration and environmental monitoring (Wu and Xu, 2014; Pan et al., 2020).The proposed method may be applicable in similar studies in the future, particularly in areas where highly detailed and precise gravel geomorphological analyses are required.

The equivalent grain size reflects the spherical nature of gravel (Clayton et al., 2009; Stahl and Konietzky, 2011).Figure 12 clearly illustrates a substantial deviation in the simulated Gobi gravels, which are highly complex in shape when using simplistic geometry.When simulating the 3D morphologies of Gobi gravels, an excessively simplified geometric model falls short in capturing authentic features.Consequently, simulation results may vary significantly between different studies (Elskamp et al., 2017) or substantially deviate from real-world conditions.Future research endeavors could focus on the development of more precise and adaptable models.These models should be designed to accurately represent the morphological intricacies of Gobi gravels,providing a robust foundation for further exploration in related fields.Such endeavors also may enhance the reliability and consistency of simulation outcomes in environments similar to Gobi.

However, there is still room for improvement in the future.Firstly, expanding the geographical range of samples could enhance the applicability of the results (Brasington et al., 2012).Secondly,future research could explore more flexible and sophisticated algorithms to manage complex terrains and irregular landforms more effectively.Future researchers could also leverage more precise equipment, or even multi-device collaborative work, to delve deeper into regions like the Gobi (Williams et al., 2020).While the algorithm utilized in this study demonstrated high accuracy, computational efficiency issues may arise with larger datasets.Future work could focus on optimizing the algorithm for scalability or exploring parallel computing methods (Liu and Boehm, 2015; Bao et al., 2021).With the insights gained from this study, future researchers can further advance the point cloud technique to explore a broader range of geological landforms and incorporate advanced techniques such as machine learning.

5 Conclusions

This study explored 3D parameter measurements for Gobi gravels based on point cloud technique.The key findings of this work can be summarized as follows.

(1) The method employed for generating gravel point clouds by 3D reconstruction of multi-view images is simple, fast, and cost-effective, with minimal disruption to the existing ground surface structure.Optimal shooting angles and methods were identified through the comparative analysis of various data acquisition schemes.This enabled the generation of point cloud files that not only encapsulate rich information but also exhibit a high level of fidelity in representing the actual gravel surface.

(2) The algorithm utilized in the point cloud processing workflow is easily implemented.From ground filtering to individual gravel segmentation and filtering, the algorithm ensures the preservation of information without loss.

(3) The automated measurements of individual gravels enabled calculation of their grain sizes and volumes.Importantly, the correlation coefficients between point cloud and manual measurements were above 0.9700 for grain size and volume measurement results.Overall, the proposed measurement scheme was proved to be straightforward, efficient, and informative.

(4) Through the grain size and volume parameters of gravels, their flatness, roundness, and sphericity were calculated.Gobi gravels, which are inherently complex in shape, cannot be adequately represented solely through geometric representations.Comprehending the shapes and dimensions of particles and interpreting them within the context of wear and crushing processes remain challenging issues and will necessitate sustained and extensive research efforts.

The utilization of 3D point clouds is an effective approach for investigating the irregular characteristics and morphologies of gravels.The measurement scheme implemented in this study was specifically tailored for studying the geomorphological features of gravels on the Gobi surface, offering significant savings in terms of manpower and material resources during field investigations.This method may contribute to a standardized characterization of gravel morphologies, thereby creating a more robust database for understanding the development and formation of the Gobi region, as well as comprehending wind-sand effects and promoting environmental protection efforts.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was funded by the National Natural Science Foundation of China (42071014).We are grateful to the editors and anonymous reviewers for their insightful comments and suggestions in improving this manuscript.

Author contributions

Conceptualization: JING Xiangyu, HUANG Weiyi, KAN Jiangming; Investigation: JING Xiangyu, HUANG Weiyi, KAN Jiangming; Data curation: JING Xiangyu, HUANG Weiyi; Funding acquisition: KAN Jiangming;Methodology: HUANG Weiyi, JING Xiangyu; Visualization: JING Xiangyu, HUANG Weiyi; Writing - original draft preparation: HUANG Weiyi, JING Xiangyu; Writing - review and editing: JING Xiangyu, KAN Jiangming.All authors approved the manuscript.