Urban growth scenario projection using heuristic cellular automata in arid areas considering the drought impact
2024-04-22TANGXiaoyanFENGYongjiuLEIZhenkunCHENShuruiWANGJiafengWANGRongTANGPanliWANGMianJINYanminTONGXiaohua
TANG Xiaoyan, FENG Yongjiu*, LEI Zhenkun, CHEN Shurui, WANG Jiafeng,WANG Rong, TANG Panli, WANG Mian, JIN Yanmin, TONG Xiaohua
1 College of Surveying & Geo-Informatics, Tongji University, Shanghai 200092, China;
2 Shanghai Key Laboratory of Space Mapping and Remote Sensing for Planetary Exploration, Tongji University, Shanghai 200092, China
Abstract: Arid areas with low precipitation and sparse vegetation typically yield compact urban pattern,and drought directly impacts urban site selection, growth processes, and future scenarios.Spatial simulation and projection based on cellular automata (CA) models is important to achieve sustainable urban development in arid areas.We developed a new CA model using bat algorithm (BA) named bat algorithm-probability-of-occurrence-cellular automata (BA-POO-CA) model by considering drought constraint to accurately delineate urban growth patterns and project future scenarios of Urumqi City and its surrounding areas, located in Xinjiang Uygur Autonomous Region, China.We calibrated the BA-POO-CA model for the drought-prone study area with 2000 and 2010 data and validated the model with 2010 and 2020 data, and finally projected its urban scenarios in 2030.The results showed that BA-POO-CA model yielded overall accuracy of 97.70% and figure-of-merits (FOMs) of 35.50% in 2010,and 97.70% and 26.70% in 2020, respectively.The inclusion of drought intensity factor improved the performance of BA-POO-CA model in terms of FOMs, with increases of 5.50% in 2010 and 7.90% in 2020 than the model excluding drought intensity factor.This suggested that the urban growth of Urumqi City was affected by drought, and therefore taking drought intensity factor into account would contribute to simulation accuracy.The BA-POO-CA model including drought intensity factor was used to project two possible scenarios (i.e., business-as-usual (BAU) scenario and ecological scenario) in 2030.In the BAU scenario, the urban growth dominated mainly in urban fringe areas, especially in the northern part of Toutunhe District, Xinshi District, and Midong District.Using exceptional and extreme drought areas as a spatial constraint, the urban growth was mainly concentrated in the "main urban areas-Changji-Hutubi"corridor urban pattern in the ecological scenario.The results of this research can help to adjust urban planning and development policies.Our model is readily applicable to simulating urban growth and future scenarios in global arid areas such as Northwest China and Africa.
Keywords: bat algorithm; cellular automata (CA); probability-of-occurrence; drought intensity;algorithm-probability-of-occurrence-cellular automata (BA-POO-CA) model; arid areas
1 Introduction
Exploring and understanding urban growth in arid areas is crucial to sustainable urban development,especially in Northwest China and Africa (Huang et al., 2019; Govind and Ramesh, 2020).Cities in arid areas are prone to drought, sandstorms, and other natural hazards due to scarce precipitation and sparse vegetation (Middleton and Sternberg, 2013).Research findings indicated that urban growth was more sporadic and episodic in drought-prone areas and more stable in irrigated areas (Lawrence et al., 2022).In Africa, urban development was constrained by the impact of drought, affecting crop growth and thus leading to urban poverty (Shimada, 2022).Under the effect of drought-related adverse conditions, there is an urgent need for spatially explicit pixel-level simulations of how urban growth processes and future scenarios will evolve.The dynamic simulation should improve our understanding of urbanization and provide effective support for sustainable urban planning (Kumar et al., 2021).Cellular automata (CA) models are typically an effective framework for modeling the spatiotemporal evolution of complex geographic phenomena such as urban growth (Mozaffaree Pour and Oja, 2021).Although CA models have been applied worldwide to simulate future urban scenarios, more applications have been performed in densely populated areas and coastal areas, while less attention has been given to sparsely populated arid areas (Wu et al., 2018; Zhang et al., 2020; Lü et al., 2021; Li et al.,2022b).Therefore, one of the current challenges of CA research is to construct more appropriate simulation models for urban growth in arid areas considering the arid climate and special development context.
Modeling urban growth with CA models depends on their transformation rules predefined by a variety of methods such as statistical regression, fuzzy logic, decision tree, and artificial intelligence (Ke et al., 2016; Mirbagheri and Alimohammadi, 2017; Huang and Liao, 2019).Heuristics are common assemblies of artificial intelligence methods that have been increasingly applied to CA modeling for urban growth, and typical algorithms include general-purpose heuristics, evolutionary heuristics, and swarm heuristics (Civicioglu and Besdok, 2013; Naghibi et al., 2016).For heuristics, there are two ways to establish transformation rules: (1) automatically finding CA parameters to produce a probability-of-occurrence (POO) map for urban growth; and(2) building massive "IF....THEN" form of transformation rules, which are used to calculate each cell successively.For the first way, by searching for the smallest modeling error and thus the best CA parameters, the heuristics allow the construction of suitable transformation rules and improve simulation accuracy (Feng and Tong, 2018).For the second way, "IF....THEN" rules are direct criteria for cell state transformations, while heuristics have advantages in mining such rules (Cao et al., 2019).For example, Cao et al.(2016) applied a heuristic bat algorithm (BA) to derive "IF....THEN" rules and constructed a bat algorithm-cellular automata (BA-CA) model to simulate the urban growth of Nanjing City, Jiangsu Province, China.However, CA models based on different heuristics yield different simulation results and are applicable to different areas, as a result of the wide variety of heuristics and differences in control parameters.
Modelers have developed and validated different CA models for urban growth around the world, where models for fast-growth or low-growth areas, as well as models for coastal areas or arid areas, are not applicable universally (Kamusoko and Gamba, 2015; Naghibi and Delavar,2016; Gao et al., 2020; Ding et al., 2022).The rapidly developing regions of China, such as Beijing-Tianjin-Hebei, the Yangtze River Delta, and the Pearl River Delta, are rich in resources and have a friendly climate, and their urban growth patterns are different from those in Northwest China (Liu et al., 2018; Dong et al., 2020).Thus, although there are many CA models in the literature to elaborate on land use change and urban growth in these areas, these models still need to be modified when applied to the arid and relatively slow-growing areas in Northwest China.The arid areas of Northwest China have two main characteristics: (1) the topography is highly undulating and mostly desert, which may lead to a greater contribution of topographic factor to CA models; and (2) the degree of drought caused by low precipitation and high evaporation is an important factor in the modeling for urban growth.These indicate the importance of developing appropriate CA models for cities in arid areas and exploring the spatiotemporal pattern of urban growth in Northwest China to improve the cities' production concentration and carrying capacity(Maimaiti et al., 2021).
On this regard, research on CA model construction and urban scenario prediction for typical cities in Northwest China, such as Lanzhou City, Xining City, Yinchuan City, and Urumqi City,needs to be greatly enhanced.Here, we posed three research questions: (1) can heuristics be applied to simulate urban growth in typical arid areas? (2) can the inclusion of drought factors in CA models more accurately simulate urban growth in arid areas? and (3) can this new CA model predict future scenarios for arid cities in Northwest China (e.g., Urumqi City)? The answers to these questions would enhance the CA modeling system and our understanding of urban evolution in arid areas, especially in the arid areas of Northwest China.The heuristic BA proposed by Yang(2011) can effectively improve the convergence speed while searching for the globally optimal solution.Hence, we adopted this algorithm to construct CA model and use frequency tuning techniques to increase the diversity of solutions in the population to realize the fast convergence of CA parameter search.The new model was named bat algorithm probability- of-occurrence cellular automata (BA-POO-CA) and developed under the UrbanCA environment (Feng and Tong,2019), which also applies a time-increasing parameter and a local-adjustment parameter to produce POO map.Urumqi City is at the intersection of the China-Central Asia-West Asia Economic Corridor, China-Mongolia-Russia Economic Corridor, and China-Pakistan Economic Corridor, and has a crucial position in China's all-round opening scheme (Fu et al., 2021).We calibrated this BA-POO-CA model for Urumqi City by the data of 2000 and 2010, validated the model by the data of 2010 and 2020, and then projected future scenarios for the city in 2030.In the modeling, to identify the contribution of drought factors, we compared the BA-POO-CA model excluding drought intensity factor with the BA-POO-CA model including drought intensity factor in terms of simulation accuracy and urban pattern.Through this study, we endeavored to develop new approaches to simulate urban growth in arid areas and to enable their extension to a wider range of arid areas.
2 Methods
2.1 Study area and datasets
Urumqi City is a typical arid city in Northwest China, and the study of its urban growth can provide a reference for optimizing the functional layout of cities in such regions.Given that our focus is on the urban growth of cities in arid areas, our study area is Urumqi City and its surrounding areas, where urban growth is more pronounced (Fig.1).The city is the capital of Xinjiang Uygur Autonomous Region in Northwest China and an international business center for Central and West Asia.Urumqi City has a continental temperate climate with a large diurnal temperature difference and low precipitation.With an average annual precipitation of 236 mm,the city's evaporation is much greater than its precipitation, resulting in sparse vegetation; thus,drought is a major constraint to its urban growth (Fig.1a).The city is surrounded on three sides by mountains, with a high southeast and low northwest topography.The population of the city was 4.08×107in 2023, of which more than 90.00% were urban residents.Urumqi City consists of seven districts, including Dabancheng District, Midong District, Saybagh District, Shuimogou District, Tianshan District, Toutunhe District, and Xinshi District, and one county (Urumqi County), with a total area of 13,800.0 km2.The Xinshi District, Tianshan District, and Saybagh District are the centers of the city (Fig.1b).Over the past two decades, land use in Urumqi City has shown moderate changes, but not as much in developed coastal cities in China (Zhang et al.,2022a).
Urban growth is influenced by many factors, including socioeconomic, natural, and environmental aspects (de Jong et al., 2021; Surya et al., 2021).Among these, we selected widely used factors (e.g., proximity) and typical factors (e.g., drought intensity) to construct CA models for future urban growth simulations and projections.We generated factor layers for CA modeling using vector dataset maps and satellite imagery (Table 1).As a topographic feature, the Shuttle Radar Topography Mission Digital Elevation Model (SRTM DEM) was used to calculate land elevation to assess its impact on land use change.Expressway networks representing traffic features at a scale of 1:500 were used to extract spatial proximity.The location factors including city center and town centers were included to extract the effects of their spatial proximity.Since the study area is located in an arid area, several factors related to environment, including drought intensity, normalized difference vegetation index (NDVI), and soil moisture, were incorporated to assess their effects on urban growth.Considering land surface temperature, NDVI, potential evapotranspiration, and soil moisture as four factors, we derived drought intensity using the entropy weight method based on Moderate Resolution Imaging Spectroradiometer (MODIS) products and Sentinel-1A imagery (Tang et al., 2023).In addition, the socioeconomic factors such as population per pixel (PPP) and gross domestic product (GDP) were also included in the modeling.
To analyze historical urban growth, we used multiple land use data at 30 m resolution from the GLC_FCS30 product (Zhang et al., 2021) as inputs to calibrate the CA model from 2000 to 2010 and validate the model from 2010 to 2020.GLC_FCS30 provides accurate public land use data products, with an official overall accuracy of 82.50% and a kappa coefficient of 0.784 (Zhang et al., 2021), and the literature shows that GLC_FCS30 has an overall accuracy of 90.80% (Zhai et al., 2023).Furthermore, the data product provides more spatial details and performs well in reflecting complex urban details, especially in arid land (Bie et al., 2023; Shi et al., 2023).The initial GLC_FCS30 dataset comprises 29 land categories, which have been merged into urban,non-urban, and excluded (water body) due to the focus of this study on urban growth modeling.Specifically, we resampled the drought intensity, NDVI, soil moisture, PPP, and GDP data to 30 m resolution using bilinear resampling in ArcMap (Environment System Research Institute,Redlands, California, the USA).Given the inherent imprecision of these data, the differences between coarse resolution and resampled fine resolution datasets were not substantial, thereby not leading to significant errors in the modeling results.Resampling facilitated the CA's iterative calculations by ensuring uniform pixel size.All spatial factors were normalized to remove the effect of dimensionality on land use modeling (Fig.2).Prior to building the transformation rules,the contribution of factors was assessed using a generalized additive model (GAM) to quantify their ability for explaining urban growth.

Table 1 Description of the selected factors to construct cellular automata (CA) model for analyzing urban growth in the study area
2.2 Model workflow
Figure 3 illustrates how CA parameters were optimized using BA to develop dynamic urban growth models suitable for arid areas.These factors were categorized into two groups, one excluding drought intensity factor (digital elevation model (DEM), Euclidean distance to expressway (D_expressway), Euclidean distance to city center (D_city), Euclidean distance to town center (D_town), NDVI, soil moisture, PPP, and GDP) and the other including drought intensity factor (DEM, D_expressway, D_city, D_town, drought intensity, NDVI, soil moisture,PPP, and GDP).A systematic sampling method was used to derive training samples from land use maps (2000 and 2010) and the factor layers (i.e., the two groups above).There is necessarily a difference between the actual and modeled land use change, which can also be considered a modeling error.This error can be written as an objective function, which is equivalent to projecting the modeling space to BA algorithm space.Based on objective function, we can find the best CA parameters by using BA and searching for the minimum modeling error to produce the POO maps of BA-POO-CA models.Two BA-POO-CA models were calibrated by the two groups of factors (i.e., excluding and including drought intensity factor).The models were applied to project two different scenarios of urban growth for Urumqi City in 2030.Modeling was performed in our previously developed UrbanCA software (Feng and Tong, 2019), which is available to users worldwide.
2.3 Basic urban CA model
CA model can be conceived as a state-determined model consisting of a cell space and a transformation function, which defines the POO of urban growth.In CA models, the land transformation rule is determined by a combination of five elements including cell states, POO,neighborhood effects, constraints, and randomness (García et al., 2013).The CA transformation rule can be expressed as (Wu, 2002; Lei et al., 2022):
whereStiandSit1+are the states of celliat time steptandt+1, respectively;Tranis the transformation function;Pparis the temporally static POO calculated using driving factors;Nis the effect of neighboring urban cells on the central cell;Cis the prohibited area due to unsuitable conditions or urban planning regulations; andRis a random disturbance that models any unknown perturbation.
The temporally static POO determined by spatial driving factors (Ppar) can be given by Equation 2 (Munshi et al., 2014; Jafari et al., 2016):

Fig.2 Spatial distribution of normalized factors selected to simulate the urban growth of study area.(a), DEM(digital elevation model); (b), D_expressway (Euclidean distance to expressway); (c), D_city (Euclidean distance to city center); (d), D_town (Euclidean distance to town center); (e), drought intensity; (f), NDVI (normalized difference vegetation index); (g), soil moisture; (h), PPP (population per pixel); (i), GDP (gross domestic product).
wherea0is a constant;xzis thezthdriving factor of urban growth;azis the weight of factorxz;nis the total number of driving factors; andεis the modeling residual.
We used an addition operation to calculate the overall POO (Pall), by taking into account the changes in both POO and neighborhood during simulation.ThePallcan be given by Equation 3(Feng and Tong, 2019):
whereSTIPis a time-increment parameter to resist the decaying effect of local POO at time stept-1; andSLAPis a local adjustment parameter to reduce the enhancement of neighborhood effects.

Fig.3 Workflow diagram of bat algorithm-probability-of-occurrence-cellular automata (BA-POO-CA) models for simulating urban growth dynamic in arid areas
Smaller modeling residuals correspond to the optimal CA parameters, which are ultimately used to establish appropriate transformation rules and thus improve simulation accuracy.To derive the CA parameters while minimizing the model's residuals, we constructed an objective function as:
whereF(w)is the objective function;wis a feasible solution of CA parameters;Ppar(w)is the predicted POO;P0is the observed urban growth; andmis the number of samples.
2.4 BA-POO-CA model
To solve the objective function, we adopted BA method for the iterative search of optimal solution first proposed by Yang (2011).Supposing there aresminiature bats in ad-dimensional search space, where each dimension corresponds to a factor influencing urban growth and each miniature bat contains a feasible set of CA parameters.The code of miniature bats can be defined as:
whereXjis the code ofjthminiature bat (j=0, 1, …,s);Ajis the position ofjthminiature bat (i.e.,thejthCA parameter);vjis the velocity ofjthminiature bat;fjis the frequency ofjthminiature bat;andLjis the loudness ofjthminiature bat.
BA is a distance-aware method for echolocation of miniature bats via idealized rules for optimization problems.Miniature bats fly randomly with velocity (vj), frequency (fj) and different loudness (Lj) at position (Aj) in search of their prey.The velocity is dynamically updated according to the changing frequency.The movement ofjthminiature bat updating its position (Aj)and velocity (vj) in the search space can be defined by Equation 6 (Yang, 2011):

In accordance with the proximity of target, the loudness (Lj) varies from a maximumL0to a minimum constantLminand is updated accordingly with the number of iterations.The loudness usually decreases when the bat finds its prey, and assumingLmin=0 means that the bat has just found its prey and temporarily stops making any sound, thus the update of the loudness (Lj) can be given by Equation 7 (Yang, 2011):

whereδis a vector of random numbers between [-1, 1]; andLtis the average loudness of allsminiature bats at time stept.
2.5 Validation procedure
We calibrated BA-POO-CA models using land transformation rules derived from urban growth from 2000 to 2010, and then validated the models by simulating the final state of study area in 2020.Based on earlier publications (Feng and Tong, 2019), we setSTIPto 0.01,SLAPto 0.8, and the neighborhood to a 5×5 square cell.By comparingPallof each land cell with a predefined thresholdPthd, the cell's future statecan be determined.IfPall>Pthd, the land cell is converted to urban state; otherwise, the original state is maintained.We experimented with different thresholds and simulated the urban pattern under these thresholds until the difference between the predicted and actual urban cells was smaller than 1.00%, and finally the threshold and its corresponding simulation results were considered valid.
2.6 Model evaluation methods
To evaluate the simulation results, we calculated the error matrix based on cell-by-cell comparison between actual patterns from remote sensing imagery and simulated patterns from BA-POO-CA models (Tong and Feng, 2020).The error matrix reported three metrics including overall accuracy,kappa coefficient, and figure-of-merits (FOMs).Besides, we selected eight landscape-level metrics commonly used to measure the similarity and variability of simulated urban patterns(McGarigal et al., 2015; Nadoushan and Alebrahim, 2017).These metrics included the number of patches (NP), largest patch index (LPI), perimeter-area fractal dimension (PAFRAC), contagion(CONTAG), landscape division index (DIVISION), splitting index (SPLIT), Shannon's diversity index (SHDI), and Shannon's evenness index (SHEI).
3 Results
3.1 Observed urban growth pattern
To analyze the urban growth of the study area, we merged various types of GLC_FCS30 data for the years of 2000, 2010, and 2020, including three categories: urban (impervious surfaces),non-urban (areas other than impervious surfaces and water body), and excluded (water body) (Fig.4).Since water body is considered to be relatively stationary, we considered it as spatial constraint.Between 2000 and 2010, urban growth in the study area occurred mainly in low-lying areas close to existing built-up areas, showing an encircling expansion (Fig.4d).Over the past two decades, the urban growth of the study area occurred mainly in Xinshi District, Tianshan District, Saybagh District, and the surrounding low-lying areas, showing a distinct agglomeration pattern.Of these, the urban growth of study area during 2010-2020 was found mainly in the northeast and southwest of the initial built-up areas, showing a discrete pattern of urban growth that the built-up area is less dense than the city center.From 2000 to 2010, the study area experienced relatively rapid urban growth, urban land increased from 552.3 to 797.8 km2with a growth rate of 44.50%; from 2010 to 2020, urban land continued to expand, but at a slower growth rate of 28.30% (Fig.4e).
3.2 Model calibration
The control parameters of heuristics are crucial to implement the search for optimal solution.Since BA is a heuristic, a smaller population may lead to locally optimal solutions, while a larger population will lead to a heavy computational load.In this study, we specified the parameternumPopulationas 20 times the number of variables in BA-POO-CA models according to earlier literature (Feng and Tong, 2018).The default control parameters recommended in R package (R Foundation for Statistical Computing, Vienna, Austria) of BA heuristic were used for maximum frequency, minimum frequency, pulse rate, and loudness (Table 2).These parameters were determined by software publisher after extensive testing.The lower bound of positive parameters and the upper bound of negative parameters were both set to zero, while the upper bound of positive parameters and the lower bound of negative parameters were given as twice the parameters derived from logistic regression (Feng and Tong, 2018).
As shown in Figure 5, the two function values of BA decreased very rapidly in the early stage of optimization process and converged after 1500 generations.As the difference between the two function values became smaller than acceptable tolerance (1.00×10-6), the BA optimization operation was terminated at predetermined number of iterations (5000 generations in this study)and the final optimal function values of BA excluding and including drought intensity factor were 0.09825 and 0.09697, respectively.
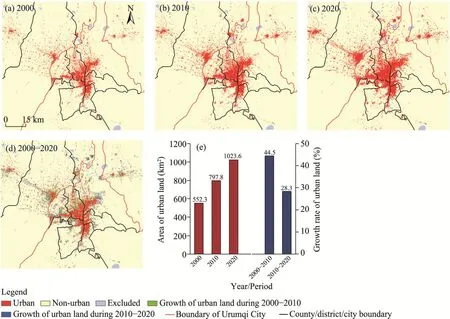
Fig.4 Urban pattern of the study area in 2000 (a), 2010 (b), and 2020 (c) and urban growth pattern during 2000-2020 (d), as well as the growth of urban land area from 2000 to 2020 (e)

Table 2 Control parameters of bat algorithm (BA) heuristic for retrieving CA transformation rules
Figure 6 shows the POO maps and CA parameters retrieved using BA-POO-CA model excluding and including drought intensity factor, with POO ranging from 0 to 1.Overall, the two POO maps were highly similar, yet they displayed differences in localized areas (Fig.6a and b).Visual inspection suggested that the land around existing urban centers was more suitable for development, and the POO value of excluding drought intensity factor was slightly lower than that of including drought intensity factor, suggesting that the former group may simulate less urban growth.The two POO maps excluding and including drought intensity factor were produced by the CA parameters retrieved using BA (Fig.6c and d).Except for GDP and PPP, the negative values parameters indicate a promoting effect on urban growth, positive values indicate an inhibiting effect on urban growth, and the magnitude of absolute values indicate the influencing degree of corresponding factors on urban growth.For BA-POO-CA model considering drought intensity, D_city, DEM, and D_expressway were the three most important influencing factors in descending order (Fig.6d).We assessed the contribution of each factor to BA-POO-CA model using a generalized additive model, which reports the ranking of factors (Fig.6e and f).To calibrate CA transformation rules, we selected 9964 samples from the 2000 initial map, 2010 final map, and all factor maps using systematic sampling.These factors were categorized into two groups: excluding drought intensity factor and including drought intensity factor.The POO maps and CA parameters with excluding or including drought intensity factor retrieved by BA were used to construct CA models to simulate urban pattern in 2020 and to project future urban growth in 2030.
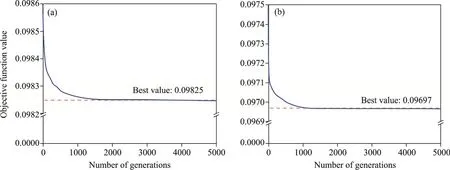
Fig.5 Convergence process of BA for optimizing BA-POO-CA models excluding (a) and including (b) drought intensity factor in the study area
3.3 Simulated results
Based on the two POO maps, we simulated the urban patterns in 2010 and 2020, which show that urban growth from 2000 to 2020 occurred primarily in areas around the city center of Urumqi City (Fig.7).The city showed a triangular urban form with a tendency of expanding to the northwest.The simulated urban areas by BA-POO-CA model excluding and including drought intensity factor in 2010 were 790.9 and 795.4 km2, respectively (Fig.7a and c), and those were 1012.6 and 1014.7 km2in 2020, respectively (Fig.7b and d).Simulation results based on these two models were similar in the overall pattern, but there were local differences, where the simulation results of model excluding drought intensity factor were more dispersed than those of model including drought intensity factor.This suggested that the absence of drought intensity constraint would provide more alternative sites for urban development.
3.4 Model validation
Figure 8 shows the assessment maps that demonstrate mainly the hit, miss, and false alarm for 2010 and 2020.The enlarged areas showed that the correct simulations typically occurred near the initial urban areas while the false alarms occurred in suburbs, and the missing area was usually near the correctly hit cells.The assessment maps of the two models were similar in overall pattern but different in the localized pattern, and visual inspection showed that the simulation patterns with drought intensity factor have more correct simulations in the second enlarged area in 2010 and 2020.These suggested that BA-POO-CA model including drought intensity factor had a stronger ability to capture urban growth in arid areas.
We compared the simulated urban growth from 2010 to 2020 with the actual situation in pixel-by-pixel and evaluated the simulation results (Table 3).The overall accuracy of simulated urban patterns for both 2010 and 2020 exceeded 97.50%.The BA-POO-CA model including drought intensity factor captured 1.00% from 1.80% actual urban growth in 2010 and 0.80% from 1.60% actual urban growth in 2020, resulting in a modeling capacity of 55.56% and 50.00% for 2010 and 2020, respectively.For both 2010 and 2020, the FOMs for BA-POO-CA model including drought intensity factor were significantly higher (by 5.50% and 7.90%, respectively)than the model excluding drought intensity factor.These suggested that BA-POO-CA model including drought intensity factor better reflected urban growth dynamic in arid areas than other models.
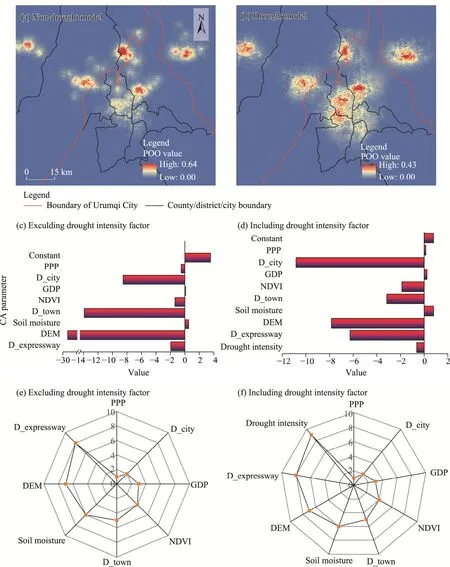
Fig.6 POO maps (a and b), values of CA parameter (c and d), and rank of factor contribution (e and f) of BA-POO-CA model excluding and including drought intensity factor
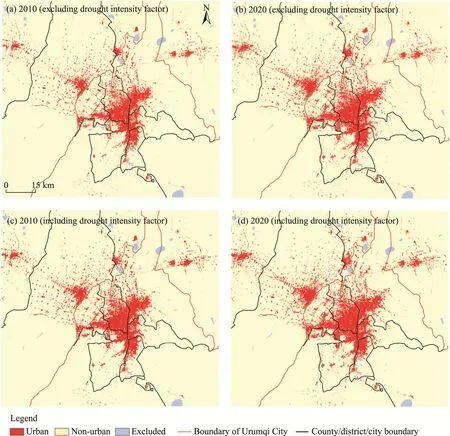
Fig.7 Simulated urban growth pattern by BA-POO-CA model excluding (a and b) and including drought intensity factor (c and d) in 2010 and 2020
To further compare the urban patterns simulated by the two BA-POO-CA models, we calculated eight landscape-level metrics using FRAGSTATS 4.2 (Department of Environmental Conservation, University of Massachusetts, Massachusett, the USA) and assessed the differences and similarities between the simulated results in terms of area-edge, shape, aggregation, and diversity (Table 4).The two types of simulation results didn't differ significantly in terms of landscape-level metrics, but the simulation results produced by BA-POO-CA model including drought intensity factor were more similar to the observed patterns.The increased NP metric for both observations and simulations suggested that the urban pattern of Urumqi City has become more complex over time.The BA-POO-CA model excluding drought intensity factor had a higher LPI compared with the model including drought intensity factor, indicating that the former model produced larger urban patches and more complex landscape patterns.The CONTAG metric also indicated that the BA-POO-CA model excluding drought intensity factor produced a higher degree of landscape connectivity and aggregation than the other model.The BA-POO-CA model including drought intensity factor produced a higher degree of landscape separation as indicated by DIVISION and SPLIT metrics, and a higher degree of fragmentation as indicated by SHEI metric.
3.5 Future scenarios
The BA-POO-CA model including drought intensity factor was applied to project urban scenario for 2030 under two conditions, that is, Scenario-I: the business-as-usual (BAU) scenario and Scenario-II: an ecological scenario that emphasizes the impact of drought on urban growth (Fig.9).
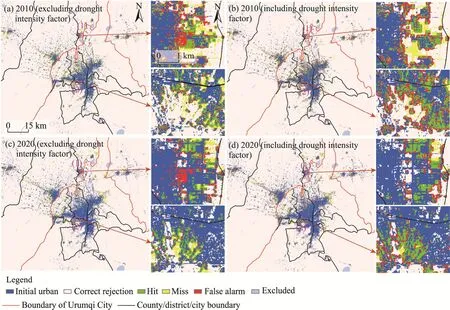
Fig.8 Assessment results of urban growth pattern simulated by BA-POO-CA model excluding (a and c) and including (b and d) drought intensity factor in 2010 and 2020.Hit represents the urban growth area for both actual and simulation pattern; miss represents the actual urban growth area but simulated non-urban area; false alarm represents the actual non-urban area but simulated urban growth area; and correct rejection represents non-urban area for both actual and simulation pattern.
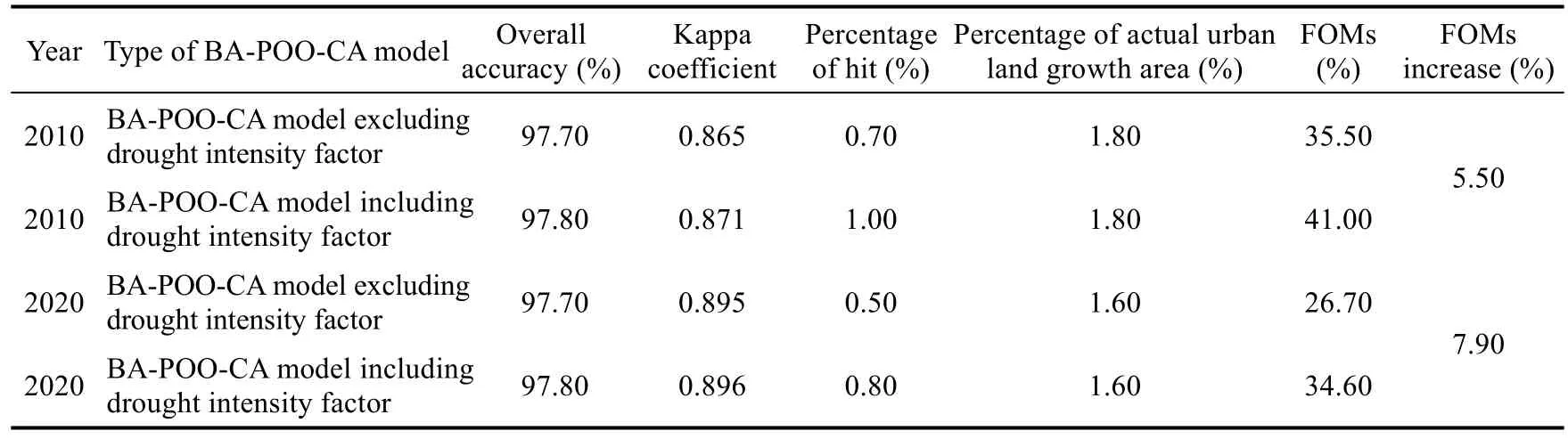
Table 3 Accuracy of simulation pattern produced by BA-POO-CA model
Scenario-I assumed the same growth rate of urban land in the study area as in the previous period, without taking into account changes in policies, infrastructure improvements, and economic conditions.In this scenario, the urban growth dominated mainly in urban fringe areas,especially in the northern part of Toutunhe District, Xinshi District, and Midong District.Fukang City and Wujiaqu City also emerged significant urban growth (Fig.9a).Scenario-II considered drought as the most important environmental factor constraining urban growth in arid areas, then used exceptional and extreme drought areas as restricted areas for urban development, and finally shifted urban growth to areas not constrained by drought.Under this scenario, few urban growth cells occurred in the areas around the core urban areas of Urumqi City but more occurred along the Changji City-Hutubi County direction, leading to the "main urban areas-Changji-Hutubi"corridor urban pattern (Fig.9b).In this scenario, the impact of drought on the urban growth of Urumqi City was considered, and the urban drought situation could be expected to mitigate.Overall, the two urban growth patterns lead to two different urban scenarios, which are good recommendations for urban planning and policy implementations.

Table 4 Results of landscape-level metrics of observed and simulated urban patterns

Fig.9 Urban pattern of the study area in 2030 projected by BA-POO-CA model.(a), scenario I (BAU scenario);(b), scenario II (ecological scenario).
4 Discussion
The most influential factor of urban development in arid areas is drought, resulting in different population carrying capacities and therefore different city sizes and morphology (Vicente-Serrano et al., 2020; Zhang et al., 2022b).Accordingly, when modeling urban growth dynamic of cities in arid areas like Urumqi City, it is essential to consider not only historical land use change and the relevant socioeconomic factors, but also environmental factors (Chaturvedi and de Vries, 2021;Jayasinghe et al., 2021; Mozaffaree Pour and Oja, 2021).Meanwhile, the simulation methods are equally important in capturing urban conditions and projecting future urban scenarios (Liang et al.,2018; He et al., 2022); for example, heuristics are a class of methods that allow capturing multi-objective results with physically meaningful parameters.Hence, for land use change and urban growth in arid areas, the selection of modeling factors and the optimization of modeling methods are important for projecting future multiple scenarios and thus urban development policy formulation.
4.1 Impact of factor selection on modeling
The selection of factors influencing urban growth affects the accuracy of modeling, and factors with different features would lead to different model simulation results.Among these,topographical conditions, environmental conditions, and human activities are generally recognized as the main drivers of urban development, which can reflect the mechanisms of urban growth in different regions (Li et al., 2018).In contrast to the factor selection influencing urban growth of economically developed coastal cities that had focused mainly on environmental and human activities factors (Wang et al., 2021; Zhai et al., 2021; Li et al., 2022b), we examined the key climatic factors affecting the arid areas of Northwest China.Although topographic and socioeconomic factors have been widely used (Li et al., 2022a; Yang et al., 2023), they may not well reflect the dynamics of urban growth in arid areas.In the urban areas of Northwest China where precipitation is low, sunshine duration is long, and evaporation is high (Yang et al., 2022),we therefore selected drought intensity as one of the important factors for urban growth.We conducted simulation experiments with two groups of drivers including and excluding drought intensity factor to test whether this factor could improve the simulation accuracy.Our results showed that the group of factors that include drought intensity factor had higher FOMs,suggesting that this factor can better characterize the urban growth in arid areas and contribute to the improved simulation accuracy.Therefore, it is appropriate that we included drought intensity factor as one of factors in this study.
In addition, factors with multifaceted characteristics can more appropriately reflect the urban growth in arid areas (Dahal and Lindquist, 2018; Seevarethnam et al., 2022).Although many factors have been found to be associated with urban growth, simulation modeling may be subject to factor multicollinearity and data redundancy due to correlation among factors (Bayer Altin and Altin, 2021).Therefore, in this study, we have selected a representative group of nine factors covering topographic, locational, socioeconomic, and environmental characteristics.Urban growth is a complex phenomenon, so its modeling requires the selection of time-matched factors (Feng et al., 2019), and most of these factors can be acquired using remote sensing techniques.There is always uncertainty in remote sensing data, which may affect the ability to capture urban growth characteristics over time.
4.2 Impact of heuristic parameterization on modeling
Heuristics are categorized differently depending on the solution methods, such as general heuristics, evolutionary heuristics, and swarm heuristics (Civicioglu and Besdok, 2013; Naghibi et al., 2016), and these algorithms have different applicability in simulations.The control parameters of heuristics are crucial to achieve the optimal solution search.Since different solution techniques are used for the optimization problem, different heuristics have different control parameters that directly affect the final parameter solutions (Cao et al., 2019; Li et al., 2022c).Therefore, the extensive calibration of these parameters should lead to better models.The loudness variable in BA method used in this study provides an automatic scaling capability,effectively improving the convergence speed by making the search process denser as it approaches global optimization.Meanwhile, BA controls the speed and range of bat population's movement through frequency, thus guiding it to the optimal solution.To some extent, BA can be perceived as a balanced combination of standard particle swarm optimization and dense local search controlled by loudness.In our simulation studies, we used the default control parameters recommended by BA in the R package, which were determined after intensive testing by the software publisher, and we eventually acquired the optimal solution.
In CA modeling, we projected the actual problem of urban simulation to the space of heuristics using the modeling residual minimization function, i.e., the objective function.Therefore, in this study, we automatically identified CA parameters by searching for the minimum modeling error,and these parameters can explain each factor's contribution to urban growth in arid areas.Finally,we produced the POO maps of urban growth, which was used to perform urban modeling and projection.The BA not only demonstrated the ability to find CA transformation rules in simulating urban growth, but also expressed the ability of each factor to explain urban growth.This suggested that the new BA-POO-CA model is effective in capturing the relationship between spatial factors and urban growth.
4.3 Suggestions of urban sustainable development
Cities in arid areas have unique urban patterns and urban growth patterns because of the influences of topography and environment (Wei et al., 2022; Zhang et al., 2023b).During the period of 2000-2020, urban growth in Urumqi City mainly concentrated in Xinshi District,Tianshan District, Saybagh District, and the surrounding low-lying areas, showing a distinct pattern of agglomeration (Fig.4d).Most of these areas are located in exceptional and extreme drought areas (Fig.1b).This may be related to the topography of Urumqi City, which is surrounded by mountains on three sides, forming a gourd-shaped valley basin that is wide from north to south and narrow from east to west, with mountainous areas accounting for more than 50.00% of the total area.The geographic location and topography of Urumqi City make its urban land use extremely limited (Mamitimin et al., 2023).In addition, the city is far from ocean,making it difficult for humid air to reach the western interior, and the scarcity of vegetation leads to high evaporation, low rainfall, and an arid climate with a threatened ecosystem and a very low carrying capacity of population (Mamattursun et al., 2022).This suggests that drought could have an impact on urban growth patterns, while the unplanned urban growth could exacerbate the further deterioration of drought.The combined effects of topography, climate, and human activities have limited the urban development of Urumqi City.
Therefore, the implementation of appropriate urban planning measures is important for the sustainable development of Urumqi City.According to the results, we proposed several measures of urban planning and municipal management for Urumqi City.First, drought intensity monitoring should be strengthened to explore the dynamic change mechanism of urban growth in arid areas, thus providing reliable data support for the sustainable development of cities in arid areas.Second, it is recommended that local governments should formulate rational urban planning policies and accelerate the construction of ecological cities (Hurlimann et al., 2021;Kandt and Batty, 2021).Third, given the constraints of natural environmental conditions, the advantages of structural links between cities within urban agglomeration should be utilized (Yu et al., 2019; Shen et al., 2022).
4.4 Applications of simulation results
Different models perform differently in the same region, and the same model performs differently in different regions (Gao et al., 2023).Asif et al.(2023) used CA-Markov model to study land use and land cover changes for Cholistan and Thal deserts in Punjab Province, Pakistan, with an overall accuracy of more than 87.00%.Liu et al.(2021) developed a CA model using Long Short-Term Memory Network to simulate urban pattern for Lanzhou City in semi-arid areas, and the overall accuracy of this model was 91.01%.Our BA-POO-CA model yielded an overall accuracy of 97.70%, demonstrating the validity of this model in arid areas.
Cities in arid areas must adapt to climate change and proactively address the consequences of extreme weather events.Our simulation results have broad potential applications, such as assessing the environmental impacts of urbanization and extreme weather events.For instance,our findings can aid in forecasting the environmental repercussions of urban expansion, thereby assisting urban planners in crafting sustainable urban development strategies, such as mitigating urban heat island effects (Cai et al., 2023; Han et al., 2023a, b).Simulating land use patterns across various scenarios enables the evaluation of impacts of urban growth on ecosystems, water resources, and air quality, providing a scientific foundation for policymakers' decisions.Moreover,given the climatic challenges of cities in arid areas, particularly in relation to extreme weather phenomena like heatwaves, droughts, and floods, modeling and projecting urban growth under targeted scenarios can facilitate early warnings, impact assessments, and the implementation of measures to mitigate disaster risks (Yu et al., 2023; Zhang et al., 2023a).Such proactive approaches can furnish policymakers with a scientific basis to refine urban planning and management, as well as enhance society's adaptive and resilient capabilities.
5 Conclusions
Modeling and analyzing urban growth in arid areas is crucial for sustainable development.We took into account the characteristics of cities in arid areas, selected drought intensity as a key factor, and developed a new CA model (BA-POO-CA model) using a heuristic algorithm to simulate and project urban growth in such areas.We calibrated the BA-POO-CA model using the 2000 and 2010 datasets of study area, validated the model using the 2010 and 2020 datasets, and finally projected its urban growth scenario in 2030.The results showed that the urban growth of Urumqi City over the past two decades mainly occurred in Xinshi District, Tianshan District,Saybagh District, and the surrounding low-lying areas, with a more pronounced agglomeration pattern.The evaluation results showed that BA-POO-CA model yielded an overall accuracy of 97.70% and FOMs of 35.50% in 2010, and 97.70% and 26.70% in 2020, respectively, indicating its effectiveness for cities located in arid areas.The inclusion of drought intensity has improved the performance of BA-POO-CA model in terms of FOMs, with increases of 5.50% in 2010 and 7.90% in 2020.This suggested that the urban growth of Urumqi City was affected by drought,and therefore taking drought intensity factor into account would contribute to simulation accuracy.Using exceptional and extreme drought area as a spatial constraint, we projected a possible scenario for Urumqi City in 2030 to help adjust urban planning and development policies.
Our model is readily applicable for simulating urban growth and future scenarios in global arid areas such as Northwest China and Africa.Despite the fact that our model is specific to arid areas,it is also applicable to coastal areas after adopting appropriate factors.Future work should focus on the following directions: (1) extending the basic theory of CA modeling for large-scale urban simulation in arid areas; and (2) incorporating representative meteorological and ecological factors to improve the projection capability of CA model for urban growth in arid areas.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This study was supported the National Natural Science Foundation of China (42071371) and the National Key R&D Program of China (2018YFB0505400).We thank the editors and anonymous reviewers for their useful suggestions on improving the quality of this article.
Author contributions
Conceptualization: TANG Xiaoyan, FENG Yongjiu; Data curation: TANG Xiaoyan, LEI Zhenkun, CHEN Shurui,WANG Jiafeng; Methodology: TANG Xiaoyan, LEI Zhenkun; Formal analysis: TANG Xiaoyan, CHEN Shurui,WANG Rong, TANG Panli, WANG Mian; Writing - original draft: TANG Xiaoyan; Supervision: FENG Yongjiu,JIN Yanmin, TONG Xiaohua; Writing - review and editing: FENG Yongjiu; Funding acquisition: FENG Yongjiu;Visualization: WANG Jiafeng, WANG Rong.All authors approved the manuscript.
杂志排行
Journal of Arid Land的其它文章
- Three-dimensional (3D) parametric measurements of individual gravels in the Gobi region using point cloud technique
- Spatiotemporal characteristics of seed rain and soil seed bank of artificial Caragana korshinskii Kom.forest in the Tengger Desert, China
- Afforestation with an age-sequence of Mongolian pine plantation promotes soil microbial residue accumulation in the Horqin Sandy Land, China
- Spatiotemporal variability of rain-on-snow events in the arid region of Northwest China
- Effect of coir geotextile and geocell on ephemeral gully erosion in the Mollisol region of Northeast China
- Assessment of runoff changes in the sub-basin of the upper reaches of the Yangtze River basin, China based on multiple methods
