基于姿态信息的双足移动机器人越障步态控制
2024-04-22刘晓铭华定忠黄国方钟亮民
刘晓铭,华定忠,张 静,黄国方,钟亮民
(1.南瑞集团(国网电力科学研究院)有限公司,江苏 南京 211106;2.国电南瑞科技股份有限公司,江苏 南京 211106)
0 引言
双足移动机器人是一种涵盖多个自由度与非线性约束的繁杂系统[1-2],控制双足机器人躲避或者跨越障碍物为一项极具挑战性的任务。其核心难点在于,双足机器人跨越障碍物时,双足重心大幅度向前倾斜,令其得到更多的跨越空间[3],但这与维持机器人稳定的约束条件相悖,且机器人上半身平衡能力较差,导致机器人更容易失稳跌倒。
面向越障步态控制问题,学者们从不同层面给出以下处理方案:吴晓光等[4]探究了双足机器人动力学模型,创建不同的空间操作环境,使用深度强化学习策略让双足机器人完成稳定行走目标;周江琛等[5]推算同一行走周期下,机器人步长变化的能耗最小质心高度,组建质心状态方程,以零力矩点稳定裕度约束为前提,构建二次约束规划模型,获得当前最优行走轨迹,完成步态控制。
但上述方法在机器人运行数量较多时,均不同程度地存在躲避或者跨越障碍延迟问题,在现实应用中无法满足实际需求。为此,本文提出一种基于姿态信息的双足移动机器人越障步态控制方法。
1 双足移动机器人动力学模型
为更好地实现稳定精准机器人越障步态控制,明确其运动规律是极为关键的步骤。假设双足机器人髋关节质量是A,2条腿质量都是a,腿部总长度是l,b是质心和髋关节的间距,c是质心和踝关节的间距,B是半圆弧足和踝关节的间距,d是半圆弧足半径。在机器人踝关节中引入脉冲动力,将其拟作机器人的能量推动力[6],机器人模型行走时分为双腿摆动与地面碰撞2个阶段。
a.双腿摆动阶段,设定δ为支撑腿和地面法线的夹角,φ为摆动腿和支撑腿夹角。按照能量守恒定律,使用拉格朗日方程创建双腿摆动方程,记为
[Al2+a(c2+l2+b2-albcosφ)]δ+[albcosφ-ab2]φ+(2albδφ-albφ2)sinφ-
(A+a)lsinδ-absin(φ-δ)=0
(1)
b.地面碰撞阶段,如果摆动腿在支撑腿前方,并贴合如式(2)的几何条件,则机器人的脚会和地面产生冲击力。
φ(ε)=2δ(ε)
(2)
式中:ε为腿部从摆动至产生冲击的耗时,也就是行走周期。
凭借踝关节推力瞬时作用特征[7],可近似获得机器人合力方向夹角,即
(3)
式中:E为反向作用力;e为踝关节摩擦力。
可将冲击前后机器人关节角速率之间的关系表示为:
F+(β)=F-(β)+V
(4)
(5)
F+=
(6)
(7)
式中:上角标“+”为冲击后;上角标“-”为冲击前;β为产生冲击时2条腿之间的夹角;V为机器人行走的平均速率;Q为踝关节弧足脉冲力与摩擦力的合力;L1为合力Q和髋关节之间的跨度距离;L2为合力Q和撞击点之间的跨度距离。
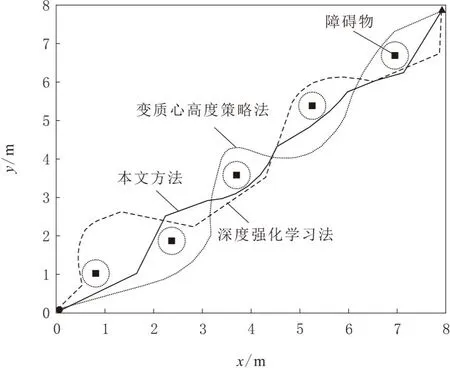
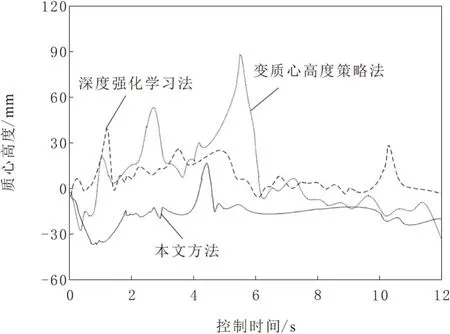
若A Alδ+=Alδ-cosβ+Qsinβ (8) φ+=δ+(1-cosβ) (9) 为提升双足移动机器人智能化程度,在越障步态控制中引入姿态信息,更准确地掌握机器人的运行姿态,完成精准越障。将双足移动机器人分成躯体、头部、左上肢、右上肢、左下肢和右下肢6部分。创建机器人部件检测器,其目标是利用该检测器,在图片中找出机器人对应部件方位[8]。以躯体部分为例,依照如下过程创建机器人部件检测器。 a.在已拍摄完毕的训练图片中裁剪躯体部位,将其旋转到竖直状态,采集一些机器人躯体的图片作为负例样本。 b.计算各样本图片的方向梯度直方图特征,取得1个矢量Z,矢量Z加上正例或负例标签,就表示相对的样本图片。 c.把获得的矢量引入AdaBoost算法内训练获得强分类器,记为 (10) 式中:S(·)为sigmoid函数;hi(·)为第i个矩形框长度计算函数。 关联性是获得机器人姿态信息的关键指标,以左上肢和躯体之间的距离关系为例,设定躯体方位是已知的[9],仅需计算左上肢当前处在何种方位即可。设定左上肢和躯干相连的边是g,二者在躯体的顶点k处相互连接,则边g的中心点和躯体顶点k之间的距离为 (11) 式中:xg、yg为边g的横纵坐标;xk、yk为顶点k的横纵坐标。 关联性评价指标最终表达式为 od=p(-1×(d-n))/(N-n) (12) 式中:p为关联常数;n为全部候选区域内的最小d值;N为全部候选区域内的最大d值。 可以看出,d值越小,关联度od的值越大,机器人姿态信息的关联程度越高。 骨骼密度能展现机器人每个部位的位置与走向,在人机交互中为一个核心识别特征[10]。通过获取骨骼数据系统评估机器人姿态,将候选区域的骨骼密度计算公式描述为 qj=r1q1+r2q2 (13) 式中:q1为骨骼点数量;q2为骨骼点居中水平;r1、r2均为计算权重,二者相加之和等于1。 得到足够的姿态信息后,为进一步优化越障步态控制精度,实现期望越障成效,设计一种基于神经网络前馈补偿[11]的机器人越障步态控制策略,神经网络训练数据为机器人姿态信息与障碍物图像信息。 利用摄像头获取障碍物图像信息[12],图像信息使用坐标系描述,将障碍物投影方位表示为 (14) 式中:u、w为横向与纵向参照点方位。 双足移动机器人越障时,使用具备前馈补偿性能的神经网络进行步态控制,针对机器人导线弯曲引发的不良影响创建前馈控制模型,在偏差与控制量之间组建补偿模型[13]。 神经网络前馈补偿控制器和神经网络分辨器的网络架构完全相等,都涵盖输入层、隐含层与输出层,不同之处是输入、输出2个层级的引入参数。以神经网络分辨器为例,详细分析双足移动机器人越障步态控制全过程。 设定I(1)、O(1)分别是神经网络第1层输入值与输出值,在输入层中,把机器人加速度传感器测量信号f与感知的姿态信息拟作输入量,并代入网络控制器输入端,同时将其输出值fi传递至网络的下一层,此时存在如下对应关系,即 O(1)=I(1)=f (15) 在隐含层内部,使用sigmoid函数[14]获得各节点输入的激励函数为 (16) 式中:si为第i个节点下的函数权重值。 输出层中,线性化计算隐含层获得的信息,把计算结果拟作权重,得到 (17) 式中:R为训练总次数。 梯度下降算法计算简便、及时性强[15],在神经网络参数学习中使用梯度下降完成运算任务。首先设置目标函数F(x)的值域,记作 (18) 式中:z为控制系统输出控制量;zn为神经网络分辨器补偿量。 神经网络学习的根本目的是让目标函数值为最小[16],设定控制周期的补偿量为tc,越障步态控制器的输出为to。控制系统的当前控制量t(j)为上述二者的总和,求出总和值即可完成神经网络训练,完成机器人智能化越障步态控制任务。 控制输出总和计算公式为 t(j)=tc(j)+to(j) (19) 式中:j为当前控制所需时间。 为验证本文所提方法能否完成精准的越障步态控制,对其进行实验分析,并把文献[4]深度强化学习法与文献[5]变质心高度策略法拟作对比组,实验软件为MATLAB。以某型号双足移动机器人为例,设置障碍物数量为5个,起点坐标是(0,0),目标点所处坐标是(8,8)。3种方法越障步态控制结果如图1所示,图中圆形为出发点,三角形为目标点,实心方块是障碍物,虚线部分为障碍物影响范围。 图1 3种方法越障步态控制结果对比 由图1可知,本文方法的越障路径较为平滑,能以最快速度完成越障,越障路径最为合理,有效改进了机器人在障碍物停滞不前的现象,越障性能显著优于其他2种方法。 通过越障步态控制偏差、质心高度和SI指数来验证方法稳定性。越障步态控制偏差实验中,设定实验时间为5 min,越障路径总长为2 000 m,且有500 m路径处于崎岖地段,障碍物影响范围较大,分析3种方法下机器人在二维平面垂直和水平方向上的越障姿态偏差,结果如图2所示。 图2 不同轴位的越障步态控制偏差对比 由图2可知,越障控制下0~80 s与130~300 s时,机器人控制偏差浮动较小,偏差控制状态较好,而在90~120 s时发生较大浮动。这是由于机器人经过了崎岖地段,越障时会产生一定摆动。但和其他2种方法相比,本文方法利用姿态信息感知功能,快速调整了机器人重心,增强机器人在垂直及水平方向的越障水准,证明了本文方法在极端情况下也能进行更细微的行走操作,实现可靠的越障任务。 双足移动机器人的初始质心高度采用倾斜平台法测得,以初始质心高度为中心零点,当双足移动机器人跨越障碍运动时,其质心的高度会发生变化,当运动质心高于初始质心则为正数;当运动质心低于初始质心则为负数。假设机器人在平地运动,路面上安置一个高度为7 m的障碍物,观察双足机器人越障时的质心波动,结果如图3所示。由图3可知,面对7 m高的障碍物,本文方法下机器人成功越障后,质心高度波动情况明显小于深度强化学习法和变质心高度策略法,证明了本文方法可以花费较小的动力就能越过障碍,垂直方向能量耗损有较大改善,完成了越障步态控制的预期目标。 图3 机器人越障质心浮动对比 采用稳定性指数(stability index,SI)衡量机器人越障步态控制水准,该指标计算公式为 (20) 式中:λt为实测零力矩点;λs为预期零力矩点;λmax、λmin分别为零力矩点的最大值与最小值。 设定越障路径总长为100 m,在行走第9 s引入一定外力扰动,SI指数变化趋势如图4所示。 图4 SI指数变化趋势 由图4可知,本文方法双足机器人行走受到扰动时,步态控制的SI指数波动较小,具备更好的抗干扰性能,动态稳定性也随之提高,综合性能优于其他2种方法,在真实场景应用中可获得更优的实践结果。 为有效处理双足移动机器人越障波动性大、稳定性不高的实际问题,结合人机交互概念,本文提出一种基于姿态信息的双足移动机器人越障步态控制方法。分析机器人动力学特征并划分姿态规律,使用拥有前馈补偿性质的神经网络进行越障步态控制训练。实验过程中,利用不同指标和传统算法进行对比,充分验证了所提方法在越障步态控制方面的实用性与可靠性,为提升机器人整体越障性能打下坚实基础。2 双足移动机器人越障步态控制
2.1 姿态信息获取
2.2 越障步态控制
3 实验分析

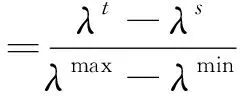

4 结束语
