典型变电站沟内线缆HEMP耦合仿真研究
2024-04-22龚渝涵李俊娜田君杨黄齐翔巫方正李世纪王皓琰
龚渝涵,李俊娜,田君杨,黄齐翔,巫方正,李世纪,王皓琰
(1.西安交通大学电气工程学院,陕西西安 710049;2.广西电网有限责任公司电力调度中心,广西南宁 530021)
0 引言
随着对电网依赖程度的提高,高空电磁脉冲(High-altitude Electromagnetic Pulse,HEMP)对电力系统的影响日益受到关注。高空爆炸产生的电磁脉冲覆盖面积可达数千公里,同时覆盖范围内的电子设施将受到影响而无法运行,通信系统被中断,这是由于HEMP 的早期阶段具有前沿快、场强高以及高频分量丰富等特点,可以耦合到暴露在外部的线缆上或设备孔缝中,感应出幅值较高的感应电压或电流,并通过传导进入电力设备内部,进而对电力系统造成重大威胁[1-5]。几十年来,国内外在对电力系统中HEMP 的响应研究中,在电力系统中长度可达数千公里的架空输电线路的计算或试验中将辐射环境转化为传导环境已经得到了很好的研究[6-12]。然而,由于各个变电站的内部配置细节不尽相同,对于电力系统中变电站内部线缆和设备的HEMP 耦合研究相对较少。
与直接暴露在空气中、高度可达数十米的架空输电线路不同[13-14],随着变电站智能化程度增加,配电、测量和开关设备等越来越多的电子设备的集成度和精度都在增加[10-19],且都包含在主控室中,而站内户外线缆绝大部分分布在深度1 m 左右的地下电缆沟内,被含有钢筋的混凝土盖板覆盖,并不直接暴露在辐射环境中。站内线缆通常是具有屏蔽和金属铠装的多芯线缆,复杂的内部结构使其区别于输电线路。综上所述,输电线路的HEMP 耦合计算或试验结果并不能代表站内控制线缆的耦合响应水平,且使用单一的传输线方程对变电站整体环境进行分析计算非常困难,而相比三维有限元方法,利用三维的传输线矩阵(Transmission Line Matrix,TLM)法在仿真电磁波相关领域能够更高效地获得可靠的分析结果[20]。
因此,本文基于典型变电站的现场布局,利用TLM 算法对其电缆沟内线缆的HEMP 耦合水平进行研究分析,研究结果对变电站内部的线缆以及相应连接设备的HEMP 防护措施选择具有一定的参考意义。
1 HEMP的早期环境及仿真算法
1.1 HEMP早期阶段的频域和时域波形
根据IEC 标准[21-22],早期阶段的时域波形表达式如式(1)所示:
时域波形如图1(a)所示。脉冲波形10%~90%的上升时间大约为2.5 ns,从峰值到50%幅值处的下降时间大约为19 ns。

图1 HEMP早期阶段的时域和频域波形Fig.1 Time-domain and frequency-domain waveforms of HEMP early stage
式(1)通过傅里叶变换可以得到对应的频谱表达式(2)[21]:
式中:E(ω)为电场的频域表达;ω为频率f对应的角频率,ω=2πf;t为脉冲持续时间。
式(2)中ω=2πf,对应频域波形如图1(b)所示。
1.2 仿真算法
HEMP 早期波形前沿仅有2 ns 左右,持续时间短,需要对线缆耦合水平进行时域分析,因此本文拟定三维TLM 方法对线缆耦合进行时域研究分析。由于TLM 算法的建模空间有限,模型的边界反射会造成入射波在线缆所在位置产生叠加,使得最终结果产生误差。因此在模型构建中,通过对边界条件的设置减弱边界反射带来的影响,将地面侧边界设置为电边界(Et=0),其余边界条件设置为开放边界(open),频率计算上限取250 MHz。
为验证模型边界反射的可靠性,利用传输线方程和时域有限积分(Finite Integral Method,FIT)法对仿真算法进行对比分析。图2 为平面波辐照下传输线耦合模型。线缆长度为L,距离地面高度为h,线缆两端接入电阻分别为R1和R2。高空爆炸产生的HEMP 辐照到线缆上时可以近似视作平面波,平面波被分解为入射电场量和磁场量,入射角ψ为传播方向与地面的夹角,方位角ϕ为传播方向在地面的投影与线缆所在方向的夹角为波的传播方向,α为极化角。

图2 平面波辐照下单导体传输线模型Fig.2 Model of single-conductor transmission line under plane wave irradiation
采用全电压公式求解传输线方程时,有损地面上的负载电流和电压可以表示为对传输线上分布源的积分形式,得到下列负载电流和电压的方程,即:
式中:Zc为线缆的特征阻抗;ρ1和ρ2为两端负载反射系数;γ为传输线上单位长度传播常数;S1和S2为源矢量;I(0),I(L),V(0),V(L)分别为线缆首、末端响应电流和电压。
γ可由式(5)给出:
式中:Z,Y′为传输线单位长度参数;Zw为导体内阻抗;为考虑地面散射磁通等效成的大地单位长度阻抗;为对应的大地单位长度导纳;C′,L′为传输线的分布参数。
式中:σg和εg为大地参量;γg为电磁波在大地中的传播常数。
式(3)和式(4)中的源矢量S1和S2可表示为:
当地面是有损电导体时,电磁场可以穿透地面,且随着大地深度以指数规律衰减,分布式电流源和分布式电压源如式(8)所示:
将式(5)—式(8)代入式(3)和式(4)就可以解出有损地面上传输线两端的负载上的电压、电流响应的频域解。将频域解经过傅里叶逆变换可以得到时域解。
以α=0°,ψ=90°的平面波为激励,线缆为长度L=10 m,半径a=1 mm 的导线为计算实例。距离地面高度h=10 cm,地面电导率σ=0.01 S/m,相对介电常数εr=10。分别比较3 种计算方法下不同入射角的线缆末端开路电压水平以验证三维电磁仿真软件中边界条件设置以及计算的可靠程度。
从图3 的波形对比可以看出,TLM 算法与FIT算法和传输线理论吻合得较好,等效性得到验证,可以利用优化边界后的TLM 方法对变电站整体耦合进行仿真分析。
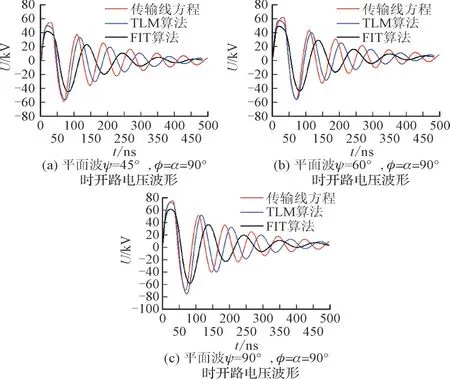
图3 3种计算方法负载响应结果对比Fig.3 Comparison of load response results with three calculation methods
2 典型变电站及内部线缆模型简化
2.1 变电站中典型电缆沟结构
从主控室到变电站内最长的沟槽中电缆以及相应的电缆沟布置作为站内耦合HEMP 威胁最大的途径被重点研究。简化后的变电站平面示意图如图4 所示,其中地面的电导率σ=0.01 S/m,相对介电常数εr=10,μr=1。

图4 某典型变电站主要设施及电缆沟最长段布局Fig.4 Layout of main facilities and the longest section of the cable trench of a typical substation
2.2 场站内电缆沟及端子箱内部细节
图5 展示了某典型变电站场的电缆沟的细节。电缆通常敷设在沟的中下部分,沟底是大约0.2~0.3 m 厚的淤泥。电缆沟内部存在接地排,通常在沟的终端与接地网或接地棒相连接。

图5 电缆沟及端子箱的内部结构Fig.5 Internal structures of cable trench and terminal box
若针对所有内部细节进行建模,会产生大量的网格从而拖慢计算速度,因此计及最恶劣情况对模型进行化简。首先,只考虑1 根信号线、控制线或电源线布设的情况,而所有其他导线和电缆都已拆除;其次,将接地排和支架简化成整根的接地导体且位于导线正下方;最后,除了电缆沟盖板外,不考虑站内的其他水泥结构,将其视作电导率均匀且相同的大地结构。
参考实际情况搭建了电缆沟及其内部线缆的简化模型如图6,以黑色粗实线代指其中的线缆。其中电缆沟盖板长W=80 cm,内部增加强度的钢筋半径R=0.5 cm,电缆沟深度D=90 cm,电缆沟底的宽度w=80 cm,接地排距离盖板下表面的深度d=50 cm。
2.3 线缆型号参数
根据典型变电站的调研结果,本研究采用站内使用频率最高的屏蔽控制电缆KVVP2-22-4×4 进行仿真分析,其横截面和对应的相关参数如图7 所示。其中芯线半径rwire=1.12 mm,屏蔽层半径Rshield=4.7 mm,厚度为0.05 mm,铠装层半径Rarmor=6.6 mm,厚度为0.4 mm,线缆整体半径Rwire=8.5 mm。4 根芯线中常有2 根用作备用,正常工作状态下处于置空状态。
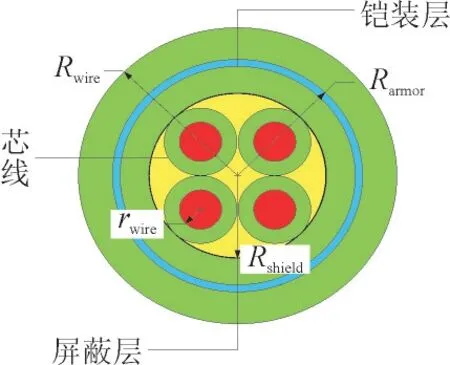
图7 KVVP2-22-4×4型号线缆截面图Fig.7 Cross-section diagram of KVVP2-22-4×4 cable
3 典型变电站电缆沟内部线缆响应水平仿真
参考某典型变电站的实际调研结果中各种线缆的两端接线形式,通过仿真计算二次回路中具有代表性的3 种线缆[23-30]在电缆沟内的耦合水平:两端开路线缆、传输模拟量线缆及传输开关量线缆。
考虑到站内大体积的金属设备如变压器、PT/CT 等设备对HEMP 的反射造成沟内线缆耦合的影响,对平面波不同的入射角、极化角分别进行仿真分析,以探究变电站电缆沟内线缆的最大耦合水平。电场强度作为直接输入量,可以对端口耦合水平进行初步估计。在保持ψ=ϕ=90°不变时,对不同极化角α情况下的HEMP 入射平面波进行分析,此时线缆端口附近的电场强度如下图8 所示。
由图8 可以看出,主控室侧的电场强度大于户外端子箱侧,对应线缆端口平均耦合水平应高于户外端子箱侧。在改变极化角的情况下,户外端子箱侧的电场强度在α=30°时达到最高,主控室侧的电场强度最高在α=60°时产生,意味着两端的响应水平分别在α=30°和α=60°时达到最高。
3.1 屏蔽层开路线缆
站内二次系统中屏蔽层开路线缆两端均接模拟量采集模块,输入阻抗在兆欧级别,同时芯线和屏蔽层、铠装层之间的等效阻抗也达到百兆欧。为防止屏蔽层接地时,电磁干扰在屏蔽层上产生干扰信号或者大电流对芯线上传递的信号造成干扰或者终端设备造成损伤,屏蔽层始终处于开路状态,以兆欧级别的接地电阻进行等效。
当铠装层、屏蔽层和芯线都处于等效开路的状态时,电荷没有泄放通道,而直接表现为电压形式体现在末端响应水平上。保护ψ=ϕ=90°时,极化角α从0°到90°时线缆两端最大耦合响应水平如图9 所示,线缆两端最大耦合响应水平发生在α=60°的情况下,此时主控室内设备侧末端感应电压峰值约为33 kV,户外端子箱侧末端感应电压峰值能够约为49 kV,可能会对设备外壳进行放电导致损伤。
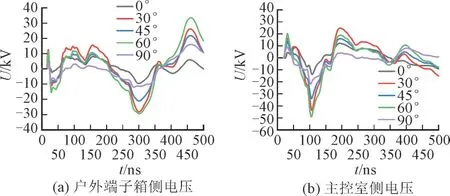
图9 改变α 时平面波辐照两端开路线缆耦合水平变化Fig.9 Changes in coupling level of open cables at both ends of plane wave irradiation when α is changed
图9 中线缆两端波形并不相同,因为线缆在电缆沟内会产生方向不同的多段耦合,此时电压电流在传输过程的衰减和端点处不完全相同的电磁环境使得两个端点处的耦合响应水平有较大差距。且线缆末端的耦合响应波形在大约400 ns 时存在明显的反射,这是线缆另一端的响应波形通过介质传播来到测量端。这也导致仿真结论与电场分析的户外侧在α=30°达到最大不同,主控室侧的反射的波形到达端子箱侧,使得最大值同样发生在α=60°。
3.2 传输开关量的线缆
连接室内柜体及端子箱的信号线,将二次设备的开关状态量传递回主控室进行监测,同时主控室可以通过改变开关量对二次设备进行动作控制。
这段线缆两端均接入开关量采集模块,输入阻抗在兆欧级别。由于开关量传输的信号水平较低,易受到电磁干扰使得测量数据不准确,因此屏蔽层需要两端接地以保护信号传输不受干扰。假设土壤的接地阻抗为1 Ω。
传输开关量的线缆的主要接线特征在于屏蔽层双端接地,图10 为ψ=ϕ=90°保持不变,改变α时的屏蔽层响应电流变化。
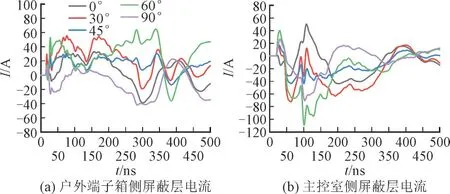
图10 改变α 时的屏蔽层电流波形Fig.10 Shield current waveform when α is changed
此时开关量传输线缆的响应水平在α=60°达到最大,屏蔽层感应电流最大能够达到110 A 左右。
ψ=ϕ=90°,α=60°时铠装层和芯线的响应水平如图11 所示,此时铠装层电压的峰值大约为1.2 kV,芯线上的感应电流峰值仅在0.23 mA 左右。
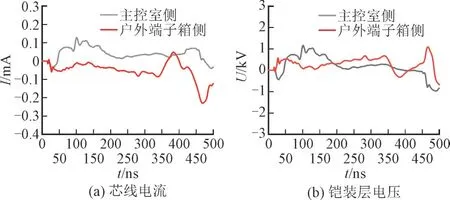
图11 α=60°时的线缆末端响应水平Fig.11 Response level of cable terminals at α=60°
开关量传输线缆屏蔽层的大电流可能会在端子箱内产生时变的电磁场,导致线缆内部传输信号被干扰,导致智能设备动作。
3.3 传输模拟量的线缆
连接端子箱及室内柜体的信号线,将从设备上采集到的模拟量传输回主控室,便于工作人员的控制和监测。这段线缆,两端均接入模拟量采集模块,输入阻抗在兆欧级别,铠装层开路。和开关量类似,模拟量的信号水平也较低,因此屏蔽层需要两端接地,但模拟量为连续信号,需要在线缆的前端(户外端子箱侧)有一根芯线单端接地,使信号传输形成回路。假定土壤的接地阻抗为1 Ω。
由于模拟量线缆的屏蔽层和一根芯线接地,导致二者上流过的感应电流变大。此时屏蔽层和接地芯线上的感应电流波形随极化角α改变时的波形如图12 所示。
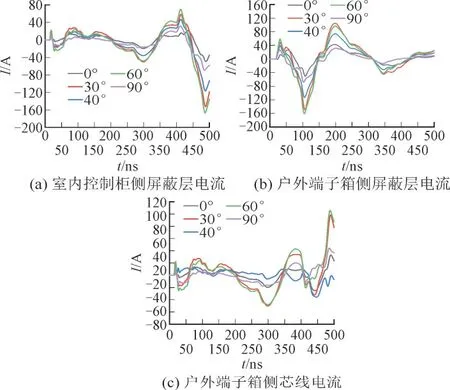
图12 改变α 时平面波辐照模拟量线缆两端耦合水平变化Fig.12 Coupling level variation at both ends of plane wave irradiation analog cable while changing α
在ψ=ϕ=90°保持不变的情况下,当极化角α=60°时末端感应水平达到最大值,此时接地芯线和屏蔽层的感应电流达到了100 A 以上,可能会直接损毁末端的智能监测设备。
屏蔽层双端接地使得铠装层和芯线上的耦合响应水平有很大的改善。芯线上耦合到的干扰信号被屏蔽层所保护,除接地芯线,其他感应电流如图13 所示,峰值均不超过7 mA。
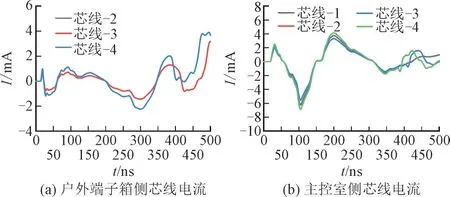
图13 ψ=ϕ=90°,α=60°时其他芯线上的电流Fig.13 Current on other cores at ψ=ϕ=90°and α=60°
4 现场试验与仿真计算的对比验证
搭建了高度H=8 m,半锥角θ=40°的双锥转线栅天线进行现场试验。此天线能够产生满足IEC 标准的水平极化双指数辐射波形,当脉冲源所加载得激励水平为420 kV 时,距离地面3 m 高度处的电场波形如图14 所示,上升时间约为2.01 ns,半高宽约为19.04 ns,电场幅值约为56.3 kV/m。
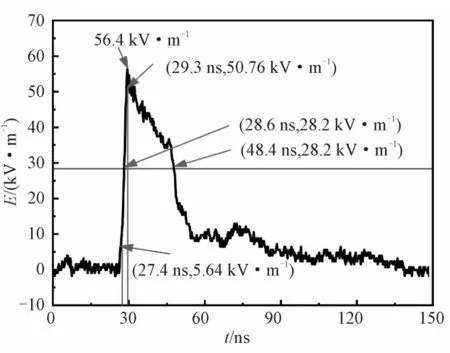
图14 脉冲源正下方3 m处水平电场强度波形Fig.14 Waveform of horizontal electric field strength at 3 m directly below the pulse source
以开关量传输线缆为例设置现场试验,线缆屏蔽层两端接地,其余开路,线缆型号参考图7,长度为8 m,距离地面高度0.6 m。仿真模型参考现场试验设置1:1 搭建,现场布设如图15 所示。

图15 现场试验布局Fig.15 Field test layout
试验与仿真所得到的屏蔽层短路电流波形如图16 所示。仿真和试验所得短路电流的峰值均为70 A 左右,波形趋势基本一致,可以验证第3 节中典型变电站线缆HEMP 耦合计算结果的准确性。
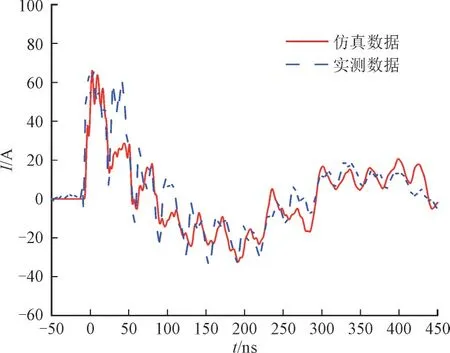
图16 仿真与实测数据的波形对比Fig.16 Comparison of simulated and measured waveform
5 结论
本文通过对比传输线方程、FIT 方法以及TLM算法的等效性,采用TLM 方法对典型变电站线缆的不同连接方式、平面波入射时的不同极化角进行了仿真分析,最后通过现场试验对仿真算法进行了最终的验证。文章最终得到以下结论:
1)改进边界条件后的三维TLM 算法的无限大地面模型可与传输线方程和FIT 算法等效。
2)对于本文所研究的典型变电站,线缆末端的耦合响应水平在α=60°时达到最大。两端开路线缆末端的响应水平为高达49 kV 的电压量。传输模拟量的线缆的屏蔽层和接地芯线电流最高可以达到160 A。传输开关量的线缆屏蔽层电流约100 A,会在金属柜体的内部产生时变的电磁场,产生干扰信号。
3)现场试验和仿真计算结果在峰值和波形上都有较好的一致性,进一步验证了仿真的等效性。
