基于遗传算法小波神经网络的光伏电站发电量预测方法

2024-04-22张晓忠陈久益白建波黄悦婷汤霜霜

智慧电力 2024年4期

周强，张晓忠，陈久益，沈炜，白建波，黄悦婷，汤霜霜

（1.国家电投集团江苏新能源有限公司，江苏南京 210000；2.河海大学机电工程学院，江苏常州 213022）

0 引言

在当前全球环境持续恶化的形势下，对清洁可再生能源的需求变得更加迫切。光伏能源作为一种方便且高效的可再生能源获取方式，得到了快速发展并受到广泛关注。随着“碳中和”[1]成为中国可持续发展的战略目标，以及光伏技术的不断成熟，中国的光伏产业也在全面推进。光伏电站是光伏发电系统的核心，其发电量的精确预测对电力系统的稳定运行和能源管理极为关键[2-3]。随着光伏电站规模的扩大和技术的进步，精确预测光伏电站发电量已成为行业发展的重要课题。光伏电站发电量预测在提升电站控制和调度效率、确保电网安全稳定运行方面扮演着重要角色。目前，预测方法主要分为物理法和数学统计法2 大类。物理法通过预测太阳辐照量，再结合光电转换效率公式来推算发电功率[4-5]。数学统计法则是直接利用电站历史数据来预测发电功率。而随着机器学习技术的进步[6]，采用遗传算法小波神经网络（Genetic Algorithm Wavelet Neural network，GA-WNN）进行发电量预测的方法正日益受到重视，成为一种新兴的预测技术。

目前，已有不少针对GA-WNN 进行发电量预测的研究成果。文献[7]通过建立1 种反向传播（Back Propagation，BP）神经网络对气象数据进行分析，实现对光伏电站发电量的预测，结果表明采用传统的BP 神经网络所得到的数据精度不够准确。文献[8-9]采用改进的长短期记忆（Long Short-Term Memory，LSTM）神经网络对发电功率进行预测，结果表明在给定因素条件下预测精度较准确，但在复杂条件下的预测精度仍存在一些误差。文献[10]采用基于人工鱼群算法-反向传播（Artificial Fish Swarm Algorithm-BP）神经网络对光伏功率进行预测，其优点是输出功率精度高、训练耗时短，缺点是在预测结果的中段输出功率会出现较大的波动。文献[11]在混合小波神经网络（Wavelet Neural network，WNN）的基础上通过辐照度对发电量进行间接预测，结果表明WNN 较人工神经网络（Artificial Neural Network，ANN）的预测精度更好。文献[12-14]对基于粒子群优化算法（Particle Swarm Optimization，PSO）的BP 神经网络与基于遗传算法（Genetic Algorithm，GA）的BP 神经网络进行研究，并与传统的BP 网络进行对比，结果表明PSO-BP神经网络与GA-BP 神经网络的发电量预测精度都要高于传统网络，且PSO-BP 神经网络较GA-BP 神经网络而言计算精度更优。

综上所述，本文针对光伏电站发电量预测不准确及多种气象因素下预测结果出现波动的问题，提出1 种基于GA-WNN 的光伏电站发电量预测方法。该预测算法可以通过训练使所需参数得到自动调整，避免过拟合等问题，同时可通过利用遗传算法的全局搜索能力和小波分析的时频特性来提高光伏发电的预测精度。实例分析表明，该GA-WNN预测模型具有更小的误差和更高的预测精度，适用于精确预测光伏电站的发电量。

1 光伏电站发电量预测模型

1.1 影响因素

光伏电站发电量受多种气象因素影响，本文将太阳辐照强度、温度、风速和湿度作为主要影响因素[15]进行分析。

1）太阳辐照度。太阳辐照度受多种因素制约，如组件的地理位置、天气变化和辐照角等。长期监测发现，辐照度的变化具有周期性，并且与电站发电效率基本一致，二者呈正相关。研究显示，辐照度是影响光伏系统发电效率最关键的因素。

2）温度。当温度上升时，光伏组件上的电流增大，但同时电压变小，总体上功率变小。一般来说，温度的升高会引起晶体硅电池的输出电压的变化，当温度上升1℃时，晶体硅电池的输出电压大约下降0.5%左右[16]。

3）风速。风速大小会影响空气的流动速度，从而影响温度高低。当风速增大时，则光伏组件背板温度下降，使得组件的发电效率提高；相反地，若风速变小时，则光伏组件背板温度升高，使得组件的发电效率下降。

4）湿度。当空气相对湿度增大时光照受到影响，通过折射或衍射降低光线强度，从而影响辐照度的大小。同时，湿度的大小在一定程度上会影响环境温度，空气湿度的增加会使环境温度降低。长期监测发现，环境湿度与发电效率一定程度上呈现负相关关系。

1.2 数据预处理

为分析光伏电站发电量与以上4 种因素的相关性，本文采用CatBoost 权重计算方法，找出原始特征集合中不同相关程度的特征。数据集参数按其计算权重的排序结果选取，包括辐照度、环境温度、瞬时风速、空气湿度和发电功率，采用30 min 的采样周期来进行采样。为了保证预测的精度，采用最大最小归一化预处理的方式对实验预测数据进行筛选，将所有样本数据转化为0～1 之间的数[17]，所得数据均为无量纲。最大最小法数据预处理表达式为：

式中：xM为第M个样本数据；xmin为样本数据最小值；xmax为样本数据最大值。

1.3 预测模型建立

小波神经网络是以传统BP 神经网络[18-20]结构为架构，将小波基函数作为隐含层的传递函数所构建的神经网络。这些小波基函数用于对输入数据进行变换和非线性映射以提取时频特征，其拓扑结构如图1 所示。其中，l为输入层的节点总数，n为隐含层的节点总数，m为输出层的节点总数。Xl为输入层的输入数据，Wij为连接输入层第i个节点到隐含层第j节点的权重，Wjk为连接隐含层第j个节点到输出层第k个节点的权重，Ψn为母小波函数Ψ（x）通过伸缩和平移操作得到的隐含层全部节点小波基函数集合，Ym为输出层的输出数据。

图1 小波神经网络拓扑结构Fig.1 Wavelet neural network topology

将太阳辐照度、环境温度、瞬时风速和空气湿度的4 项实时数据作为输入数据输入，故输入层的节点数为4。输出数据仅为发电量1 项实时数据，则输出层的节点数为1。隐含层的节点数可根据式（2）计算所得，结合仿真实验可知隐含层最优节点数为8。基于GA-WNN 的光伏电站发电量预测模型为：

式中：a为[1，10]之间的任意常数。

2 GA-WNN预测

2.1 GA-WNN预测流程

GA-WNN 融合了神经网络和小波分析理论，在BP 神经网络的架构上以小波基函数为隐含层的传递函数构建神经网络。这种网络模式不仅具备小波变换和网络的优势，还具有时频局域化特性和自学习能力。在实际运行中，小波神经网络展现了较强的泛化能力和对数据及函数变化的自适应性，其预测精度相较于传统BP 神经网络更为准确。然而，小波神经网络在算法上采取最速下降法，与传统BP 神经网络存在相似问题，如可能陷入局部最优从而导致预测的精度出现偏差。为此，研究者引入遗传算法，该算法具有高鲁棒性和全局搜索能力，能有效提升网络模型的预测精度[21]。结合小波神经网络和遗传算法[22]，可更有效地应对复杂数据模式并提高预测性能。GA-WNN 预测流程如图2所示。

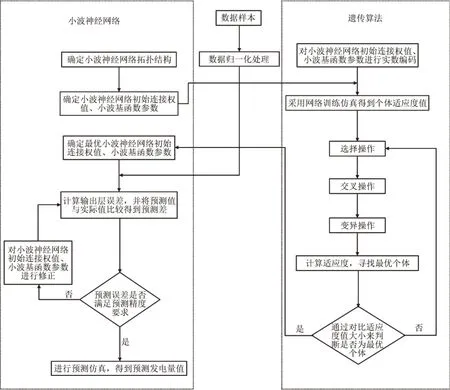
图2 GA-WNN预测流程Fig.2 GA-WNN prediction flowchart

2.2 遗传算法寻优

遗传算法[23-24]是1 种模仿自然选择过程的算法，其基本思想是通过不断的选择、交叉和变异操作，在1 个种群中搜索最优解。在这个算法中，个体的适应度是其在选择过程中生存和繁殖概率的决定因素，从而模拟了生物进化的基本原理。通过不断演化种群，遗传算法能够在大规模、复杂、非线性的问题空间中寻找全局最优解或近似最优解。遗传算法具体流程如下：

1）对小波神经网络初始连接权值、小波基函数参数进行实数编码。根据网络拓扑结构来计算参数的个数，以此来确定个体编码的长度，网络参数采用实数编码的方式组合而成实数串，将实数串视为遗传算法的个体，通过随机选取的方式构成初始种群。

2）采用网络训练仿真得到个体适应度值。将个体的网络参数导入网络中进行训练，通过模拟仿真来得到个体适应度值F，F值的大小反映了个体的适应能力的大小，其表达式为：

3）选择操作。根据适应度值，选择一些个体作为父代进行选择。一般来说适应度值高的个体选中的概率相对较高。个体选取概率表达式为：

式中：GK为第K个个体选取概率；FK为第K个个体的适应度值；N为种群个体总数。

4）交叉操作。通过模拟基因组合的方式，将父代的个体通过实数交叉法进行交叉得到子代，交叉概率一般取0.8。

5）变异操作。为了丰富种群的多样性，对于每个子代个体，通过引入随机概率生成新的个体。这种变异操作的变异概率通常设置为0.05。

6）计算适应度，寻找最优个体。通过计算适应度值F，来确定最优新个体。不满足条件的个体将进入迭代过程，迭代过程中会重复进行选择、交叉和变异操作，直至找到满足条件的个体。

在遗传算法流程中，通过将初始化的小波神经网络的连接权值和小波基函数的参数作为输入参数，经过遗传算法寻优，输出最优初始权值和参数，来构建优化的小波神经网络。

2.3 小波神经网络预测

将归一化预处理后的预测样本数据导入到小波神经网络中进行网络预测，具体流程如下：

1）确定小波神经网络拓扑结构。本文的小波神经网络的拓扑结构是以传统BP 网络的结构为基础，以小波基函数为隐含层的传递函数而构成的神经网络。

2）确定小波神经网络初始连接权值、小波基函数参数。初始化小波神经网络连接权值和小波基函数的伸缩因子和平移因子，将初始化的参数作为输入，导入到遗传算法中进行迭代。

3）确定最优小波神经网络初始连接权值、小波基函数参数。将遗传算法通过优化搜索得到的最优参数用于网络参数的初始化，包括初始连接权值和小波基函数参数等的赋值。构建GA-WNN 的数学模型为：

式中：Tj为隐含层第j个节点的输入值；aj为隐含层第j个节点的伸缩因子；bj为隐含层第j个节点的平移因子；σ（·）为输出层的激活函数；ψ（·）为Morlet 小波基函数；t为函数输入自变量；ψa,b（·）为包含伸缩因子a与平移因子b的传递函数表达式；yj为隐含层第j个节点的输入值。

4）计算输出层误差，并将预测值与实际值比较得到预测误差。通过将测试数据输入到网络中进行测试，将得到的预测输出值与数据的期望输出值进行对比分析，得到预测误差E为：

所得的预测误差与预测精度进行对比，若满足要求则开始预测仿真，若不满足要求则对小波神经网络初始连接权值、小波基函数参数进行修正，然后重新进行预测误差计算对比。

3 实例分析

以江苏地区夏秋季某电站发电量数据及气象数据为数据样本，分别对BP 神经网络、WNN，GABP 和GA-WNN 4 种预测模型进行仿真分析。对于晴天、雨天、阴天分别采用30 组数据作为训练集进行训练，以预测误差为基准来修正连接权值和小波函数的参数，不断对发电量进行预测测试，使得测试值逼近期待值。最后，将样本数据导入测试好的网络中，得到最终的预测值。

参考文献[25-26]对各类神经网络的参数进行选择，当预测模型的输入层节点数为4、输出层节点数为1 时，BP 神经网络和GA-BP 的隐含层节点数选9[27-28]，WNN 与GA-WNN 的节点数选8。设置遗传算法的种群规模为10，最大的迭代数为50，交叉概率与变异概率分别为0.2 和0.1，适应系数为1。经模型预测训练的期待值与预测值的对比可知，4个模型均为最优模型或近似最优模型。选取7—9月天气数据中较为典型的数据，得到晴天、阴天、雨天3 种天气类型下具体预测参数如表1 所示。

表1 天气类型预测参数Table 1 Weather type prediction parameters

3.1 晴天、阴天、雨天环境预测结果

本文通过发电效率的大小来反映发电量的大小。对比BP 神经网络、WNN，GA-BP 和GA-WNN4 种预测模型，得到晴天时各时刻发电功率与相对误差预测值曲线如图3 所示。

图3 晴天时各时刻发电功率与相对误差预测值曲线Fig.3 Prediction curve of power generation and relative error at different times in sunny days

由图3 可知，图3（a）中4 种模型的预测值与实际值的变化趋势一致，在13：00 左右出现下降趋势的原因是出现云层遮挡，故发电效率出现下降趋势。图3（b）中，GA-WNN 的相对误差最小，即反映发电功率实际值与预测值最为相近，其次是GA-BP的预测精度较高，传统的BP 神经网络的准确度较差。

阴天时各时刻发电功率与相对误差预测值曲线如图4 所示。由图4 可知，图4（a）中各模型的发电功率是波动上升的，到13：30 时分达到最高峰约为2 000 W，然后开始波动下降，最小值约为300 W，4 种模型的预测值的变化趋势，与实际值的变化趋势一致。图4（b）中，GA-WNN 的相对误差最小，预测的精度最好，结果优于其余3 种模型。

图4 阴天时各时刻发电功率与相对误差预测值曲线Fig.4 Prediction curve of power generation and relative error at different times in cloudy days

雨天时各时刻的发电功率与相对误差预测值曲线如图5 所示。

图5 雨天时各时刻发电功率与相对误差预测值曲线Fig.5 Prediction curve of power generation and relative error curve at different times in rainy days

由图5（a）可知，雨天的功率变化趋势较为复杂，且各模型与实际值的贴合程度不如前2 种天气环境。图5（b）中GA-WNN 的相对误差最小，其预测的准确度最好，较其他3 种模型而言，优势比较明显。

3.2 对比分析

由图3—图5 可知，BP 神经网络、WNN，GA-BP和GA-WNN 4 种模型所对应曲线依次更贴近实测曲线，初步判断4 种模型预测精度逐步提高。对比4 种模型所对应的相对误差可知GA-WNN 的相对误差最小。为进一步验证模型优劣，采用平均绝对误差（Mean Absolute Error，MAE）、平均绝对百分比误差（Mean Absolute Percent Error，MAPE）、均方根误差（Root Mean Square Error，RMSE）作为预测模型的性能指标，来反映预测值的精度，其物理量分别用EMA，EMAP，ERMS表示，表达式为：

4 种预测模型在3 种天气类型下的EMA，EMAP，ERMS预测对比如表2 所示。

表2 EMA，EMAP，ERMS预测对比Table 2 Prediction comparison of EMA，EMAP，ERMS

由表2 可知，在3 种不同天气条件下，通过比较4 种不同模型的预测性能指标，结果表明GA-WNN具有最高的预测精度。这一发现表明，利用小波分析作为神经网络的隐含层，并通过遗传算法来优化网络结构是有效的，能够在一定程度上解决局部最优问题，从而提升网络的预测能力。再次证明这种方法适用于光伏电站发电量的预测，可以增强预测的可信度。