一种提高数字控制LCL型并网逆变器对电网阻抗鲁棒性的补偿策略

2024-04-22金衍珍戴哲仁黄金平李昱泽

智慧电力 2024年4期

金衍珍，林丽，戴哲仁，朱淼，卞京，黄金平，李昱泽，4

（1.国网温州供电公司，浙江温州 325700；2.国网浙江省电力有限公司，浙江杭州 311500；3.厦门理工学院电气工程与自动化学院，福建厦门 361000；4.湖南大学电气与信息工程学院，湖南长沙 410000）

0 引言

作为可再生能源利用的关键技术之一，并网逆变器技术对电网的安全运行产生了重大影响。为了有效降低并网逆变器输出电流中的高次谐波，LCL 滤波器因其具有更强的高频谐波抑制能力被广泛采用[1-2]。然而，由于LCL 滤波器的阶数较高，其频率响应中会产生谐振尖峰，因此需要采用阻尼方法来稳定系统[3-5]。相较于通过串并联电阻的无源阻尼方法[6-7]，电容电流反馈有源阻尼无需额外的功率损耗，且对滤波性能影响最小，被广泛应用于抑制系统谐振尖峰[8-10]。在模拟控制中，电容电流反馈有源阻尼等效于在滤波电容上并联1 个电阻。然而，采用数字控制的回路中会引入控制延迟，使其不再等效为简单的电阻，而是1 个随频率变化的虚拟阻抗[11]。文献[12]在考虑控制延时下，推导出临界频率fcrit是采样频率fs的1/6，并且如果LCL 滤波器的谐振频率fr等于fs/6，当采用电容电流反馈有源阻尼时系统无论如何都无法稳定。文献[13-15]进一步分析当fr低于fs/6 的采样频率时，系统必须提供阻尼才能够稳定；如果fr高于fs/6，系统不用进行阻尼也可以稳定运行。由于不可忽略的控制延时，导致数字控制LCL 型并网逆变器的稳定性条件变得更加严格。另外一方面，电网存在感性阻抗，当电网阻抗增大时，会降低LCL 滤波器的谐振频率，使得逆变器很难满足稳定裕度条件，系统对电网阻抗的鲁棒性较差[16-17]。

已有诸多文献提出方案减轻甚至消除数字控制延迟带来的不利影响，以此扩大逆变器稳定区域，提高逆变器对电网阻抗的鲁棒性。文献[18-19]指出数字控制延迟源于数字调制，因此补偿延时不利影响最直接的方法是修改信号采样瞬间或调制波形更新瞬间的顺序。文献[20]将电容电流采样瞬间移到脉宽调制（Pulse Width Modulation，PWM）参考更新瞬间以解决控制延时带来的问题，然而此方法可能会出现混叠错误，进而影响控制器的性能，增加谐波含量。文献[21]表明，采用基于多采样的单电流环控制策略可避免混叠误差，然而该技术主要适用于开关和采样频率较低的大功率应用。另1种方案是采用适当的控制策略间接补偿数字控制延迟。文献[22-23]在电容电流反馈路径中插入1个超前相位补偿器补偿数字控制延迟，扩大了原系统的稳定区域。在文献[24]中，在电容电流反馈路径中插入二阶低通滤波器以增加阻尼稳定区域。文献[25]在系统前向通路中引入相位超前补偿器，同时补偿电容电流采样和并网电流采样的延时。有关电网阻抗和控制延迟对LCL 型并网逆变器稳定性仍需进一步研究。

本文首先建立考虑数字控制延时的单相LCL型并网逆变器系统模型，并基于Nyquist 稳定判据分析并网逆变器对电网阻抗变化的鲁棒性，为此，提出1 种比例-相位滞后补偿策略，使补偿后的LCL 并网逆变器在电网阻抗宽范围变化时都能满足Nyquist 稳定判据，大大提高了并网逆变器对电网阻抗的鲁棒性。最后通过实验结果验证了所提方法的可行性和有效性。

1 考虑时延的并网逆变器数学模型

数字控制LCL 型并网逆变器的系统结构如图1所示。其中，Vdc为直流母线电压，Vg为电网电压，C为滤波电容，L1和L2分别为逆变器侧电感和电网侧电感，Lg为弱电网条件下的电网阻抗，Hi1为电容电流反馈有源阻尼系数，Hi2为并网电流采样系数，这里取Hi2=1，PLL 为锁相环环节，iref为参考指令电流，Gi（z）为准比例谐振（Quasi Proportional Resonant，QPR）控制器，Gd（z）为数字控制延时，在s域下表达式为Gd（s）=e-1.5sTs，SPWM 表示正弦脉宽调制，PLL 为锁相环环节，Gc（z）为相位滞后补偿器，vM为逆变器调制波，Kp为比例系数。采用数字控制不可避免地会引起A/D转换、控制器算法运算、PWM 调制输出等时间延时，SPWM 为如果不考虑这些延时对系统控制器进行设计，不仅会导致系统响应速度变慢，甚至有可能会引起系统不稳定。系统的控制框图可由图1 得到，如图2 所示，其中，vc为电容电压，Kpwm为逆变桥等效增益，其值为Vdc。

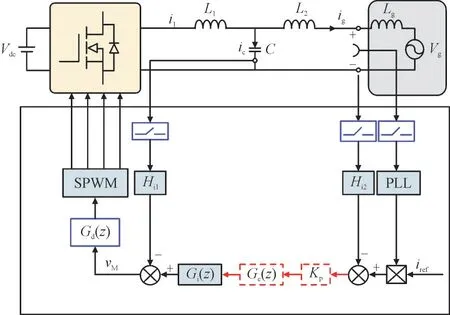
图1 数字控制LCL型并网逆变器系统结构Fig.1 System structure of digital controlled LCL gridconnected inverter

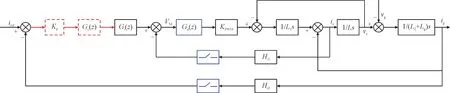
图2 数字控制LCL型并网逆变器控制框图Fig.2 Control block diagram of digital controled LCL grid-connected inverter

由图2 可知系统的开环传递函数Gopen在z域中可表示为：

式中：Z[GLCL（s）]为逆变器调制波vM到并网电流ig在z域中的传递函数。

确保并网逆变器在理想电网中（Kp=1，Gc（z）=1，Lg=0）能够稳定运行，并网逆变器的参数如表1 所示。QPR 控制器在s域的传递函数表示为：

表1 LCL逆变器参数Table 1 Parameters of LCL inverter

式中：Kpr为比例系数；Kr为谐振系数；ω0为基频；ωi为谐振角频率。

参照文献[25]设计了理想电网下电容电流反馈有源阻尼系数和QPR 控制器，即Kpr=0.05，Kr=11.09，ωi=π，Hi1=0.01，Hi2=1。采用零阶保持离散法对式（1）中的GLCL（s）进行离散化，采用Tustin 方法对QPR 控制器进行离散化[26]。理想电网条件下经过有源阻尼和电流控制器补偿之后的环路频率特性如图3 所示。其中，PM为相位裕度，GM为幅值裕度。

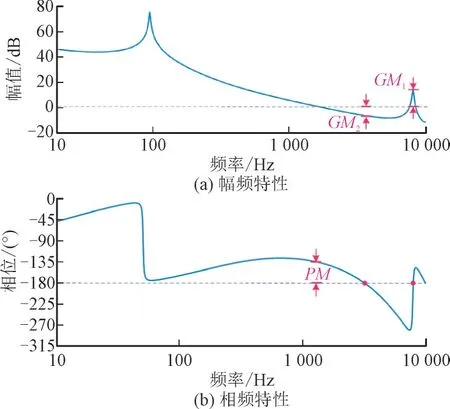
图3 理想电网中Gopen（z）的频率特性Fig.3 Frequency characteristics of Gopen（z）in an ideal power grid

2 系统频域稳定性分析

数字控制延迟在系统开环增益的右半s平面引入一对极点。因此，不能再用传统的相位裕度PM和幅值裕度GM来评估系统的稳定性。相反，应该使用Nyquist 稳定性判据来评估系统的稳定性，如式（3）所示。

式中：N为开环增益的右半s平面的极点数，它映射到z域中表示单位圆外的极点数；C+为bode 图相频曲线由下向上穿越180°（2k+1）线的次数，即正穿越次数；C-为相频曲线由上向下穿越180°（2k+1）线的次数，即负穿越次数。

从图3 可知，N=2，C+=1，C-=0，满足式（3）中的Nyquist 稳定性判据。此时，只有采样频率fs/6 处开环增益小于0 dB，谐振频率fr处增益大于0 dB（即文献[26]中的GM1>0 dB 和GM2<0 dB），系统才能稳定运行。然而，电网阻抗的变化会导致fr发生偏移，如式（4）所示。

式中：ωr=2πfr为LCL 滤波器的谐振角频率。

因此，有必要研究系统的稳定性随电网阻抗变化的情况。

图4 所示为补偿前环路随电网阻抗变化的频率特性。从图4 可以看出，环路在s右半平面有1 对极点，即N=2。在第1 个-180°穿越频率处的增益始终小于0 dB，意味着负穿越始终处于“失效”，即C—=0。另一方面，随着Lg的增大，fr逐渐往左移减小，幅值增益由大于0 dB 变化到小于0 dB，意味着正穿越从“有效”过渡到“失效”，即C+由1 变为0，导致环路不满足式（3）的稳定性判据。

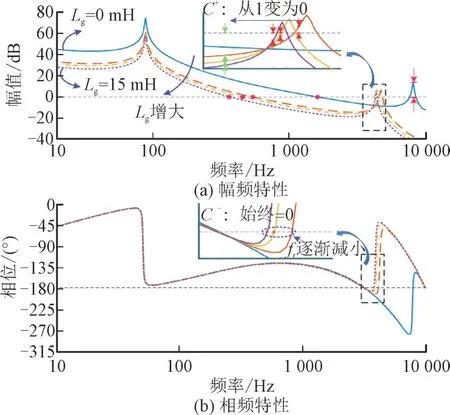
图4 补偿前系统环路随电网阻抗变化的频率特性Fig.4 Frequency characteristics of system loop as the grid impedance changes before compensation

3 补偿策略的设计

3.1 策略设计要求

为了增强系统对电网阻抗的鲁棒性，保证系统在电网阻抗宽范围变化下稳定运行，Gc（z）和Kp的选择应满足以下要求：

1）为了保证重构后的环路在第2 个-180°穿越频率处的增益大于0，即保证C+=1，采用图5 所示的补偿方法：（1）在环路中引入相位滞后，使谐振频率从fr1增加到fr2；（2）增大环路在fr处的增益，即抬高幅频曲线使负增益变为正增益。

图5 比例补偿与相位滞后相结合的补偿方法Fig.5 Compensation method combining proportional compensation and phase lag

2）从图4 可以看出，随着电网阻抗的增大，系统的穿越频率fc减小，基频增益也减小，为了避免稳态误差的增大，可引入比例控制来“抬高”幅频曲线。另一方面，随着电网阻抗的增大，第1 个-180°穿越点逐渐减小，接近fs/6。如果不采取额外措施，系统难以满足在fs/6 处的奈奎斯特稳定性判据而逐渐趋于振荡状态。为此，可引入相位滞后补偿策略，以确保第1 个-180°穿越频率跨越fs/6，有效避免系统在fr=fs/6 时无法满足Nyquist 稳定性准则。由于QPR 控制器的离散化在fs/6 处引入了轻微的相位滞后，在引入补偿策略之前环路的第1 个-180°穿越频率已经发生在fs/6 之前，因此，后续不再进一步分析这一不稳定因素。

3）由于比例系数的加入增大了环路增益，为了避免使C-从等于0 变为等于1，导致不满足式（3）的稳定性判据，比例控制的加入必须满足环路在第1 个-180°穿越频率处的增益始终小于0，即始终保证C-=0。

3.2 比例-相位滞后补偿策略的设计

相位滞后补偿器在z域下的传递函数Gc（z）可表示为：

式中：α为Gc（z）的零点，取值范围为0<α<1。

Gc（z）的频率响应随α值的不同而变化，如图6所示。

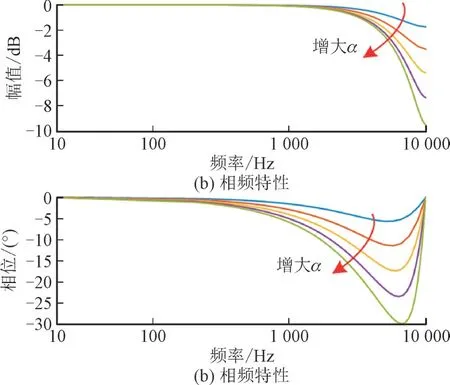
图6 相位滞后补偿器的频率特性Fig.6 Frequency characteristics of phase lag compensator

根据短路比（Short-Circuit-Ratio，SCR）定义[27]，SCR≤10 时的电网被称为弱电网（对应Lg=5.1 mH）。考虑电网阻抗从0 到15 mH 的变化（图4），当电网阻抗Lg=15 mH 时，即可得到所需补偿的最大滞后相位角。并网逆变器参数如表1 所示。

参照3.1 的设计要求，经过相位滞后补偿后的谐振频率需要由fr1变为fr2（图5），其中fr1为补偿前对应的谐振频率，fr2为补偿前开环传递函数在Lg=15 mH 时环路增益为0 dB 对应的频率，fr2计算为3 853 Hz，同时在fr2处对应的相位同样计算为-168°，则由fr1变为fr2需要Gc（z）提供12°的相位滞后，根据式（7）计算出Gc（z）的零点，得到α=0.247；此外，当Lg=15 mH 时，开环增益应保持在0 dB 以上，并留有3 dB 的余量，将此约束与式（1）结合，得到Kp的第1 个约束方程：

当Lg=0 mH 时，可由式（1）计算得到环路在第1 个-180°的穿越频率为f_0mH=2 820 Hz，如3.1 节要求所述，Kp应满足在第1 个-180°穿越频率处的增益始终小于0，得到Kp的第2 个约束方程：

将Lg=15 mH，fr2=3 853 Hz 和Lg=0 mH，f_0mH=2 820 Hz 2 种情况与式（1）、式（6）相结合，分别代入式（8）、式（9），最终得到Kp的取值范围：

折中选取Kp=1.616。

3.3 补偿后系统的稳定性分析

经过补偿后系统的开环频率特性如图7 所示。引入比例-相位滞后补偿后，即使电网阻抗增大，环路在第2 个-180°穿越频率处也始终大于0 dB，同时可以确保环路增益在第1 个-180°穿越频率处不受影响，始终保持小于0 dB，在电网阻抗宽范围变化内都能得到满足式（3）的Nyquist 稳定判据。

图7 补偿后的系统开环频率特性Fig.7 Open-loop frequency characteristics of compensated system

图8 进一步给出了补偿前后电网阻抗变化时闭环系统的零极点分布图。随着电网阻抗的增大，补偿前闭环系统的极点逐渐向单位圆外移动，导致系统不稳定。采用本文提出的补偿策略后，如图8（b）所示，即使Lg增大，极点仍然保持在单位圆内，表明并网逆变器即使在电网阻抗变化很大的情况下也能稳定运行。

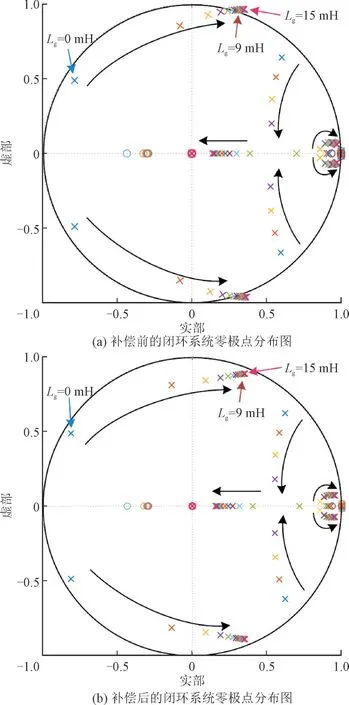
图8 补偿前后电网阻抗变化时闭环系统零极点分布图Fig.8 Zero-pole distribution diagram of closed-loop system when the grid impedance changes before and after compensation

4 仿真与半实物实验验证

4.1 仿真验证

根据表1 参数，在MATLAB/simulink 仿真软件中搭建单相数字控制LCL 型并网逆变器模型，图9给出了并网逆变器在不同电网阻抗下的仿真波形。由图9 可以看出，当Lg=0 mH 时，投入补偿策略前后对并网电流影响甚微；当Lg=9 mH（SCR=5.7）时，并网电流在投入补偿策略后由临界震荡状态迅速恢复至稳定状态，电流总谐波失真率（Total Harmonic Distortion，THD）大大降低；当Lg=15 mH（SCR=3.4）时，投入补偿策略后并网电流由不稳定状态迅速恢复到稳定状态。

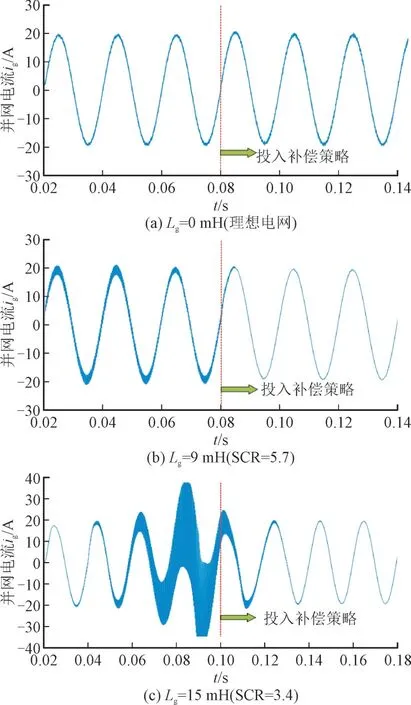
图9 逆变器在不同电网阻抗下的仿真波形图Fig.9 Simulation waveform of inverter with different grid impedance

4.2 半实物实验验证

为进一步验证所提策略对提高系统适应电网阻抗宽范围变化能力的有效性，搭建如图10 所示的远宽能源StarSim HIL 半实物平台，实验参数如见表1。

图10 半实物仿真平台Fig.10 Semi-physical simulation platform

电流环采用电容电流反馈的有源阻尼结合QPR 控制，理想电网下并网电流波形如图11 所示，其中WTHD为THD 值。首先确保并网逆变器在理想电网下稳定运行，并且降至半载运行时，WTHD为2.55%，依旧保持良好的波形。图12 所示为逆变器在不同电网阻抗下的实验波形图。当电网阻抗Lg=0 时如图12（a），与未投入补偿策略的电流环相比，本文所提出的补偿策略对原系统产生的影响很小，表明该策略也适用于强电网。由图8（a）可知，当Lg=9 mH 时，补偿前闭环系统的极点位于单位圆上，处于边缘稳定状态，谐波电流较大。采用本文补偿策略后，单位圆上的极点回到圆内，谐波电流迅速消失，如图12（b）实验波形所示。当Lg=15 mH时，2 个极点在单位圆外，系统处于不稳定状态，如图12（c）所示。经过补偿后并网电流迅速恢复到稳定状态，与理论分析相符。