基于层次分析法加权处理的地震应急物资调度问题优化算法

翟洋嘉 侯金欣

[摘 要]地震通常具有巨大的破坏性，制订有效的地震应急物资调度和决策方案，对于高效有序地完成应急救援工作至关重要。基于地震中应急物资调度的特性，文章建立由时效性、经济性和伤亡性构成的多目标函数，经过阈值法的无量纲处理和层次分析法的加权处理，将复杂的多目标函数转化为单目标函数，进而运用匈牙利算法得到最优资源调度的决策方案。

[关键词]资源调度；运输问题；层次分析法；匈牙利算法

中图分类号：F275 文献标识码：A 文章编号：1674-1722（2024）07-0091-03

★课题项目：国能朔黄铁路发展有限责任公司技术开发项目（GJNY-20-230）

近年来，我国相继发生了多次地震，给国家和人民带来了极大的损失。在目前难以进行有效地震预测的前提下，地震后快速、合理地进行应急资源调度是降低人员伤亡损失、恢复社会秩序的重要途径之一。

震后应急物资调度问题一直是很多学者关注的问题。例如，汪勇等[ 1 ]在考虑需求量和消耗时间的基础上，提出一种灾后多资源调度模型。然而，以上两种模型并未考虑到应急物资调度的伤亡性特性。针对震后应急物资调度具有的时间紧迫、以人为本等特殊性质，相关研究通过构建以时效性、经济性和伤亡性为基础变量的多目标函数，通过无量纲处理和加权处理，将其转换为运输问题或指派问题的单目标函数，继而进行目标函数的求解[2-3]，以上方法为震后应急物资调度方案的优化提供了思路。

目前，震后应急物资调度通常采用主观赋值法加权处理，将多目标函数转换为单目标函数，该方法简单直观，但严重依赖专家经验。层析分析法是一种相对客观的权重处理方法，其将复杂的现实问题分解成多个层次和因素，比较各因素的相对重要性，确定各因素的权重，让决策者对特殊情况、特殊物资的权重进行单独分析，准确确定各级指标的权重，降低传统工作中确定权重过程中的随意性和主观性的成分，保证物资调度的合理性[ 4 ]。

一、构建数学模型

（一）应急资源调度的基本问题设定

地震发生后需转运某应急物资，其中，可提供该物资的库存点有m个，需要该物资的受灾点有n处，物资通过i→j段路线（即从第i个库存点运送到第j个受灾点）所需时间为Tij，对应运价为Pij，第j个受灾点的伤亡密度为Dj。为简化模型，文中应急物资调度问题包括四个基本假定：各物资库存点相互独立，不互相调度资源；运输车辆相同且充足，运输速度保持基本一致；运输过程中不存在堵车情况；各物资库存点的各类应急物资数量充足。

（二）多目标函数的构建

其中，T表示从库存点到受灾点物资调度需要的时间，P表示从库存点到受灾点物资调度消耗的费用，D表示受灾点的伤亡密度。

（三）基本数据确定

在进行无量纲处理前，首先确定资源调度过程中有关时效性、经济性和伤亡性的数值，对于时间和运费的确定，将选择可处理多源最短路径问题的Floyd算法[ 5 ]，在道路网络图上得出物资调度的最长时间Tmax、最短时间Tmin以及最大运费Pmax、最小运费Pmin；对于某时刻的伤亡密度，可以利用中国地震灾害损失评估系统（CEDLAS）进行确定[ 6 ]，得出受灾区的最大伤亡密度Dmax、最小伤亡密度Dmin。

（四）无量纲处理

文章将时效性、经济性和伤亡性看作三个互相独立的变量，考虑到灾害后应急物资调用的特性和方法的简便性，选取阈值法进行无量纲处理。根据上文确定的相关数据，可以得出三个无量纲指标：

（五）基于层次分析法的加权处理

假设地震物资调度不同特性（时效性、经济性、伤亡性）在某段时间内权重保持不变，因此将只考虑地震发生后的t～t+t1时间段内的权重计算，利用层次分析法获取权重的具体步骤如下。

第一，建立n阶判断矩阵A，用Saaty的1-9标度法确定判断矩阵的元素aij，则物资对时效性、经济性和伤亡性的判断矩阵如表1所示。其中，r1代表时效性，r2代表经济性，r3代表伤亡性，矩阵中的数值代表三种特性两两之间相对重要性的比值。

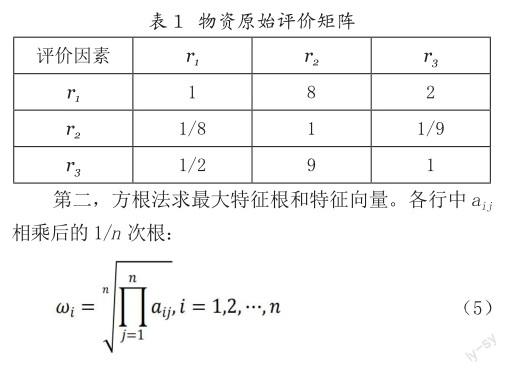
（六）单目标函数模型构建及匈牙利算法

第一，目标函数的构建。

经上述无量纲和加权处理，将多目標函数转化为以下单目标函数：

其中，xij= 1指运输方案中包括i→j段路线，xij= 0指运输方案中不包括i→j段路线，通过求解该式，可得到最大值对应的应急物资调度最优路线。

第二，匈牙利算法。

文章构建的单目标函数可视为指派问题，该类问题可描述为：有m项任务需要n个人承担，由于各人完成任务的效率不同，给出一个分配方案，使工作完成时间最短。匈牙利算法是解决指派问题的一种经典算法，计算效率高，在给定权重的情况下能迅速找到总权重最大的匹配方案。

二、案例分析

（一）数据收集与确定

假设某市突发强地震灾害，人口总量500万人，现有4个物资库存点（A1、A 2、A 3、A4）和4个受灾点（B1、B 2、B 3、B4），物资通过i→j段路线所耗时间为Tij，运费为Pij，地震后第三个小时各受灾点的伤亡密度为Dj，通过上述方法得到以下数据，如表2、表3、表4所示。

（二）无量纲处理

依据公式（2）、（3）、（4），将上述有关时效性、经济性、伤亡性的数据做无量纲处理，得到以下数据，如表5、表6、表7所示。

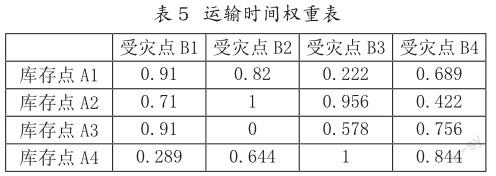
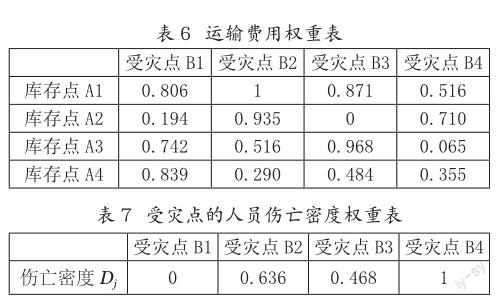
（三）加权处理

运用原始评价矩阵对案例中物资的三种属性进行加权处理，经层次分析法计算，得到该物资关于时效性、经济性、伤亡性的权重向量为μ=（0.57，0.06，0.37）T，可计算得到决策效用函数Eij：

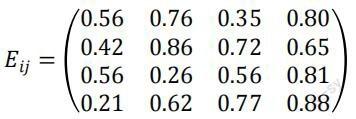
（四）目标函数求解

根据匈牙利算法求解目标函数，可通過E = max-{ Eij}、E0= E -Eij将其化为极小值问题，通过变换初始矩阵E0，求得物资调度的最优路线选择方案。通过变换和计算最终得到：

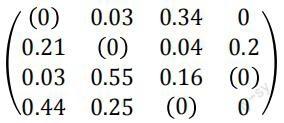
则该物资最优路线选择方案：A1→B1、A2→B2、A3→B4、A4→B3，此时目标函数取得最大值：

s=0.56+0.86+0.81+0.77=3

三、结语

文章针对地震灾害后的应急物资调度问题，综合考虑其时效性、经济性、伤亡性，通过基于阈值法的无量纲处理以及基于层次分析法的加权处理，将多目标函数转化为易于求解的单目标函数，构建了一种简单、可靠的物资调度方案决策算法，以便为地震救援提供科学、有效、及时的帮助。

参考文献：

[1]汪勇，金菲.应急资源调度问题的改进进化规划算法研究[J].运筹与管理，2012（04）：29-33.

[2]徐伟，刘茂，李春志，等.地震期间应急资源调度方案的优化选取[J].数学的实践与认识，2011（06）：30-37.

[3]樊友龙.基于多需求点的突发事件应急物资调度模型研究[D].长安大学，2015.

[4]董君，层次分析法权重计算方法分析及其应用研究[J].科技资讯，2015（29）：218+220.

[5]易小泉.出租车最优路径Floyd算法求解[J].计算机产品与流通，2020（06）：134-136.

[6]郑跃，贺金川，郑山锁，等.中国地震灾害损失评估系统研究[J].自然灾害学报，2020（04）：34-42.