压气机叶片叶根轮槽物理场预测及快速优化设计
2024-04-21赵宇轩陈子峰黄丞明谢永慧张荻
赵宇轩,陈子峰,黄丞明,谢永慧,张荻
(西安交通大学能源与动力工程学院,710049,西安)
压气机是燃气轮机装置的重要组成部分,在压气机的运转过程中,其叶片长时间处在高温、高压的状态下,还受到离心力载荷等复杂的交变载荷作用,这会导致叶片容易产生结构损坏。在燃气轮机的所有故障中,由叶片导致的故障占比达到42%[1]。此外,在各类发动机的零部件损坏事故中,转子叶片损坏占70%以上[2]。可见,叶片是燃气轮机中相当关键的部件,叶片的损坏往往会造成严重事故。
叶根轮槽是叶片与轮盘的连接部分,在工作过程中,其不仅受到离心力等载荷作用,同时在叶根和轮槽的接触区域附近也会产生应力集中,容易引起叶根失效[3]或轮槽开裂[4],从而造成安全事故,因此对叶片叶根和轮槽部位的研究尤为重要。
针对叶根轮槽的主流研究方法为有限元法。国内最早运用有限元法进行分析是在20世纪80年代,陈文伟等[5]、黄秀珠等[6]对汽轮机枞树型叶根轮槽结构进行了弹性有限元分析。沈伟君等[7]在弹性有限元分析的基础上,通过考虑温度场的影响,完善了有限元计算流程。随着计算水平的提高,有限元分析方法日渐成熟。Sinclair等[8]对燕尾型叶根轮槽结构接触特性展开了研究,发现使用凸面加工结构可以减小接触应力。Beisheim等[9]在上述研究的基础上对燕尾型叶根轮槽结构进行了改进。王小平[10]利用变态模型分析了厚度、弹性模量等因素对叶根轮槽接触应力大小和分布的影响。潘燕环等[11]针对风力透平,引入压板法计算等效刚度,讨论了载荷对边界条件和叶根接触状态的影响。以上研究探索了不同因素对于接触状态的影响以及接触状态对叶根轮槽应力分布的影响,为后续叶根轮槽结构的优化设计提供了依据。
针对叶根轮槽结构的优化设计,目前的主流方法是利用有限元分析直接结合遗传算法、粒子群算法等智能优化算法,通过建立优化控制程序调用有限元分析软件进行迭代计算和寻优。吴君等[12]基于三维有限元模型,通过多种优化算法对枞树型叶根轮槽进行了优化设计。Hahn等[13]采用NSGA-Ⅱ非支配排序遗传算法等优化算法对燕尾型叶根轮槽结构进行优化设计。张明辉等[14]进一步考虑了温度载荷的影响,采用模式搜索算法对调节级枞树型叶根轮缘模型进行了优化设计分析。Botto等[15]利用代理模型结合遗传算法,优化了燕尾型叶根轮槽结构。张小娟[16]以三齿枞树型叶根轮槽为研究对象开展优化设计工作,发现基于傅里叶级数-直线法构型的优化算法具有良好的效果。上述针对叶根轮槽结构优化设计所采用的主流方法具有有效性,但也存在一个很大的缺陷,即调用外部软件多次进行有限元分析相当耗时,需要巨大的算力支出。
近年来,深度学习方法在物理场预测领域的应用越来越广泛。Bhaduri等[17]利用深度学习模型预测了机械载荷下纤维增强基复合材料的局部应力分布。Nie等[18]通过使用SCSNet和StressNet架构实现了二维悬臂结构的von Mises等效应力场的预测。Sun等[19]在上述研究基础上,使用改进的StressNet对纤维增强聚合物试样的二维微结构切片进行了应力场预测。Liu等[20]提出了在三维体素微结构体元中预测微尺度弹性应变场的机器学习方法。Yang等[21]开发了一种基于博弈论的条件生成对抗神经网络模型,可以直接从材料微观几何结构中预测应力场或应变场。Lee等[22]使用深度学习方法对未知雷诺数条件下的非定常圆柱扰流模型进行了流场预测。
随着数据驱动方法的进步,人工神经网络[23]、Kriging模型[24]、支持向量机[25]等代理模型已成功应用于叶轮机械的各方面。然而,大部分研究聚焦于叶片本体。此外,将深度学习方法应用于物理场预测领域的研究也主要聚集在流场预测,针对叶根轮槽的物理场预测及结构优化设计研究相对较少。
因此,本文引入了深度学习方法,通过参数化建模的方式建立了压气机叶片叶根轮槽的有限元模型,并基于深度图卷积神经网络建立了叶根轮槽物理场预测模型,实现了从几何结构设计参数到叶根轮槽位移场和应力场分布的映射。基于所构建的物理场预测模型,使用遗传算法对叶根轮槽型线进行优化设计,在保证结果具有足够精确性的前提下,极大地减少了计算成本,加速了计算过程,提高了优化效率。
1 研究对象建立
1.1 模型建立
图1为本文所研究的压气机叶片原始模型及叶根轮槽示意。为节省计算资源,本文选取单扇区周期对称模型进行研究,轮盘左右两侧面为周期对称边界。叶根的齿面和轮槽的齿面紧密相贴,配合完好,在离心力载荷的作用下,二者发生非线性面面接触。压气机叶片和轮盘的材料参数如表1所示。
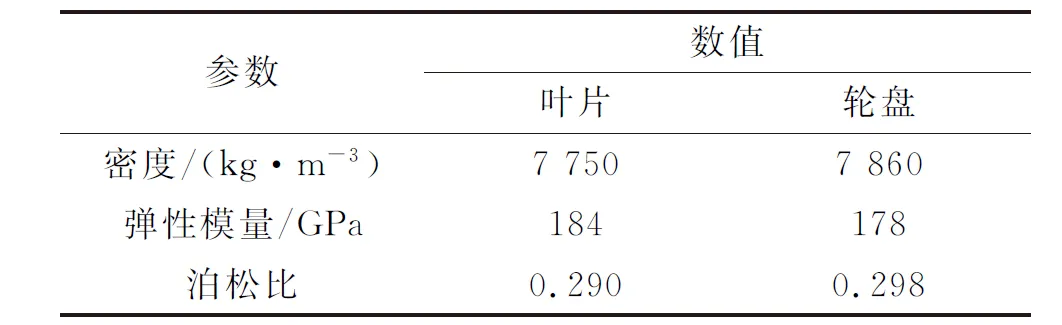
表1 压气机叶片和轮盘的材料参数Table 1 Material parameters of compressor blade and disk

图1 压气机原始叶片模型及叶根轮槽示意Fig.1 Original compressor blade model and schematic diagram of root and groove
1.2 计算条件设置
Meguid等[26]和Song等[27]的研究表明,当叶根轮槽为直槽结构(轴向倾角为0)时,可以忽略其沿轴向的效应,将叶根轮槽结构简化为平面结构,近似采用二维有限元模型研究其物理场分布。图2所示为压气机叶片叶根轮槽的二维有限元模型和边界条件的设置情况。对于二维模型的有限元分析,本文采用4节点四边形单元进行网格划分,同时对接触面附近的网格进行了加密处理,以确保有限元计算的精度。模型的边界条件设置如下。
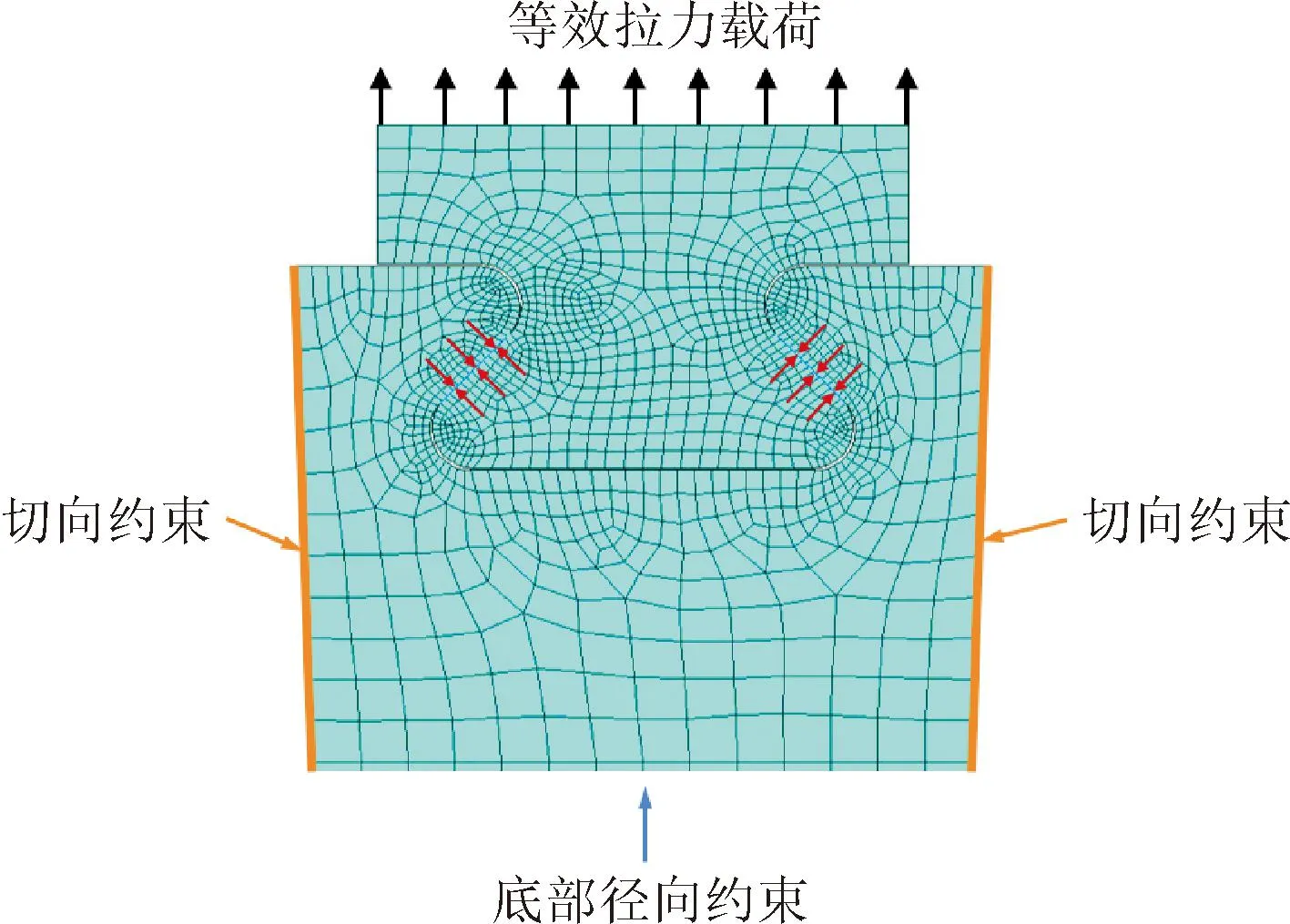
图2 叶根轮槽有限元模型及边界条件设置Fig.2 Finite element model of root and groove and setting of boundary conditions
(1)位移约束。对轮盘周期对称面的节点设置切向约束,对轮盘底部面的节点设置径向约束。
(2)接触对。对叶根与轮槽的接触面建立接触关系,摩擦系数设置为0.2,惩罚系数设置为0.1。
(3)等效拉力载荷。对叶根顶部面施加向上的拉力载荷,其值等于叶身等效的离心力,为23.7 kN。
(4)离心力载荷。对模型整体施加工作转速3 000 r/min对应的离心力载荷,即314.16 rad·s-1的角速度。
(5)温度载荷。对模型整体施加450 ℃的温度载荷。
对比Botto等[15]的研究可知,本文采用上述模型和边界条件所获得的有限元计算结果具有合理性。
2 叶根轮槽的物理场预测
2.1 数据集建立
本文充分考虑压气机叶根轮槽几何结构参数对于应力分布的影响,选取了6个关键尺寸作为设计变量,包括4个叶根参数和2个轮槽参数,分别是:叶根齿内圆角半径R1/mm;叶根接触齿面宽度C/mm;接触齿倾斜角A/(°);叶根齿外圆角半径Rc1/mm;轮槽齿外圆角半径R2/mm;轮槽齿内圆角半径Rc2/mm。图3为压气机叶根轮槽变量选取示意图。
在实际设计过程中,若仅对设计变量的取值范围做出限制,可能会使得创建的模型出现不合理的形状。因此,为了避免这种情况,需要对模型设置一定的几何约束,即对设计过程中的状态变量进行控制。本文对压气机叶根轮槽的设计设置了3个状态变量,分别是:叶根喉部尺寸W/mm,叶根底部面宽度L/mm和叶根高度H/mm。所有参数的初始值及取值范围如表2所示。

表2 叶根轮槽设计变量及状态变量取值范围Table 2 The ranges of design variables and state variables for root and groove
几何约束条件的存在使得各个设计变量不相互独立,因此在采样时需要将几何约束转换成数学形式对设计变量进行判定,剔除不满足约束条件的样本。本文选取3 000个满足几何约束条件的样本,通过ANSYS软件的参数化语言APDL建立参数化模型,并调用有限元计算软件进行网格划分和数值计算,得到神经网络训练所需要的数据集,并按照7∶ 3的比例划分训练集(2 100个样本)和测试集(900个样本)。
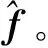

(1)

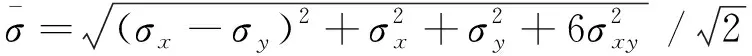
(2)
2.2 预测模型构建及训练
本文采用图卷积神经网络中的GraphSAGE网络[28]对压气机叶片叶根轮槽的物理场建立预测模型,如图4所示。模型整体由空域图卷积SAGEConv构建,包括输入层、中间层、输出层共7层,所有中间层的激活函数都采用GELU函数,损失函数采用SmoothL1Loss,它兼具MAE[29]和MSE的部分优点,适合本文的物理场预测研究,模型的具体结构见表3。模型输入为每个样本的设计变量Θ、节点坐标参数[x,y]T和节点的邻接矩阵A,输出为每个节点的物理场,包括2个位移分量ux、uy和3个应力分量σx、σy、σxy。值得注意的是,图卷积的每层除了接收上层输出的特征外,还需要再次输入节点坐标参数[x,y]T和节点的邻接矩阵A,以充分表征节点的邻接关系。

表3 预测模型网络结构Table 3 Network structure of predictive model
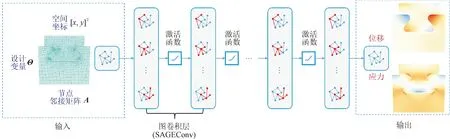
图4 深度图卷积网络模型Fig.4 Deep graph convolutional network model
预测模型构建完成后,还需要设置一些超参数,如学习率、训练集遍历次数等,才能进行模型的训练。本文的训练采用Adam优化算法,初始学习率设置为0.001,训练集遍历次数设为500,并在第300次和第400次将学习率调整为原先的10%,以实现在前期加速训练、在后期保证收敛至稳定状态的效果。模型训练的样本数为采样总数的70%(2 100个样本),训练基于Intel i7-10700 CPU进行。训练过程中损失函数的变化如图5所示。由图可见,损失函数随遍历次数的增加而呈现降低的趋势,且降低速度随次数增加而逐渐减慢,在第150次时已经降低到10-4,并在调小学习率的第300次时趋于稳定,达到最小值4×10-5左右。值得注意的是,在第140次和第210次时,损失函数发生突变,这表明样本中存在很少量的“坏点”(即不合理数据),但随着遍历次数的增加,模型仍能将损失函数降低至10-4以下并收敛,这体现了模型具有很好的鲁棒性。此外,从图中还可以看出测试集和训练集损失函数线基本重合,表明训练过程中未出现过拟合现象。
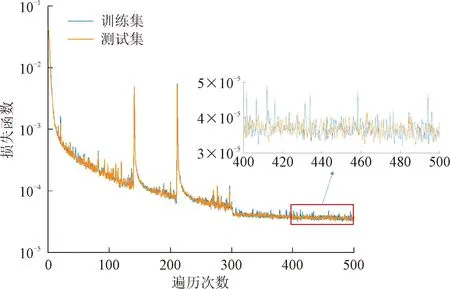
图5 预测模型训练过程损失函数降低情况Fig.5 The reduction of the loss function during the training process of the predictive model
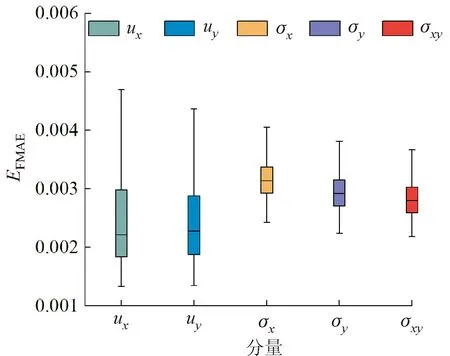
为评估模型对位移场和应力场的预测效果,本文从平均偏差和最大偏差两个角度出发,分别定义了场平均绝对偏差(field mean absolute error,FMAE,用符号EFMAE表示)和场平均最大偏差(field mean max error,FMME,用符号EFMME表示)两个函数来进行衡量。EFMAE定义为每个样本预测各个场偏差的平均值,能反映模型整体的预测情况。EFMME定义为每个样本预测各个场偏差的最大值,能反映模型预测偏差的上界。2个函数的表达式如下

(3)
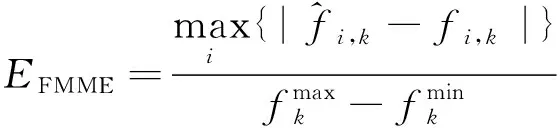
(4)
基于以上定义,图6给出了预测模型的FMAE和FMME指标。由图可见,各预测分量的EFMAE都在0.001~0.005范围内,表明预测模型对整场预测的精度较高,位移场平均最大偏差EFMME在0.007~0.03范围内,应力场平均最大偏差EFMME在0.01~0.07范围内,表明最大偏差也都在可接受范围内。综上所述,本文构建的基于深度图卷积神经网络的预测模型预测精度较高,体现了本文预测方法的有效性。
(a)场平均绝对偏差FMAE
表4为预测模型与有限元方法的计算耗时对比。由表可见,采用构建好的基于深度图卷积神经网络的预测模型进行预测,单个设计方案的耗时在10 ms左右,而利用有限元方法计算耗时在10 s左右,加速效果在103量级,表明本文所构建的预测模型可以实现实时的压气机叶片叶根轮槽物理场参数预测。

表4 预测模型与有限元方法的计算耗时对比Table 4 Comparison of computation time between the predictive model and the finite element method
2.3 位移和应力预测结果及分析
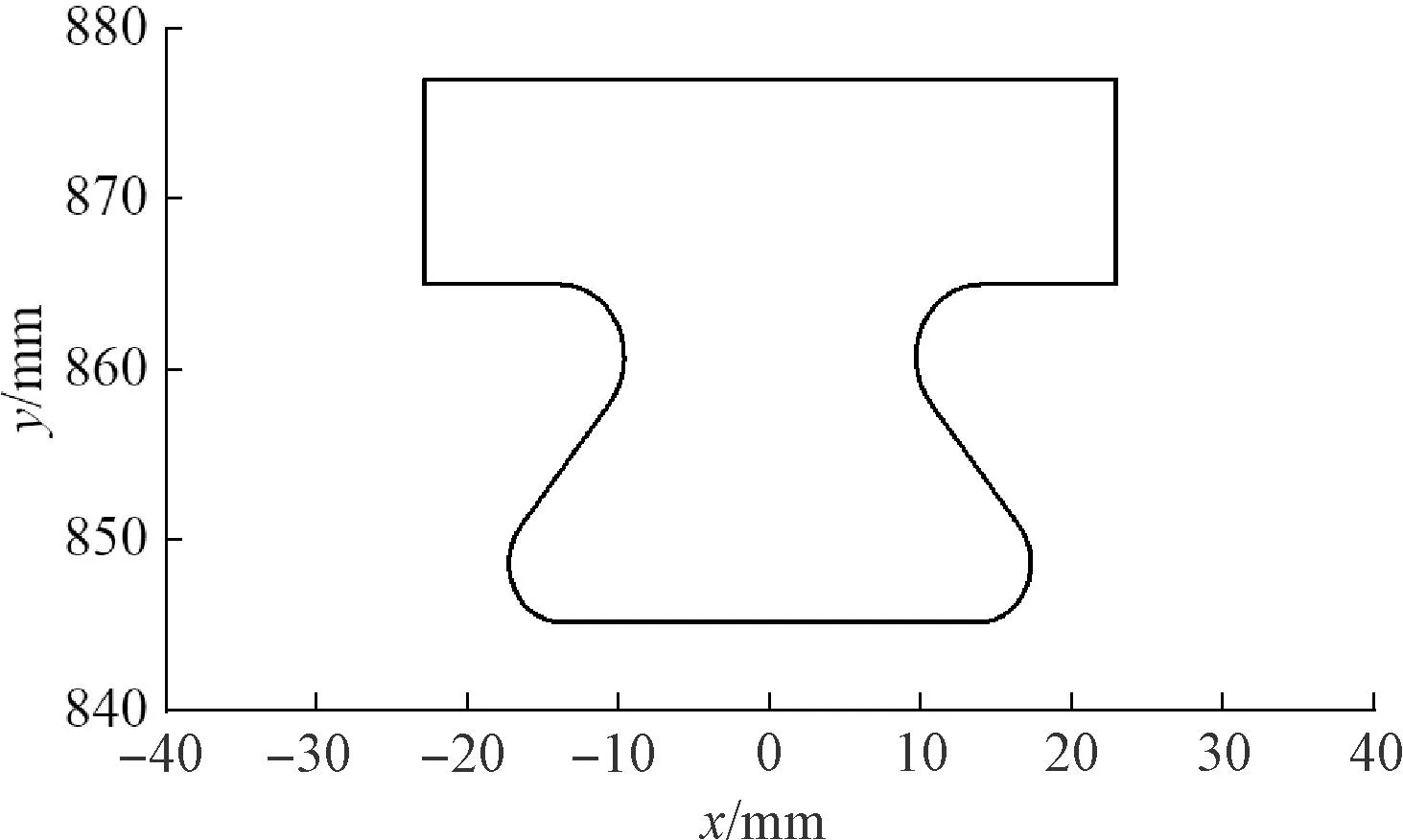
选取测试集中具有代表性的一组设计方案,给出其预测的最大总位移和最大等效应力,并展示总位移和等效应力的有限元分析云图、预测云图和预测偏差分布图,设计方案如表5所示。图7展示了该设计方案对应的几何形状。
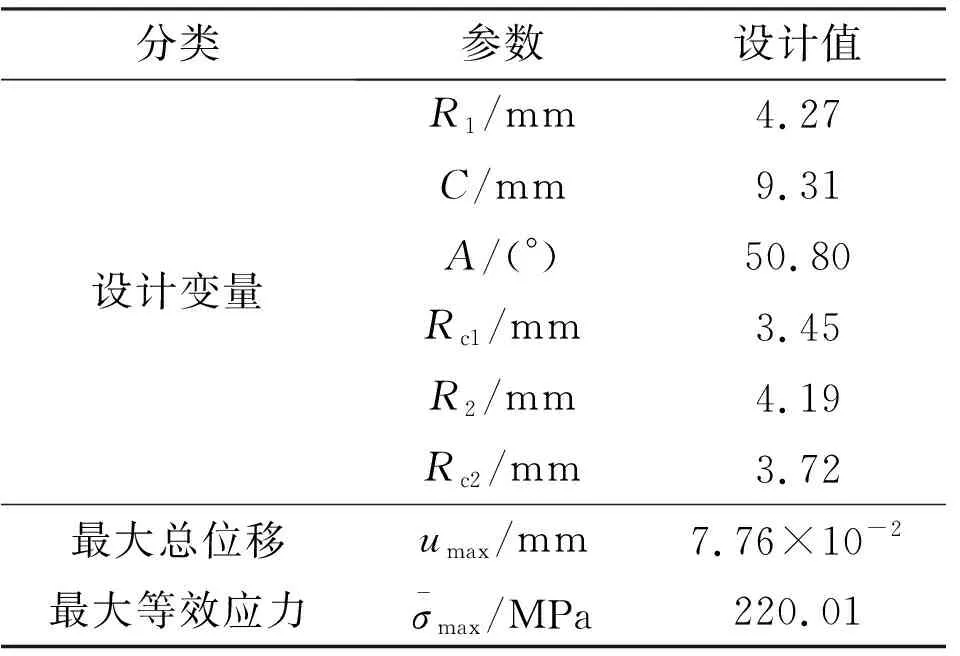
表5 典型设计方案Table 5 Typical design scheme
(a)叶根型线
图8展示了总位移预测结果,图9展示了等效应力预测结果。相比于原始设计方案,该方案的叶根和轮槽圆角半径有所增加,接触齿面宽度和接触齿倾斜角也有所增加。由图可见:总位移最大值为7.76×10-2mm,出现在叶根顶部左侧施加拉力载荷处,相应预测值为7.75×10-2mm,相对偏差为-0.11%;等效应力最大值为220.00 MPa,出现在轮槽右侧齿内圆角处,相应预测值为219.57 MPa,相对偏差为-0.20%。此外,总位移和等效应力沿叶根轮槽型线的有限元分析值和本文模型预测值吻合良好,特别是在分布曲线的波峰和波谷处,预测值的变化趋势与有限元分析值的变化趋势基本一致。
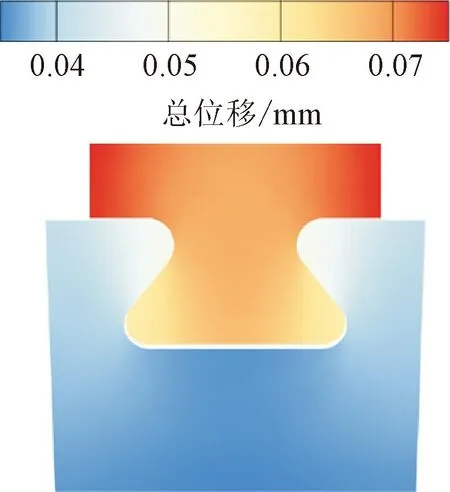
(a)有限元分析总位移分布云图
此外,在所有设计方案中,应力集中现象都出现在叶根齿内圆角和轮槽齿内圆角处,这与实际的压气机叶片叶根轮槽应力分布情况一致。增大叶根齿内圆角和轮槽齿内圆角的半径有助于改善该处应力集中现象,从而降低叶根轮槽区域的最大应力。
除了位移场和应力场的分布情况,工程上一般还关注最大位移值和最大等效应力值。图10给出了最大总位移和最大等效应力的本文预测模型预测结果。由图10(a)可知,在测试集中,叶根轮槽最大总位移的相对预测偏差在1%附近。图10(b)分布频数图表明95%以上的设计方案相对预测偏差都小于1%。图10(c)和图10(d)显示,叶根轮槽的最大等效应力相对预测偏差都小于5%,这表明了本文的研究方法对于最大总位移和最大等效应力的预测具有较高的准确度,能够指导对于叶根轮槽结构的优化设计。

(a)最大总位移预测结果
3 叶根轮槽的快速优化设计
3.1 基于预测模型的优化设计流程
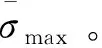
因此,本文最优化问题的实质是找到一组设计变量x=[R,C,A,Rc1,R2,Rc2]T,满足
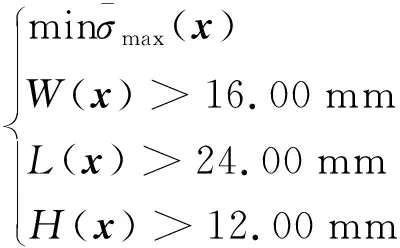
(5)
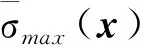
文献[12]指出,在叶根轮槽结构优化问题中,遗传算法具有较好的效果,因此本文采用遗传算法对叶根轮槽进行优化分析,基于预测模型和遗传算法的优化设计流程如图11所示。
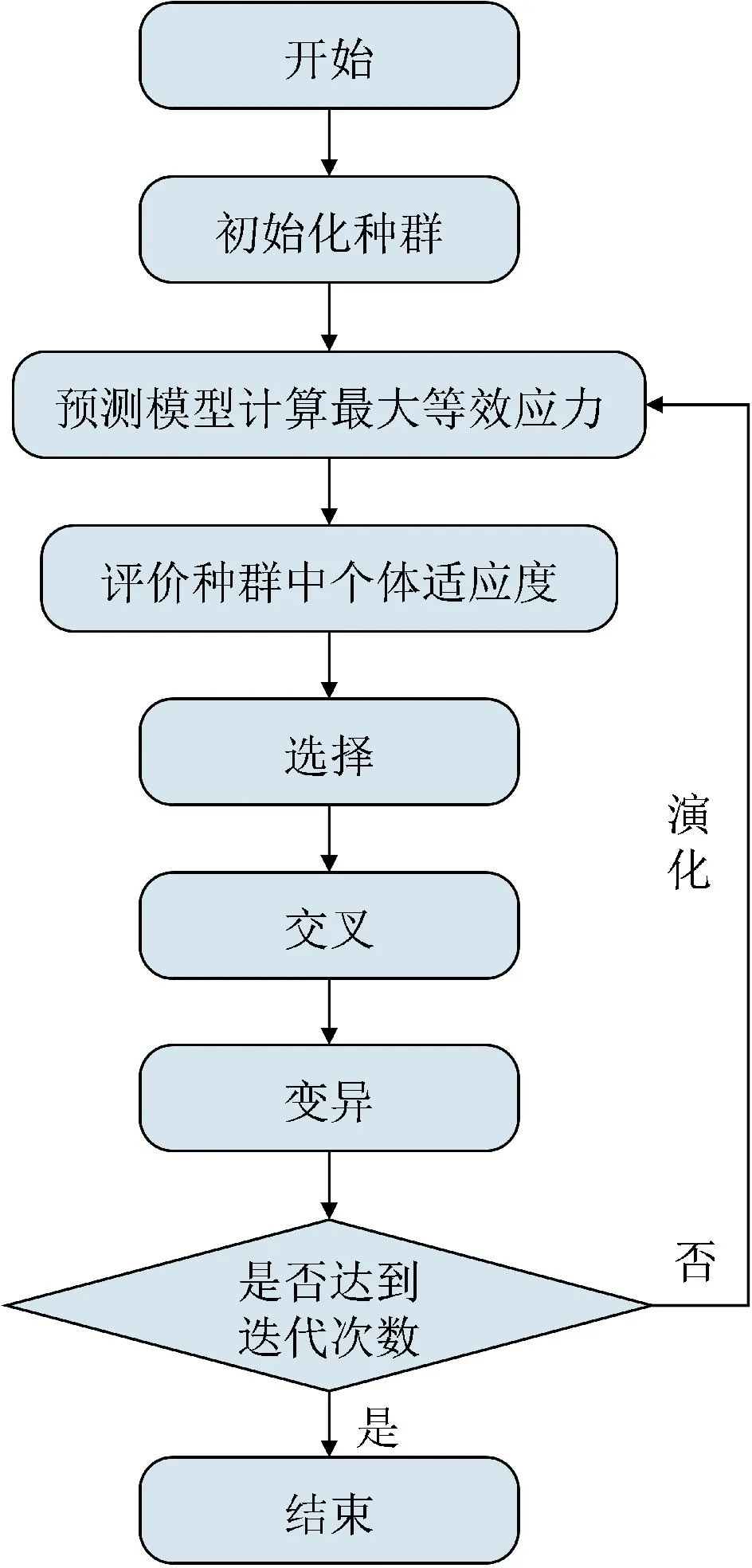
图11 基于预测模型和遗传算法的优化设计流程Fig.11 Optimization design process flowchart based on prediction models and genetic algorithms
3.2 优化结果及分析
在运行优化算法前,需要对遗传算法的相关参数进行设定。本文设置初始种群大小为20,交叉概率为0.2,变异概率为0.1,最大迭代次数设为50,图12展示了运行优化算法后得到的迭代曲线。从图中可以看出,在优化初始阶段目标函数值改善迅速,而在第8次迭代后改善速度放缓,并最终在第25次迭代后趋于稳定,接近最优值213.06 MPa。
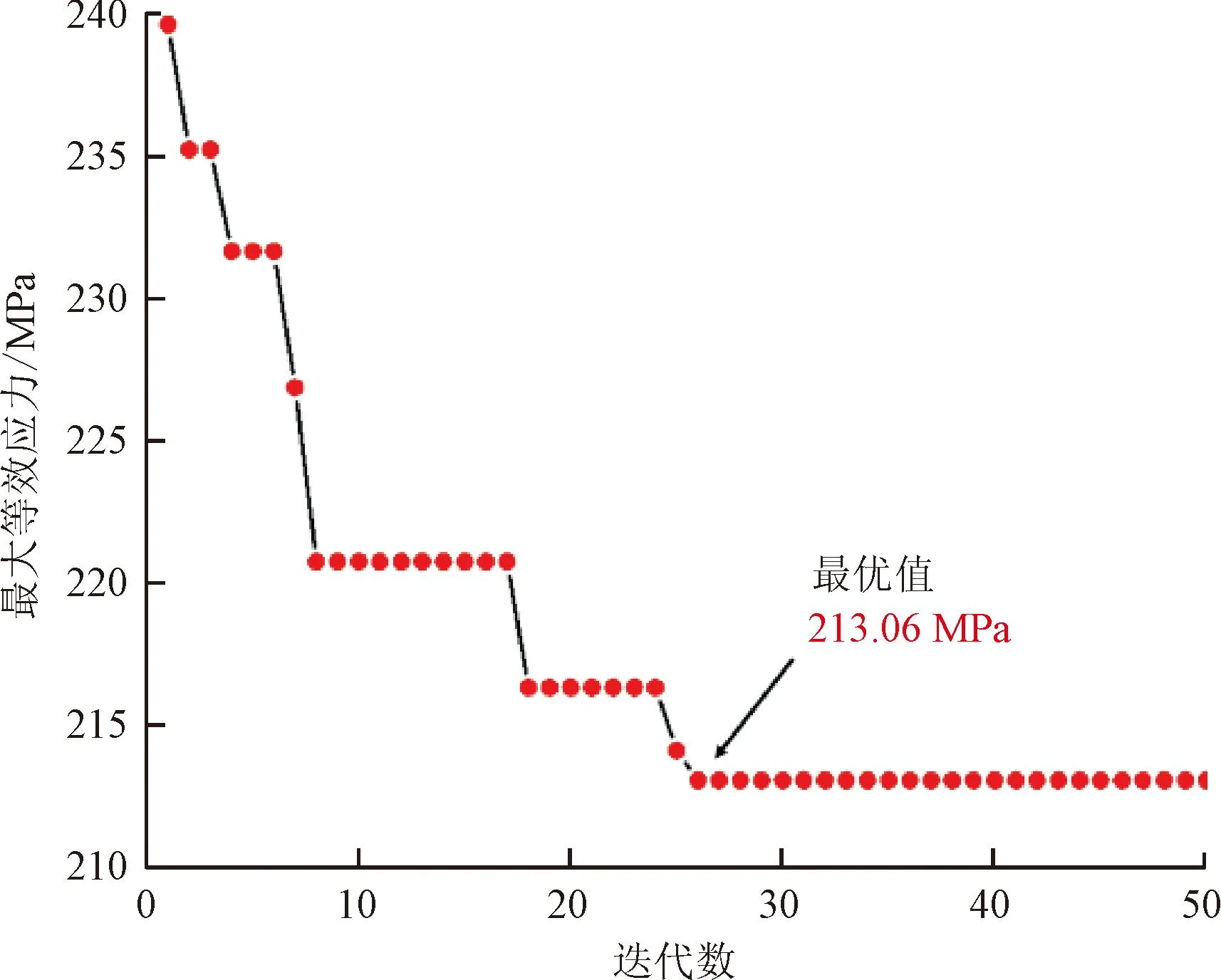
图12 优化目标函数变化曲线Fig.12 Change curve of the objective function during the optimization process
优化前后模型的设计变量如表6所示。从表中可以看出,相比原始的压气机叶根轮槽模型,优化后模型的叶根和轮槽圆角半径显著增大,尤其是叶根齿内圆角和轮槽齿内圆角,而接触齿倾斜角基本保持不变,接触齿宽有所增加,这些设计变量的变化趋势能够对压气机叶根轮槽的优化提供参考。对优化结果进行进一步的分析,图13展示了优化后模型的等效应力预测结果。由图可见,等效应力有限元分析最大值为211.62 MPa,出现在轮槽左侧齿内圆角处,预测值为213.06 MPa,相对偏差为0.68%。此外,等效应力沿叶根轮槽型线的有限元分析值和预测值分布吻合良好,特别是在分布曲线的波峰和波谷处,预测值的变化趋势与有限元分析值的变化趋势基本一致,这表明本文基于预测模型的优化设计方法具有较高的准确度,优化结果的可信度足够高。
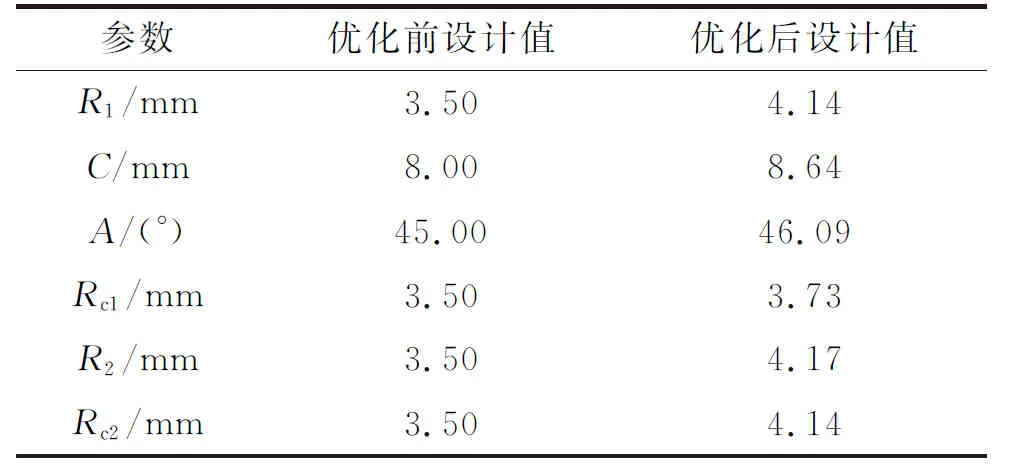
表6 叶根轮槽优化前后模型设计变量取值Table 6 The design variables before and after the optimization of the blade root and groove
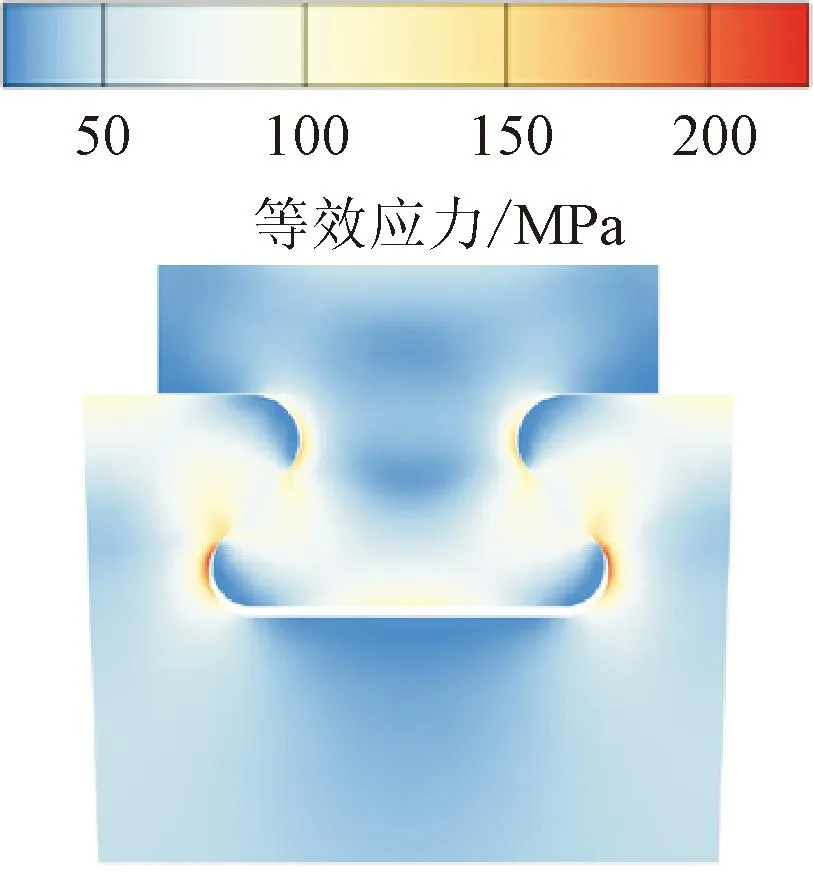
(a)有限元分析等效应力分布云图
3.3 优化前后结果对比及验证
本文将对优化前后的压气机叶根轮槽模型进行进一步的三维有限元分析,并对结果进行对比,以验证优化方法的有效性。三维有限元分析的边界条件设置与二维有限元分析基本一致,区别在于需额外施加两处约束条件:①对轮盘进气侧的节点设置轴向位移约束;②对轮盘出气侧的节点设置轴向自由度耦合。模型整体采用8节点六面体单元进行网格划分,对接触面附近的网格进行加密处理,以确保有限元计算的精度。
图14给出了优化前后压气机叶根和轮槽的等效应力对比云图。由图可见,优化前后压气机叶根和轮槽的等效应力分布基本一致,最大等效应力位于轮槽齿内圆角处。叶根最大等效应力由194.43 MPa降低至159.45 MPa,减小了17.99%;轮槽最大等效应力由240.96 MPa降低至206.37 MPa,减小了14.36%。由此可见,叶根和轮槽的最大等效应力都得到了显著改善,体现了本文优化方法的有效性。
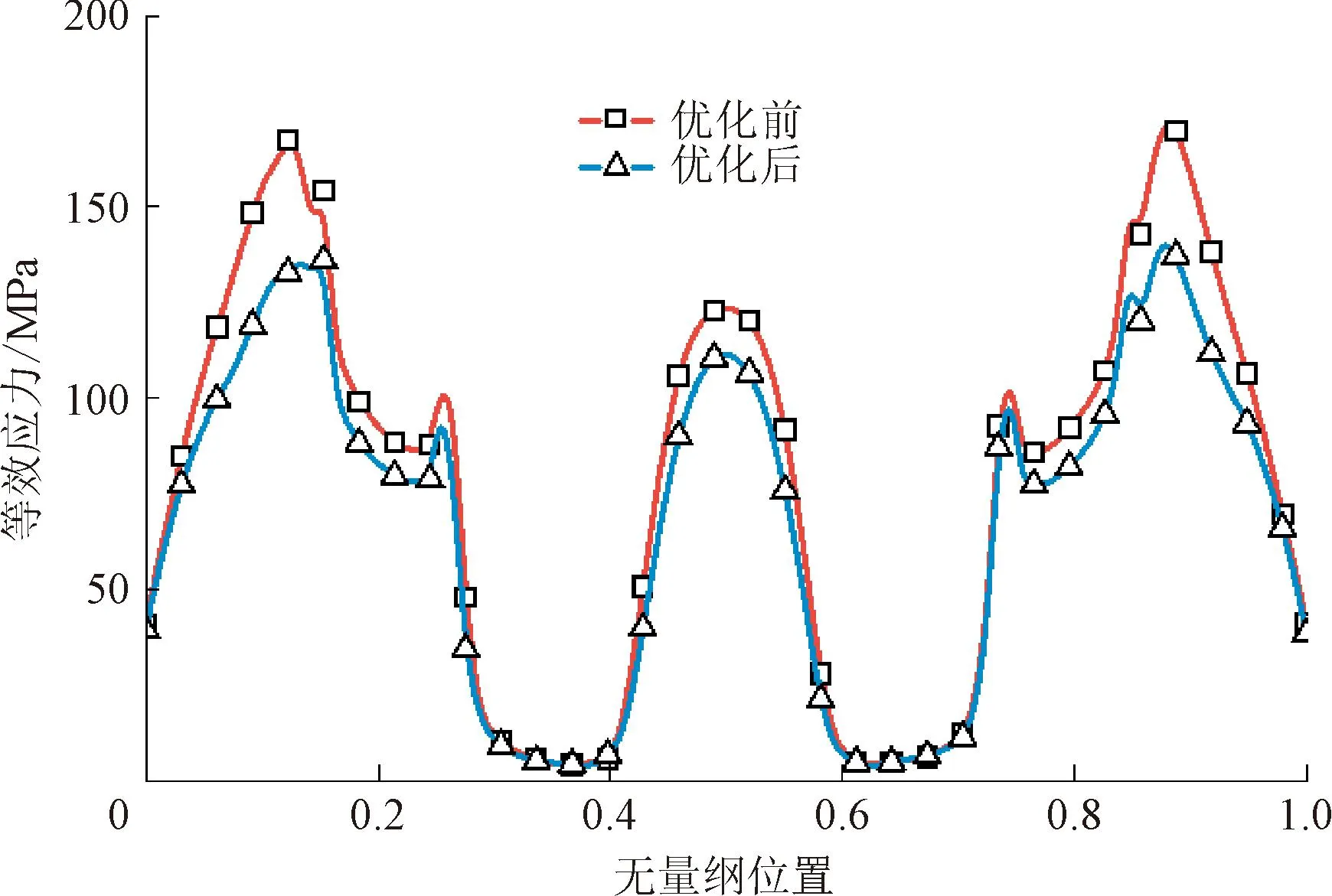
图15给出了优化前后等效应力沿叶根轮槽型线的分布曲线。
(a)等效应力沿叶根型线分布曲线
由图15(a)可见,优化后的叶根型线整体应力水平相比于优化前明显降低,特别是在3个波峰处(即应力集中处)降低幅度最大,这3个波峰分别表示左侧叶根齿内圆角、叶根底部和右侧叶根齿内圆角。由图15(b)可见,优化后的轮槽型线整体应力水平相比于优化前同样明显降低,特别是在左侧轮槽齿内圆角和右侧轮槽齿内圆角这2个应力集中处降低幅度最大。整体看来,经过优化后,压气机叶根轮槽的应力水平大幅降低,优化效果明显。
4 结 论
本文围绕传统叶根轮槽优化设计方法存在的求解过程复杂、计算耗时长、计算成本高等问题,针对压气机叶片叶根轮槽结构,采用参数化建模、深度图卷积神经网络和遗传算法,建立了强度特性快速预测模型和型线优化设计方法,实现了压气机叶片叶根轮槽型线的快速优化设计。本文主要结论如下。
(1)基于参数化建模方法和深度图卷积神经网络GraphSAGE搭建了从压气机叶片叶根轮槽几何结构设计参数到物理场参数的预测模型,实现了由6个设计变量控制的参数化叶根轮槽位移场和应力场的快速准确预测,各物理场分量的平均绝对偏差EFMAE都在0.001~0.005范围内,位移场平均最大偏差EFMME在0.007~0.03范围内,应力场平均最大偏差EFMME在0.01~0.07范围内,表明预测模型对整场预测的精度较高。此外,预测模型相比于有限元计算的加速效果达到103量级,表明所构建的预测模型可以实现快速压气机叶片叶根轮槽物理场参数预测。
(2)进行了参数化压气机叶片叶根轮槽物理场的快速预测,结果表明,位移和应力预测值的变化趋势与有限元分析值的变化趋势一致,最大总位移的相对预测偏差在±1%范围附近,最大等效应力相对预测偏差都在±5%范围内,预测结果具有较高的准确度,能够用于叶根轮槽型线的优化设计。
(3)基于所构建的压气机叶片叶根轮槽物理场预测模型,以最小化叶根轮槽最大等效应力为目标,采用遗传算法进行了型线的优化设计分析,同时对优化前后的叶根轮槽模型进行了三维有限元分析和对比,结果表明,优化前后叶根和轮槽的等效应力分布基本一致,最大等效应力位置也基本不变,但数值大幅降低,叶根轮槽整体结构的最大等效应力值由240.96 MPa降低至206.37 MPa,减小了14.36%。此外,优化后结构的等效应力在应力集中处降低幅度最大。由此可见,压气机叶片叶根和轮槽的最大等效应力都得到了显著改善,体现了本文优化方法的有效性,能够实现压气机叶片叶根轮槽型线的快速优化设计。
