NC-OFDM雷达通信一体化设计
2024-04-20朵琳,刘毅
朵 琳, 刘 毅
昆明理工大学 信息工程与自动化学院, 云南 昆明 650504
军用领域和民用领域对于雷达和通信的需求都日益强烈。传统上,雷达和通信系统是分开设计和部署的,分别用于目标探测和数据传输,而随着技术发展和需求的变化,雷达通信一体化的概念应运而生,雷达与通信两者系统硬件和射频前端架构相似,也为联合雷达与通信系统一体化提供了理论基础。雷达和通信一体化通过共享硬件与资源,提高系统的效率和功能,在同一设备上完成目标探测和通信功能,不仅可以提高频谱利用率,更可以提高硬件利用,减少设备使用空间,降低制造成本,在军事、航天航空、车联网、智能家居等领域有着广阔的发展前景,因此,雷达通信一体化具有十分现实的研究意义。
雷达通信一体化主要有两种设计思路:一种是基于通信的波形实现雷达感知的功能,例如正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM),正交时频空间(Orthogonal Time Frequency Space,OTFS);另一种是将通信的信息嵌入到雷达波形中,例如调频连续波(Frequency Modulated Continuous Wave,FMCW)[1]。其中,基于通信波形的一体化设计具有易于实现、通信系统稳定、资源利用率高、抗干扰能力强等优势[2]。
以通信为中心的一体化波形设计,主要将通信信号进行脉冲化,以达到雷达探测的目的,其中以OFDM波形为主要研究方向[3]。OFDM是一种典型的多载波传输方案,具有频带利用率高、抗干扰能力强、易于实现等优点,在通信和雷达探测中都有重要的应用。文献[4]结合直接序列扩频编码和OFDM进行波形设计,并通过检测模糊函数和自相关函数分析了设计波形的性能;文献[5]采用格雷码技术来改善OFDM峰值平均包络功率比(Peak-to-Mean Envelope Power Ratio,PMERP)问题,同时选择最佳循环序列来提高一体化波形的低峰值旁瓣比(Peak-to-sidelobe Level Ratio,PSLR)。
以上研究均是在连续频谱条件下展开的,本文为提高频谱利用效率,研究非连续谱中的雷达通信一体化技术,结合认知无线电(Cognitive Radio,CR)思想[6],提出以非连续正交频分复用(Non-Contiguous OFDM,NC-OFDM)信号作为雷达通信一体化信号,以缓解现如今频谱资源紧张的问题,并研究其雷达探测性能及无线通信性能,以期为雷达通信一体化在非连续谱中的设计带来参考。
1 基于NC-OFDM的一体化方案设计
1.1 NC-OFDM
认知无线电的核心思想是CR系统具有学习能力,通过与CR用户当前的周围环境进行信息交流,感知频段的利用情况,选择可用的频谱资源,并限制或降低冲突的发生。CR用户进行通信传输时,会对子载波进行选择性使用,将被占用的子载波置零,选择闲置的子载波进行数据传输。由于进行数据传输时,频段的可用子载波是随机且不连续的,因此把这种不连续的OFDM通信技术称为非连续正交频分复用(NC-OFDM)技术[7]。
1.2 雷达通信一体化框架
基于NC-OFDM雷达通信一体化的流程如图1所示。

图1 NC-OFDM雷达通信一体化方案系统框图
系统通过动态频谱感知获得当前时刻的频谱使用情况,然后根据频带中频谱使用情况,选择合适的子载波进行数据传输,当子载波i对应的频点不可使用时,令ai=0,当子载波i对应的频率点可以使用时,令ai=1,得到频谱效用序列A=(a0,a1,…,aN-1)。
在发射端,二进制比特数据流通过正交幅度调制(Quadrature Amplitude Modulation,QAM)后得到符号数据,将符号数据按照频谱效用序列A依次对应放于其中不为零的位置,再经过离散傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT)得到时域信号xi(i=0,1,2,…,N-1),再经过并/串转换成串行符号数据,将循环前缀添加到单个OFDM符号前,得到时域NC-OFDM信号,最后经过射频前端发射到信道中传输至接收端[8]。
NC-OFDM发射信号x(t)可表达为
(1)
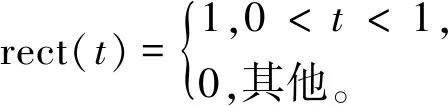
接收端将收到的信号y(t)分两路处理:接收端一路信号送至通信处理端,去掉循环前缀后进行串/并转换,再通过快速傅里叶变换(Fast Fourier Transform,FFT)将信号变换到频域,然后按照频谱效用序列A,将A中不为零对应位置的符号取出得到符号数据,最后通过并/串转换和QAM解调得到二进制数据;接收端将另一路信号去掉循环前缀和串/并转换后,经过快速傅里叶变换变换到频域,得到接收调制符号序列,再送至雷达处理端进行目标探测处理。
经过多普勒频移后,雷达接收信号为
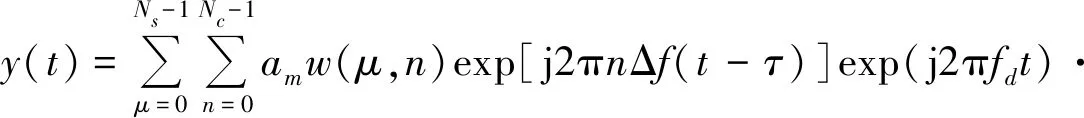
(2)

1.3 雷达处理算法
由发送信号和多普勒频移表示可得到接收调制符号:
(3)
调制符号帧矩阵形式为
(4)
其中,每一列代表一个NC-OFDM符号,每一行代表一个子载波,即纵轴为频率轴,横轴为时间轴。将频域符号重新排列在时频二维空间中。
为降低通信信息对于雷达探测的影响,可以通过将接收调制符号矩阵与发射信号调制符号进行按元素的复数除法:
(5)
即为比较接收频域符号矩阵(Dm)μ,n与发射频域符号矩阵(Dw)μ,n得到的信道的频域传输函数,相除之后只剩下距离因子kR(n)和多普勒因子kD(μ)。
将发射调制符号w(μ,n)和接收调制符号m(μ,n)代入公式(5),得到
(6)
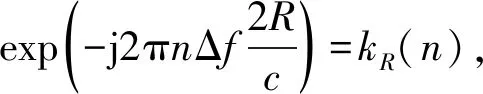
(7)

(8)
其中,μ=0,…,Ns-1;n=0,…,Nc-1。
向量kR和向量kD在接收符号矩阵中分别描述反射物的距离和多普勒频移带来的相移。
对于一个与一体化发射端距离为R的物体,所有反射NC-OFDM符号的子载波数据间都将产生一个线性位移。假设物体是静止的,对于同一个NC-OFDM符号,即同一时间点,距离信息R被包含在频率轴上的调制符号间的线性相移中,对kR(n)做非均匀逆快速傅里叶变换(Inverse Non-uniform Fast Fourier Transform,INUFFT)即可提取出距离信息[9]。
速度处理与距离处理相似,以相对速度vrel运动的目标反射的回波信号的多普勒频率是具有同样相对速度的通信信号的多普勒频率的两倍。对于同一个NC-OFDM子载波,即同一频率点,相对速度信息vrel被包含在时间轴上的调制符号间的线性相移中,通过对kD(μ)非均匀快速傅里叶变换(Non-uniform Fast Fourier Transform,NUFFT)提取速度信息。
1.4 一体化信号模糊函数
模糊函数(Ambiguity Function)是分析雷达探测性能的有效工具,通过模糊函数图可以有效反应雷达测量精度及抗干扰能力[10]。
雷达信号的模糊函数表达式为
(τ,fd)=s(t)s*(t-τ)exp(j2πfdt)dt,
(9)
其中,τ为时延,fd为多普勒频移,*表示共轭。
根据公式(3)和公式(9),可以得到NC-OFDM一体化信号模糊函数的表达式为

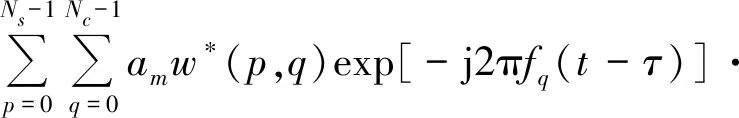
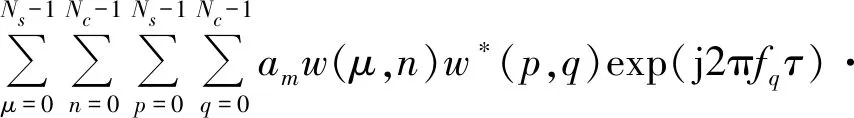

(10)
其中,Tmin=max(μTOFDM,pTOFDM+τ),Tmax=min[(μ+1)TOFDM,(p+1)TOFDM)。
由定积分计算公式可知:

(11)
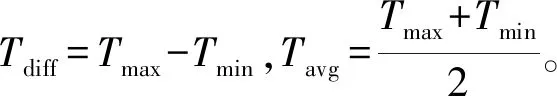
将公式(11)代回公式(10),则公式(10)可以改写为
sinc[π(fq-fn-fd)Tdiff]exp[j2π(fn-fq+fd)Tavg]。
(12)
当τ=0,fd≠0时,可得速度模糊函数为
exp[j2π(fn-fq+fd)Tavg];
(13)
当τ≠0,fd=0时,可得距离模糊函数为
sinc[π(fq-fn)Tdiff]exp[j2π(fn-fq)Tavg]。
(14)
由式(14)可明显看出,一体化波形的模糊函数不仅受时间延迟τ和多普勒频移fd的影响,也受通信调制信息w(μ,n)的影响。
1.5 NC-OFDM一体化信号自相关特性分析
NC-OFDM系统先通过频谱感知得到频谱效用序列A。A中数值为1的位置为可用频点,数值为0的位置为不可用频点。NC-OFDM系统在可用频点上传输数据,而不可用点上不传输数据。造成了系统信号频谱出现空洞,使得NC-OFDM自相关性能受到影响。为了研究频谱空洞对于信号自相性的影响,本文仿真了当NC-OFDM系统关闭子载波的比例分别为1/4、1/2、3/4情况下的信号自相关特性,结果如图2所示。

(a) 1/4子载波关闭
由图2(a)可知,当1/4子载波为0时,次峰峰值远小于主峰;而从图2(b)、(c)可以看出,当随着子载波关闭比例增大,次峰峰值越来越逼近主峰,可见频谱的空洞会影响到NC-OFDM信号的自相关性能。
2 一体化波形设计
传统雷达波形设计的目的是得到具有最优自相关特性的波形来保证雷达探测性能,通信波形的设计是要保证能对抗各种信道衰落及多用户干扰,从而准确地解调解码出通信信息,两者存在较大的差异,需要设计合适的波形以同时实现信息传递和目标探测功能[13]。本文利用选取互信息作为感知和通信一体化信号设计指标,并对通信和雷达的互信息加权来实现一体化波形设计。
2.1 雷达互信息模型
接收端接收到第p个脉冲回波信号为
yp(t)=x(t)*h(t)+np(t),
(15)
其中,h(t)为目标脉冲响应(高斯随机过程),*表示卷积运算,np(t)为附加性零均值高斯白噪声。
接收信号与目标脉冲响应间的互信息为
(16)
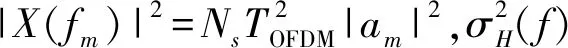
利用接收信号与目标脉冲响应间的条件互信息来作为评估雷达目标分类性能的指标,即
(17)
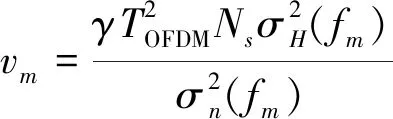
2.2 通信数据率模型
根据香农公式可知通信信道容量为
(18)

2.3 最优化雷达通信一体化波形设计
以通信和感知互信息的加权和为目标,最大化互信息与通信数据率,实现感知通信一体化信号波形的设计与优化,可得到最优化数学模型:
(19)
其中,Wr为雷达加权系数,Fr为最大互信息,Fc为最大通信数据率。
2.4 迭代优化算法
极小化-极大化(Minorization-Maximization,MM)优化算法主要用来解决一些难以直接处理的优化问题,其思想在于将复杂问题转化为一系列简单问题,求最大化函数f(x),实际优化一组以g(x)为主函数的近似目标函数,通过多次迭代优化直至满足条件。
利用该算法进行优化求解步骤如下:
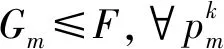

4)令k=k+1,计算更新迭代解,重复步骤2),直至满足收敛条件。
最终得到闭式最优解为
(20)

3 仿真性能与分析
3.1 雷达探测性能仿真
3.1.1 模糊函数
为了验证一体化信号的雷达性能,本文仿真了NC-OFDM一体化信号模糊函数。其中,发射信号的载波频率为24 GHz,OFDM符号周期TOFDM=1 μs,子载波数Nc=16,子载波间隔频率Δf=10 kHz,仿真结果如图3所示。从图3(a)可以看出,NC-OFDM一体化信号的模糊函数图形接近于图钉形,说明其具有一个良好的雷达探测性能。进一步分析,从图3(b)可以看出其主峰时延模糊约为0.12 μs,次峰高度为0.2;从图3(c)可以看出其主峰多普勒模糊为2 MHz,次峰最高为0.22左右,相对于主瓣,两者旁瓣都较低,进一步证实上文所说NC-OFDM一体化信号具有良好的雷达探测性能,同时表明了NC-OFDM一体化信号具有较高的距离、速度分辨力。
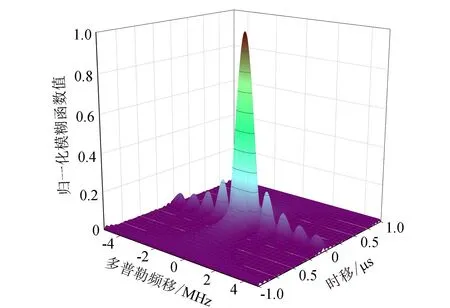
(a) 模糊函数图
3.1.2 距离分辨率和方位分辨率
为研究子载波部分关闭条件下雷达成像性能,本文仿真了1/4、1/2、3/4子载波关闭及子载波不关闭4种情况下距离分辨率和方位分辨率性能变化,仿真结果见图4。

(a) 距离分辨率 (b) 方位分辨率
由图4可知,当子载波关闭时,导致距离分辨率增大和方位分辨率降低。这是由于子载波的关闭意味着在特定的频率上没有传输信号,这会导致有效的频率带宽减小,从而增大距离分辨率。距离分辨率是雷达系统中用于分辨两个目标之间的最小距离的能力。当子载波关闭时,有效的频率带宽减小,相应地距离分辨率变大,使得雷达无法准确地分辨两个距离较近的目标,而会将它们视为一个更大的目标。
子载波的关闭也会对方位分辨率产生影响。方位分辨率是雷达系统中用于分辨目标在方位角上的能力。当子载波关闭时,相应的方位信息无法获取,从而降低了方位分辨率,使得雷达无法准确地分辨两个在方位角上接近的目标,而会将它们视为一个更宽的目标。因此,在雷达成像应用中,需要考虑子载波的关闭对成像分辨率的影响,并根据具体需求和性能要求进行选择与优化。
3.2 无线通信性能仿真
3.2.1 不同比例子载波置零下误码率
为分析子载波在不同关闭比例下误码率情况,本文分别仿真了当10%、15%、25%的子载波关闭下在AWGN信道下的系统误码率,仿真结果如图5所示。
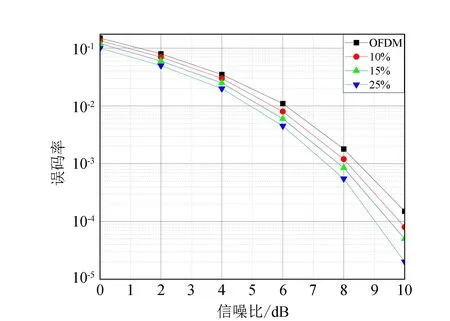
图5 不同比例子载波关闭下误码率
从图5可以看出,NC-OFDM的误码率明显优于OFDM,而且随着子载波关闭的比例增大,误码率逐渐降低。这是由于NC-OFDM系统与OFDM系统仅在子载波的使用上存在差异,但子载波的关闭没有产生信息的丢失,关闭部分子载波后反而消除了相应频率上的噪声,从而使得随着子载波的关闭,NC-OFDM误码率降低。
3.2.2 不同调制方式下误码率
为进一步分析一体化信号的误码率情况,本文仿真了NC-OFDM子载波关闭比例为1/4情况下,分别采取QPSK、16QAM、64QAM调制,对NC-OFDM和OFDM在AWGN信道下的系统误码率性能进行仿真。仿真结果如图6所示。

图6 不同调制方式下误码率
从图6可以看出,不同调制下的NC-OFDM信号的误码率性能都优于采用同样调制下的OFDM信号,其中QPSK调制下的NC-OFDM信号的误码率性能最好,而采用64QAM调制的OFDM信号的误码率性能最不理想。说明NC-OFDM系统较OFDM系统在误码性能上有所提高。
4 结论
本文针对频谱资源愈加紧张的现实情况,基于认知无线电的思想,提出了NC-OFDM雷达通信一体化信号的设计方法,并构架了NC-OFDM一体化系统结果,分析了一体化信号的自相关性能和模糊函数,并用互信息作为指标,运用主优化算法进行波形优化设计。通过仿真,对比OFDM雷达通信一体化信号,NC-OFDM雷达通信一体化信号具有接近图钉型的模糊函数及更低的误码率,证明了其具有良好的雷达探测及无线通信性能,表明了本文所提出的NC-OFDM雷达通信一体化信号是一种性能优良的一体化信号。
