多IRST自适应协同定位技术研究

张 磊, 刘 莎, 王合龙, 程小亮

(1.中国航空工业集团公司洛阳电光设备研究所,河南 洛阳 471000; 2.空装项目中心,北京 100000)

0 引言

机载雷达能够灵活地进行大范围态势感知,但是其电磁信号易被敌方捕获,遭受到敌方电磁干扰甚至武器打击[1-2]。红外搜索与跟踪(Infrared Search and Tracking, IRST)系统被动接收目标红外辐射,可获取目标高精度角度信息,然而由于其被动工作方式,无法获得目标距离和速度信息[3-4]。

单一IRST因观测度不足,难以在实战应用中提供有效态势信息。多IRST协同定位技术可综合利用多IRST探测信息,按照一定准则进行分析、综合与协调,进而克服单IRST的随机性和局限性,显著提高空战战场态势感知能力[5-6]。但是,多IRST信息融合系统信息量巨大,需要实时完成多IRST信息处理,实现在不同态势环境下自主完成协同决策[7]。

针对上述问题,文献[8]提出了一种多机协同机载无源定位技术,并进行了几何精度因子(GDOP)分析,该技术虽然解决了单机无源定位响应时间长的问题,但其对量测信息直接进行扩维融合,引入了高阶矩阵,计算量增加,对系统通信带宽要求较高;针对数据级融合计算量大的问题,文献[9]提出了一种基于分布式融合策略的协方差凸组合融合算法,对局部跟踪进行航迹融合,减小了运算量,但其凸组合算法仅对各传感器局部估计进行自适应融合,并未形成闭环反馈,将融合结果反馈至各传感器;针对子滤波器滤波结果全局最优融合问题,文献[10]提出了基于联邦UKF算法的多机协同无源定位,实现了高精度无源定位,但其子系统仅为单架载机,UKF算法只能进行角度滤波,距离信息需引入其他传感器信息;文献[11]针对无源定位仅有视线角量测的不足,提出了基于联邦EKF的多机协同无源定位技术,该技术首先确定双机定位子系统,在双机定位的基础上进行联邦滤波,进而扩展为多机协同定位算法,提高了定位系统的容错性能,但是该算法对于高度非线性化的系统,效果并不理想。

针对上述不足,本文提出了基于GDOP的多IRST自适应协同定位技术。GDOP可用于衡量测向定位精度,GDOP 值越小,定位精度越高。将GDOP作为优化指标,依据GDOP值实时构造面向定位精度的信息类函数,进而确定信息分配系数,该算法可保证定位精度高的组合在信息融合中所占权重较大,进而保证定位结果的准确性。本文采用自适应联邦UKF算法对子系统局部估计进行信息融合,自适应联邦滤波利用子滤波器处理子系统的信息,在得到各子滤波器的局部估计后,基于GDOP的信息分配原则通过全局滤波器实现所有子系统的信息融合,最后用全局滤波解来重置各子滤波器和主滤波器的滤波值和估计误差方差矩阵。该算法在保证定位精度的同时,相比集中式信息融合减少了数据通信量,可有效隔离错误数据,保证了系统的稳定性。

1 测向交叉定位原理

测向交叉定位原理为通过三维空间内测向射线交叉确定目标位置[12]。IRST测角精度高,为得到目标高精度位置信息,需采用两个或两个以上IRST进行协同探测,根据载机间距离及探测角度信息进行三角解算,从而确定目标位置,双IRST测向交叉定位原理如图1所示。

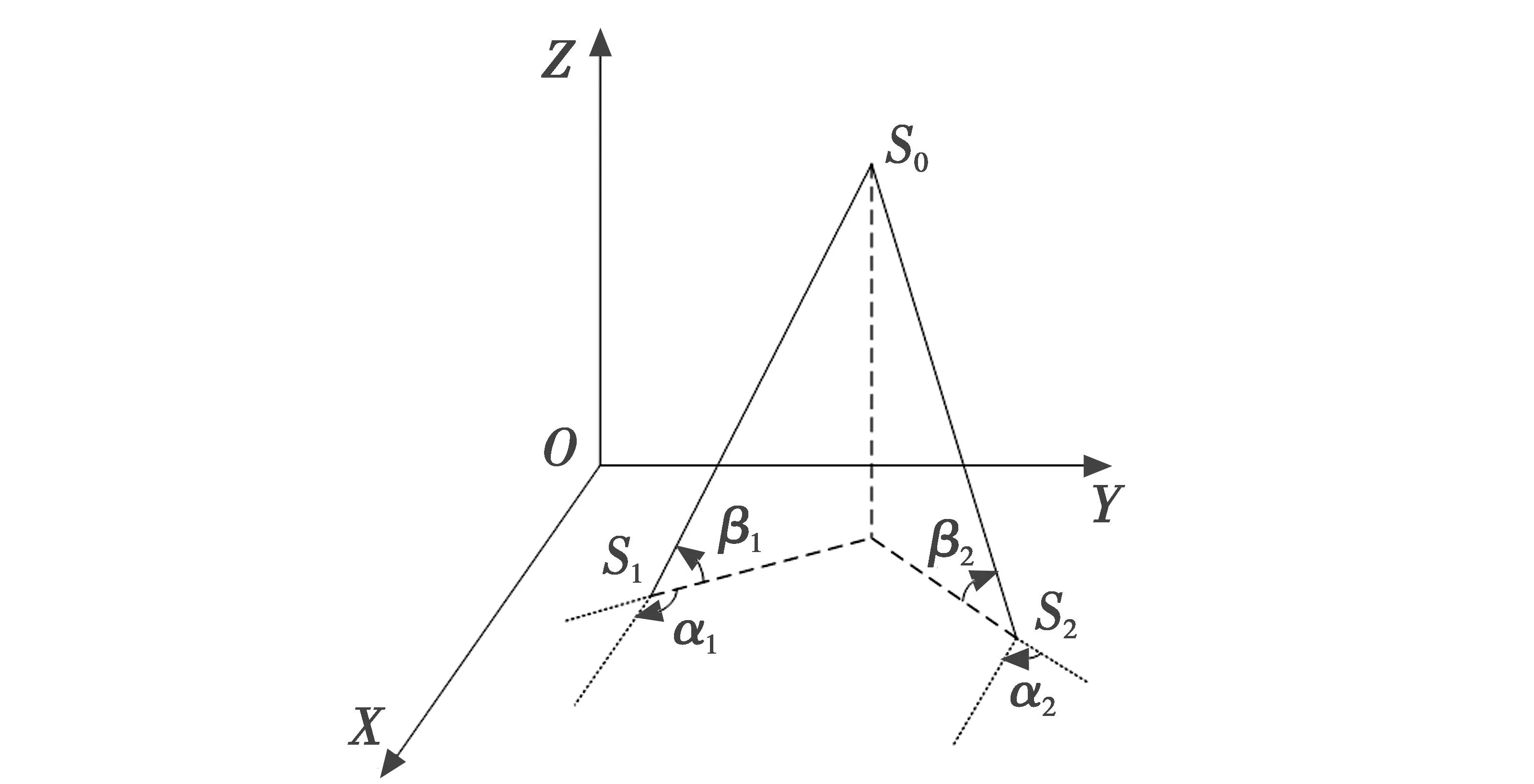
图1 双IRST测向交叉定位原理

图1中,载机1位置为S1(x1,y1,z1),载机2位置为S2(x2,y2,z2),目标位置为S0(x,y,z),S1对目标的方位俯仰角为(α1,β1),S2对目标的方位俯仰角为(α2,β2)。

以量测(α1,β1,α2)为例,根据三角关系可得

(1)

(2)

其中,d为目标到载机1的欧氏距离。

2 定位误差分析

几何精度因子(GDOP)[13-14],用于衡量测向定位精度,其大小与空间目标和各载机几何位置关系有关。GDOP越小,定位精度越高。在目标定位过程中,GDOP定义为待测目标的定位误差均方根[15]。

对式(1)两边做微分运算,可得

dS=C·dX

(3)

式中:S=[α1β1α2]T,为量测矩阵;X=[xyz]T,为目标位置矩阵;C为状态矩阵,

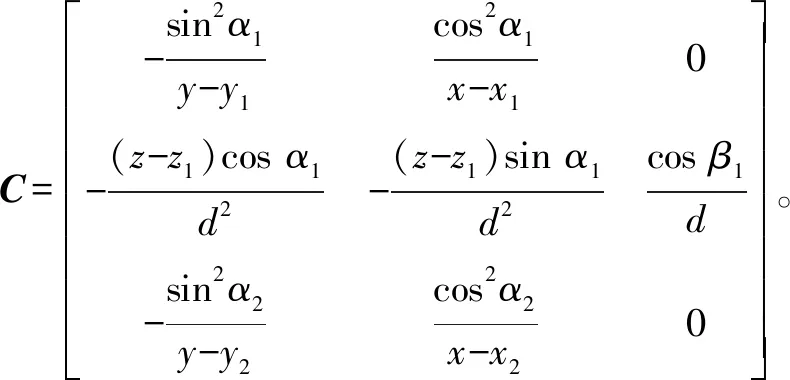
(4)

则定位误差协方差矩阵为

P=E(dX·dXT)=C-1E(dS·dST)C-T

(5)

即

(6)

则在双机协同定位中,GDOP表达式为

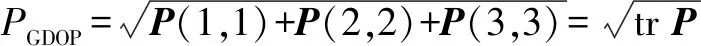
(7)

式中:P为3×3的定位误差协方差矩阵;trP为定位误差协方差矩阵的迹;P(1,1),P(2,2)和P(3,3)为定位误差协方差矩阵的对角线元素。

3 基于CS-UKF的双机协同定位模型

在双机协同定位过程中,IRST角度量测与目标位置呈非线性关系。因此,采用CS-UKF滤波算法对目标状态进行估计。

当前统计模型[16]认为目标在当前时刻以某一加速度机动时,下一时刻加速度的取值是有限的,只能在当前加速度的邻域内。非零均值加速度为

(8)

式中,w(t)为量测误差。

状态方程离散化形式为

(9)

式中各矩阵表达式见参考文献[3],当前统计模型采用修正的瑞利分布描述目标的机动加速度,更能够反映机动目标的机动范围。

量测方程(以α1,β1,α2为例)为

(10)

量测方程为非线性方程,采用UKF对目标进行状态估计。UKF是在UT变换[17]的基础上发展起来的,UT变换的基本思想是利用一组Sigma采样点来描述随机变量的高斯分布,然后通过非线性模型的映射,利用加权统计线性回归的方法来估计非线性函数的统计特性。相比于EKF,UKF无需计算雅可比矩阵,不需对非线性系统进行线性化,UKF估计精度能够精确到泰勒级数展开的二阶精度,因此,UKF在许多方面都得到了广泛应用。

UKF滤波算法概述如下。

根据初始状态估计获得2n+1个采样组合(即Sigma点集)及其权值Wi,根据状态方程可得xi的一步预测

xi(k+1|k)=f[xi(k|k),k]

(11)

式中:xi(k+1|k)为Sigma点集的一步预测,f(·)为状态方程;xi(k|k)为Sigma点集在k时刻的最优估计。

利用Sigma点集的一步预测xi(k+1|k)和权值Wi即可得到状态预测估计和状态预测协方差,即

(12)

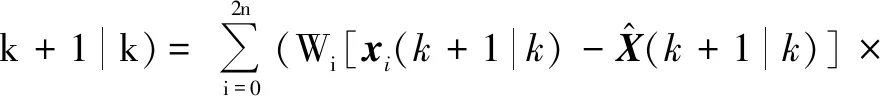
(13)

根据量测方程,可得Sigma点集的量测预测值

zi(k+1|k)=h[xi(k+1|k),k]

(14)

式中:zi(k+1|k)为Sigma点集的量测预测值;h(·)为量测方程。

则量测预测和相应的协方差分别为

(15)

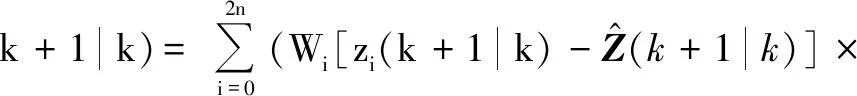
(16)

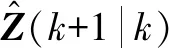
同理,可得量测和状态向量的交互协方差为

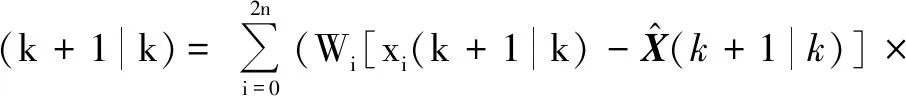
(17)

式中,Pxz(k+1|k)为量测和状态向量的交互协方差。

如果k+1时刻传感器所得量测为Z(k+1),则状态更新方程和状态更新协方差为

(18)

(19)

P(k+1|k+1)=P(k+1|k)-K(k+1)PzzK(k+1)T

(20)

4 基于自适应联邦滤波的多IRST协同定位方法

以多IRST纯角度被动定位为背景,将GDOP作为优化指标,首先对多IRST进行双机组合配对,依据GDOP值构造面向定位精度的信息类函数确定信息分配系数,结合自适应联邦滤波算法实现信息融合。

信息类函数构造如下

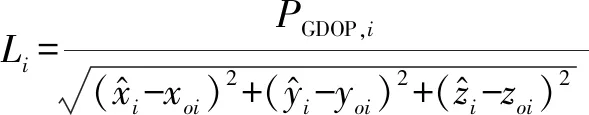
(21)

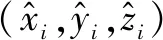
对Li进行归一化处理:

(22)

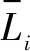
以A、B、C 三机为例,AB、AC、BC 分别构成3个双机定位子系统,各子系统基于GDOP构造面向定位精度的信息类函数,进而确定信息分配系数,最后结合自适应联邦滤波实现信息融合,得到目标全局最优估计,自适应联邦滤波如图2所示。

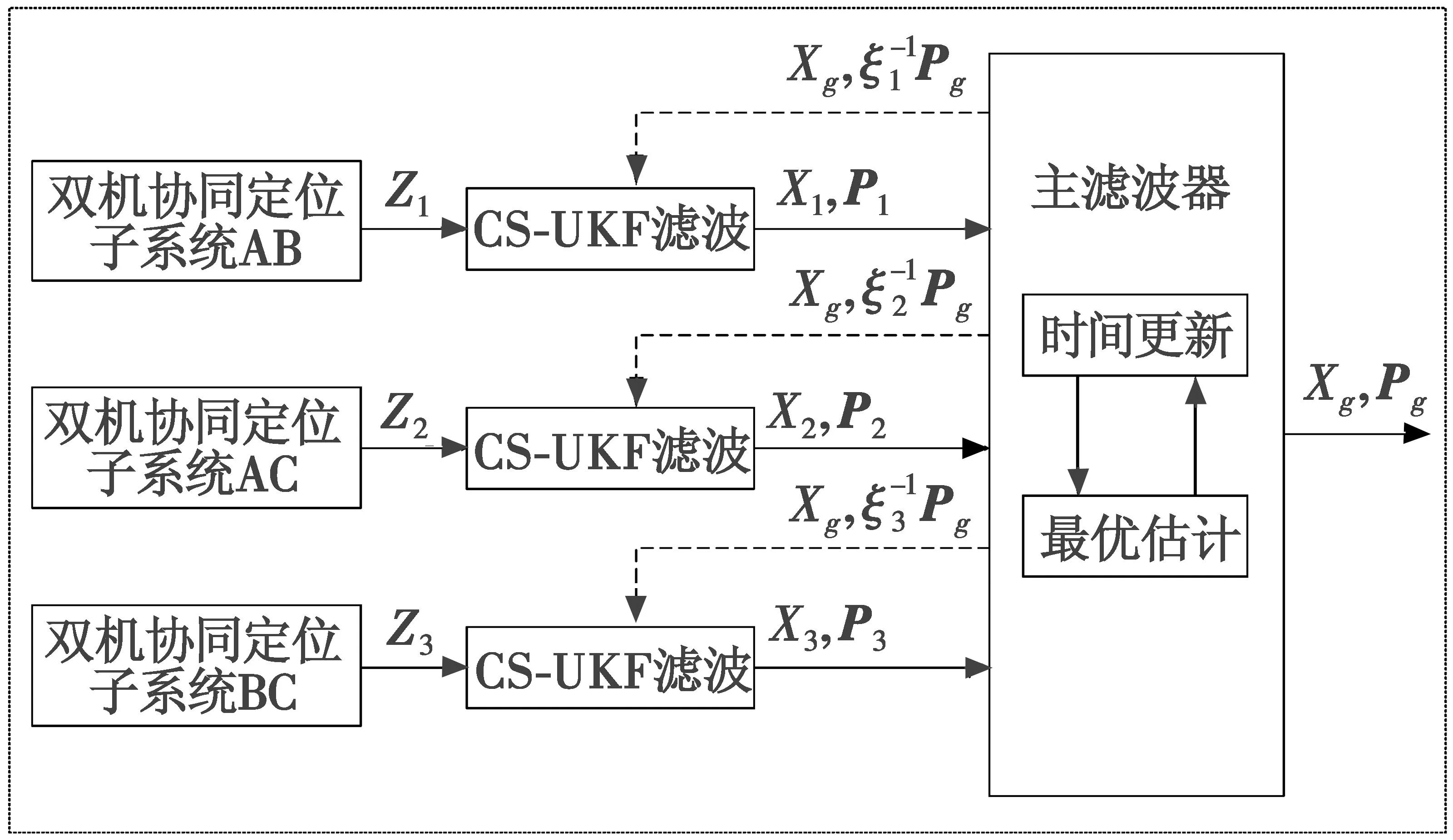
图2 自适应联邦滤波结构

自适应联邦滤波具体流程如下所述。

1) 各子系统利用CS-UKF滤波算法处理各自的量测信息,用k-1时刻的全局最优估计Xg(k-1|k-1)获得局部状态估计X1(k|k),X2(k|k),X3(k|k);用k-1时刻全局误差协方差矩阵P(k-1|k-1)获得局部误差协方差矩阵P1(k|k),P2(k|k),P3(k|k)。

2) 基于各子系统量测信息,直接进行定位解算,确定目标量测位置信息,根据量测位置信息实时计算3个双机协同定位子系统相对于目标量测信息的GDOP值,即PGDOP,i(k),i=1,2,3。

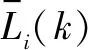
4) 依据L设计联邦滤波信息分配系数

(23)

式中:e为自然常数;ξi(k)为不同双机协同定位组合的信息分配权值。

5) 联邦滤波全局信息融合表示为

(24)

式中:P(k|k)为k时刻的全局误差协方差矩阵;Pi(k|k)为k时刻的局部误差协方差矩阵;X(k|k)为k时刻的全局状态估计;Xi(k|k)为k时刻的局部状态估计。

6) 联邦滤波信息分配表示为

(25)

式中:Q(k)为系统总过程信息;Qi(k)为各子系统局部过程信息。

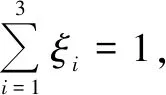
5 仿真实验验证

通过仿真对基于GDOP的多IRST自适应联邦滤波协同定位技术和传统双机协同定位信息融合技术的性能进行对比,传统双机协同定位信息融合技术为各双机协同定位组合各自进行状态估计,最后对结果进行平均融合。本文仿真设置A、B、C 3架载机对目标进行协同定位,3架载机保持匀速飞行,目标在1～60 s匀速飞行,在61～160 s螺旋上升飞行,在160～200 s继续匀速飞行。仿真参数设置如表1所示。

表1 仿真参数

目标真实运动轨迹如图3所示。

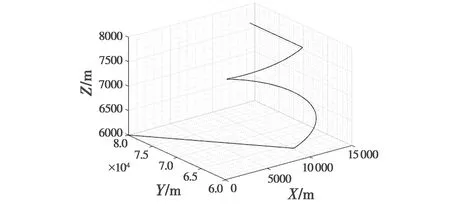
图3 目标真实运动轨迹

本文协同定位技术仿真结果如图4所示。从图4可以看出,本文协同定位技术可以很好地对目标运动轨迹实时高精度跟踪。

图4 载机与目标运动态势及跟踪情况

为对比两种协同定位技术的优劣性,对二者的三轴向坐标定位误差及距离误差进行对比分析,两种协同定位技术三向坐标误差如图5所示。

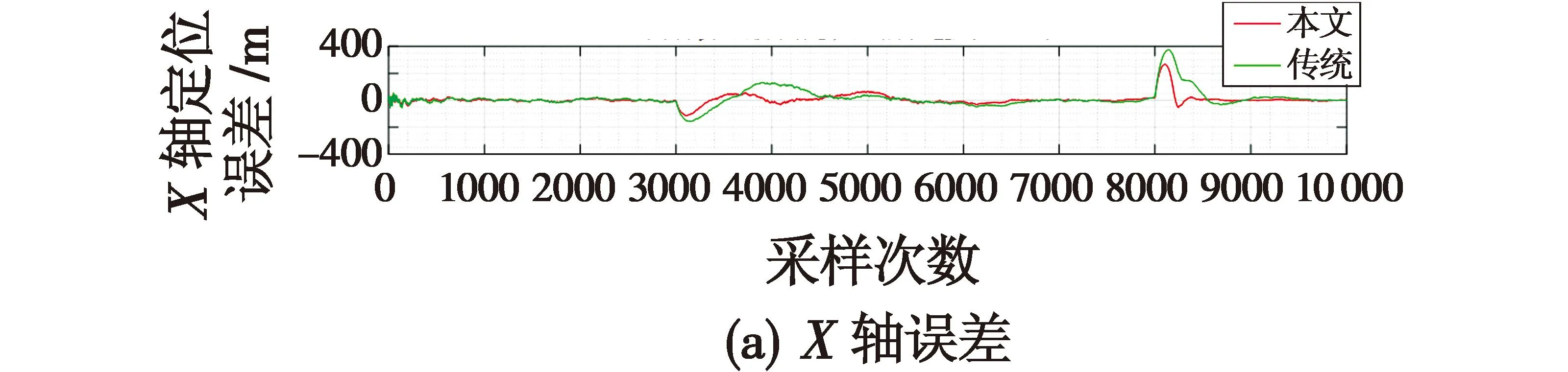
图5 两种协同定位技术三向坐标轴定位误差对比

两种协同定位技术定位距离误差如图6所示。

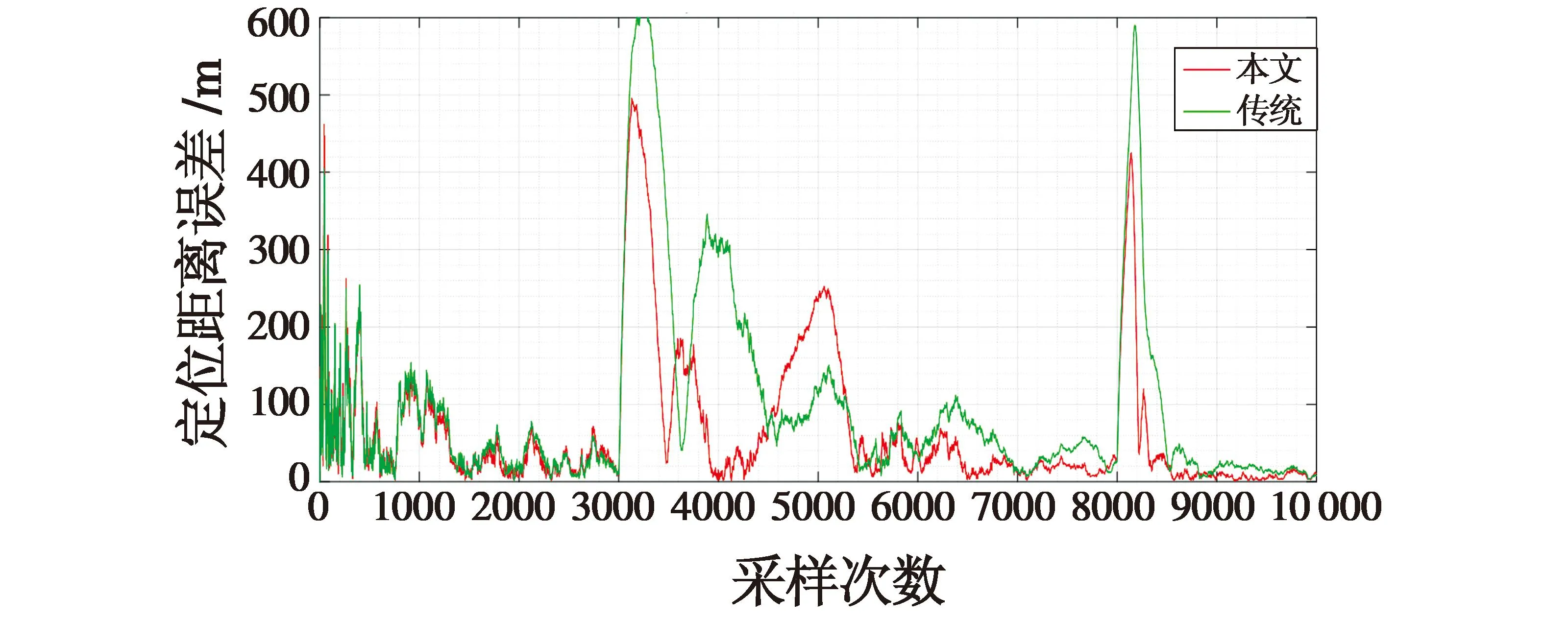
图6 两种协同定位技术定位距离误差对比

从图5、图6可以看出,本文协同定位技术的定位效果较好。经收敛后,X轴定位误差在100 m以内,Y轴定位误差在200 m以内,Z轴定位误差在50 m以内,距离定位误差在200 m以内。其中,在采样次数n=3000时定位误差突然增大,其原因为目标在n=3000时进行螺旋上升式机动,导致滤波模型需重新收敛,定位误差增大;n=8000时目标由螺旋上升式机动转为匀速直线运动,定位误差增大,需重新收敛。由图6可知,当目标发生较大机动时,本文协同定位误差波动较小,而传统双机协同定位信息融合定位误差波动较大,可证明本文协同定位技术稳定性较好。

为更直观地比较二者的优劣性,通过计算均方根误差(RMSE)来判断,RMSE是均方误差的算术平方根,用来衡量真值与预测值之间的偏差,RMSE越小,定位精度越高。RMSE算式为

(26)

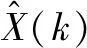
本文协同定位RMSE值较小,为98.235 4,多机协同定位效果较好,传统协同定位RMSE值较大,为157.058 2,协同定位效果较差,本文协同定位较传统协同定位精度提升40%左右。

6 结论

本文基于GDOP对多IRST协同定位技术展开研究。首先对多IRST进行双机组合配对,依据GDOP值构造面向定位精度的信息类函数确定信息分配系数,各双机组合子系统采用CS-UKF算法处理自己的量测信息,最后结合自适应联邦滤波算法实现信息融合。仿真结果表明,本文协同定位技术大大提高了定位精度,定位误差在100 m左右。在提高定位精度的同时,其信息分配原则可有效降低定位精度较差组合的估计结果对全局信息融合的影响,进而保证全局定位结果的精确性及稳定性。