一种基于线特征约束的无人机双目视觉SLAM算法
2024-04-19金凌云王从庆李宏光
金凌云, 王从庆, 李宏光
(南京航空航天大学自动化学院,南京 211000)
0 引言
同时定位与地图构建(Simultaneous Localization and Mapping,SLAM)是机器人在未知环境下进行作业的关键技术[1]。在未知环境下,机器人通过相机、IMU等传感器获取信息,SLAM算法利用获取到的信息构建所处环境地图,提供机器人的位姿信息,并随着机器人的移动实现连续地图构建与定位。根据所用传感器不同,SLAM可以分为激光SLAM和视觉SLAM。相较于激光SLAM所用的激光雷达等测距传感器,视觉SLAM所用的相机具有体积小、成本低等特点[2-3],适合用于无人机等小负载、低功耗的设备上。
目前有很多基于优化的视觉SLAM算法,其中,提取点特征的视觉SLAM算法包括ORB-SLAM系列[4-6]、VINS-Mono[7]、VINS-Fusion[8]等。ORB-SLAM[4]是一个基于特征点的实时单目SLAM系统,通过提取图像中的ORB特征实现机器人的定位与建图,并且通过改进ORB特征使其具有旋转和缩放不变性,进一步提升算法的鲁棒性;ORB-SLAM2[5]在ORB-SLAM的基础上加入了对双目相机和RGB-D相机的支持,进一步拓展了算法的应用场景;VINS-Mono是第一个前端通过LK光流[9]实现特征点跟踪和匹配的单目VIO算法,由于不需要像ORB-SLAM一样提取ORB特征,减少了前端所需时间,简化了代码;VINS-Fusion在VINS-Mono的基础上增加了对双目相机的支持,使其具有单目、双目、单目+IMU、双目+IMU 4种工作模式,其在多个数据集上的表现都十分优异。
提取点线特征的视觉SLAM算法包括PL-VIO[10]、PL-VINS[11]、PL-SLAM[12]等,其中,线特征的提取主要使用直线分割检测(Line Segment Detector,LSD)算法,并计算线带描述子(Line Band Descriptor,LBD)以便后续进行线特征匹配[13-14]。PL-VIO在VINS-Mono的基础上加入了线特征的提取及后端优化,其精度相较于VINS-Mono有所提高,但由于线特征的提取和匹配需要大量的运算,所以PL-VIO并不能够实时运行;PL-VINS通过调整OpenCV提取线特征的参数,加快了前端提取线特征的速度,使得算法能够实时运行;PL-SLAM是双目点线特征的视觉SLAM算法,其在前端、后端和回环部分均加入了线特征,进一步提高了算法的精度,并且具有实时性。
在VINS-Fusion算法中,后端考虑了双目相机观测特征点的3种情况,即单目相机在两帧下观测同一点、双目相机在两帧下观测同一点、双目相机在一帧下观测同一点,并分别计算了残差块和雅可比矩阵。为了更好地利用线特征对相机位姿进行约束,本文针对双目线特征的SLAM算法,将双目相机观测线特征分为了3种情况:只有左目相机或只有右目相机在两帧下观测到同一条线段;双目相机在两帧下观测到同一线段;双目相机在一帧下观测到同一线段。并基于上述线特征约束计算了这3种情况对应的残差块及雅可比矩阵,改进了VINS-Fusion算法并在EuRoC数据集[15]上进行了验证,结果表明本文所提算法可以在保证实时性的同时提高定位精度。
1 系统框架
点线视觉SLAM算法后端处理流程如图1所示。
对于前端提取到的点/线特征,首先进行三维重建获取深度信息,并将图像和IMU信息进行视觉惯性对齐,然后计算先验约束、预积分约束和重投影约束放入基于滑窗的非线性优化中进行优化,最后根据边缘化的是最老帧还是次新帧进行地图点/线管理。
2 线特征后端约束
2.1 空间直线的两种参数化方法
空间中一条直线有4个自由度,所以只需要4个参数就可以表示一条直线。普吕克参数化方法[16]包含6个参数,主要用于空间直线的平移与旋转,由于过参数化的问题,其不能用于无约束的优化问题。而空间直线的正交表示只需要4个参数,在优化问题时较为方便,并且2种参数化方法可以很方便地相互转化,因此在空间变换时使用Plücker坐标表示,在优化时使用正交表示 。
空间直线的普吕克坐标表示为L=(nT,dT)T∈R6,如图2所示。
图中:c为相机光心;d∈R3为直线的方向向量,n∈R3是由直线和相机光心构成的平面π的法向量。当给定世界坐标系到相机坐标系的变换矩阵Tcw,可实现普吕克坐标变换,即
(1)
式中:Lc为直线在相机坐标系下的坐标;Lw为直线在世界坐标系下的坐标;Rcw表示世界系到相机系的旋转矩阵;[·]×表示三维向量的反对称矩阵。从不同的两帧图像观测到一个新的线特征时,可用如下方法初始化线的普吕克坐标:将两帧图像的相机光心c1、c2分别与直线L确定两个平面π1和π2,这两个平面可以确定空间唯一直线。有了这两个平面可以得到对偶普吕克矩阵
(2)
从对偶矩阵中可提取普吕克坐标。
在优化时需要使用直线的正交表示(U,W)∈SO(3)×SO(2)。已知直线的普吕克坐标L=(nT,dT)T,对其进行QR分解得到

(3)
式(3)第1项为正交矩阵U,表示的是相机坐标系到直线坐标系的旋转,即

(4)
式中,ψ=[ψ1ψ2ψ3]T。由于正交矩阵U已经包含了3个自由度,所以式(3)第2项W只有1个自由度,可以利用三角函数矩阵表示为
(5)
式中,φ为旋转角。至此,正交表示的4个自由度已经求出,在优化时,使用O=[ψφ]T作为空间直线更新的最小表示。
2.2 线特征的残差模型
空间中一直线L=[nTdT]T可以通过相机内参矩阵K投影至像素平面:
(6)
式中:l1,l2,l3为直线在像素平面内的坐标;fx,fy,fz为x,y,z3个方向上的焦距;cx,cy,cz为像素坐标系的原点。而线特征的重投影误差rl定义为图像中观测线段的端点到空间重投影回像素平面的直线的距离,
(7)

为了最小化线的视觉重投影误差rl,需要计算其对于约束变量的雅可比矩阵,由链式求导法则可得
(8)
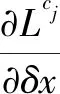
1) 单目相机在两帧下看到该线段,约束变量有第i帧IMU系的位姿Twbi、第j帧IMU系的位姿Twbj、相机外参Tbc。对上述约束变量求偏导得到雅可比矩阵为
(9)
式中:Rwbi表示左目IMU系到世界系的旋转矩阵,twbi表示左目IMU系到世界系的平移矩阵;(nbi,dbi)为左目IMU系下直线的普吕克坐标;Rwbj表示右目IMU系到世界系的旋转矩阵,twbj表示右目IMU系到世界系的平移矩阵;(nw,dw)表示直线在世界系下的普吕克坐标;Rbc表示相机到IMU的旋转矩阵,Rbjbi表示左目IMU到右目IMU的旋转矩阵,Rcjci表示左目相机到右目相机的旋转矩阵;(nci,dci)表示左目相机系下直线的普吕克坐标。
2) 双目相机在两帧下看到该线段,约束变量有第i帧IMU系的位姿Twbi,第j帧IMU系的位姿Twbj,左目相机外参Tbci,右目相机外参Tbcj,对上述约束变量求偏导得到雅可比矩阵为
(10)
式中:Rwbj表示右目IMU系到世界系的旋转矩阵;twbj表示右目IMU系到世界系的平移矩阵;(nbj,dbj)为右目IMU系下直线的普吕克坐标;Rbci表示左目相机到IMU系的旋转矩阵,tbci表示左目相机到IMU系的平移矩阵;Rbcj表示右目相机到IMU系的旋转矩阵,tbcj表示右目相机到IMU系的平移矩阵;(ncj,dcj)表示右目相机系下直线的普吕克坐标。
3) 双目相机在一帧下看到该线段,为了保持下标的一致性,此处仍用cj表示右目相机在同一帧下的观测。约束变量有左目相机外参Tbci,右目相机外参Tbcj,由于同一帧下IMU系并不发生变化,所以有Lbi=Lbj。对上述约束变量求偏导得到雅可比矩阵为
(11)
上述双目相机观测线段的3种情况如图3所示。

图3 双目相机观测线段
3 实验与分析
利用Ceres-solver的解析求导功能,将上文计算出的残差及雅可比矩阵填入定义好的矩阵块中,并基于此改进VINS-Fusion算法后端的非线性优化部分。实验的运行环境为Ubuntu18.04和ROS Melodic,CPU为i7-12700F@2.1 GHz,内存大小为32 GiB。在EuRoC公开数据集上验证所提算法并与VINS-Fusion算法进行比较,评价指标为绝对轨迹误差(Absolute Trajectory Error,ATE)、相对位姿误差(Relative Pose Error,RPE)。
3.1 EuRoC数据集及实验结果
EuRoC数据集为微型飞行器(Micro Aerial Vehicle,MAV)上收集的视觉惯性数据集,包含MH_01-05、V1_01-03、V2_01-03等11组数据,每组数据都包含双目图像和IMU信息,用于SLAM算法的输入,同时包含姿态和位置的真值信息,用于后续的指标评估。将本文算法与VINS-Fusion算法在数据集上运行,得到的轨迹误差热力图如图4所示(图中仅展示11组数据中的3组)。

图4 三维轨迹误差热力图
将运行得到的位姿数据与序列真值进行比较,实现绝对轨迹误差和相对位姿误差的计算。两种算法在EuRoC数据集上的运行结果如表1、表2所示,表中加粗数值为位姿数据最优值。

表1 绝对轨迹误差对比

表2 相对位姿误差对比
由表中数据可知,本文算法在ATE上的精度提升最大为24.3%(V1_03),最小为1.7%(V2_02);在RPE上的精度提升最大为45.5%(MH_03),最小为0.5%(MH_01),整体相较于VINS-Fusion算法精度平均提升13.2%。
3.2 实时性评估
为了验证本文所提算法的实时性,选取后端非线性优化所需时间和系统整体运行所需时间作为评价指标,结果如表3所示。

表3 非线性优化及系统整体运行耗时对比
可以看出,本文算法在运行EuRoC数据集时平均每帧非线性优化耗时37 ms,整体系统运行耗时97 ms,即平均每秒可处理10帧,可以满足实时性要求。
4 结束语
本文针对低纹理环境下的无人机双目视觉SLAM算法提出了一种新的线特征约束方法,可在特征点较少的情况下通过线特征的提取和约束仍然具有较高的定位精度和实时性。所得结果表明,本文所提算法相较于双目点特征和单目点线特征的视觉SLAM算法在低纹理环境下具有更高的精度,同时实时性也得到了保证。在后续工作中,可以进一步发挥线特征的约束作用,尝试将线特征加入回环检测中,进一步提升SLAM系统的精度。
