攻击角约束的任意时间三维制导律设计
2024-04-19丁圣巧高计委臧绍飞马建伟
丁圣巧, 高计委, 臧绍飞, 马建伟, 王 鳞
(河南科技大学,河南 洛阳 471000)
0 引言
当前,随着战场环境日益复杂、航空航天技术的快速发展,导弹或无人飞行器等机动目标在速度和变向等性能方面获得了极大的提升,这对无人飞行目标的拦截技术提出了巨大考验。制导律的设计可对上述问题的解决提供有效帮助。其中,比例导引(PN)法及其变体[1]因其形式简单而被广泛应用于制导律的设计,但在实际战争环境下,存在大量的不确定因素,致使基于比例导引法的制导律难以满足当前战争的任务需求。基于滑模控制的制导律对外界干扰和参数摄动具有较强的鲁棒性,因此受到学者的广泛关注[2]。
在拦截过程中,拦截弹与目标速度较快,系统需要在规定时间内稳定,因此,基于有限时间稳定性理论[3]的滑模制导律得到了广泛关注。文献[4]使用有限时间稳定性理论设计平面和三维制导律,给出了视线角误差有限时间收敛的充分条件和收敛时间上界的计算方式;针对机动目标拦截末制导问题,文献[5]提出一种考虑终端角度约束的自适应积分滑模制导律,能够提高拦截弹的毁伤能力;文献[6]在制导律设计中加入了自适应项,设计了自适应有限时间三维制导律,消除了目标信息带来的不确定性,并使用连续的趋近律削弱抖振现象。
有限时间制导律可以保证系统在较短时间内收敛,但收敛时间与系统的初始状态有关,这在一定程度上限制了其使用场景。针对此问题,文献[7]设计了一种非奇异终端滑模,并证明了系统收敛时间只与设置的参数有关;文献[8]基于固定时间稳定性理论设计了一种自适应固定时间非奇异终端滑模制导律,其具有更快的收敛速度,可从任意初始航向角拦截机动目标;考虑横向加速度饱和的限制,文献[9]设计了一种抗饱和自适应固定时间制导律,保证视线角误差在规定时间内收敛并保持。
固定时间制导律的收敛时间上界估计虽然只与设计的参数有关,但其调节仍较为复杂且计算出的收敛时间上界误差较大。文献[10]在固定时间的基础上,提出了一种任意时间收敛的控制器,其收敛时间可以直接由一个参数设定,避免了复杂的调参过程,并给出了任意时间收敛的证明方法;文献[11]基于任意时间稳定理论设计了一种分段滑模控制方法,并将其拓展到高阶系统中。
目前,在制导律方面的研究主要集中在固定时间方面及其相关问题上,关于任意时间收敛的制导律研究成果较少,因此本文将任意时间稳定性理论和分段滑模应用于制导律的设计,该制导律下的视线角误差收敛时间可以直接设定,无需通过复杂的计算求解。
1 系统模型及相关引理
1.1 三维弹目模型
导弹拦截机动目标的三维模型如图1所示。其中:OM-XIYIZI为惯性坐标系;OM-XMYMZM为拦截弹的速度坐标系;OT-XTYTZT为目标的速度坐标系;R代表拦截弹与目标之间的相对距离;Vm,Vt分别代表拦截弹和目标的速度矢量;θL,φL为拦截弹与目标之间的视线角;θm,φm为拦截弹速度相对于视线坐标系的方向角;θt,φt为目标速度相对于视线坐标系的方向角。
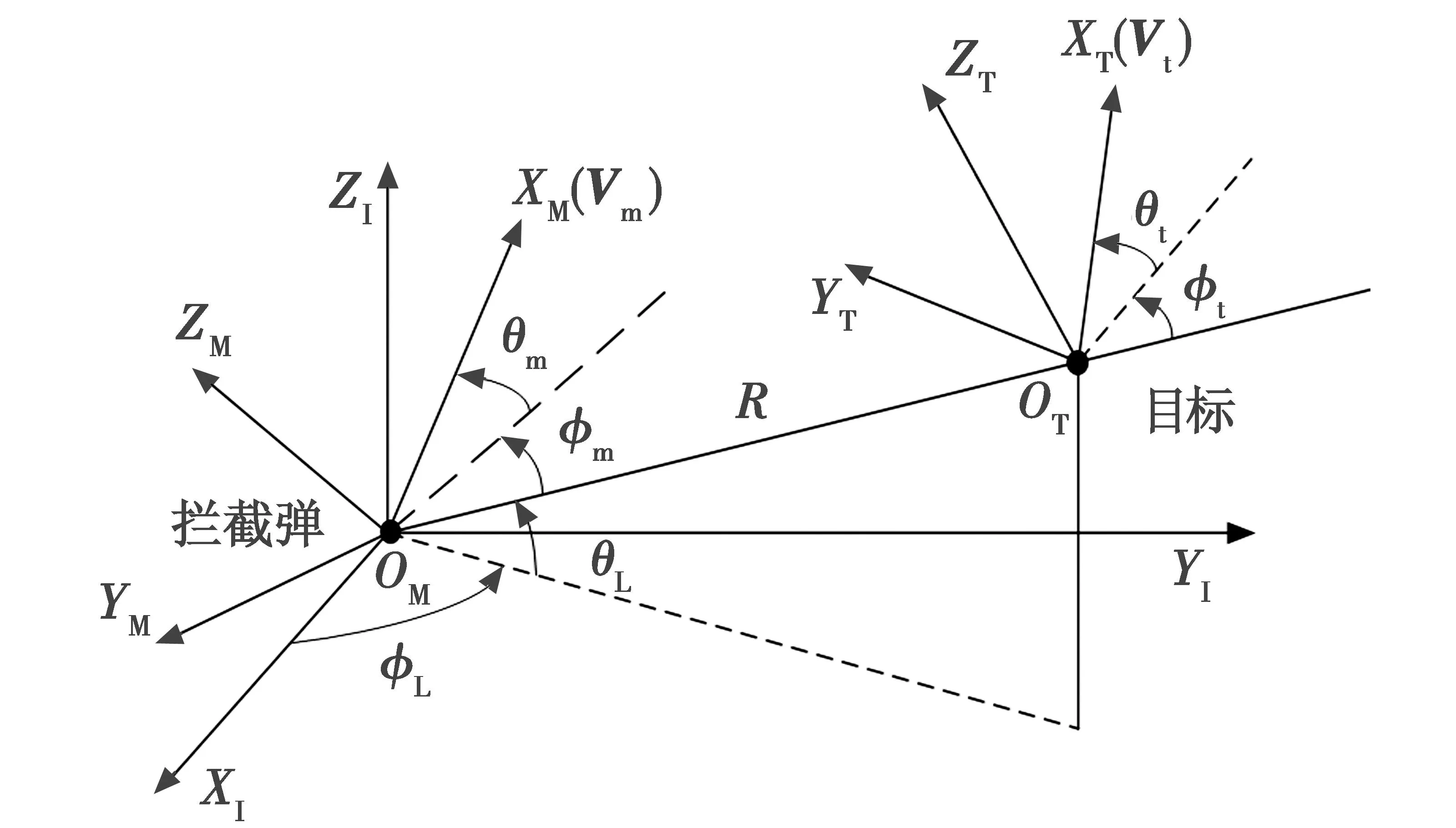
图1 三维拦截模型
基于三维拦截模型可以得出如下导弹攻击机动目标动力学方程
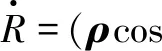
(1)
(2)
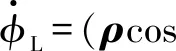
(3)
(4)
(5)
(6)
(7)
其中:aym,ayt分别为拦截弹和目标的俯仰加速度;azm,azt分别为拦截弹和目标的偏转加速度;ρ=Vt/Vm,为中间变量。
将拦截弹与目标之间的视线角θL,φL关于时间t进行二次微分,把动力学方程式(1)~(7)代入可得其二阶导数分别为
(8)

(9)
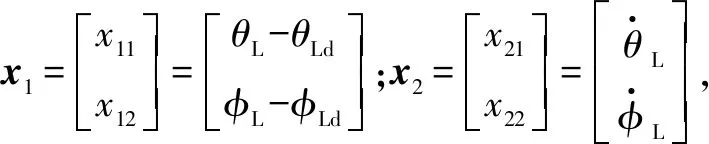
(10)
其中:θLd,φLd为期望的视线角;
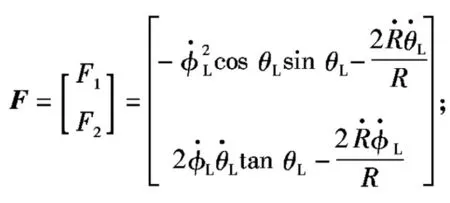
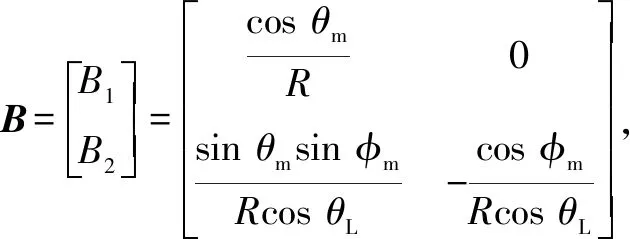
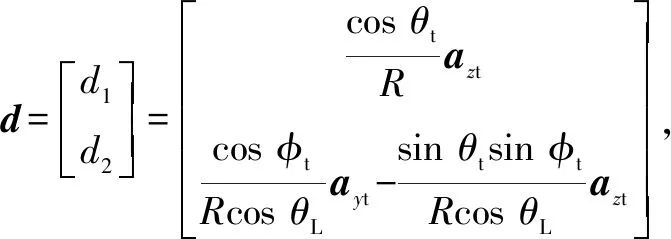
1.2 相关定义及引理
考虑如下具有时变动力学的非线性系统
(11)
式中:x∈Rn,为系统状态;ϑ∈Rp,为系统参数;f:R+∪{0}×Rn→Rn,是一个非自治的非线性函数;原点x=0是系统式(11)的平衡位置,t0∈R+∪{0}是初始时间。
引理1[12]假设存在一个连续径向无界的正定函数V(t,x)满足
(12)
那么系统式(11)就是固定时间稳定的,并且收敛时间上界可估计为
(13)
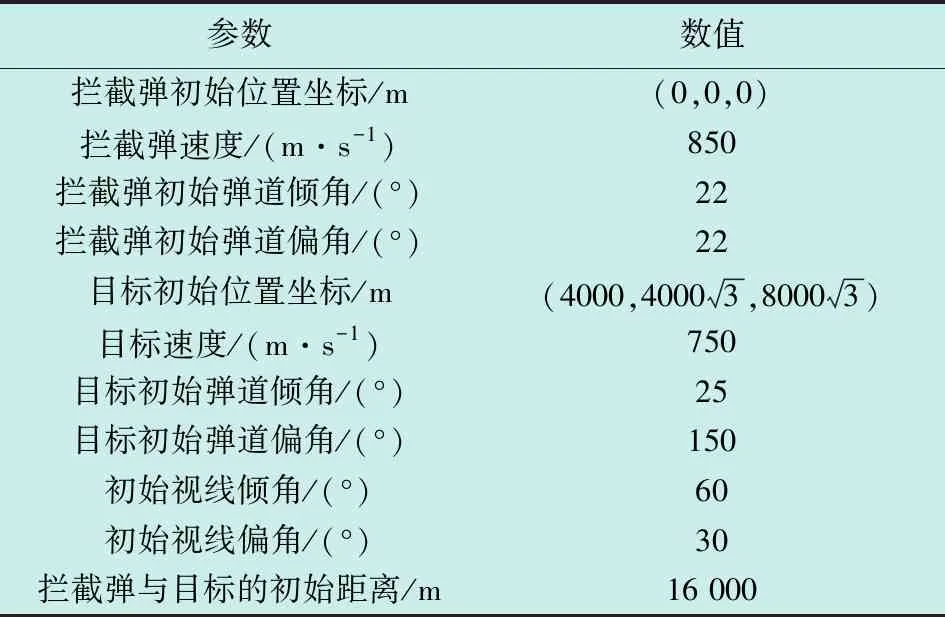
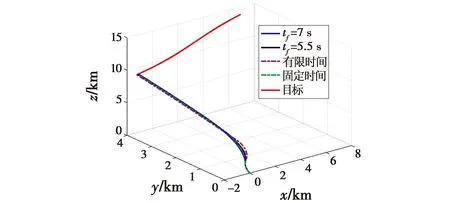
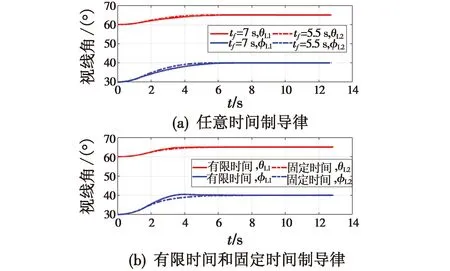
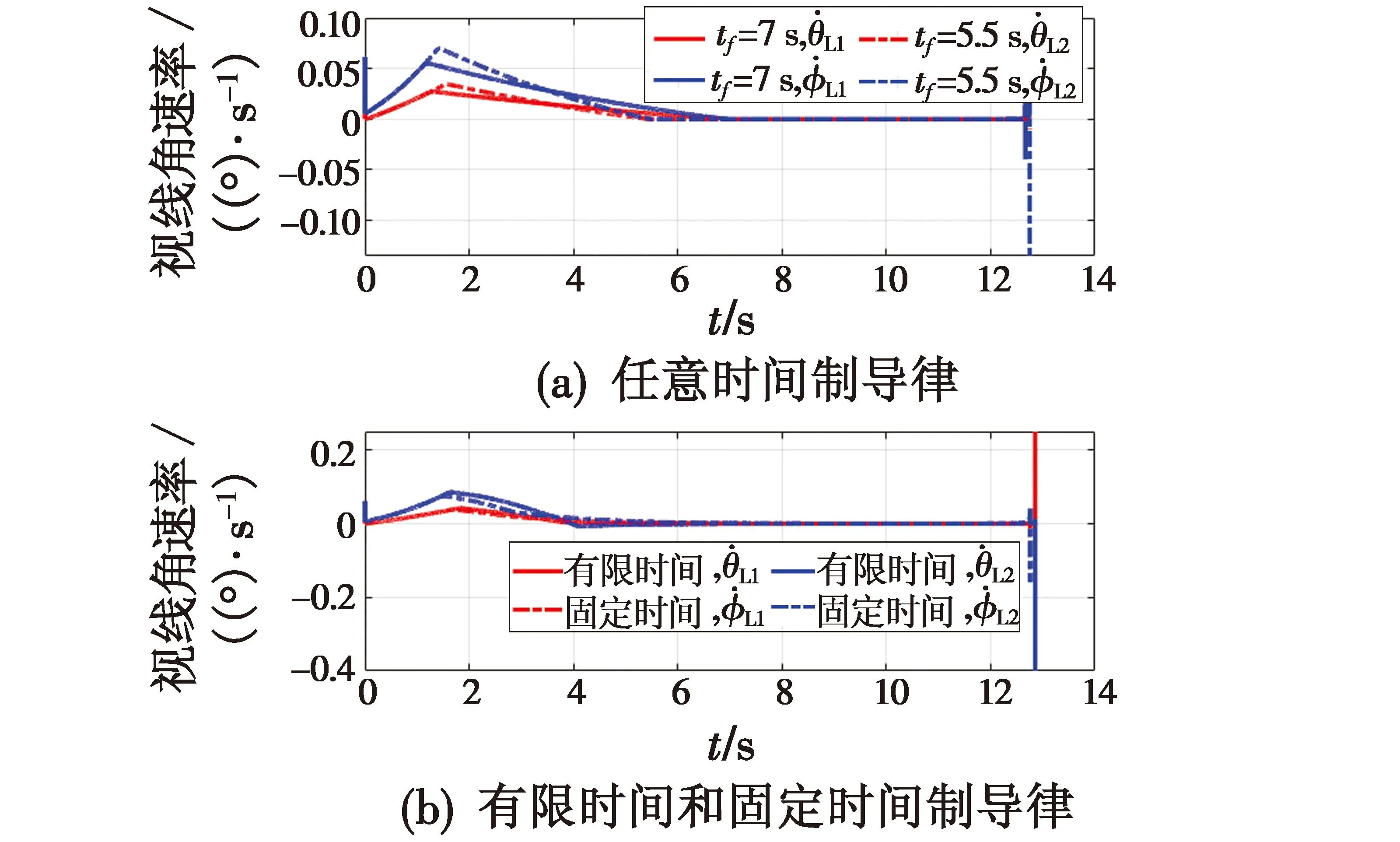
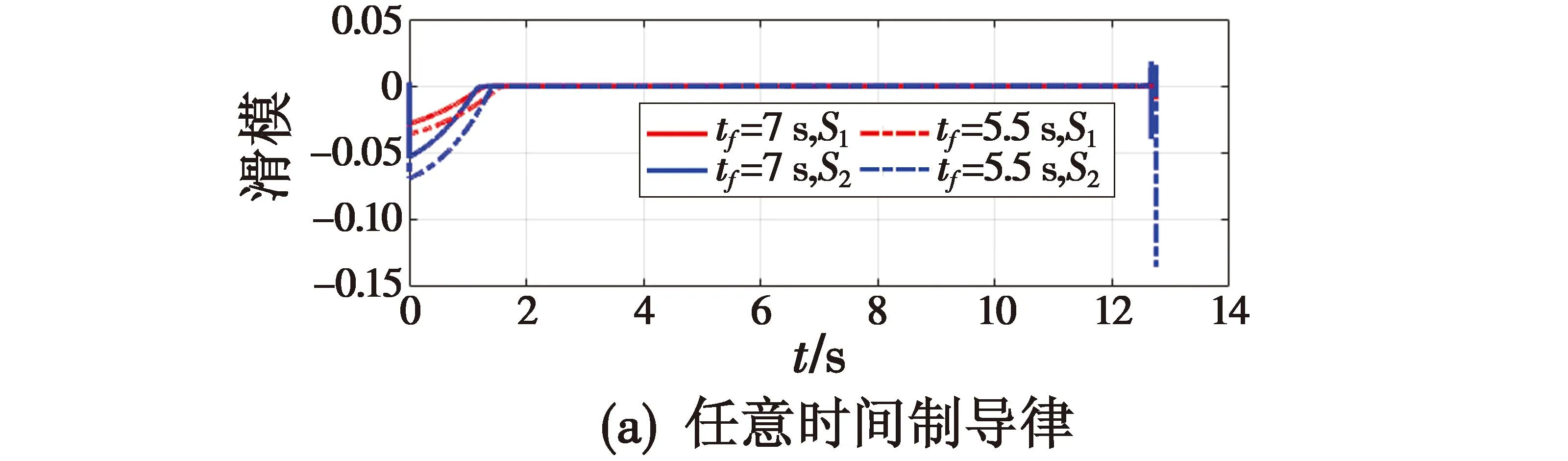
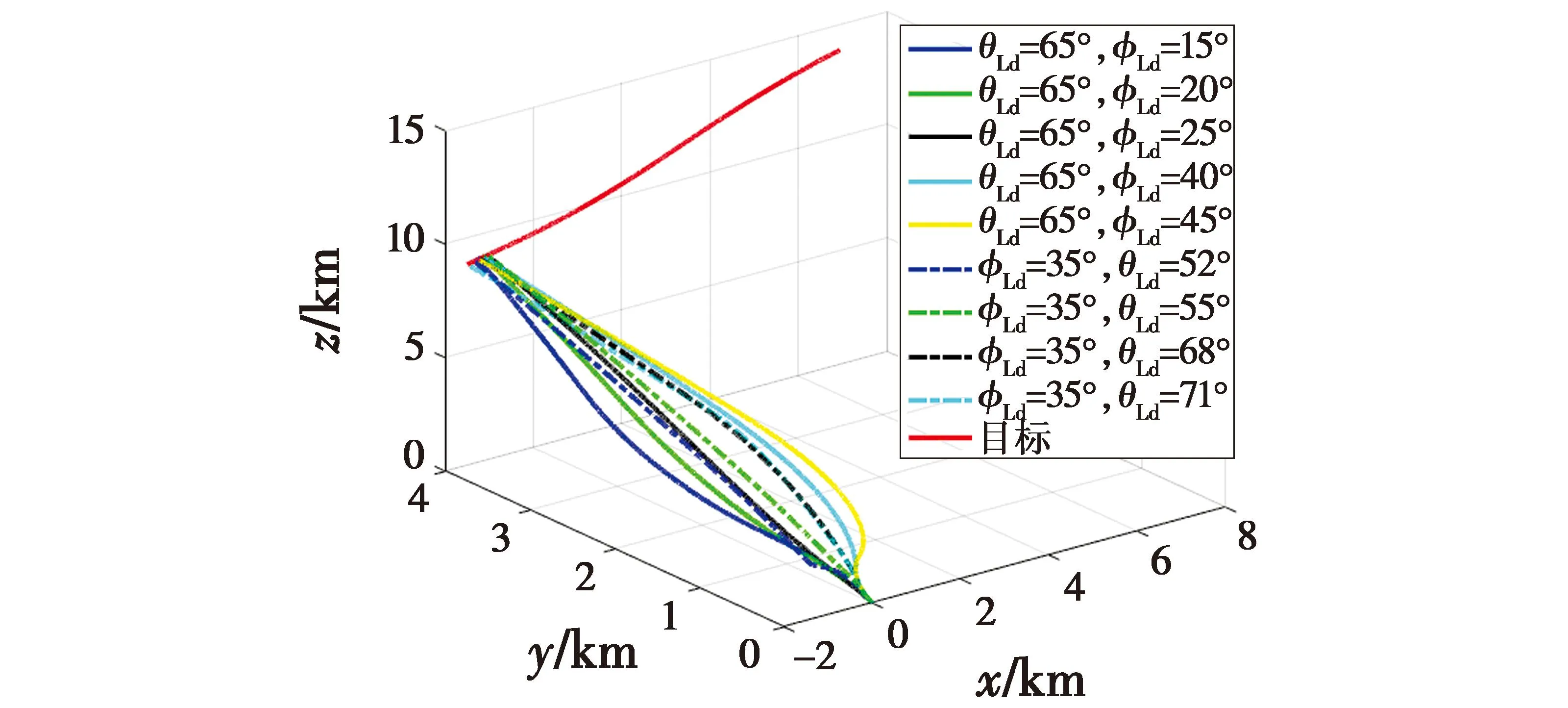
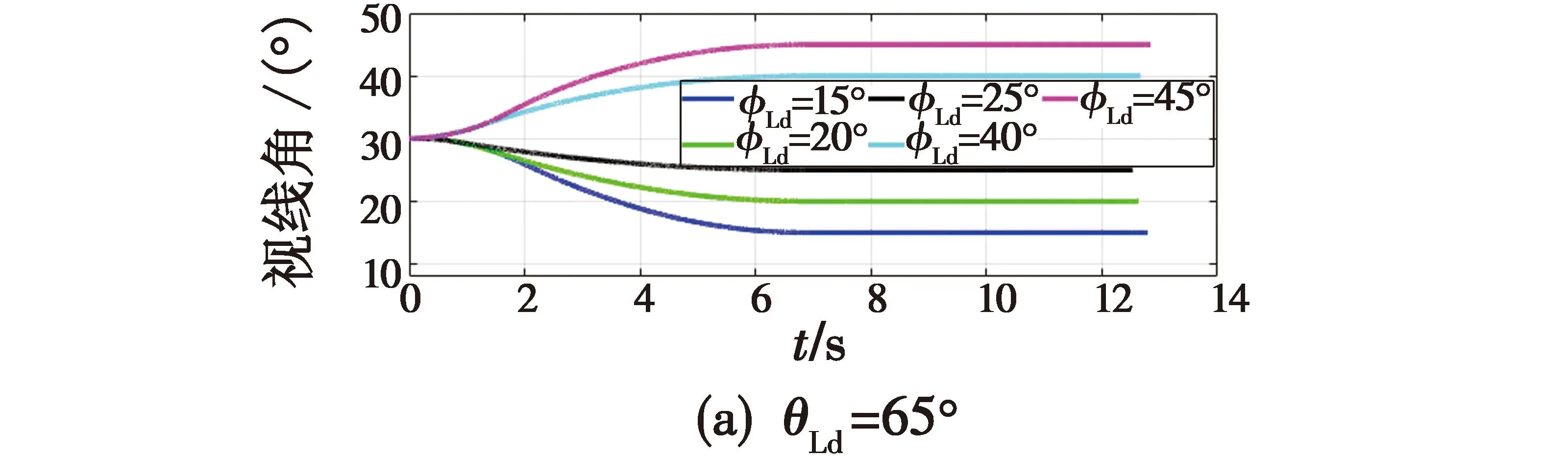
其中,参数α>0,β>0,p>1,0 定义1[10]当以下条件满足时,式(11)系统是Free-will任意时间稳定的。 1) 式(11)系统是固定时间稳定的。 2) ∃Ta>0,Ta与系统参数ϑ无关且可以被提前设定。 3) 对任何给定的ϑ,都能够建立以下任何一项 ①Ta>TesFree-will弱任意时间稳定; ②Ta=TesFree-will强任意时间稳定。 其中,Tes是式(11)系统收敛到原点的实际收敛时间。 引理2[11]考虑式(11)系统,并假设其平衡点x=0包含在集合D∈Rn中。假设在集合D中定义两个连续正定函数β1和β2。假设存在一个实值连续可微的函数V:[t0,∞)×D→R+∪{0}。 当满足下列条件时,式(11)系统是Free-will弱任意时间稳定的,且任意收敛时间为tf。 1)β1(x)≤V(t,x)≤β2(x),∀t∈t0,∀x∈D{0}; 2)V(t,0)=0,∀t≥t0; (14) 如果不等式(14)为等式,则式(11)系统是Free-will强任意时间稳定的。 根据文献[9]选择如下滑模面 (15) 当t0≤t (16) 当t≥tf时,S=k1x1+x2,对其进行微分 (17) 据此设计制导律如下 (18) 定理1若外部扰动是有界的,即|di|≤di0,且h3≥di0,采用式(18)作为制导律,则式(10)系统是任意时间收敛的,收敛时间tes≤tf。当t≥tf时,式(10)系统仍是稳定的。 证明: -h1STsigα1(S)-h2STsigα2(S)-(h3STsgn(S)-STd)≤ (19) 式中,干扰项di是有界的,即|di|≤di0,di0是一个正常数,且满足h3≥di0。 由上述分析可知,滑模变量S是固定时间稳定的,滑模变量的收敛时间算式为 (20) (21) (22) 由上述分析可知,系统是任意时间稳定的,即x1能在tf时间内收敛到零。 (23) 因此,系统总是能稳定在平衡位置。 综上,当t0≤t 实际应用中的导弹,受其发动机推力和弹体结构强度等影响,其俯仰和偏转加速度具有一定的限制,因此,限制控制器的输出,使其更加符合实际的工程应用,即 (24) 式中,umax=300 m/s2。 为了削弱由符号函数不连续性带来的抖振,使用饱和函数代替符号函数,即 (25) 为了验证所设计的制导律的有效性,对其进行数值仿真验证,实验中拦截弹与目标的相关参数如表1所示。 表1 三维模型的初始参数 假设目标具有一定的机动能力,其俯仰加速度azt=12sin 0.5t,偏转加速度ayt=10sin 0.3t,选择式(18)作为制导律,其中,η1=2.15,h1=0.575,h2=0.2,h3=12,α1=0.85,α2=1.2,k1=0.6,κ=0.04。 将制导律式(18)应用于系统式(10),为了验证该制导律的有效性,分别设置不同的收敛时间tf=7 s和tf=5.5 s进行仿真验证。将设计的任意时间制导律与有限时间制导律和固定时间制导律进行对比。 选择有限时间制导律的滑模面为 σ1=x2+k11x1+k12f(x1) (26) 式中,f(x1)=[f(x11)f(x22)]。 据此设计有限时间制导律为 (27) 选择固定时间制导律的滑模面为 σ2=x2+k21sigp2(x1)+k22g(x1) (28) 式中,g(x1)=[g(x11)g(x22)]。 据此设计固定时间制导律为 (29) 所涉及参数设定为k11=k21=0.5,k12=k22=0.2,h11=0.275,h12=0.375,h13=12,h21=0.185,h22=0.375,h23=0.8,p1=0.85,p2=1.3,p3=0.7,β11=0.75,β21=0.75,β22=1.1,ε=0.01。 仿真结果如图2~6所示。 图2 拦截弹与目标轨迹图 图2为不同制导律下拦截弹与目标轨迹图。由图2可知,在式(18)任意时间制导律的指引下,拦截弹可以完成对目标的拦截;在有限时间和固定时间制导律的指引下,拦截弹也可以完成对目标的拦截。但在不同的制导律下,拦截弹的轨迹有所差别。 图3为不同制导律下视线角变化图。 图3 视线角变化图 图3(a)表明视线角分别在7 s和5.5 s前收敛到期望的角度,两种情形下,视线角收敛到期望的角度后都能继续保持在期望的角度。图3(b)表明有限时间和固定时间制导律下视线角误差都在较短时间内收敛。图4为不同制导律下的视线角速率变化图。由图可知,视线角速率变化都较平缓。 图4 视线角速率变化图 图5为滑模面变化图。由图可知,在不同滑模面下,运动点都能在较短时间内到达滑动模态区,并保持在零附近。 图5 滑模面变化图 图6为不同制导律下拦截弹的加速度变化图。 图6(a)为任意时间制导律下的拦截弹加速度变化图。由图6(a)可知,设置不同的tf,控制器输出都是先达到最大值,之后再慢慢地降低,最后在较小的范围内变化;另外,控制器输出分别于7 s和5.5 s时发生突变,这是由于滑模面发生改变而引起的;tf=7 s的控制器输出要明显优于tf=5.5 s的控制器输出。图6(b)为有限时间和固定时间制导律下的拦截弹加速度变化图,加速度都有部分时间处于最大值。 相比于有限时间和固定时间制导律,任意时间制导律下的控制器输出处于饱和阶段的时间较短,显得更加平缓。任意时间制导律的视线角误差收敛时间更容易进行控制,设定不同的tf,视线角收敛速度不同,控制器输出也不同。在合理范围内,tf越大,视线角误差收敛时间越长,控制器输出越平缓。在此仿真初始条件下,可得当tf=7 s时,视线角的期望值范围分别为θLd∈[52°,71°],φLd∈[15°,45°]。图7为不同期望值角度下的拦截弹的轨迹图。 图7 不同期望值下的轨迹图 图8(a)为θLd取值65°,φLd分别取值15°,20°,25°,40°,45°时的视线角变化图。图8(b)为φLd=35°,θLd分别取值52°,55°,68°,71°时的视线角变化图。 图8 不同期望值下视线角的变化图 针对攻击角约束的机动目标拦截问题,引入任意时间稳定性理论和分段滑模,设计了任意时间制导律,使视线角误差的收敛时间可以直接设定,从而解决了有限时间和固定时间制导律的收敛时间上界难求的问题。并通过数值仿真验证了任意时间制导律的有效性,实验结果表明,任意时间制导律可以在合理的范围内,通过调节tf改变视线角误差的收敛时间和控制器输出情况。此外,还与有限时间制导律和固定时间制导律的仿真结果进行了比较,表明任意时间制导律控制器输出要更加平稳且更易于调节。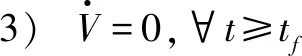

2 制导律设计及稳定性分析
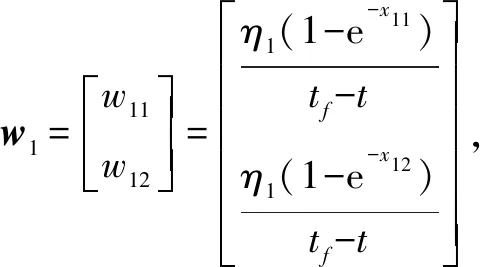

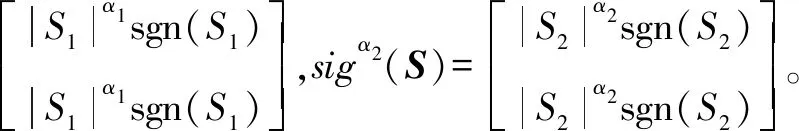
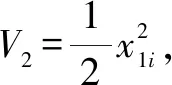
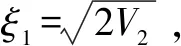
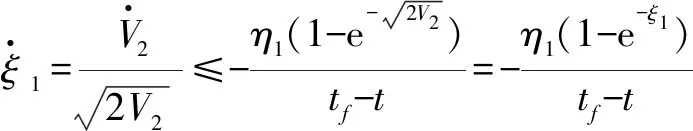
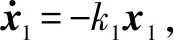
3 数值仿真
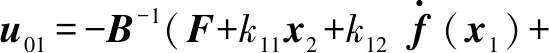
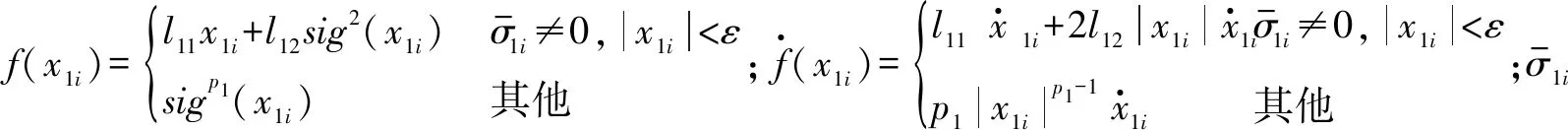
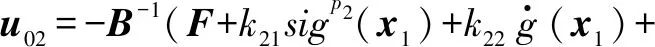
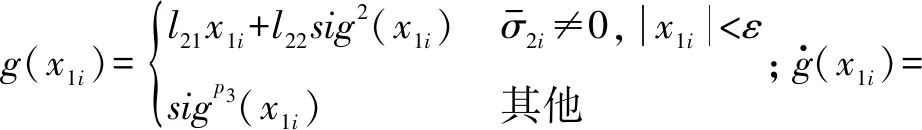
4 结论
