地铁监测测量机器人在线计量方法研究

2024-04-19马娟娟郭若成胡俊杰

计量学报 2024年3期

马娟娟, 张鑫, 郭若成, 胡俊杰

(1. 武汉地震计量检定与测量工程研究院有限公司，湖北武汉 430071；2. 中国地震局地震研究所地震大地测量重点实验室，湖北武汉 430071；3. 湖北省地震局，湖北武汉 430071)

1 引言

随着中国城市化的快速发展,地铁已成为城市交通的重要工具[1],截止到2023年,全国已有25个城市实现地铁正式运营,地铁运营总里程已超22 000公里。在地铁的施工和运营期间,周边隧道基坑工程施工、邻近项目建设施工等多种外界自然或人为因素,均会不同程度地导致地铁隧道结构发生变形,影响地铁安全运营[2～5]。因此,对地铁施工和运营期间进行周期性变形监测,成为当前确保地铁安全运营的重要工作,地铁安全监测也称为当前国家生命线重要工程。

地铁隧道变形监测常用的手段主要有传统的人工测量、基于测量机器人的监测技术、基于静力水准仪的位移监测技术、基于巴塞特收敛系统的监测技术、三维激光扫描仪自动监测技术等[6,7]。其中,测量机器人作为一种集自动目标识别、自动照准、自动目标跟踪、自动记录于一体的测量设备[8,9],可以实现对监测目标全天候不间断跟踪测量,具有监测精度高、操作灵活、受场地影响小、工作效率高等优点[10,11],成为了地铁监测的主流设备,被大量用于地铁隧道结构变形监测中[12,13],因此设备的量值准确直接决定监测结果的准确性,量值溯源也成为必须要开展的工作。

地铁监测需要连续进行,监测周期长达数年甚至数十年,监测间隔一般小于1天,测量机器人作为其主要监测设备,无法脱离工程监测线送至实验室进行溯源。同时,由于使用场景的特殊性,在监测项目中主要利用测量机器人的ATR自动识别及测量功能,而目前现行的全站仪检定规范[14,15],并没有针对该性能的相关检定方法。综上,地铁监测中测量机器人的溯源存在较大困难,因此提出了一种针对监测用测量机器人的在线计量方法,可解决其量值溯源问题,为安全监测提供技术保障。

2 ATR工作原理及特性分析

2.1 ATR工作原理

自动目标识别系统(automatic target recognition,ATR)是测量机器人所具有的一种自动识别系统[16],可实现目标(角锥棱镜)的自动搜索与识别,通过影像修正,获得目标中心的精确方向观测值(图1)。它从物镜发射红外光束,经棱镜反射回来后在CCD阵列形成光点,以CCD阵列中心作为参考确定其位置,根据图像处理算法计算得到棱镜中心,通过自动搜索,驱动望远镜接近棱镜中心,并计算出十字丝中心与图像中心的偏移量,经自动修正后,得到最终的水平角和垂直角测量值[17,18]。因此,ATR的测量能力对监测结果具有直接影响。

图1 自动目标识别系统Fig.1 Automatic target recognition system

2.2 计量特性分析

根据《城市轨道交通结构安全保护技术规范》要求,地铁运营监测中隧道水平向和垂直向位移变形速率不超过1 mm/d。测量机器人在形变监测中,主要是利用其ATR自动照准功能探测隧道的微小变化量,仪器的显示分辨力作为仪器信息的输出形式,不足以反应仪器本身的噪声水平,因此需要通过对仪器本身分辨力的测量,来反映由于仪器本身噪声水平对微小位移测量所带来的影响,即ATR的测角分辨力和测距分辨力。在监测过程中,测量机器人对空间距离的测量能力直接影响监测结果的精度,所以空间距离测量误差也是一项关键技术指标。综上,本文提出了ATR测角分辨力、测距分辨力、空间距离测量误差3个计量特性,并研究了其校准方法。

3 测量机器人在线校准方法

3.1 前期实验分析

结合测量机器人在地铁隧道中的实际监测环境,在70 m距离范围内,分别选择3、30、40、50、60和70 m左右距离位置,进行ATR测角及测距重复性实验分析,为ATR测角分辨力、测距分辨力校准距离的选择提供依据。

根据实验结果(图2和表1),在3～70 m范围内,测距重复性随距离增大没有太大变化,均优于 0.1 mm;在3 ～50 m范围内,水平角重复性、天顶距重复性随距离增大没有太大变化,均在0.1″左右,当距离增大至60和70 m时,水平角重复性、天顶距重复性明显增大。

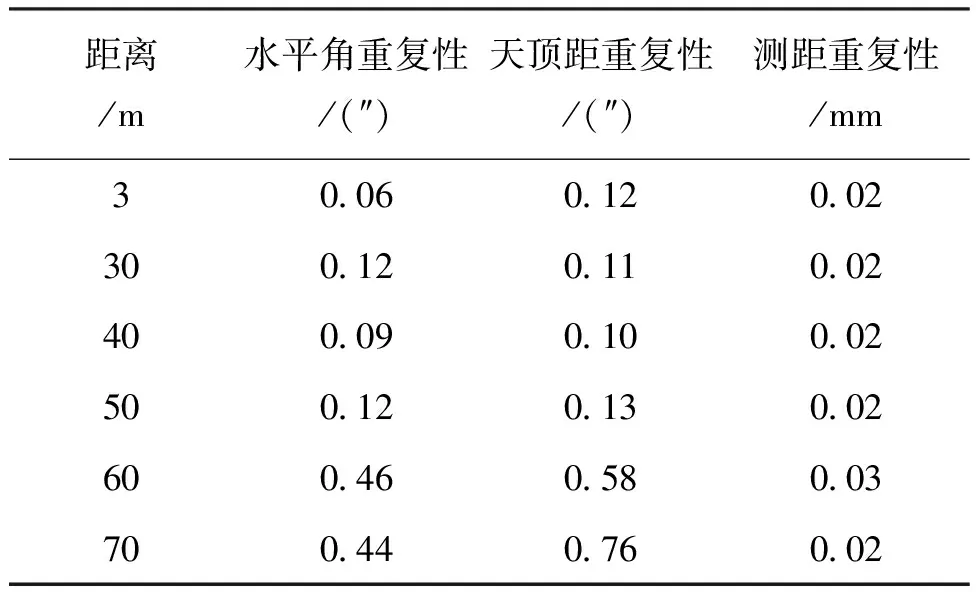
表1 重复性测量数据统计结果Tab.1 Statistical results of repeated measurements

图2 不同距离时水平角、垂直角、测距重复性Fig.2 The repeatability ofhorizontal angle,vertical angle and range at different distances

3.2 ATR测角分辨力校准

ATR测角分辨力:监测型全自动全站仪在ATR测量模式下,水平角和天顶距能够分辨的最小角度,分别用水平测角分辨力和天顶距分辨力来表征,ATR测角分辨力不大于仪器标称角度测量精度。

校准原理:由于分辨力反映的是测量机器人的角度精度,因此校准时需要可以提供水平向和垂直向微小距离的设备作为标准器。在校准过程中,只需要在一个位置安置设备,通过标准器的微小位移,进行不同角度的测量即可,无需在不同位置安置设备校准。本文利用双向分辨力检验台配合球棱镜作为标准器(见图3),分辨力检验台包括垂直向和水平向2部分位移测量装置,其示值误差最大允许误差为0.05 mm,最小分度值为0.01 mm,测量范围不小于5×10-3L(L为分辨力校准距离,单位m)。校准过程中,分辨力检验台提供标准距离值,根据仪器天顶距测量值换算为标准角度值,与ATR测量的角度值进行比较,计算其合并样本偏差,来判断ATR的测角分辨能力。

图3 分辨力检验台Fig.3 The resolution test stand

ATR水平角校准方法:经第3.1节实验验证,在 30～50 m范围内,ATR测角精度与距离关系不大,考虑到地铁隧道内现场校准环境条件的复杂性,校准方法中选择不小于30 m距离进行校准。在距测量机器人不小于30 m处安置分辨力检验台,使检验台移动的方向水平且与仪器的光轴垂直。将仪器大致照准棱镜中心,由检验台的零点位置开始,等间距移动反射棱镜10次,每次移动间隔为0.5 mm,测量机器人沿着角度增大的方向,在每个位置利用ATR测量模式进行测量,记录测量机器人的水平角βi、天顶距Zi与斜距值Si(详见图4)。

图4 测量过程示意图Fig.4 Schematic diagram of measuring process

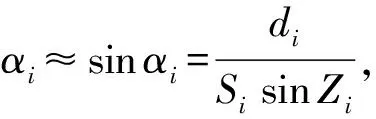
记测量机器人起始水平角为β0,每个测量位置的测量误差为ei,则有βi-αi=β0+ei。令Δi=βi-αi,根据最小二乘估计原理:

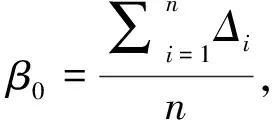
则ATR水平测角分辨力:

(1)

同理,采用分辨力检验台垂直方向,进行ATR水平角分辨力的校准。

球棱镜在垂直方向上变化的高度hi=LcotZi,则:

令

其中,n=11。

经过整理后,可以得到ATR垂直测角分辨力的计算式如下:

(2)

3.3 测距分辨力校准

在进行测距分辨力校准时,为了减少角度带来的影响,选择将检验台移动的方向水平朝向测量机器人方向,校准的过程保持同角度分辨力。以棱镜移动的距离di为标准距离,测量机器人的平距值为测量值,得到测距分辨力:

(3)

3.4 空间距离测量误差校准

测量器机人的坐标分辨力较低,而测角、测距精度较高,因此通过采用角度、距离值进行换算,计算得到空间距离值,并对距离值进行精度评定。校准过程中采用长度经过校准的长度标尺配合球棱镜作为标准器,根据三维坐标进行计算。长度标尺主体为一根铟钢棒(或碳钢棒),其2端安装磁性靶座,靶座上放置2个空心球棱镜,共同构成标准器。要求长度不小于2 m,不确定度U=0.05 mm (k=2)。选用2 m铟钢棒配合球棱镜进行空间距离测量误差的校准。

根据图5几何关系,可得A、B球棱镜的空间距离为:

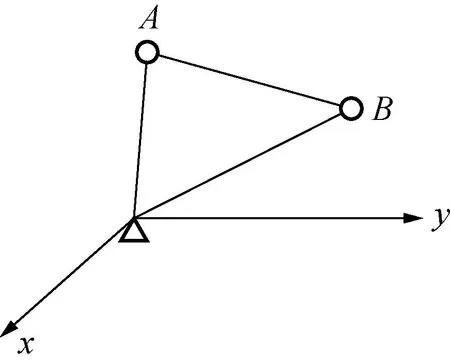
图5 棱镜三维坐标Fig.5 Three-dimensional coordinates of a prism

(4)

影响量分析:

cosZA·cosZB]}

(5)

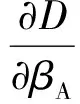
(6)

βA)-sinZA·cosZB]

(7)

空间距离测量误差校准中,在近距离处反映设备的测距加常数指标,在远距离处反映设备的测角和测距精度。根据第3.1节实验分析结果,结合长度标尺2 m的长度值能反映的角度范围,以及地铁隧道内现场校准环境条件的限制,选择近距离2 m和远距离30 m进行分析。

根据影响量分析式,对2 m水平横向、30 m水平横向、纵向、垂直向4个位置放置标准器的情况进行分析,结果如表2所示。

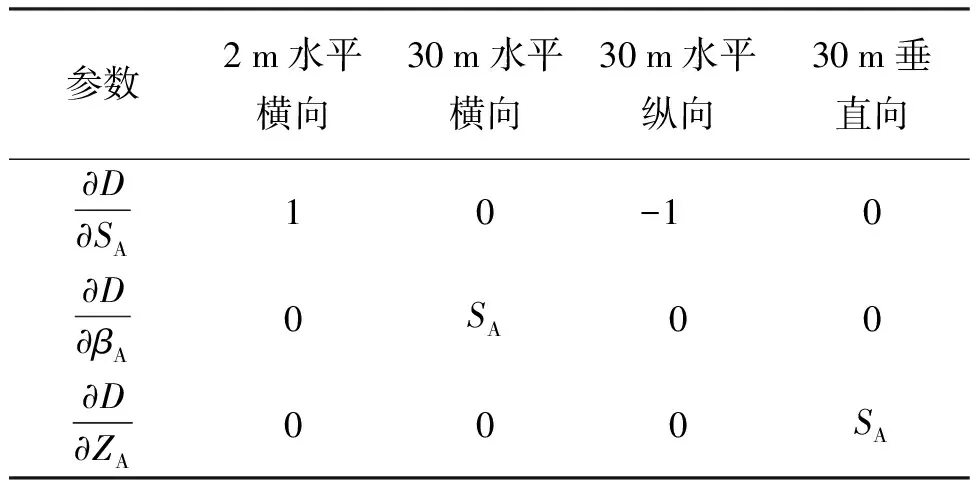
表2 空间距离测量误差校准影响量分析Tab.2 Error calibration influence analysis of space distance measurement

由表2分析可知,在2 m水平横向位置和30 m水平纵向位置处,空间距离校准结果受测距精度影响较大;在30 m水平横向处,空间距离校准结果受水平角测角精度影响较大;在30 m垂直向位置处,空间距离校准结果受天顶距测角精度影响较大。

根据以上分析结果,空间距离测量误差的校准采用以下方式:选择近距离2 m和远距离30 m处分别进行空间距离测量误差的校准(见图6);在距测量机器人2 m处,水平横向安置长度标尺,反映空间距离的加常数影响;在距测量机器人30 m处,水平横向、垂直向、水平纵向分别安置长度标尺,反映空间距离的水平角、天顶距、测距精度影响,测量过程中记录测量机器人的水平角、天顶距和斜距值;最后按照式(8)计算空间距离测量误差Δi为:

图6 空间距离测量误差校准Fig.6 Space distance measurement error calibration

Δi=Di-D

(8)

式中:Di为测量机器人测量的两棱镜在第i个位置的空间距离;D为两棱镜的空间距离标准值。

4 不确定度分析

根据校准方法,对ATR测角分辨力、空间距离测量误差的不确定度进行分析。

4.1 空间距离测量误差测量不确定度评定

采用2 m碳素钢材料长度标尺作为标准器,在距离机器人30 m处,现场温度为30 ℃的条件下,按照所提校准方法,对水平横向空间距离进行校准。测量模型为:

ΔD=D-Ds·(1+α·Δt)

(9)

式中:ΔD为空间距离测量误差;D为监测型测量机器人空间距离测量值;Ds为空间距离标准值;α为长度标尺线膨胀系数;Δt为长度标尺标定温度与校准过程中的温度差。

uc=[u2(D)+c2(Ds)u2(Ds)+c2(α)u2(α)

+c2(Δt)u2(Δt)]1/2

(10)

各个不确定度分量评定如下:

1) 测量机器人引入的不确定度

在距离机器人30 m位置处安置长度标尺,采用ATR测量模式,分别照准2个棱镜,重复测量10次,计算重复性标准偏差:

测距重复性引入的标准不确定度:

u1(D)=S(D)=0.10 mm

机器人距离显示分辨力为0.1 mm,其半宽为0.05 mm,按均匀分布估计,其引入的不确定:

重复性引入的不确定度大于分辨力引入的不确定度,取重复性引入的不确定度:

u(D)=u1(D)=0.10 mm

2) 长度标尺示值误差引入的不确定度

长度标尺的扩展不确定度U=0.05 mm,k=2,则:

校准过程中长度标尺的温度与其标定温度差值Δt取10 ℃,则:

c(Ds)u(Ds)=-0.025 mm

3) 长度标尺线膨胀系数引入不确定度

碳钢线膨胀系数为(12.0±2)×10-6K-1,最大允许误差为2×10-6K-1,假设服从均匀分布,区间半宽为2×10-6K-1,则标准不确定度为:

4) 长度标尺温度测量引入不确定度

采用最大允许误差为±1 ℃的表面温度计,对长度标尺进行温度测量,假设服从均匀分布,区间半宽为1 ℃,则表面温度计引入的标准不确定度:

c(α)u(Δt)=-Ds·α·u(Δt)=-0.014 mm

5) 合成标准不确定度uc

uc=0.11 mm

6) 扩展不确定度

U=k·uc=0.22 mm,k=2

4.2 ATR水平测角分辨力测量不确定度评定

在距离测量机器人30 m处,按照所提的校准方法,利用分辨力检验台(测量范围为20 cm,MPE:±0.05 mm)作为标准器,对测量机器人ATR水平测角分辨力进行校准。由于测量模型呈现明显的非线性特征,因此采用蒙特卡洛法(MCM)评定校准结果的不确定度。测量模型为:

(11)

式中:Si为测量机器人第i次测量的斜距值;Zi为测量机器人第i次测量的天顶距值;βi为测量机器人第i次测量的水平角度;di为分辨力检验台第i次移动的相对于起始点的距离。

各个不确定度分量评定如下:

1) 测量机器人测量重复性引入不确定度

根据重复性实验得到,测量机器人ATR测角重复性与测距重复性分别为:sH=0.433″、sV=0.266″、sD=0.042 mm,在每个位置利用ATR测量模式测量5次取平均,均服从正态分布。

2) 测量机器人显示分辨力引入不确定度

测量机器人测角显示分辨力为0.1″,其半宽为0.05″;测距显示分辨力为0.1 mm,其半宽为 0.05 mm,二者都服从均匀分布。

3) 分辨力检验台示值误差引入不确定度

分辨力检验台示值误差最大允许误差为 0.05 mm,假设服从均匀分布。

4) 蒙特卡洛试验数

样本试验数M的取值为106。

5) 计算模型值

① 假设测量机器人在进行ATR水平测角分辨力测量时,测量机器人与分辨力检验台高差为 0.5 m,且测量机器人位于分辨力检验台的对称轴平面上,以测量机器人为原点,建立测量坐标系,如图7所示。

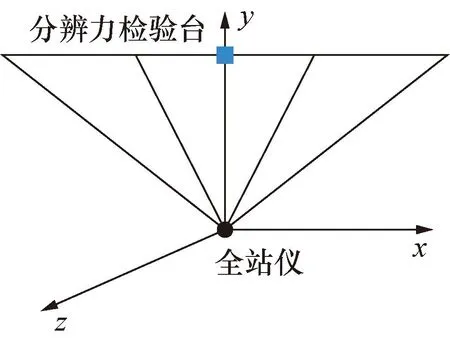
图7 分辨力测量坐标系示意图Fig.7 Schematic of resolution measurement coordinate

观测点坐标可表示为(单位mm):

记测量机器人起始水平角为β0,则测量机器人天顶距Zi、斜距值Si、水平角度βi分别为:

(12)

(13)

(14)

② 根据实验知,测量机器人ATR水平与垂直测角分辨力误差的标准差δH=0.5″、δV=0.5″,测距分辨力δD=0.032 mm,均服从正态分布。

随机生成服从上述分布的分辨力误差,将其加入由 (12)、(13)、(14) 式计算得到的观测值作为起算值。

③ 基于输入量Si、Zi、βi、di的起算值,按照假设的分布,模拟加入影响量,每组样本输入量个数为44个,按照数学模型计算M个mH。

6) 输出量及标准不确定度

标准不确定度:

7) 扩展不确定度

M个mH模拟值服从正态分布,如图8所示。

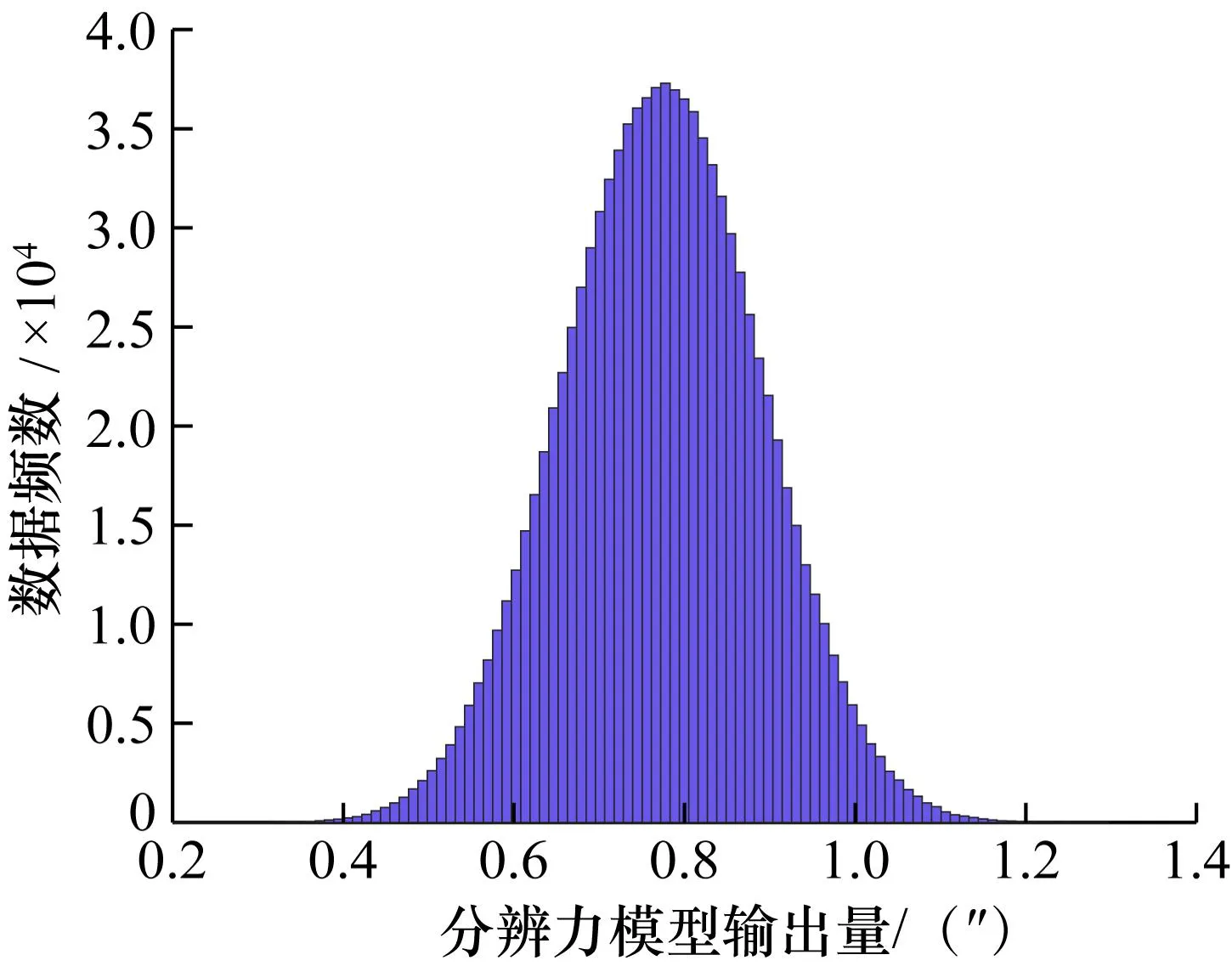
图8 分辨力模拟值分布图Fig.8 Distribution of simulated resolution values

U=k·u=2×0.11″=0.22″

5 应用案例

依据所设计的在线计量方法,在实验室对一台定期进行溯源的TS60测量机器人进行模拟实验,并对武汉市地铁6号线和4号线某2段区间的4台多年未溯源的在线监测机器人进行在线计量(图9)。校准采用分辨力检验台以及长度标尺配合球棱镜作为主标准器,其中分辨力检验台MPE:±0.05 mm,水准标尺不确定度U=0.05 mm,k=2,校准结果见表3。

表3 模拟实验结果及地铁在线校准结果Tab.3 Simulation experiment results and subway on-line calibration results

图9 实验室及地铁现场实验场景图Fig.9 Scene Map of laboratory and Subway Field Experiment

根据校准结果:1) 真实地反映出了5台测量机器人的技术性能和设备状态,定期进行溯源的设备其技术指标较好,长期未溯源的4台设备性能差别较大,其中3台的测角分辨力已经大于本身的测角精度,指标较差; 2) 验证了所使用校准方法的可行性和有效性; 3) 对在线运行的测量机器人的计量性能给出了准确的计量数据,为监测部门判断设备的性能和数据的准确性提供依据。