基于激光扫描仪的点云配准方法

褚海漫, 程银宝, 李亚茹, 罗 哉, 江文松, 王 燕

(1. 中国计量大学，浙江 杭州 310018； 2. 沈阳飞机工业(集团)有限公司，辽宁 沈阳 110850)

1 引 言

近几年,借助激光的手段,机器视觉得到了极大程度的发展,其中产物三维激光扫描仪可实现对空间物体的非接触式测量,1∶1复刻被测物体的三维数据信息,应用广泛。激光扫描仪在扫描过程中受被测物体几何形状、扫描角度因素影响,使得扫描仪在绝大部分情况下无法通过一次扫描获取被测物体表面的全部几何信息,需要对扫描仪多视角扫描结果进行点云配准处理。此外,激光扫描仪用于实际工件扫描得到的点云数据是不完整的,而大多关于点云配准算法的研究是基于完整点云数据,因此有必要对不完整点云数据的配准进行研究。

为了解决这一问题,国内外学者提出了一些基于点云局部特征提取的方法或是对点云数据本身进行处理。Zhao等[1]提出注意力引导网络可利用点之间的相关性提取局部特征,并且可以融合特征实现点云重建填补孔洞对不完整点云进行复原;Chen等[2]提出一种新型神经网络能够学习局部特征并实现对数据集的形状分类及语义分割;Piotr等[3]针对具有复杂几何表面信息且色彩信息丰富但具有几何缺陷的点云提出了快速自适应多模态特征配准;Liu等[4]对于数据量极大特征相似的城市场景点云配准提出了PCRMLP隐式地从实例中估计变换并由多层感知器网络进行实现快速粗配准;Wang等[5]针对低重叠状态配准问题结合密集图卷积和多级交互变压器设计点云配准网络提高了点云特征的提取能力。学者们针对不完整点云的配准问题,首选做法大都是对不完整点云进行补全,并且实现过程较为复杂。

针对不完整点云配准困难的问题,提出了对应点对的配准方法。首先利用激光扫描仪对被测工件进行扫描获得实际点云数据,再将不完整点云进行整体分析,选取不完整点云与理想点云的对应点对进行初始对齐;然后采用最近邻点迭代算法(iterative closest point,ICP)进行精确对齐,并基于Visual Studio 2013软件装配点云库Point Cloud Library1.8.0环境进行实现,使得2点云尽可能重合;最后采用均方根误差作为点云配准精度评价指标对不完整点云的配准精度进行评价,分析配准方法的实用性以及准确性。

2 点云数据获取

2.1 激光扫描仪测量原理

三维激光扫描系统主要由扫描系统、控制系统以及计算机系统3个部分组成,其中扫描系统主要包括激光测距模块以及激光扫描模块,控制系统通过计算机总线控制扫描模块和测距模块以保证扫描工作的正常进行,计算机系统通过系统指令的方式控制仪器工作,并存储测量数据[6,7]。

在实际扫描过程中,首先激光发射器发出激光,激光到达被测物体表面后反射至扫描系统由激光接收器接收,计算激光反射的往返传播时间t、俯仰角θ、水平角φ等数据信息,由往返传播时间t可求出扫描仪到目标物体之间的距离S,再配合扫描仪自身的位置信息[8],即可得到目标位置信息,如图1所示。再根据图1所示的几何关系,可以得到目标点P的三维坐标计算式[9～11]:

(1)

图1 激光扫描仪测量原理Fig.1 Laser scanner measurement principle

式中:S表示扫描仪到目标点之间的距离;θ表示其俯仰角;φ表示其水平角。

2.2 激光扫描仪采样工作

实验所用装置为海克斯康(HEXAGON)AICON测量系统中的便携扫描系统PrimeScan,如图2所示,其精度较高,便携性好,支持多种光源选择。

图2 便携扫描系统Fig.2 Portable scanning system

该三维扫描仪由分布在左右2个高分辨率工业CCD相机以及中央光栅投影单元组成,采用结构光测量,即激光从激光器发出经过柱面透镜后汇聚成宽度很窄的光带,通过光栅投影单元将一组具有相位信息的光栅条纹投影到测量工件表面,并且由左右2个相机进行同步测量。其利用立体相机测量的原理,可以在1 s时间内准确获得200万到1600万个高密度的三维数据点。

三维激光扫描仪校准后即可进行实际工件测量,为执行测量,需要将传感器放在测量对象前面,理想操作距离取决于所选的传感器测量区域,但实际上,最佳工作距离就是2个激光红点重合处,需将其调整到被测物的中心。调整好工件位置和扫描仪角度后,确保2个激光红点重合处在被测物的中心附近,将零件表面待测区域调节至合适颜色(红色,绿色,蓝色)后点击确定进行扫描,颜色显示青色,白色部分无法采点,如下图3所示,因此扫描得到的实际点云为不完整点云。

图3 扫描调整页面Fig.3 Scanning adjustment page

实验被测工件表面较为复杂,且单次扫描无法得到被测物体完整的点云;为使不完整点云配准结果具有可对比性,使用激光扫描仪进行了3次实验。首先选择2个可以采集较多特征的角度进行扫描得到扫描结果1和2,再借助系统软件将扫描结果1和2进行简单拼接生成扫描结果3。系统拼接方式为识别工件特征点拼接,得到工件所需部分的整体点云数据。利用这3组点云数据进行后续配准研究,实验结果如图4所示。

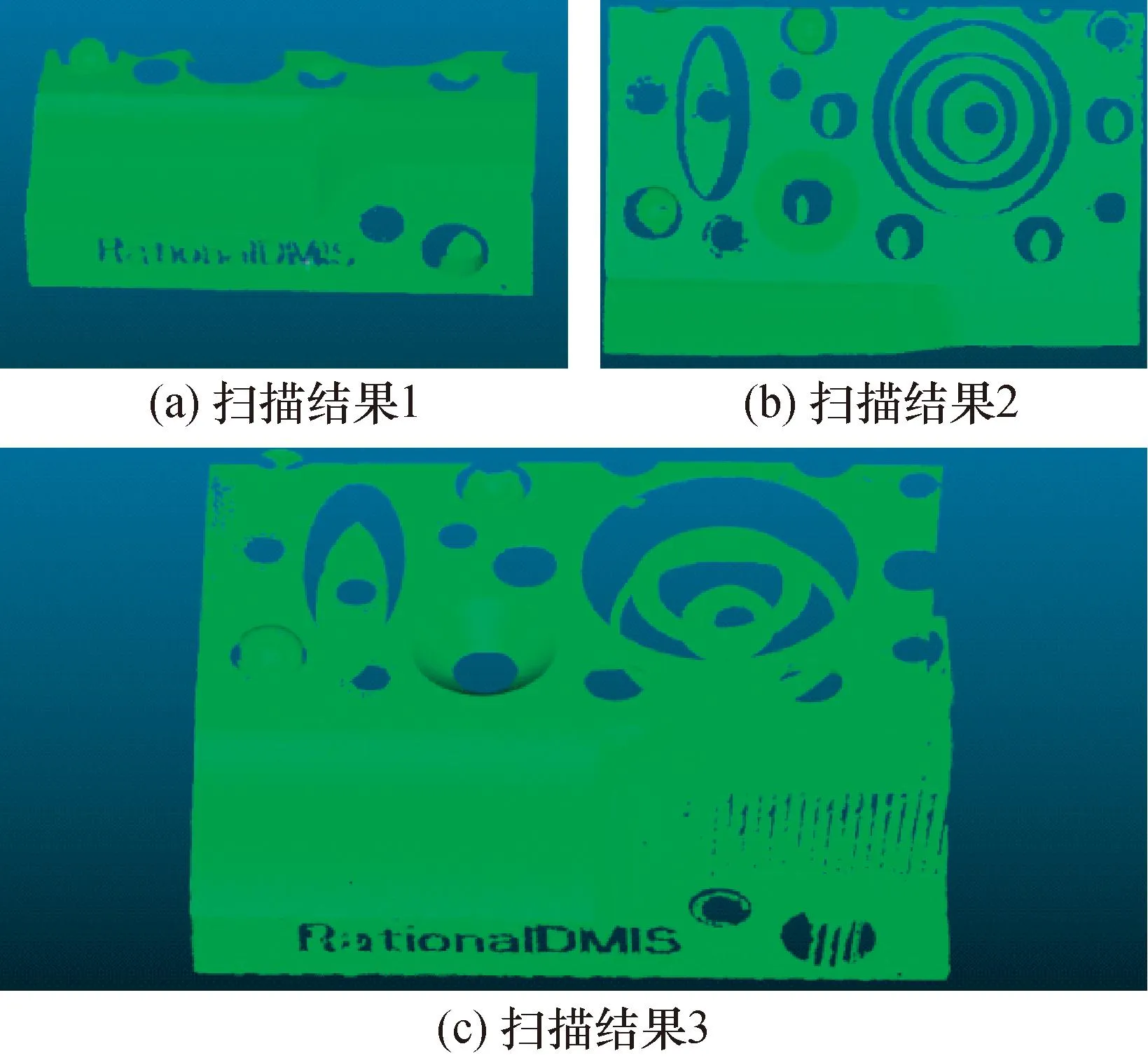
图4 实验扫描结果Fig.4 Experimental scan results

3 点云数据与CAD模型的配准

3.1 点云数据预处理

在进行点云模型的配准之前,需要先对大量的点云数据进行预处理,但在实际测量过程中,由于受到天气、测量误差、视角遮挡等多方面因素影响,将导致收集到的原始点云数据存在许多缺陷,比如噪声点过多、数据不完整、冗杂等。因此,需要对这些点云数据进行处理,当前点云数据处理研究核心主要体现在点云降噪、点云精简以及点云拼接[12]方面。

常用的点云降噪方法包括均匀采样,体素滤波,统计滤波,双边滤波,条件滤波,高斯滤波等[13,14]。初步观察实验对象,发现扫描结果无明显离群点,因此选择采用体素滤波,即对点云数据创建三维体素栅格,用每个体素重心近似代替体素中的其他点。虽然此方法对比均匀采样较慢,但它对于采样点对应曲面的表示更为准确,能够更为准确地保存点云形状特征,帮助后期进行点云配准工作。以扫描结果3为例,进行点云滤波的结果对比,如图5所示。

图5 滤波结果对比图Fig.5 Comparison chart of filtering results

同时,太过庞大的点云数据会影响到数据处理时的精度和速度,也会影响到后期的点云数据配准工作,因此需要对点云数据进行精简。国内外学者经过长期的研究,提出了许多成熟的点云精简算法,这些算法可大致被分为6类[15]:包围盒法、均匀网格法、角度法、RANSAC随机采样一致性算法、三角网格法以及曲面采样算法,本文采用均匀网格法进行点云精简。

3.2 点云配准算法原理

点云配准过程主要分为特征提取、特征匹配和变换参数计算,其中,特征提取和匹配的效果是决定配准精度的核心因素。因此,通常将整个点云配准过程分为点云粗配准(coarse registration)和点云精配准(fine registration)2个阶段。点云粗配准是指在点云相对位姿完全未知的情况下对点云数据进行配准,其主要是为了给点云精配准提供良好的变换初值;而点云精配准的目的是在点云粗配准的基础上使点云之间的空间位置差别最小,其中应用最为广泛的精配准算法是ICP算法以及ICP的各种变种(GICP、NICP)。

(2)

式中:tx表示点P在x轴上的偏移量(ty、tz同理);V表示其在各坐标方向上进行投影变换的比例;U指代整体点云的比例因子,由于通过激光扫描生成的点云数据不会产生奇异变形,故V为零向量,U=1;α表示该点绕x轴顺时针方向旋转角度(β、θ同理)。

点云配准首先是进行点云的特征提取,目前最常用的方法是使用快速点特征直方图,其使用参数的方式查询点云中点与其领域点之间的空间差异,以多维直方图的形式描述点的几何属性。但是由于激光扫描仪扫描工件时需要在工件上贴标记点,扫描后的标记点处呈现未填充的孔洞,同时由于工件表面存在较深的凹槽,很难用激光扫描仪一次性扫描成型,因此会造成部分数据缺失,这些因素导致激光扫描仪实际扫描仅能得到不完整点云。因此想要利用算法在不完整点云上寻找属于工件本身的特征点极其困难,于是采用最方便快捷且适用性强的点对齐方式进行粗配准给精配准提供良好的初始位姿。

ICP算法,或称最近点迭代配准算法,是点云精配准的经典算法。ICP算法本质上是基于最小二乘的最优匹配算法,它重复寻找2点云间的对应点以及最优坐标变换,直至满足某个收敛条件,迭代终止。该算法的目的是找到原始点云与目标点云之间的转换矩阵R和T,使得2点云之间满足某种度量准则下的最优匹配。该算法的基本思想是:先假设一个初始位姿(位置和姿态)估计,从一个视角扫描获得的点集中选出一定数量的点,再从另一视角的扫描获取点集中寻找与这些点对应的距离最近的点集,通过最优坐标变换,使对应点的点集间距离最小化,通过迭代计算,直到残差平方和所构成的目标函数值不变[17]。

设理论目标点云集为Si(i=1,2,…,n),原始测量点云集为Qi(i=1,2,…,n),寻找实际原始测量点云的变换矩阵使得目标函数F(R,T)最小,则其数学模型可表示如下:

(3)

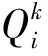
3.3 点云配准算法实现

基于实际激光扫描仪实验生成的被测工件扫描点云数据,使用Visual Studio 2013软件装配点云库Point Cloud Library1.8.0环境,在处理器为AMD Ryzen 5 3550H的电脑上对实验数据进行处理。当前使用软件VS+PCL处理的点云数据多基于PCD文件格式,因此可先通过CloudCompare软件将实验软件导出的STL点云文件格式转换至PCD文件格式,即可按流程图6进行点云配准。

图6 点云配准流程图Fig.6 Point cloud registration flowchart

3组实验数据的配准结果如图7所示,Ⅰ为扫描点云与理想点云的初始位姿可视化,Ⅱ为粗配准后的点云相对位姿可视化,Ⅲ为精配准后转换点云与理想点云可视化。

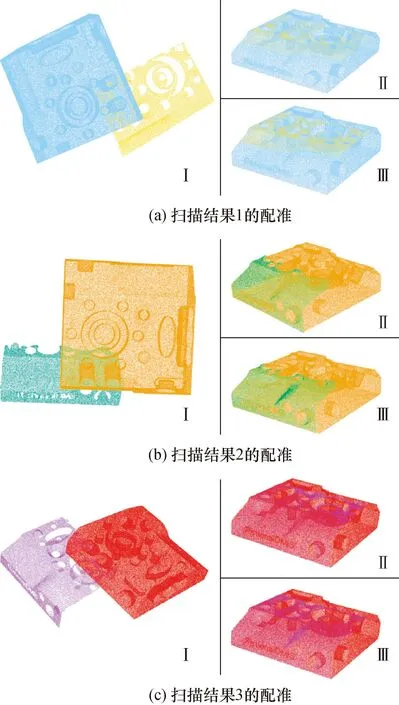
图7 扫描结果的配准Fig.7 Scan result registration

4 点云配准精度评价

4.1 精度评价指标

点云配准的最终结果需要有一个评价指标进行评价衡量,均方根误差SRMSE的定义是衡量预测值与真实值之间的偏差,可将其转用于点云配准精度的评定,作为点云配准精度评价指标,其定义式如下:

(4)

4.2 评价结果

对3组点云数据均进行了点云配准,以点云配准后的转换点云与目标点云之间的均方根误差SRMSE为评价指标评估点云配准精度,具体结果如表1所示。

表1 点云配准精度

点云配准精度越高,其均方根误差越小,设置精配准最大迭代次数为40次时,均方根误差可控制在0.62 mm。

ICP算法本质上是寻找最近邻点对不断地进行目标逼近,因此应用此算法可以实现扫描点云与理想CAD模型配准。然而,ICP算法的配准精度会非常依赖变换初值的准确度。为了评价迭代过程中ICP算法的具体配准情况,列出扫描数据的迭代收敛图,分别计算ICP算法在迭代10,20,…,40,50次时,扫描点云与理想点云的配准精度。

通过如图8所示的数据分析,对于给定的不同精度粗配准数据结果,ICP算法在迭代10次的时候均可达到0.70 mm左右的配准精度;再进行迭代后配准精度变化很小,并且在迭代40次后,配准精度变化微小,已趋于稳定。

图8 扫描数据的迭代收敛图Fig.8 Convergence diagram of iterative alignment accuracy of scanned data

实验表明,ICP算法可以极好地适用于本文粗配准后得到的配准结果,并且能在仅迭代10次时就能达到较好的配准精度。然而,精配准的主要目的是增加配准精度,减小均方根误差值,使实际扫描的点云数据与CAD模型之间尽可能重合。因此,继续进行ICP算法迭代,确定在迭代40次时,算法对本文实验数据所能达到的配准精度已趋于稳定。

配准精度的评价指标均方根误差实际上是寻找目标点云与转换点云的近邻点对,计算点对之间的平均距离。因此,对于不同的实验对象,均方根误差的数据量级也不尽相同。CloudCompare软件可以进行点云与点云之间的最近邻距离计算,并用颜色进行区分,具体表现如图9所示(以第3组点云数据为例)。

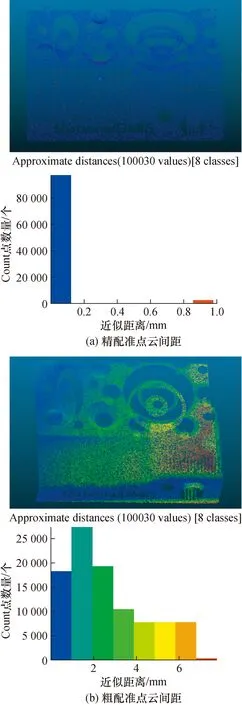
图9 配准点云间距Fig.9 Distance between point clouds

由图9(a)可以看出,转换点云中的绝大部分点与目标点云中识别的对应点距离小于0.15 mm(图9(a)中蓝色数据),表明其能够精确配准到目标点云上。但是剩下的小部分点与目标点云距离大于0.85 mm(图9(a)中红色数据),表明其未实现最优配准。此外,实现最优配准的点数量与未实现数量之比约为39:1,即实现最优配准的点数量远大于非最优配准点。由于被测工件在制造时表面便存在一定的加工误差,而点云配准的目标模型是该工件的理想CAD模型,这部分距离差较大,未完全与目标点云重合的点极大可能是由于该工件加工误差产生的,从而也导致了点云配准的均方根误差不能趋近于0。

点云配准在最优理想状态下均方根误差可达到0,但是由于被测工件本身存在加工误差,所以将被测工件的实际点云数据与其理想CAD模型进行点云配准,最终得到点云配准的均方根误差不可能为0。通过采用纵向对比的方式,借助CloudCompare软件显示粗配准状态下得到的点云,计算其与目标点云之间的最近邻距离以及均方根误差,结果如图9(b)所示(同样以第3组点云数据为例)。粗配准均方根误差SRMSE为1.23 mm。将粗配准点云间距图9(b)与精配准点云间距图9(a)相比,可以直观地发现,将经过点对齐粗配准后的点云数据经由ICP算法进行精配准,得到的点云配准结果可满足工件检测要求。

5 结 论

提出了一种对应点对的方法用于扫描点云数据与CAD模型之间的粗配准。此方法可较好地应用于不完整点云配准,再使用ICP精配准算法进行精细配准。点云配准完成后对配准精度进行了评价,使用均方根误差作为评价指标,粗配准的均方根误差为1.23 mm,精配准的均方根误差为0.62 mm,配准精度提高了49.59%,表明了所提出方法能为ICP算法提供一个很好的初始值,使得配准效果有所提升。

将ICP算法在精配准过程中迭代次数对应的配准精度进行比较,结果表明3组扫描数据均在迭代10次时已有较好的配准效果,在迭代40次时,配准精度趋于稳定,均方根误差可控制在0.62 mm。由于被测工件表面存在一定的加工误差,所提出的配准方法得到的结果可满足工件要求。但是,为测试所提出的配准方法的可行性,选择事先设定实验对象配准的迭代次数作为迭代终止条件。在实际工业生产过程中,应是以要求的工件配准精度标准作为迭代终止条件,实现自动化配准,以更快更准确地完成目标。