高中数学“变式教学”策略例谈
2024-04-18王传英山东省临沂市兰陵县第二中学
王传英 (山东省临沂市兰陵县第二中学)
变式教学指的是从不同层次对具体问题进行变式设计,采用题组形式引导学生分析问题的本质,便于掌握解决问题的基本方法。变式训练激活了学生的数学思维,不仅帮助他们构建完整的知识体系,还在无形中加深对数学思想和方法的理解,充分锻炼其思维的广阔性和创新性。
一、高中数学变式教学的相关概述
(一)变式教学的概念
变式教学是指对数学问题进行多层次、多角度、多情形的变式设计,帮助学生理清问题本质,总结出不同知识点间关联性的教学方法。具体来说,变式教学是由教师根据本课所学内容布置一道针对性例题,由学生自主探究解题方法,通过独立思考或合作探究的方式得出最终结论。然后再由教师创编相同类型的题目供学生练习,在不断尝试中掌握此种解题技巧。或是学生自主设计相关例题,在发现、提出、分析、解决问题的过程中使其数学思维更加灵活。
(二)变式教学的意义
1.激发学生的学习兴趣。在高中数学课堂中运用变式教学,可以为学生提供求异、思辨的空间,起到激发学生学习兴趣的作用。与传统教学模式相比,变式教学更贴合高中生的认知规律和发展需求,多变的例题使数学学习充满挑战,在好奇心的驱使下主动探寻知识点之间的内在联系,学会透过问题看本质,从而快速理清解题思路,保证问题的顺利解决。
2.提高学生的归纳能力。变式训练改变的是问题结构或呈现形式,启发学生积极思考,踊跃参与到各项活动中,将本节课收获的理论知识灵活运用于实际,在变化的题目中总结出不变的本质,更好地掌握数学规律,彰显变式教学对提高学生归纳能力的重要影响。也就是说,学生在思考问题时不仅要认真观察题目,梳理题干中的关键信息,还要总结不同例题之间的相同点,使其归纳能力和分析能力得到增强,变式教学的实施为培育数学核心素养创造了有利条件。
二、基于思维能力培养的高中数学变式教学策略
(一)在概念生成处变式,培养思维的灵活性
概念是高中数学教学的基础性内容,在教学过程中,很多例题都是以概念为核心进行设计的,为了帮助学生深化知识理解,教师可以在概念生成处进行变式训练,从最简单的问题入手,而后逐渐增加难度。学生在循序渐进地练习中产生自己的感悟与体会,形成重点概念全新认知,学会从不同维度分析问题,充分锻炼其数学思维的灵活性。
以人教版《普通高中教科书·数学》选择性必修第三册(A版)中《排列与组合》为例,本课包含的概念有排列定义、组合定义等。
案例1:判断下列问题是否是排列问题?(1)从2,3,5,7,11中任取两数相乘可得多少个不同的积?(2)从上面个数中任取两数相除,可得多少个不同的商?
解析:(1)乘法符合交换律与顺序无关,不是排列问题。(2)上、下互换结果不一样,与顺序有关,是排列问题。
变式:餐桌上有5盘不同的菜,甲、乙、丙3位同学每人从中各取1盘菜,共有多少种不同的取法?
解析:可以先让甲从5盘菜中选1种,有5种选法;再让乙从5盘菜中选1种,也有5种选法;最后让丙从5盘菜中选1种,同样有5种选法,根据分布乘法计数原理,不同的选法种数为:5×5×5=125 。
以上例题检验学生对排列概念的掌握程度,同时加强他们对知识点的理解与运用。这样的变式对学生深刻领悟排列概念内涵以及应用方法具有积极影响,其思维能力也得到一定提升。
(二)在易犯错误处变式,培养思维的准确性
教师要留心观察学生的课堂表现,重点关注他们在解题中的“易错点”,以此为依据展开变式教学,让学生在反复练习中发现问题所在,有利于强化新知的理解与运用。
以人教版《普通高中教科书·数学》选择性必修第三册(A版)中《条件概率与全概率公式》为例,部分学生经常在摸球问题中出错,教师出示具体例题:
案例2:在一个袋子中装有10个球,设有1个红球,2个黄球,3个黑球,4个白球,从中依次摸2个球,求在第一个球是红球的条件下,第二个球是黄球或黑球的概率。
解析:设“摸出第一个球为红球”为事件A,“摸出第二个球为黄球”为事件B,“摸出第2个球为黑球”为事件C。则
变式:设袋中有5个红球,3个黑球,2个白球,有放回时摸球三次,每摸一次球,求第三次才摸到白球的概率。
解析:设“第一次未摸到白球”为事件A,“第二次未摸到白球”为事件B,“第三次摸到白球”为事件C。则
在同类型习题的计算中,学生掌握了条件概率的相关内容,引导他们运用条件概率及概率乘法公式解决实际问题,找出“易错点”后经过变式训练提高解题正确率和思维准确性。
(三)在知识交汇处变式,培养思维的广阔性
高考数学命题是从学科整体的角度出发,以知识点之间的关联性为依据进行设计的,目的在于检验学生是否具备网格化的知识体系,重点考察她们对所学内容理解的深度和广度。教师应将重点内容与之前学过的数学知识加以整合,深入研究知识间的联结点,进行有意义的变式设计,为学生提供多元化的复习渠道,起到培养思维广阔性的作用。
以人教版《普通高中教科书·数学》选择性必修第三册(A版)中《分类加法技数原理与分步乘法计数原理》为例。
案例3:假如某人有壹元、贰元、伍元、贰拾元、伍拾元、壹佰元的纸币各两张,要支付贰佰壹拾玖元的款项,有多少种不同的支付方式?
解析:9元的支付有2种情况,5+2+2或5+2+1+1。(1)当9元采用5+2+2方式支付时,200元的支付方式有2×100或1×100+2×50或1×100+1×50+2×20+10共三种方式,10元的支付只能用1张10元,此时共有1×3×1=3种支付方式。(2)当9元采用5+2+2+1方式支付时,200元的支付方式为2×100或1×100+2×50或1×100+1×50+2×20+10共3种方式。10元的支付方式只能用1张10元,此时有1×3×1=3种支付方式,所以总的支付方式共有3+3=6种。
变式:乘积(a1+a2+a3)(b1+b2+b3+b4)(c1+c2+c3+c4+c5)展开后共有多少项?
解析:根据多项式的乘法法则,题干中的每一项都必须是在(a1+a2+a3),(b1+b2+b3+b4),(c1+c2+c3+c4+c5)三个式子中任取一项后相乘,在(a1+a2+a3)中有3种取法,在(b1+b2+b3+b4)中有4种取法,在(c1+c2+c3+c4+c5)中有5种取法,由乘法原理可得,共有3×4×5=60种情况。
在知识交汇处变式,学生不仅掌握了本课内容的核心,还在变式中结合以往学过的理论知识进行分析,起到良好的复习效果。将分布乘法计算原理与多项式乘法法则结合在一起,使学生学会从不同视角探索解题方法,促进广阔性思维的进一步发展。
(四)在拓展延伸处变式,培养思维的深刻性
为了帮助学生全面地理解所学内容,教师可以在拓展延伸处进行变式训练,适当增加题目难度,引导学生从简至繁,探究新知。
以人教版《普通高中教科书·数学》选择性必修第三册(A版)中《二项式定理》为例,要求学生知道二项式定理的概念,展开式和系数。
案例4:(1+x)+(1+x)2+...+(1+x)7展开式中,x3项的系数为_____。解析:x3项的系数为
变式1:设(x+a1)(x+a2)(x+a3)(x+a4)=(A0x4+A1x3+A2x2+A3x+A4),则A2=_____;A3_____.解析:A2是x2的系数,即从{ a1,a2,a3,a4}中各取两元的所有组合的和,即A2=a1(a2+a3+a4)+a2(a3+a4)+a3a4,同理A3=a1a2a3+a1a2a4+a1a3a4+a2a3a4。
变式2:(x2-x+1)10展开式中x3的系数为_____。
解析:本题不利于展开所有项,所以考虑将其转化为10个因式如何分配所出项的问题,若要凑成x3有以下几种可能:(1)1个x2,1个(-x),8个1, 所得项为:(2)3个(-x),7个1,所得项为,所以x3项的系数为-210.
教师设计了不同难度的变式内容,始终将学生的实际需求放于首位,引领他们不断深入研究二项式定理的相关知识,在不同难度的变式训练中完成知识的内化,使其数学思维变得更加愈发深刻,促进学生思维能力的全面发展。
(五)在思想方法处变式,培养思维的创新性
教师在变式教学中要将数学思想方法渗透于典型例题,让学生在潜移默化中感受到它的重要性,主动关注思想方法的形成与发展,在不同类型习题的辅助下产生新颖的解题思路,有利于创新精神的培养。
以人教版《普通高中教科书·数学》选择性必修第三册(A版)中《成对数据的相关关系》为例,主要内容是通过收集现实问题中的两个有关联变量的数据认识变量间的相关关系。
案例5:下列两个变量之间的关系哪个不是函数关系。( )A.角度和它的正切值;B.人的右手一柞长和身高;C.正方体的棱长你和表面积;D.真空中自由落体运动物体的下落距离和下落时间。
解析:A选项,角度和正切值有确定的关系y=tan x;B选项,人的右手一柞长和身高不具有统一关系;C选项,正方体的棱长和表面积有关系x=6a2。D选项,真空中自由落体运动的下落距离和下落关系所以选择B。
变式:某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下表。根据表中数据,利润率与人均销售额成_____关系。
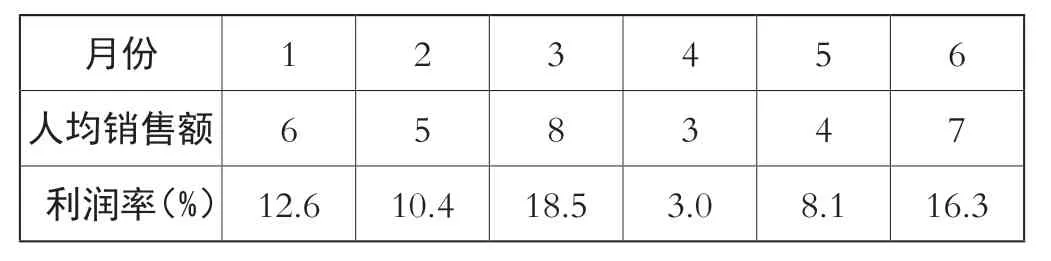
月份1 2 3 4 5 6人均销售额6 5 8 3 4 7利润率(%)12.6 10.4 18.5 3.0 8.1 16.3
解析:教师引领学生根据表格数据自行绘制利润率与人均销售额的散点图,在直观图像的帮助下能够得出“利润率与人均销售额成正相关关系”的结论。
本节课的变式训练使学生体会到数形结合思想的应用价值,可以将原本抽象的已知条件以形象的方式呈现,通过画图的方法得出关键信息,便于问题的顺利解决。此种训练也使学生的创新性思维得到激发,摆脱了传统解题模式的束缚,逐渐形成全新的解题思路,为日后长远的数学学习之路打好基础。
