单/双站辅助的干涉仪标校与选站方法
2024-04-18宋逸豪黄普明刘波冯雪峰李帅张千
宋逸豪 黄普明 刘波 冯雪峰 李帅 张千

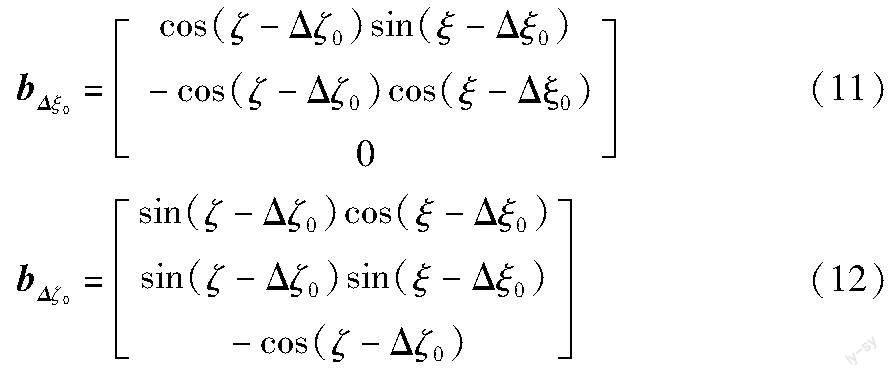
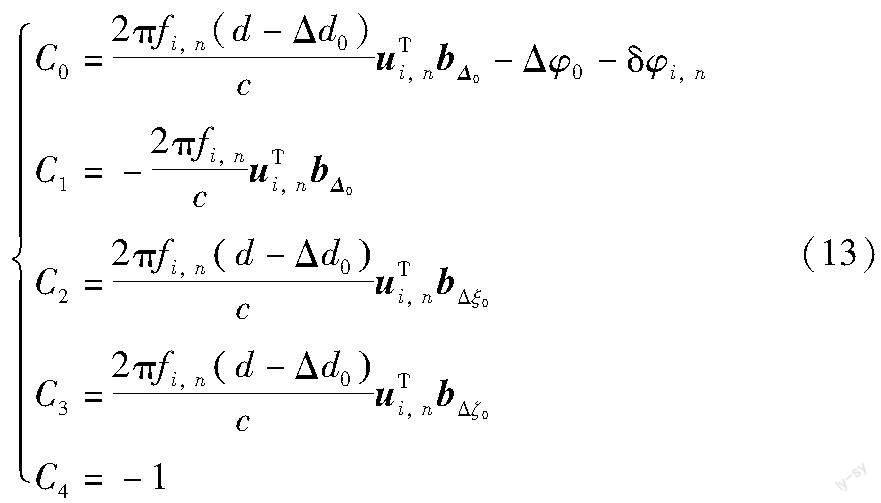
摘 要: 传统的固定基线干涉仪多误差联合标校方法需要三个以上的标校站才能实现干涉仪的在轨实时标校, 但是在标校站数量不足时传统方法性能将降低甚至失效。 针对标校站数量不足的情况, 本文提出一种固定基线干涉仪单/双站标校算法。 在干涉仪与标校站之间存在相对运动的条件下, 首先通过多次测量获得一组标校信号相位差, 其次利用所得相位差列出关于干涉仪各项系统误差的方程组, 最后使用Penrose逆矩阵辅助的迭代最小二乘法求解出各项系统误差值。 仿真结果验证了所提算法的可行性。 在此基础上, 针对标校站选址对标校后干涉仪定位性能影响的问题, 分解标校站选址的各项指标, 通过数值仿真的方式, 定性分析了标校站选址的各个参数对干涉仪定位精度的影响。 分析结果表明, 单站情况下位于星下点附近的标校站或双站情况下相距较远的两个标校站均能让标校后的干涉仪获得更优的定位性能。
关键词: 干涉仪; 标校; 系统误差; 单站; 双站
中图分类号: TJ760; TN971
文献标识码: A
文章编号: 1673-5048(2024)01-0122-06
DOI: 10.12132/ISSN.1673-5048.2023.0089
0 引 言
干涉仪测向方法是无源测向定位的重要手段之一, 它通过对到达波信号到达不同接收器之间的相位差进行处理来获取到达波的到达方向, 进而计算出辐射源的位置[1-3]。 干涉仪具有较高的测向精度且可以实现单脉冲测向, 因此被广泛地应用于声呐、 雷达等电子侦察相关领域。 不过, 受限于器件、 设备的工艺水平和机械结构的控制水平等, 在复杂环境的影响下, 工作过程中的干涉仪会存在多项系统偏差, 对测向精度产生较大的影响。 例如, 各个接收通道之间的幅/相不一致性会导致测量相位差出现偏差; 连接杆的伸缩、 旋转等活动会造成两阵元间基线的长度和角度出现偏差; 干涉仪平台对本身姿态的控制和测量也会存在一定的偏差。 这些偏差最终都会影响到两通道间接收信号相位差的测量结果, 对波达方向的估计产生影响, 造成测向精度的降低。
为了提高测向精度, 干涉仪需要对自身的各种误差进行标定和校正(简称标校)。 许多学者对此进行了深入研究。 文献[4]研究了干涉仪的静态标校方法; 文献[5]通过求解线性方程组在两个标校站的辅助下校正了干涉仪的空间指向; 文献[6]使用总体最小二乘法分别在静态标校和动态标校的条件下分离了接收信号中的目标信号与噪声, 对接收通道进行了校正; 文献[7]利用干涉仪自身的运动特性通过单个长基线测量模糊相位差, 联合估计出辐射源位置和相位差偏差; 文献[8]提出了一种标校站辅助的对不同系统误差的非线性最小二乘联合估计方法, 能同时有效估计出多种系统误差; 文献[9]利用迭代最小二乘法对旋转干涉仪的多种系统偏差进行校正, 提升了系统性能。
以上研究成果能够满足常规环境下的干涉仪标校需求, 但是固定基线干涉仪的多项系统误差需要用到多个标校站辅助标校工作。 考虑到星载干涉仪可侦察范围大, 在有侦察需求时波束范围内可能没有足够数量的标校站, 于是有必要讨论依托仅有的标校站或者其他位置、 信号已知的广播站(如电视台)等来辅助完成标校工作。 本文开展了在干涉仪波束范围内仅有一个或两个标校站时的干涉仪标校算法研究, 提出了一种适用固定基线干涉仪单/双站的多误差联合标校算法。 考虑到星载干涉仪可以通过姿态控制调整波束方向, 本文讨论了在卫星可视范围内存在多组可选择的标校站时的选站问题, 定性分析了标校站布局对干涉仪定位精度的影响。
1 干涉仪误差模型分析
根据干涉仪测向原理[10], 两阵元接收到信号间的无模糊相位差為
式中: c为光速; f为来波频率; d为基线长度; u为本体坐标系下的目标视线单位矢量; b为干涉仪基线的单位矢量。 假设在测量时刻基线在本体坐标系下的旋转角或方位角为ζ, 俯仰角为ξ, 那么干涉仪基线的单位矢量b可以表示为
假设在测量时刻主阵元的位置坐标为xO, 目标的位置坐标为xT, 那么本体坐标系下的目标视线单位矢量u可以表示为
由式(1)~(3)可知, 能够影响干涉仪定位的误差有: 测量相位差误差、 信号载频测量误差、 基线长度误差、 基线的方位角误差、 基线的俯仰角误差以及平台位置误差。 误差由系统误差和随机误差两部分组成。 系统误差由器件本身造成, 可以认为在一次测量的多次采样过程中是保持不变的; 随机误差由测量过程中的各种不稳定随机因素造成, 每次采样都会产生不同的随机误差。 标校工作的目的是标定和校正干涉仪的系统误差。
在典型应用条件下, 信号载频测量误差和平台位置误差对定位结果的影响较小, 通常在标校过程中可以忽略; 基线长度误差和基线的方位角误差对定位结果影响较大, 在标校过程中应考虑予以校正; 测量相位差误差和基线的俯仰角误差对定位结果影响最大, 在标校过程中必须得到校正[8]。 因此, 标校工作一般会考虑基线的长度误差、 方位角误差和俯仰角误差以及测量相位差误差4项系统误差。
其中, 基线的长度误差、 方位角误差和俯仰角误差由干涉仪安装过程中的测量和安装精度、 干涉仪本身和所在平台自身姿态的控制精度共同决定; 测量相位差误差是整个接收环节中各器件工作产生的幅相误差累加而成, 包括接收天线、 接收机、 鉴相器以及连接各器件的馈线产生的各类误差。 由于基线的长度、 方位角和俯仰角无需实时测量, 因此可以认为在一次测量过程中这三者的随机误差为0。 用下脚标t的变量符号来表示该变量的真值, 否则表示该变量的测量值, 则有
式中: Δd, Δξ, Δζ, Δφ分别为基线长度、 方位角、 俯仰角以及测量相位差的系统误差; δφ为测量相位差的随机误差, δφ服从均值为0、 方差为σ2的高斯分布。 在考虑误差后, 两阵元接收到信号间的无模糊相位差为
由式(5)可知, 如果能对各项系统误差进行精确估计, 就能有效提升干涉仪定位的精度。
2 系统误差联合估计方法
假设标校站的位置和发射信号频率已知, 向运动中的干涉仪不间断地发送标校信号, 干涉仪可以通过导航系统得知自身的位置。 在接收到标校信号后, 通过比较测量到的标校信号相位差与计算得到的理论标校信号相位差, 干涉仪可以对各个系统误差量进行估计。 通过将系统误差的估计值与原本的测量值相加, 即可得到标校后真值的估计值。 为了减小运算量, 并提高估计精度, 本文使用高斯-牛顿法(G-N法)对系统误差值进行估计。
设定系统误差向量为
Δ=ΔdΔξΔζΔφT (6)
bΔ为考虑误差后的基线单位矢量记, 即
那么, 在某次测量中的测得的第i个标校站发出信号的第n次采样得到的无模糊相位差为
将式(8)在Δ0=Δd0Δξ0Δζ0Δφ0T处泰勒展开, 忽略随机误差项, 可以得到
式中: bΔ0为bΔ在Δ0处的值, 即
bΔξ0和bΔζ0分别为bΔ在Δ0处对Δξ和Δζ求导的结果, 即
记
将式(13)代入式(9), 保留一阶项, 则有
φi, n=gi, n(Δ)|Δ0=C0+(Δd-Δd0)C1+
(Δξ-Δξ0)C2+(Δζ-Δζ0)C3+
(Δφ-Δφ0)C4(14)
经整理可得
C1Δd+C2Δξ+C3Δζ+C4Δφ=φΔ-C0+C1Δd0+C2Δξ0+C3Δζ0+C4Δφ0 (15)
令
在標校测量过程中, 对每个标校信号的每次采样都能得到一组Ai, n和Bi, n。 将测量得到的所有采样结果结合, 可得到如下两个矩阵:
通过式(17)两个矩阵可联立得到关于干涉仪系统误差的一阶线性拟合方程组, 即
ΑΔ=Β(18)
由于随机误差的存在, 使得直接求解式(18)方程会得到偏差较大的解。 用最小二乘法求解该方程可得到干涉仪系统误差的估计:
当标校站数量较多时, 由于每个标校站的目标视线向量间存在较大的夹角, 在多次采样后方程系数矩阵A可以达到满秩状态, 此时ATA为一个非奇异方阵, 它的逆矩阵存在且唯一。 随着标校站数目的减少, 直至只有一个或两个标校站时, 每次采样的目标视线向量间只会由于干涉仪平台自身运动而产生微小的角度变化。 由于随机误差的存在, 在采样间隔较小时, 多次采样后的方程系数矩阵A存在非常相近的特征向量, 此时ATA会近似成一个奇异方阵, 致使式(19)无法求解。
为了解决上述问题, 本文用ATA的Penrose逆代替其逆矩阵代入式(19)中进行运算。 Penrose逆是矩阵的广义逆的一种, 它同时满足全部Moore-Penrose条件[11]。 对于任意方阵, 它的Penrose逆存在且唯一。 当该方阵非奇异时, 其逆矩阵与Penrose逆相等。 本文利用奇异值分解的方法来求取矩阵的Penrose逆。
令P=ATA, 设定奇异值容差, 对P进行奇异值分解:
式中: S为对角阵, 对角线上的值为从大到小排布的矩阵特征值, 即S=diag{σ1, σ2, …, σr}。 将大于容差的特征值组成的对角阵记为S1, 其余的记为S2。 U1、 U2和V1, V2为相应的酉矩阵。 将S2中的奇异值近似为0, 则有
P=U1S1VH1(21)
因此, 可以求得P的Penrose逆为
P+=V1S-11UH1(22)
将式(22)代入式(19)可得, 对于单个或两个标校站也可适用的干涉仪系统误差的估计结果为
一次最小二乘法求解得到的结果往往与真实值仍具有一定的偏差, 使用迭代运算可以减小这个偏差。 将本轮运算得到的系统误差结果作为下一轮运算的系统误差初值, 每轮运算结束后比较本轮与上一轮的运算结果, 若差值小于设定门限值或迭代次数达到设定门限, 则将本轮运算结果作为计算所得的系统误差结果输出。
本文干涉仪系统误差估计方法的主要流程如下:
步骤1: 将系统误差Δ的初始值设为0;
步骤2: 根据式(16)~(17)得到方程的系数矩阵A和B, 并列出方程(18);
3 仿真分析
为了评估本文所提的干涉仪标校算法性能, 对算法进行数值仿真。
设定搭载干涉仪的卫星平台飞行在距地面800 km高度的圆轨道中, 此时卫星的飞行速度为7.45 km/s。 将地面近似为一个平面处理。 设定零时刻卫星在地面上的投影为坐标原点, 卫星飞行方向为x轴正方向, z轴垂直于地面所在平面指向上。 星上搭载一个十字基线干涉仪, 四条基线的长度依次为1.1 m, 1.2 m, 2.1 m, 2.0 m, 方位角依次为0°, 90°, 180°, 270°, 俯仰角均为0°。 设定系统误差如下: 最大测量相位差误差为15°、 最大基线长度误差为4 mm、 最大基线方位角误差为0.15°、 最大基线俯仰角误差为0.15°, 每条基线的每项系统误差独立, 服从均值为0的均匀分布。 设定测量相位差的最大随机误差为5°, 每条基线每次采样结果独立, 且服从均值为0的正态分布。
为了能够更加准确地分析算法, 本文采用Monte- Carlo试验对算法进行仿真, 并通过仿真结果的均方根误差(RMSE)来进行评估。
假设地面上存在一个非合作目标辐射源和若干个已知的标校辐射源。 非合作目标辐射源在每次试验时随机位于距离原点800 km内的某处, 信号频率为4~6 GHz的随机值; 标校辐射源在每次试验时随机散布在距离原点400 km的范围内, 标校信号频率为(6+0.15i)GHz, 其中i为标校站序号。 设定干涉仪每0.2 s对到达信号进行一次采样并获得测量相位差, 每次测量进行300次采样, 进行500次Monte-Carlo试验, 当标校站数量由0个(不进行标校)逐步增加到4个时, 使用各种方法标校后对非合作目标定位距离偏差的RMSE如图1所示。 可以看出, 相较于其他文献中提到的只对某项进行校正的方法, 本文提出的对多误差联合校正的方法能够有效提高定位精度, 并解决了传统的多误差联合校正方法中在单/双站情况下难以解算的问题。
由于测量相位差随机误差的存在, 在相同采样次数的条件下, 更多的标校站能提供更多的采样数据, 因此相较于标校站较少的情况能得到更好的标校结果。 图2展示了在保持采样总时间不变的前提下, 通过改变采样频率以调整总采样点数后, 使用本文所提的标校算法标校后对非合作目标定位距离偏差的RMSE。 可以看出, 对于单站和双站, 通过减小采样间隔来增加采样点数, 能够有效提高定位精度。
4 选站方案分析
4.1 单标校站选站方案分析
在波束范围内只有一个可用的标校站时, 标校站的位置可以用站与星下点之间的距离以及站与星下点连线同卫星运动方向之间的夹角两个维度来表征, 因此用极坐标来描述标校站的位置。 干涉仪与卫星平台的设定与仿真分析时的设定相同, 同时保持相同的系统误差与随机误差的设定, 分别对标校站在不同距离和夹角的情况下干涉仪标校后的定位精度进行仿真, 图3为距离对定位精度的影响, 图4图为夹角对定位精度的影响。
由于随机误差的存在, 仿真结果存在一定的抖动, 不过仍然能够看出相应变量对定位精度影响的趋势。 为了使趋势更加清晰明确, 对单标校站与星下点距离对定位精度影响的仿真结果进行了线性拟合, 对单标校站与星下点连线夹角对定位精度影响的仿真结果进行了正弦曲线拟合, 可以认为, 拟合过后的曲线能够代表相应变量变化对结果带来的影响趋势。
由图可以看出, 在单标校站的条件下, 标校站位置距离星下点的距离越远, 干涉仪的定位精度越低; 标校站和星下点之间的连线与干涉仪平台飞行方向所在直线的夹角越小, 干涉仪的定位精度越高。 从定位精度的变化率分析, 标校站位置与星下点之间的距离对定位精度的影响更大。 因此, 当只有单标校站可以选择时, 应优先选择距离星下点距离近的标校站。
4.2 双标校站选站方案分析
为了方便讨论两个标校站位置对干涉仪定位精度的影响, 将每个标校站的位置由下列4项数据来表示: 两标校站连线中心与原点之间的距离L、 两标校站连线中心到原点的连线与卫星飞行方向之間的夹角α、 两标校站之间的距离D、 两标校站连线与卫星飞行方向所在直线之间的夹角β, 具体如图5所示。
通过仿真分析可知, 当存在多组双标校站可供选择时, 两个标校站之间距离对标校后定位精度的影响最大, 为了能够在标校后达到更好的定位精度, 应当优先选择两个标校站之间距离较远的那一组; 标校站连线中心到原点之间距离也对标校后的定位精度有一定的影响, 距离较近的一组能够得到更优的定位精度; 两标校站连线中心到原点的连线与卫星飞行方向之间的夹角与两标校站连线与卫星飞行方向所在直线之间的夹角对标校后的定位精度基本没有影响。
5 结 束 语
本文针对干涉仪的单站和双站标校开展了研究, 提出了一种干涉仪单站和双站标校的算法, 算法基于干涉仪多次测量的数据, 利用Penrose逆矩阵辅助的迭代最小二乘法求解出各项系统误差值, 并通过数值仿真的方法对单站和双站情况下干涉仪标校站的选站方案做出了定性的分析。 结果表明: 单站情况下位于星下点附近的标校站能让标校后的干涉仪获得更优的定位性能; 双站情况下相距较远的两个标校站能让标校后的干涉仪获得更优的定位性能。
参考文献:
[1] 潘玉剑, 宋慧娜. 基于混合基线的任意平面阵列干涉仪测向方法[J]. 电子与信息学报, 2021, 43(12): 3703-3709.
Pan Yujian, Song Huina. Direction Finding Method with Arbitrary Planar Array Based on Mixed Baselines[J]. Journal of Electronics & Information Technology, 2021, 43(12): 3703-3709. (in Chinese)
[2] 张敏, 张文俊, 李曦, 等. 基于长基线干涉仪相位差的多站无源定位方法[J/OL]. 电子与信息学报, 2023. DOI: 10.11999/JEIT221362.
Zhang Min, Zhang Wenjun, Li Xi, et al. Passive Localization by Multiple Observers Based on the Phase Difference of the Arrival of a Long Baseline Interferometer[J/OL]. Journal of Electronics & Information Technology, 2023. DOI: 10.11999/JEIT221362. (in Chinese)
[3] Li S, Liu Y S, You L, et al. Covariance Matrix Reconstruction for DOA Estimation in Hybrid Massive MIMO Systems[J]. IEEE Wireless Communications Letters, 2020, 9(8): 1196-1200.
[4] 章宏权, 黄劼. 机载干涉仪阵列地面静态标校系统研究[J]. 新型工业化, 2015, 5(6): 59-64.
Zhang Hongquan, Huang Jie. Research on Static Ground Calibration System of Airborne Interferometer Array[J]. The Journal of New Industrialization, 2015, 5(6): 59-64. (in Chinese)
[5] 钟丹星, 杨争斌, 周一宇, 等. LBI测向定位系统的多标校源校正算法[J]. 系统工程与电子技术, 2008, 30(5): 960-963.
Zhong Danxing, Yang Zhengbin, Zhou Yiyu, et al. Multi-Source Calibration for LBI Direction Finding and Location System[J]. Systems Engineering and Electronics, 2008, 30(5): 960-963. (in Chinese)
[6] 丁艺凯. 干涉仪通道误差校正及信号采集电路设计[D]. 西安: 西安电子科技大学, 2010.
Ding Yikai. Interferometer Channel Error Correction and Signal Acquisition Circuit Designing[D]. Xian: Xidian University, 2010. (in Chinese)
[7] 张敏, 郭福成, 周一宇, 等. 运动单站长基线干涉仪自校正定位方法[J]. 宇航学报, 2013, 34(9): 1266-1273.
Zhang Min, Guo Fucheng, Zhou Yiyu, et al. A Single Moving Observer Auto-Calibrated Localization Method Using LBI[J]. Journal of Astronautics, 2013, 34(9): 1266-1273. (in Chinese)
[8] 何朝鑫, 张敏, 郭福成. 基于多标校站的干涉仪系统误差校正方法[J]. 航天电子对抗, 2015, 31(3): 1-5.
He Chaoxin, Zhang Min, Guo Fucheng. Calibration Method of Interferometer Based on Multiple Known Emitters[J]. Aerospace Electronic Warfare, 2015, 31(3): 1-5. (in Chinese)
[9] 苏成晓, 郭辉, 徐海源, 等. 旋转干涉仪定位体制系统误差标校方法[J]. 航天电子对抗, 2021, 37(3): 28-30.
Sun Chengxiao, Guo Hui, Xu Haiyuan, et al. Calibration Method of Rotating Interferometer Positioning System[J]. Aerospace Electronic Warfare, 2021, 37(3): 28-30. (in Chinese)
[10] 郭福成, 樊昀, 周一宇. 空间电子侦察定位原理[M]. 北京: 国防工业出版社, 2012.
Guo Fucheng, Fan Yun, Zhou Yiyu. Localization Principles in Space Electronic Reconnaissance[M]. Beijing: National Defense Industry Press, 2012. (in Chinese)
[11] 张绍飞, 赵迪. 矩陣论教程[M]. 2版. 北京: 机械工业出版社, 2012.
Zhang Shaofei, Zhao Di. Matrix Theory Tutorial[M]. 2nd ed. Beijing: China Machine Press, 2012. (in Chinese)
Calibration and Emitters Selection Method of Interferometer
Based on Single or Double Emitters
Abstract:The traditional method of joint calibration of fixed baseline interferometer with multiple errors requires more than three calibration emitters to achieve real-time calibration of the interferometer in orbit, but the performance of the traditional method will be reduced or even failed when the number of calibration emitters is insufficient. For the situation that the number of calibration emitters is insufficient, a single or double emitters calibration method for fixed baseline interferometer is proposed. Under the condition of relative motion between the interferometer and the calibration emitters, a set of phase differences of calibration signals is obtained firstly by multiple measurements, and a set of equations about the systematic errors of the interferometer is listed by using the obtained phase differences, finally the systematic errors are solved by the Penrose inverse matrix assisted iterative least squares method. The simulation results verify the feasibility of the proposed method. On this basis, the influence of the emitter selection on the positioning performance of the interferometer after calibration is analyzed qualitatively by means of numerical simulation, decomposing the parameters of the emitter selection. The analysis results show that the calibration emitter located near the sub-star in the single emitter case or two calibration emitters located far apart both can make the interferometer obtain better positioning performance after calibration.
Key words: interferometer; calibration; systematic error; single emitter; double emitters
