基于分数阶自适应神经网络的电动舵机伺服系统摩擦干扰补偿控制
2024-04-18陈渝丰徐晓璐张金鹏张昆峰岳强张文静
陈渝丰 徐晓璐 张金鹏 张昆峰 岳强 张文静
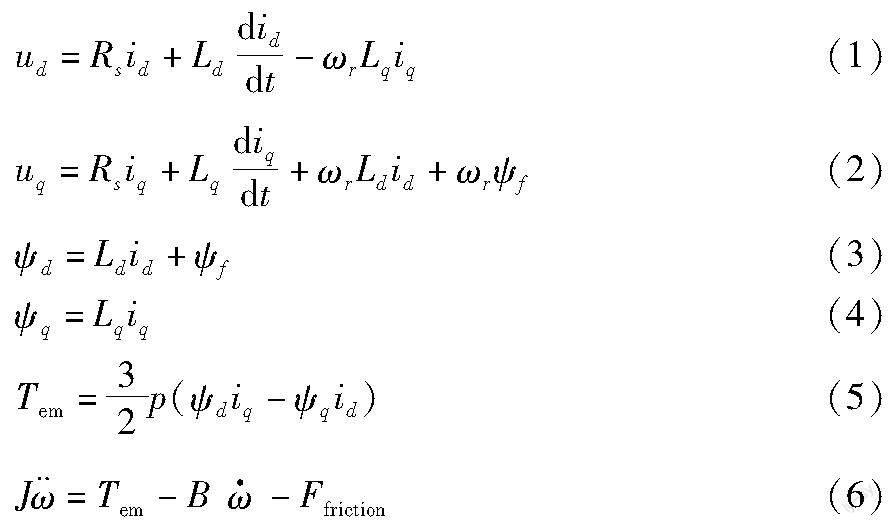
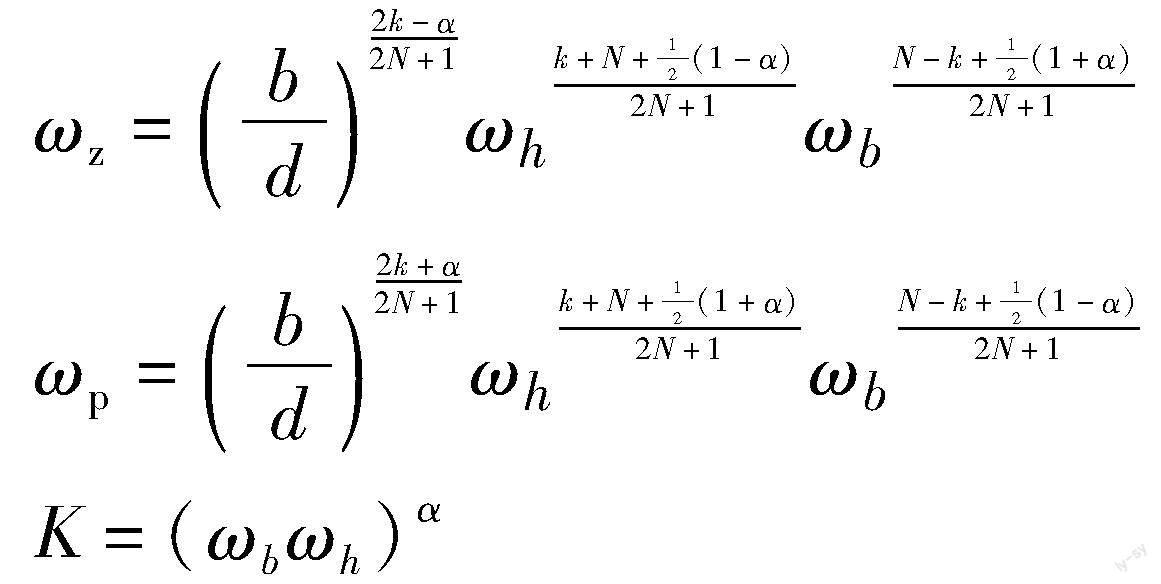
摘 要: 摩擦干扰力矩影响电动舵机伺服系统的跟踪性能, 造成位置和速度跟踪偏差, 甚至可能导致伺服系统不稳定。 针对摩擦力矩干扰下的电动舵机伺服系统跟踪性能差的问题, 本文提出了一种分数阶自适应神经网络摩擦补偿算法(FOANN), 估计并补偿摩擦干扰力矩。 首先, 建立基于LuGre模型的电动舵机伺服系统模型, 利用径向基神经网络估计模型中的不可测状态变量。 其次, 设计FOANN摩擦补偿控制器, 利用李雅普诺夫稳定性理论证明电动舵机闭环系统的稳定性。 最后, 利用仿真和实验平台, 对比分析了FOANN、 传统PD控制和模型自适应控制的性能。 结果表明, 基于本文所提出的FOANN摩擦力矩补偿控制算法, 电动舵机伺服系统的位置跟踪误差和速度跟踪误差均大幅减小, FOANN算法能够有效估计并补偿摩擦力矩, 降低摩擦干扰对电机舵机伺服系统的影响, 提高伺服系统的动态性能。
关键词: 电动舵机; 摩擦; LuGre模型; 分数阶控制; 自适应控制; 径向基神经网络
中图分类号: TJ765
文献标识码: A
文章编号: 1673-5048(2024)01-0133-08
DOI: 10.12132/ISSN.1673-5048.2023.0104
0 引 言
电动舵机是控制导弹飞行轨迹的执行机构, 其性能的优劣决定了导弹的制导精度和快速机动能力[1-2]。 电动舵机伺服系统的跟踪性能受到诸多因素的影响, 其中, 摩擦力矩会造成“抖动”或“爬行”现象, 是导致电动舵机伺服系统跟踪性能降低的重要因素[3-6]。 利用控制方法消除摩擦干扰的影响, 能够提高舵机系统的性能。
近年来, 国内外众多学者对摩擦力矩补偿算法进行了研究, 主要分为无模型摩擦补偿算法和基于模型的摩擦补偿算法两类。 无模型摩擦补偿控制方法将摩擦视为一种扰动, 控制算法实现简单但补偿效果有限[7]。 为了追求更高的控制性能, 需建立摩擦模型来设计摩擦补偿控制方法。 常见的摩擦模型有Stribeck模型、 Karnopp模型、 LuGre模型等。 LuGre模型能够全面精确地反映预滑动位移、 摩擦滞环、 变化的临界摩擦、 爬行以及Stribeck效应等摩擦特性, 得到了广泛应用[8-12]。 基于LuGre模型, 提出了各种不同的先进摩擦补偿控制方法, 如自适应控制[13]、 自适应滑模[14]、 鲁棒自适应[15]以及自适应反步[16]等, 一定程度上降低了摩擦干扰的影响。 随着分数阶控制理论的发展, 分数阶控制算法以其控制精度更高和鲁棒性更强的优点[17-20], 逐渐成为一种重要的控制方法。
本文基于LuGre模型, 利用径向基神经网络估计LuGre模型中的不可测状态变量, 引入分数阶控制理论, 提出一种基于分数阶自适应神经网络(Fractional Order Adaptive Neural Network, FOANN)的电动舵机伺服系统补偿控制方法。 该控制器由四個模块组成: PD、 前馈、 速度反馈以及分数阶神经网络摩擦力矩补偿模块, 并利用李雅普诺夫稳定性理论证明了电动舵机伺服系统稳定性。
该控制方法可以实时估计并补偿系统受到的LuGre摩擦力矩, 从而降低摩擦干扰对系统控制性能的影响, 提高系统跟踪性能。 通过与PD控制器和模型参考自适应控制器(Model Reference Adaptive Control, MRAC)的仿真和实验平台对比实验, 验证了所提控制方法的有效性。
1 基于LuGre模型的电动舵机模型
在两相旋转d-q坐标系下, 基于永磁同步电机(PMSM)的电动舵机伺服系统的动力学模型如下:
式中: ud, uq为d, q轴电压; id, iq为d, q轴电流; ψd, ψq为d, q轴磁链; Ld, Lq为d, q轴电感; Rs为相电阻; ωr为转子角速度; ψf为永磁链; Tem为电磁转矩; p为电机极对数; J为转动惯量; ω为旋转的机械角度; Ffriction为摩擦力矩; B为阻尼系数。
对于电动舵机伺服系统, 为了消除磁场定向控制中产生转矩脉动, 令id=0。 不失一般性, 令Ld=Lq=L, ψd=ψq=ψf。 电动舵机运动方程改写为
令控制器输出u=iq, 电动舵机伺服系统模型改写为
式中: σ0为鬃毛的刚度系数; σ1为阻尼系数; σ2为黏性摩擦系数; v为相对运动速度; vs为Stribeck效应速度; g(v)描述Stribeck现象; Fc为库仑摩擦力; Fs为最大静摩擦力; Ff为LuGre摩擦力矩; z表示鬃毛的平均形变, 为不可测状态变量。
定义参数σ、 (v)如下:
σ=σ1+σ2
将上两式代入式(12), LuGre摩擦力矩可改写为
Ff=σ0z-σ1|v|(v)z+σv(13)
2 基于神经网络的不可测状态变量估计
利用径向基神经网络估计LuGre摩擦力矩中的不可测状态变量z:
z=wTh(i(t))+ε(i(t))(14)
式中: w∈Rp为未知权重向量; i(t)为输入向量; ε(i(t))为有界估计误差; h(i(t))为基向量, h(i(t))=[h0(i(t)), …, hp(i(t))]T∈Rp。
将式(14)代入式(13)中, LuGre摩擦力矩可改写为
Ff=σ0wTh(i(t))-σ1v(v)wTh(i(t))+σv+ε(i(t))(σ0-σ1v(v))(15)
LuGre摩擦力矩的估计误差εf可表示为
εf=ε(i(t))(σ0-σ1v(v))(16)
若速度v有界, 则估计误差εf有上界ε0, 即εf≤ε0。
3 分数阶自适应神经网络补偿控制器设计
为了减小LuGre摩擦力矩干扰对电动舵机伺服系统的不利影响, 基于LuGre模型的电动舵机伺服系统模型和径向基神经网络的不可测状态变量估计, 结合分数阶控制理论, 设计FOANN控制器, 并根据李雅普诺夫稳定性定理, 证明系统稳定性。
3.1 分数阶微积分
分数阶微积分利用分数阶微积分算子, 使得控制系统可调参数增加, 提供更丰富的系统信息, 提高系统控制性能和鲁棒性, 是整数阶微积分的延伸。 分数阶微积分定义种类繁多, 本文选择RL分数阶微积分定义:
RL分数阶积分定义如下:
式中: RaIηt为积分算子; t、 a为积分算子的上、 下限; η为积分阶次。
性质1: 已知微分阶次α=1, 若f(t)为常量, 则在微分区间[a, t]内有RaDαtf(t)=0。
性质2: 若微分阶次α和积分阶次η都为正实数, 则在微分区间[a, t]内有RaDαt[RaIηtf(t)]=RaDα-ηtf(t)。
为了简化分数阶微积分的计算, 提高其实用性, 本文采用改进型Oustaloup算法[21]拟合分数阶微积分, 其在拟合频段[ωb, ωh]内的近似公式为
式中: b, d∈R+; 零点ωz、 极点ωp和增益K分别表示为
3.2 FOANN控制器设计
电动舵机伺服系统误差eω, ev和e定义如下:
eω=ω-ωd(24)
ev=v-vd(25)
e=ev+λeω(26)
神经网络参数ε0的估计误差定义如下:
由于待设计正参数λ>0, 系统的误差传递函数Ge(s)=eω(s)/e(s)=1/(s+λ)始终保持稳定, 因此e和eω具有相同的收敛性。 为减小电动舵机伺服系统摩擦干扰的影响, 以系统误差e尽可能小为控制目标。
根据电动舵机伺服系统模型式(8)~(9)以及LuGre摩擦力矩表达式(15), 设计FOANN控制律如下:
式中: c为待设计的正参数。
FOANN控制器结构框图如图1所示, 主要包括4个
式中: kε、 kσ、 k0、 k1和Υ0、 Υ1分别为待整定的正参数和正定矩阵; α和β分别为待整定的微分阶次和积分阶次。
定理1: 对于LuGre摩擦力矩式(15)干扰下的电动舵机伺服系统式(8)~(9), 利用FOANN控制律式(28)以及参数更新律式(29)~(34), 可以保证系统全局渐进稳定, 且当t→∞时, 系统误差e→0。
证明1: 系统的李雅普诺夫方程V定义如下:
根据性质2, 对李雅普诺夫方程V求导得
将式(8)~(9)、 (15)、 (20)~(21)、 (24)~(28)代入(36)得
根据性质1以及性質3得
将参数更新律式(29)~(34)代入式(38)得
至此, 定理1证明完毕。
4 仿真及实验验证
基于如图2所示的舵机实验平台及其参数, 验证所提出的分数阶自适应神经网络摩擦补偿算法的有效性。 在实验平台中, 利用实时仿真器控制负载电机驱动器, 驱动负载电机, 模拟舵机系统的摩擦干扰。 利用PD控制器以及MRAC控制器和所提出的FOANN控制器进行仿真及实验验证, 电动舵机参数如表1所示。
4.1 控制器参数整定
步骤1: PD控制参数整定
MRAC控制器和FOANN控制器中均包含相同结构的PD控制模块。 选取合适的PD参数, 可以提高系统的动态性能。 参数整定时, 量化性能指标如下:
(1) 无摩擦干扰时, 3种控制器的最大位置误差均小于3%;
(2) 存在基于LuGre模型的摩擦干扰时, MRAC控制器和FOANN控制器的最大位置误差小于6%。
根据上述指标, 选择如下PD参数:
(1) PD控制器参数: kP=2.36×102, kD=6.8。
(2) MRAC控制器的PD控制模块参数: cm=6.1×10-2, km=5.2×101。
(3) FOANN控制器的PD控制模块参数: c=3.15, λ=13。
步骤2: 自适应参数整定
理论上, 自适应参数可以选择任意大于零的值, 但在实际应用中, 自适应参数对系统性能存在如下影响:
(1) 随着kσ和k0增大, 估计参数收敛速度加快, 系统性能提高, 但相应的控制输出波动变大;
综合考虑系统跟踪性能和稳定性, 选择如下的自适应参数:
(1) MRAC控制器的自适应参数: k0,m=2.28×10-3, k1,m=5.04×10-5, kσ,m=5.45×10-3。
(2) FOANN控制器自适应参数: k0=2.2, k1=5.1×10-3, kσ=2.9×10-1。
步骤3: 分数阶参数整定
分数阶参数过小会导致系统对LuGre摩擦力矩的估计速度下降, 过大则会导致估计的LuGre摩擦力矩出现震荡, 甚至过拟合, 导致系统控制精度降低, 稳定性下降。 综合考虑LuGre摩擦力矩估计参数的收敛速度、 控制精度以及系统稳定性, 选择如下的FOANN控制器分数阶参数:
(1) FOANN控制器分数阶神经网络参数: Υ0=1.3·E, Υ1=(9.5×10-1)·E, kε=1×10-4。 E为单位矩阵。
(2) FOANN控制器的分数阶微积分参数: α=0.45, β=0.54。
4.2 仿真结果分析
设置电动舵机位置伺服系统的采样时间为10-4 s, 运行时间为10 s, 期望位置轨迹ωd(t)=sin(2πt)。
图3~4分别给出了3种控制器的位置跟踪曲线和位置跟踪误差曲线。 由图可知, PD控制器的位置跟踪曲线出现了明显的“平顶”现象, 未能准确跟踪输入信号, 最大位置跟踪误差为1.19×10-1 rad; MRAC控制器在一定程度上补偿了摩擦力矩, 改善了“平顶”现象, 最大位置跟踪误差为2.59×10-2 rad; FOANN控制器更准确地估计并补偿了LuGre摩擦力矩, 大幅削弱了“平顶”现象, 最大位置跟踪误差仅为2.85×10-3 rad, 低于PD控制器两个数量级, 低于MRAC控制器一个数量级。 最大位置跟踪误差如表2所示。
图5~6分别给出了3种控制器的速度跟踪曲线和速度跟踪误差曲线。 由图可知, PD控制器没有補偿LuGre摩擦力矩, 其速度跟踪轨迹零点的邻域附近出现了明显的“死区”现象, 最大速度跟踪误差为1.38 rad/s;MRAC控制器在一定程度上补偿了LuGre摩擦力矩, 改善了“死区”现象, 最大速度跟踪误差为1.23 rad/s, 误差略小于PD控制器; FOANN控制器更准确地估计并补偿了LuGre摩擦力矩, 大幅削弱了“死区”现象, 最大速度跟踪误差仅为6.22×10-2 rad/s, 低于PD控制器和MRAC控制器两个数量级。 最大速度跟踪误差如表2所示。
图7比较了给定LuGre摩擦力矩与MRAC控制器以及FOANN控制器所估计的LuGre摩擦力矩。 由图可知, MRAC控制器估计LuGre摩擦力矩与给定LuGre摩擦力矩之间存在较大误差; FOANN控制器估计的LuGre摩擦力矩与给定LuGre摩擦力矩之间存在微小误差, 估计准确性较高。
3种控制器的控制输出如图8所示。 由图可知, FOANN控制器的控制输出曲线平滑, 没有明显的抖动。 虽然FOANN控制器需要提供额外的补偿控制输出来补偿LuGre摩擦力矩, 但其控制输出与PD控制器和MRAC控制器近似相同。
4.3 实验结果分析
为了进一步验证分数阶自适应神经网络补偿控制方法的有效性, 基于图2所示的实验平台, 采用与仿真相同的控制器参数, 对比分析PD控制器、 MRAC控制器以及本文所提出的FOANN控制器的控制性能。
图9~10分别给出了3种控制器的实验平台位置跟踪曲线及其误差曲线, 表3给出了3种控制器的最大位置跟踪误差。 可以看出, 相比仿真结果, 3种控制器的位置跟踪性能均有所下降, 但FOANN控制器的性能仍然优于PD控制器和MRAC控制器。
图11~12分别给出了3种控制器的实验平台速度跟踪曲线及其误差曲线, 表3给出了三种控制器的最大速度跟踪误差。 可以看出, 在速度跟踪轨迹零点的邻域附近, 3种控制器作用下的电动舵机伺服系统速度跟踪曲线均出现了波动, MRAC控制器和PD控制器的波动幅度较大, 但FOANN控制器的波动不明显。 实验结果表明, FOANN能够有效改善“死区”现象, 速度跟踪更平稳, 精度更高。
MRAC控制器和FOANN控制器的实验平台LuGre摩擦力矩估计曲线如图13所示。 可以看出, 相较于MRAC控制器, FOANN控制器对LuGre摩擦力矩的估计更平稳, 抖动更小, 虽相比于仿真时震荡略大, 但仍能较好地估计摩擦力矩。
综合以上仿真和实验结果可知, 相比于PD控制器和MRAC控制器, FOANN控制器更准确实时地估计并补偿电动舵机位置伺服系统的LuGre摩擦力矩, 以微小的额外控制输出, 可以实现更好的控制效果。
5 结 论
针对电动舵机伺服系统中的摩擦干扰问题, 本文基于LuGre模型, 利用径向基神经网络估计了系统模型中的不可测状态变量, 设计了分数阶自适应神经网络摩擦补偿控制器。 该控制器由PD、 前馈、 速度反馈和分数阶自适应神经网络摩擦力矩补偿四个模块组成, 并利用李雅普诺夫稳定性理论证明了系统稳定性。 与PD控制器和MRAC控制器的对比仿真和实验结果表明, FOANN控制器以微小的额外控制输出, 更准确实时地估计并补偿了舵机伺服系统受到的摩擦力矩, 使舵机伺服系统跟踪性能显著提高。
参考文献:
[1] 王婷, 张昆峰, 武飞. 基于模型的舵机非线性因素补偿控制研究[J]. 航空兵器, 2018(2): 34-37.
Wang Ting, Zhang Kunfeng, Wu Fei. Study of Model-Based Nonlinear Compensate Control for the Servo System[J]. Aero Weaponry, 2018(2): 34-37. (in Chinese)
[2] 梁建, 王春艳, 段丽华, 等. 电动舵机刚柔耦合动力学仿真研究[J]. 航空兵器, 2019, 26(5): 77-82.
Liang Jian, Wang Chunyan, Duan Lihua, et al. Rigid-Flexible Coupling Kinetic Simulation Study on the Electromechanical Actuator[J]. Aero Weaponry, 2019, 26(5): 77-82.(in Chinese)
[3] 杨尧, 赵岳楼, 闫杰. 高超声速飞行器舵机摩擦的影响及其抑制方法[J]. 指挥控制与仿真, 2014, 36(2): 85-87.
Yang Yao, Zhao Yuelou, Yan Jie. Effection and Restrained of Acutaor Friction on Hypersonic Vehicle[J]. Command Control & Simulation, 2014, 36(2): 85-87.(in Chinese)
[4] 彭书华, 李华德, 苏中. 非线性摩擦干扰下的电动舵机滑模变结构控制[J]. 信息与控制, 2008, 37(5): 637-640.
Peng Shuhua, Li Huade, Su Zhong. Sliding Mode Variable Structure Control for Electromechanical Actuator with Nonlinear Friction[J]. Information and Control, 2008, 37(5): 637-640.(in Chinese)
[5] 李冬輝, 王立献, 周满, 等. 基于改进径向基网络的电动舵机滑模控制[J]. 兵器装备工程学报, 2023, 44(4): 217-223.
Li Donghui, Wang Lixian, Zhou Man, et al. Sliding Mode Control of Electromechanical Actuators Based on an Improved RBF Network[J]. Journal of Ordnance Equipment Engineering, 2023, 44(4): 217-223.(in Chinese)
[6] 卢晋, 吴志刚, 杨超. 电动舵机模块化建模及动刚度仿真[J]. 北京航空航天大学学报, 2021, 47(4): 765-778.
Lu Jin, Wu Zhigang, Yang Chao. Modular Modeling and Dynamic Stiffness Simulation of Electromechanical Actuator[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(4): 765-778.(in Chinese)
[7] Kang M S. Robust Digital Friction Compensation[J]. Control Engineering Practice, 1998, 6(3): 359-367.
[8] Simoni L, Beschi M, Visioli A, et al. Inclusion of the Dwell Time Effect in the LuGre Friction Model[J]. Mechatronics, 2020, 66: 102345.
[9] Capace A, Cosentino C, Abidi H, et al. Modelling and Identification of the Asymmetric Hysteresis in the Viscoelastic Response of the Fingertip under Indentation: A Multistate Friction Model with Switching Parameters[J]. Mechatronics, 2021, 77: 102578.
[10] Sun Y H, Chen T, Wu C Q, et al. A Comprehensive Experimental Setup for Identification of Friction Model Parameters[J]. Mechanism and Machine Theory, 2016, 100: 338-357.
[11] Marques F, Woliński L, Wojtyra M, et al. An Investigation of a Novel LuGre-Based Friction Force Model[J]. Mechanism and Machine Theory, 2021, 166: 104493.
[12] Hieu N N, Chung P N. Analysis of Stability and Stick-Slip Motion of a Friction-Induced Vibrating System with Dwell-Time Effect[J]. International Journal of Mechanical Sciences, 2021, 205: 106605.
[13] Yao J Y, Deng W X, Jiao Z X. Adaptive Control of Hydraulic Actuators with LuGre Model-Based Friction Compensation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6469-6477.
[14] 谭文斌, 李醒飞, 裘祖荣, 等. 基于改进型LuGre模型的自适应滑模摩擦补偿方法[J]. 天津大学学报: 自然科学与工程技术版, 2015, 48(5): 463-467.
Tan Wenbin, Li Xingfei, Qiu Zurong, et al. Adaptive Sliding Friction Compensation Method Based on Modified LuGre Model[J]. Journal of Tianjin University: Science and Technology, 2015, 48(5): 463-467.(in Chinese)
[15] 殷婷婷, 贾方秀, 于纪言, 等. 基于改进LuGre摩擦模型的双旋弹丸固定舵翼滚转位置鲁棒自适应控制算法[J]. 兵工学报, 2019, 40(12): 2425-2432.
Yin Tingting, Jia Fangxiu, Yu Jiyan, et al. Robust Adaptive Control of Roll Position of Fixed Rudder for Dual-Spin Projectile with Improved LuGre Friction Model[J]. Acta Armamentarii, 2019, 40(12): 2425-2432.(in Chinese)
[16] Ahmed F S, Laghrouche S, Harmouche M. Adaptive Backstepping Output Feedback Control of DC Motor Actuator with Friction and Load Uncertainty Compensation[J]. International Journal of Robust and Nonlinear Control, 2015, 25(13): 1967-1992.
[17] 管萍, 罗宗樾, 戈新生. 基于RBF神经网络的挠性航天器分数阶滑模姿态控制[J]. 飞行力学, 2021, 39(6): 68-74.
Guan Ping, Luo Zongyue, Ge Xinsheng. Fractional Order Sliding Mode Attitude Control of Flexible Spacecraft Based on RBF Neural Network[J]. Flight Dynamics, 2021, 39(6): 68-74.(in Chinese)
[18] Wang T H, Zhao X M, Jin H Y. Robust Tracking Control for Permanent Magnet Linear Servo System Using Intelligent Fractional-Order Backstepping Control[J]. Electrical Engineering, 2021, 103(3): 1555-1567.
[19] Sun G H, Wu L G, Kuang Z A, et al. Practical Tracking Control of Linear Motor via Fractional-Order Sliding Mode[J]. Automa-tica, 2018, 94: 221-235.
[20] Sun G H, Ma Z Q. Practical Tracking Control of Linear Motor with Adaptive Fractional Order Terminal Sliding Mode Control[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(6): 2643-2653.
[21] 齊乃明, 秦昌茂, 王威. 分数阶系统的最优Oustaloup数字实现算法[J]. 控制与决策, 2010, 25(10): 1598-1600.
Qi Naiming, Qin Changmao, Wang Wei. Optimal Oustaloup Digi-tal Realization of Fractional Order Systems[J]. Control and Decision, 2010, 25(10): 1598-1600.(in Chinese)
A Friction Disturbance Compensation Method for Electromechanical
Actuator
Based on Fractional Order Adaptive Neural Network
Abstract:Friction torque disturbance affects the tracking performance of electromechanical actuator servo system, bringing position and speed tracking errors, and even may leading to instability of the servo system. Aiming at the problem of poor tracking performance of electromechanical actuator servo system under friction torque disturbance, a FOANN friction compensation algorithm is proposed to estimate and compensate the friction torque. Firstly, base on LuGre friction model, a electromechanical actuator model is established, and the unmeasured state variable in the LuGre model is estimated by radial basis function neural network. Secondly, a FOANN controller is designed, and the stability of corresponding closed-loop system is proved by Lyapunov stability theory. Finally, through simulation and experimental platform, the dynamic performance of FOANN is compared with those of traditional PD and MRAC. The simulation and experimental results show that, with the proposed FOANN friction torque compensation algorithm, the tracking errors of both position and velocity of electromechanical actuator servo system are greatly reduced. FOANN algorithm can effectively estimate and compensate friction torque, reduce the impact of friction disturbance and enhance the dynamic performance of the servo system.
Key words: electromechanical actuator; friction; LuGre model; fractional order control; adaptive control; radial basis function neural network
