干涉仪对频分正交MIMO雷达的测向性能分析
2024-04-18冯一伦蒋彦雯曾桂兰范红旗
冯一伦 蒋彦雯 曾桂兰 范红旗

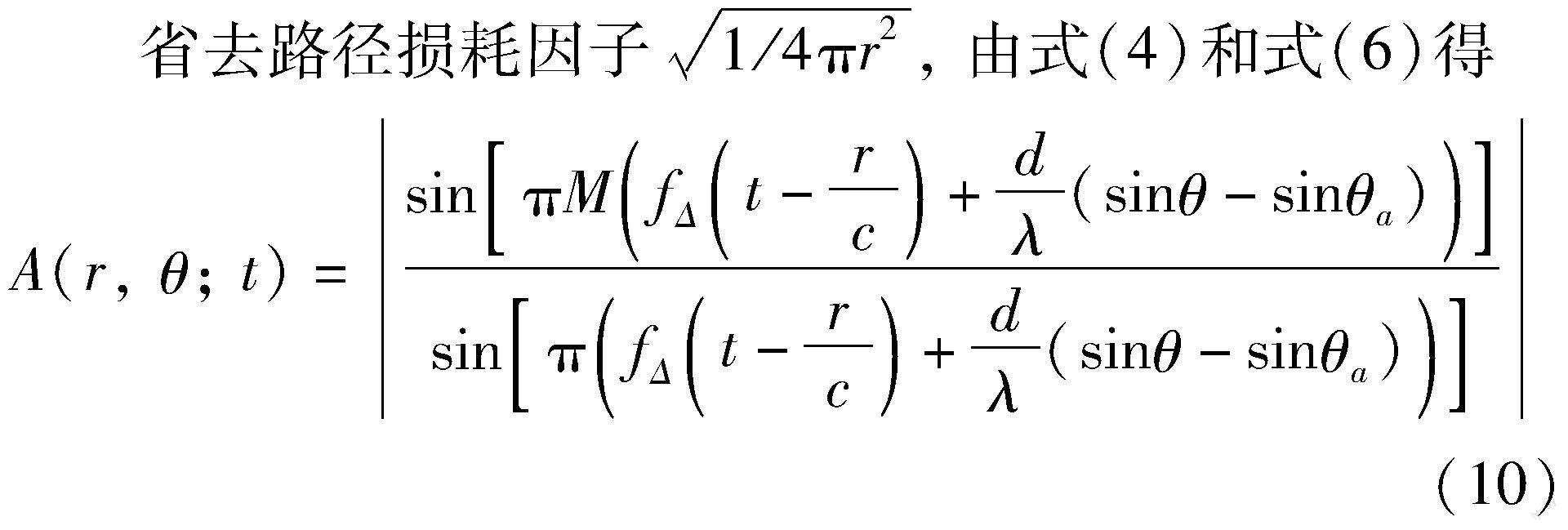

摘 要: 频分正交MIMO雷达的空间合成信号脉冲具有时变包络和空时耦合特性, 为主动对抗无源电子侦察系统的测向提供了新的可能。 本文针对相位干涉仪测向系统分析了电子侦察系统对频分正交MIMO雷达的测向误差。 首先建立远场侦察接收机MIMO雷达合成信号模型, 分析其时变包络特性和相位波前畸变特性及其对测向性能的影响, 并提出一种通过初相调制来增大干涉仪测向误差的可行路径。 仿真结果表明, 相位波前畸变区和瞬时信噪比影响的干涉仪DOA估计误差主导性区域不同。 利用MIMO雷达阵元相位调制可操控包络起伏特性, 改变合成信号峰均比(PAR)从而增大抗截获性能。 在干涉仪分析窗内, 与相控阵雷达合成信号相比, 当侦察接收机先验位置已知时, MIMO雷达合成信号功率可下降25 dB左右, 而距离未知时也可下降10 dB左右, 因此MIMO雷达能在一定程度上增大干涉仪的测向误差。
关键词: MIMO雷達; 相位调制; 相位波前畸变; 相位干涉仪; 测向误差
中图分类号: TJ760; TN958
文献标识码: A
文章编号: 1673-5048(2024)01-0103-08
DOI: 10.12132/ISSN.1673-5048.2022.0207
0 引 言
现代战争中, 制电磁权的核心就是侦察与反侦察的对抗, 随着电子战技术的发展, 雷达的生存面临巨大的威胁。 雷达对抗侦察技术一般分为两种, 一种是防御性的, 即通过功率管理、 频率捷变、 复杂调制、 大带宽等低截获概率(LPI)技术使得非合作侦察接收机对信号的检测、 识别和参数估计变得困难; 另一种是主动性的, 即设置干扰源实施噪声干扰, 或者发射与雷达信号相似的假辐射源信号, 从而掩护己方雷达信号[1–3]。 近年来, 一种具备干扰、 侦察、 定位等多种功能的微型空射诱饵(MALD)快速发展, 战时可由防区外电子战飞机发射进入对方防空区域抵近侦察[4], 雷达信号将不可避免被截获。 由于辐射源到达角是侦察系统信号分选和定位的一个重要参数, 而准确定位则是进一步完成电子软硬杀伤的前提, 如果能有效降低电子侦察系统的测向精度, 必然能提升我方雷达的战场生存能力。
MIMO雷达是一种新体制雷达, 各阵元可同时发射不同波形, 具有较高的设计自由度, 从主动对抗侦察机的角度看, 在MIMO雷达信号特性层面展开分析, 研究空间合成信号对电子侦察系统测向定位的误差影响, 进而通过波形设计和相位调制的方式增大电子侦察系统的测向定位误差, 同时不影响己方雷达探测性能, 具有一定的可行性。 现阶段, 主动对抗无源定位系统的研究主要是利用相干干扰进行的[5–8], 通过雷达波形本身的辐射特性主动对抗电子侦察系统测向定位的研究较少。 文献[9–12]主要研究了侦察机对具有较小频偏的频控阵雷达的测向定位误差, 表明阵列雷达可以通过不同频控函数有效增大定位误差。 文献[13]研究了OFDM-MIMO雷达信号的反侦察性能, 分析了MIMO雷达的脉内信号时变特性对侦察机测向的影响。 文献[14-15]研究了MIMO雷达信号抗到达时差定位的效果, 表明MIMO雷达的反定位效果要优于相控阵雷达。 然而, 这些研究并没有深入研究MIMO雷达发射加权参数对侦察机测向欺骗的影响效果, 未考虑多阵元信号空间合成信号的相位波前畸变特性。
一般的测向方法主要针对单载频恒包络脉冲信号, 但频分正交MIMO雷达远场合成信号将具有时变包络特性和相位波前畸变特性, 这一特性将影响电子侦察系统对MIMO雷达信号DOA参数的测量结果。 因此, 本文以干涉仪对频分正交MIMO雷达DOA测量为例, 在发射信号能量约束下建立MIMO雷达远场合成信号及其幅度和相位的空时分布模型, 在此基础上进一步分析DOA测量误差规律以及通过MIMO雷达信号初相调制增大相位干涉仪测向误差的可能性。
1 MIMO雷达信号模型
MIMO雷达的每个阵元发射相互正交的信号, 不失一般性, 考虑由M个偶极子天线构成的MIMO雷达系统。 其一维均匀线阵(Uniform Linear Array, ULA)结构如图1所示, 图中, s1, s2, …, sM为各阵元的发射信号; d为阵元间距。
第m个阵元信号可表示为
发射信号之间满足
式中: TP为脉冲宽度; Es为信号能量。
以MIMO雷达为坐标原点, 考虑在雷达天线远区(即r≥2D2/λ, D为雷达孔径, λ为雷达波长), 波阵面局部可用平面波表示。 在窄带条件下, MIMO雷达阵列孔径渡越时间远小于MIMO信号带宽的倒数, 因此可忽略不同阵元发射信号的包络延迟差异及其带来的附加相位差, 此时, 观测点(r, θ)处的MIMO雷达远场合成信号可表示为
式中: wm是第m个阵元的初相控制系数。
采用欧拉公式法[16], 可得MIMO雷达远场合成信号的幅度分布函数和相位分布函数, 即
令每个阵元的信号功率为Pt=Es/TP, 归一化距离衰减因子后, 由式(1)~(3)可得, MIMO雷达信号的空间平均功率分布为
由式(7)可知, 正交MIMO雷达信号的空间平均功率不随角度变化, 表现为宽波束。
当各阵元的发射信号完全相同时, 即s1=s2=…=sM, 此时对应相控阵雷达的工作模式, 代入式(7)可得相控阵雷达平均辐射功率的空间分布:
由式(8)可知, 相控阵雷达发射的是高增益的窄波束, 其平均辐射功率是关于角度的函数。
2 频分正交MIMO雷达合成信号空时分布特性
MIMO雷达的正交波形可以从时域、 频域或码域上设计[17]。 本文考虑线性频分正交MIMO雷达信号, 即将同一信号包络调制到等间隔载频上的一组正交信号。 为简化分析, 考虑矩形包络脉冲, 记参考阵元的信号载频为fc, 相邻阵元的信号频差为fΔ(为了保证正交性, fΔ应为1/TP的整数倍)。 初相控制系数wm一般可取任意相位调制序列或如式(9)所示的相位系数。
式中: θa为参数, 类似相控阵雷达的波束扫描控制角。
2.1 频分正交MIMO雷达合成信号幅度特性
由式(10)可知, 频分正交MIMO雷达的幅度分布为辛克函数形状, 且具有时变特性。 进一步可得归一化的脉内峰值位置:
由式(11)可知, 幅度峰值的相对周期为1/fΔTP。 当fΔTP=1时, 幅度分布函数只有一个峰值。 通過参数θa可以灵活调控峰值位置, 例如, 需要将峰值置于信号中部, 令tpeak/TP=1/2便可解出所需的控制参数θa。
当MIMO雷达处于相控阵工作模式时, 即fΔ=0 Hz, 代入式(10)可得相控阵雷达远场合成信号的幅度分布:
由式(12)可知, 相控阵雷达的远场信号幅度只与观测角度有关, 且不同于正交MIMO雷达全向发射的工作方式, 相控阵雷达的发射波束需要通过相位控制实现角度扫描。 另外, 与式(10)对比可知, 由于式(12)中与时间参量t无关, 因此相控阵雷达远场合成信号脉冲包络表现为恒包络特性。
2.2 频分正交MIMO雷达合成信号相位特性
由式(5)和式(6)可得, 频分正交MIMO雷达合成信号的相位分布函数为
等相位面是某一时刻空间中相位相等点构成的平面。 类似于相干多点源干扰对抗单脉冲测角的原理。 多阵元矢量合成信号能够使等相位面在某点发生较大的畸变[18-19], 称为相位波前畸变现象。 相位梯度垂直于等相位面, 其定义式为
式中: r和θ分别表示距离维和角度维的方向单位矢量。
由于相位干涉仪实际测量的是相位梯度的方向。 按照相位梯度法的基本原理[20], 考虑位于平面内距离MIMO雷达任意一点r, θ处, 可用该处的相位梯度矢量与距离矢量的夹角表征该点的相位波前畸变程度。 因此, 定义相位梯度偏差角eθ为
图2给出了相位波前畸变以及相位梯度偏差角的示意图。 当eθ不为0时, 表示相位梯度不平行于距离方向(入射方向)矢量, 即发生了相位波前畸变。 将式(13)代入式(15), 可得
式(16)表明, 频分正交MIMO雷达存在相位波前畸变现象, 其相位梯度偏差角大小与阵元间距d、 阵元数M、 观测点角度θ呈正相关, 与fΔ/fc以及观测点距离r呈负相关。
需要注意的是, 当MIMO雷达处于相控阵工作模式且波束扫描角为θa时, 相控阵雷达的空间相位分布函数为
将式(17)代入式(15), 得
对比式(16)和式(18)可知, 由于式(16)多了fΔ/fc项, 因此频分正交MIMO雷达的相位梯度偏差角小于相控阵雷达。
3 干涉仪对频分正交MIMO雷达的测向误差
3.1 干涉仪测向原理
机载无源侦察系统通常采用相位干涉仪法来估计辐射源DOA。 如图3所示, 相位干涉仪的基本结构具有2个天线, 其中l为干涉仪基线长度。
与干涉仪阵元输出相连的窄带接收信道, 其采样输出可表示为
式中: r=2πlsinα/λ是附加相移; x[n]是干涉仪处MIMO雷达合成信号的离散采样序列; v1[n]和v2[n]是均值为零、 方差为σ2n的加性高斯白噪声序列。
通过两接收信号内积可以得到归一化正交相位差信号, 即
则相位差序列为
3.2 干涉仪测向误差分析
对式(22)全变量微分, 可得
做变量代换λ=c/f。 假设干涉仪基线长度误差dl=0, 其他误差源相互独立, 由误差传递公式可得
当电子侦察系统对辐射源信号的采样点数为L时, 双阵元干涉仪的联合接收矢量可写为
对于高频窄带信号, 相对测频误差σf/f的值很小, 可忽略不计, 把式(26)代入式(24), 得到DOA估计的CRLB为
式(27)表明, 在加性高斯白噪声背景下, 干涉仪DOA估计的CRLB与接收信噪比η、 信号采样点数L、 干涉仪基线长度l呈负相关关系, 与信号波长λ和真实到达角α呈正相关关系。
4 仿真实验分析
由理论分析可知, 干涉仪对频分正交MIMO雷达的测向误差源主要包括两部分: (1)相位波前畸变的影响。 由于干涉仪实际上测量的是相位梯度的方向, 频分正交MIMO雷达的相位波前畸变导致相位梯度出现偏差角, 从而增大干涉仪测向误差。 (2)瞬时信噪比的影响。 频分正交MIMO雷达合成信号的时变包络特性会造成干涉仪接收信号瞬时信噪比的起伏, 从而增大测向误差。
注意到控制参数θa可以调控包络峰值位置。 考虑到电子侦察系统在截获辐射源信号后, 为了满足实时测量要求, 通常会截取一段时长的信号进行分析, 如现代宽带侦察接收机一般截取脉冲前沿的一小段时间TΔ进行参数估计。 因此, 通过调整脉冲包络峰值的位置, 可调节并改变侦察接收机分析时段内合成信号的信噪比, 从而增大干涉仪的测向误差。
通过仿真实验分析频分正交MIMO雷达对相位干涉仪DOA测量误差的影响。 仿真实验以地面防空雷达对抗双阵元干涉仪测向的MALD为例。 考虑MALD头锥部尺寸在分米级, L波段MIMO雷达的阵列孔径通常在米级, 因此, 仿真实验MIMO雷达和MALD测向接收机的典型参数设置如表1和表2所示。
4.1 信号空时分布规律
根据式(10)、 (12)、 (13)和(17), 令控制参数θa=0°, 距离r在3~6 km内取值, 分别绘制频分正交MIMO雷达和相控阵雷达空间合成信号的空时幅度分布(去载频), 结果如图4所示。 由图可见: 相比于相控阵雷达脉冲的恒包络和幅度的距离-角度非耦合空变特性, 频分正交MIMO雷达合成脉冲的包络时变且脉内峰值位置呈距离-角度耦合的空变特性, 这是因为频分正交MIMO雷达使用线性等间隔频率而导致的规律性变化; 对比式(13)和(17)可知, 频分正交MIMO雷达和相控阵雷达脉冲前沿(t=r/c)相位的空间一致, 图4(c)和(d)印证了这一结论, 但距离r给定后, 去载频后频分正交MIMO的脉内相位与相控阵雷达有所不同, 同样呈现出时变特性, 图4(c)说明了这一点。
为进一步分析相位波前畸变的影响, 图5(a)给出了频分正交MIMO雷达相位梯度偏差角的空间分布情况, 图5(b)则给出了其与相控阵工作模式下相位梯度偏差角的差异。 由图可见, 频分正交MIMO雷达的相位梯度偏差角随着距离增大而迅速减小, 且小于相控阵工作模式雷达, 但随距离增大, 两者的差异趋近于零。
4.2 干涉仪DOA估计误差影响因素及规律
在表1和表2的典型条件下, 固定侦察接收机的检测灵敏度为3 dB, 检测模式为脉冲前沿检测, 参数估计的分析时长TΔ=1 μs。 通过实验来分析不同阵元数和不同阵元频率间隔对干涉仪DOA估计误差的影响及两种误差源的主导性区间。
图6给出了不同阵元参数下相位梯度偏差角随距离变化情况。 如图6(a)所示, 阵元数越多, MIMO雷达阵列孔径尺寸越大, 干涉仪DOA估计的偏差角就越大。 由图6(b)可知, 阵元频率间隔(等于1/TP的整数倍)对相位波前畸变的影响不大, 在一定距离范围内可以忽略。
图7给出了一种典型条件下(侦察机位于MIMO雷达阵面正前方, 即θ=0°), 两种误差源对相位干涉仪DOA估计误差的影响。 图中, 相位波前畸变占主导作用的范围约3 km以内, 而瞬时信噪比主要影响3 km以外的远距范围。 在相位波前畸变主导区域, 干涉仪对相控阵雷达的DOA估计误差略大于MIMO雷达; 在进入瞬时信噪比主导区域后, 干涉仪对MIMO雷达的DOA估计误差明显大于相控阵雷达, 这与上述分析一致。
4.3 不同初相调制对干涉仪DOA估计误差的影响
本节比较不同初相调制对干涉仪DOA估计的影响。 在式(9)所给出的初相控制系数中, 当θa=θ时, 初相控制系数等于阵列导向矢量, 此时为空间匹配的情况; 当θa≠θ时, 为空间失配情况, 这里考虑θa=90°; 除此之外, 还考虑随机初相控制系数以及相控阵工作模式。 几种情形下初相控制系数的具体设置如表3所示, 实验中, DOA真值设为0°, 干涉仪测量分析窗口为脉冲前沿1 μs的信号。
图8仿真了典型条件下3~6 km的空间中, 不同初相调制方式下频分正交MIMO雷达以及相控阵雷达幅度的空时分布。 需要指出的是, 图8结果中考虑了距离平方衰减因子。
尽管空间匹配、 空间失配、 随机初相3种情形下的频分正交MIMO雷达信号具有相同的平均功率(初相调制不改变正交MIMO雷达信号的平均功率), 但由图8(a)~(c)可见, 不同的初相调制方式不仅可以改变MIMO雷达合成脉冲的峰均比(Peak-to-Average Ratio, PAR), 从而影响侦察接收机对MIMO雷达的截获距离, 而且还通过改变脉冲峰值位置有效调控侦察机分析窗口内的平均信号功率, 从而改变干涉仪SNR并影响DOA估计精度。 对比图8(a)~(c), 图8(d)中相控阵雷达只存在距离衰减, 其在给定距离处的合成信号呈现恒包络特性。
为了更清楚地展示合成脉冲信号包络时变特性的差异, 图9给出了四种配置下距离为3 km处的时域脉冲包络。 由该图可见, 虽然空间匹配和空间失配两种配置下MIMO雷达的脉冲包络与相控阵工作模式具有相同的峰值, 但MIMO雷达的脉冲包络表现出随θa变化的时间循环移位特性。 利用这一点, 可有效降低已知距离处干涉仪分析窗口内的信噪比, 本例取θa=90°时恰好可令频分正交MIMO雷达合成信号包络的最小副瓣位于干涉仪的分析窗内, 从而使干涉仪分析窗内的接收信噪比最低。 此外, 相比其他三种配置, 随机相位配置下频分正交MIMO雷达具有最小的PAR, 这可用于降低未知距离处干涉仪分析窗内的信噪比及反截获应用。
表4进一步计算了图8所示的四种配置下合成信号的PAR以及干涉仪分析窗内的平均功率。 由结果可知: 在相同平均功率下, 随机初相调制的PAR较空间匹配和空间失配下约降低了6.43 dB; 相控阵雷达虽然具有最小的PAR(PAR=1, 恒包絡特性), 但因其平均功率最大, 因此抗截获性能最差; 当干涉仪的距离精确已知时, 本例r=3 km, 通过改变θa可使干涉仪分析窗内的平均信号功率相对于相控阵模式最大下降25.84 dB, 从而显著增大干涉仪的DOA估计误差; 当干涉仪距离不确切时, 本例考虑3~6 km距离范围, 三种配置下干涉仪分析窗内信号平均功率相对相控阵模式分别降低9.03 dB, 11.94 dB和11.4 dB, 能够在一定程度上增大干涉仪DOA估计误差。
5 结 论
频分正交MIMO雷达的合成信号具有时变包络特性和相位波前畸变特性, 这使得干涉仪接收信号的瞬时信噪比出现起伏并出现测角偏差。 本文首先建立了ULA阵列结构MIMO雷达信号模型, 然后推导了采用频分正交波形时MIMO雷达远场合成信号幅度和相位的空间分布, 继而分析了相位波前畸变和脉内信噪比这两种影响干涉仪测角的误差源。 仿真实验发现, 通过调控频分正交MIMO雷达初相控制系数, 可有效增大干涉仪对雷达的DOA估计误差。
研究結果表明, 相位波前畸变和瞬时信噪比对干涉仪DOA估计误差主导性区域分别位于近距区和远距区, 在近距区分析干涉仪对MIMO雷达测向时, 需要考虑频分正交MIMO雷达相位偏差角引入的误差。 对比相同功率孔径的相控阵雷达, 通过调控θa或者采用随机相位控制系数, 可使频分正交MIMO雷达在不同的侦察接收机先验位置信息下显著增大干涉仪测向误差。 因此, 结合典型场景, 深入开展不同信息模式下频分正交MIMO雷达初相自适应调控反侦察和反定位方法及其性能评估, 可作为下一步的研究重点。
参考文献:
[1] 黄鹏刚. 低截获概率雷达技术研究[J]. 现代电子技术, 2003, 26(18): 24-25.
Huang Penggang. Analysis of Low-Probility-of-Intercept Radar Technology[J]. Modern Electronic Technique, 2003, 26(18): 24-25.(in Chinese)
[2] 江桥, 侯庆禹, 黄和国. 舰载雷达主动反电子侦察技术[J]. 航天电子对抗, 2016, 32(1): 52-55.
Jiang Qiao, Hou Qingyu, Huang Heguo. Active CESM Techniques of Shipborne Radar[J]. Aerospace Electronic Warfare, 2016, 32(1): 52-55.(in Chinese)
[3] 林钰, 余强, 毕大平. 雷达反空间电子侦察的干扰方法研究[J]. 舰船电子对抗, 2014, 37(3): 7-11.
Lin Yu, Yu Qiang, Bi Daping. Research into the Jamming Methods of Radar Anti-Electronic Reconnaissance in Space Area[J]. Shipboard Electronic Countermeasure, 2014, 37(3): 7-11.(in Chinese)
[4] 尹航, 郭谡, 温超然, 等. 美微型空射诱饵武器发展分析与应对策略[J]. 空天防御, 2019, 2(3): 84-90.
Yin Hang, Guo Su, Wen Chaoran, et al. Analysis of Development of US MALD and Coping Strategies[J]. Air & Space Defense, 2019, 2(3): 84-90.(in Chinese)
[5] 陈慧, 李昊. 对时差无源定位系统的相干干扰技术[J]. 舰船电子对抗, 2019, 42(5): 1-5.
Chen Hui, Li Hao. Coherent Jamming Technology to Passive TDOA Location System[J]. Shipboard Electronic Countermeasure, 2019, 42(5): 1-5.(in Chinese)
[6] 刘伟, 付永庆, 许达. 二维相位干涉仪在相干干扰下的测向误差模型[J]. 中南大学学报:自然科学版, 2015, 46(4): 1274-1280.
Liu Wei, Fu Yongqing, Xu Da. Direction-Finding Error Model of Two-Dimensional Phase Interferometer under Coherent Interference[J]. Journal of Central South University: Science and Technology, 2015, 46(4): 1274-1280.(in Chinese)
[7] 王诗蕾. 基于预处理的无源定位对抗技术研究[D]. 成都: 电子科技大学, 2016.
Wang Shilei. Research on Preprocessing-Based Locating Countermeasures Technology for Passive Locating System[D]. Chengdu: University of Electronic Science and Technology of China, 2016. (in Chinese)
[8] 曾小东. 远距支援干扰对测向的性能影响分析[J]. 电子信息对抗技术, 2022, 37(2): 18-20.
Zeng Xiaodong. The Influence of Stand-off Jamming on Direction Finding[J]. Electronic Information Warfare Technology, 2022, 37(2): 18-20.(in Chinese)
[9] 關浩亮, 张顺生, 王文钦. 基于频控阵的无源定位对抗技术[J]. 雷达学报, 2021, 10(6): 833-841.
Guan Haoliang, Zhang Shunsheng, Wang Wenqin. Passive Localization Countermeasure Based on Frequency Diverse Array[J]. Journal of Radars, 2021, 10(6): 833-841.(in Chinese)
[10] 王博, 谢军伟, 葛佳昂, 等. FDA对测向时差组合定位的欺骗研究[J]. 空军工程大学学报: 自然科学版, 2019, 20(6): 72-78.
Wang Bo, Xie Junwei, Ge Jiaang, et al. Research on Deception Based on Direction Finding Time Difference Positioning System of FDA[J]. Journal of Air Force Engineering University: Natural Science Edition, 2019, 20(6): 72-78.(in Chinese)
[11] 陈楚舒, 盛川, 谢军伟, 等. 非线性频偏FDA对测向系统的欺骗研究[J]. 空军工程大学学报: 自然科学版, 2020, 21(3): 70-77.
Chen Chushu, Sheng Chuan, Xie Junwei, et al. Research on the Deception of Direction-Finding System Based on FDA with Non-Linear Frequency Offset[J]. Journal of Air Force Engineering University: Natural Science Edition, 2020, 21(3): 70-77.(in Chinese)
[12] Ge J A, Xie J W, Wang B, et al. The DOA Location Deception Effect of Frequency Diverse Array on Interferometer[J]. IET Radar, Sonar & Navigation, 2021, 15(3): 294-309.
[13] 王昊飞. 基于OFDM信号的MIMO雷达反侦察性能分析[J]. 兵器装备工程学报, 2021, 42(9): 177-182.
Wang Haofei. Anti-Reconnaissance Performance Analysis of MIMO Radar Configured with OFDM Signal[J]. Journal of Ordnance Equipment Engineering, 2021, 42(9): 177-182.(in Chinese)
[14] 杨少委. 正交波形MIMO雷达射频隐身技术研究[D]. 成都: 电子科技大学, 2015.
Yang Shaowei. Research on Radio Frequency Stealth Technology for Orthogonal Waveform MIMO Radar[D]. Chengdu: University of Electronic Science and Technology of China, 2015. (in Chinese)
[15] 漆杨. MIMO雷达射频隐身性能研究[D]. 成都: 电子科技大学, 2012.
Qi Yang. Research on RF Stealth Performance of MIMO Radar[D].Chengdu: University of Electronic Science and Technology of China, 2012. (in Chinese)
[16] 葛佳昂, 谢军伟, 张浩为, 等. 频率分集阵列对干涉仪的角度欺骗效果[J]. 北京航空航天大学学报, 2019, 45(1): 183-191.
Ge Jiaang, Xie Junwei, Zhang Haowei, et al. Angle Deception Effect of Frequency Diversity Array on Interferometer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(1): 183-191.(in Chinese)
[17] Bergin J, Guerci J R. MIMO Radar: Theory and Application[M]. Boston: Artech House, 2018.
[18] 陳嘉贝, 王青平, 叶源, 等. 基于NSGA-Ⅱ的波前相位畸变特性分析[J]. 系统工程与电子技术, 2022, 44(5): 1439-1446.
Chen Jiabei, Wang Qingping, Ye Yuan, et al. Analysis on Wave-Front Phase Distortion Characteristics Based on NSGA-Ⅱ[J]. Systems Engineering and Electronics, 2022, 44(5): 1439-1446.(in Chinese)
[19] 王国伟, 王红卫, 张曦, 等. 交叉眼干扰的波前相位畸变特性研究[J]. 现代雷达, 2018, 40(10): 67-72.
Wang Guowei, Wang Hongwei, Zhang Xi, et al. A Study on Wave-Front Phase Distortion Characteristics of Cross-Eye Jamming[J]. Modern Radar, 2018, 40(10): 67-72.(in Chinese)
[20] 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2005.
Huang Peikang, Yin Hongcheng, Xu Xiaojian. Radar Target Characteristics[M]. Beijing: Publishing House of Electronics Industry, 2005.(in Chinese)
[21] ODonoughue N A. Emitter Detection and Geolocation for Microwave Warfare[M]. Boston: Artech House, 2019.
Analysis of Direction Finding Performance of Interferometer for
Frequency Division Orthogonal MIMO Radar
Abstract: The spatially synthesized signal pulse of the frequency division orthogonal MIMO radar has the characteristics of time-varying envelope and space-time coupling, which provides a new possibility for actively countering direction finding of the passive electronic reconnaissance system. This paper is dedicated to analyze the direction finding error of the electronic reconnaissance system to the frequency division orthogonal MIMO radar by the phase interferometer direction finding system. Firstly, the MIMO radar synthetic signal model is established for the far-field reconnaissance receiver, and then the influence of the time-varying envelope and phase wavefront distortion characteristics on direction finding performance are analyzed. Moreover, a feasible method based on initial phase modulation is proposed to increase the interferometers direction finding error. Simulation results indicate that the dominant regions of DOA estimation errors in interferometers are different due to the influence of phase wavefront distortion and instantaneous signal-to-noise ratio. In addition, the envelope fluctuation characteristics can be manipulated by phase modulation of MIMO radar elements, and the peak to average ratio (PAR) of the synthesized signal can be changed to increase the anti interception performance. In the analysis window of the interferometer, compared with the synthesized signal of phased array radar, when the prior position of the reconnaissance receiver is accurately known, the power of the MIMO radar synthesized signal can be reduced by 25 dB and it can also be reduced by 10 dB when the distance is unknown. Therefore, MIMO radar can increase the direction finding error of the interferometer to a certain degree.
Key words: MIMO radar; phase modulation; phase wavefront distortion; phase interferometer; direction finding error
