基于特征值分解和自适应滤波的极化相位优化方法

姜修成，张正加，王猛猛，刘修国，陈启浩

中国地质大学(武汉) 地理与信息工程学院,武汉 430078

1 引言

差分干涉测量DInSAR（Differential Interferometric Synthetic Aperture Radar）技术能够获取高精度、大范围的地表三维信息和变化信息，但是由于相位信息受大气效应和时间、空间去相干等偶然因素影响，使得该技术对缓慢形变的量测可靠性不高（廖明生和王腾，2014）。针对这一问题，研究学者们提出了永久散射体PSs（Persistent Scatterers）（Ferretti等，1999）和小基线集SBAS（Small Baseline Subset）（Berardino等，2002）等时间序列InSAR技术，可以有效减少时间和空间去相干的影响。但是，在一些低相干区域，早期的时序InSAR技术难以获取较多的稳定目标，难以准确地反映地表形变。针对这一现象，研究者们把关注点转移到了具有中等时序相干性的目标上，即分布式散射体DSs（Distributed Scatterers）。

2011年Ferretti 等（2011）提出了联合PS 目标和DS 目标的SqueeSAR 算法，可以有效增加相干点的数量，降低解缠的难度，且能够获取更完整的形变信息。但是相对于永久散射体，分布式散射体受时空失相干的影响更为显著，往往需要基于DS 目标同质像元散射特性的时序统计方法对相位进行优化处理，改善相位质量。因此，同质点的识别和 DS 的相位优化是 DS-InSAR 技术的2 个关键步骤。

在同质点识别方面，KS（Kolmogorov-Smirnov）、AD（Anderson-Darling）等非参数检验方法（Parizzi和Brcic，2011）已经广泛用于空间同质像元SHPs（Spatial Homogeneous Pixels）识别。基于SAR 影像单视复数据服从复圆高斯分布的假设，蒋弥等（2016）提出了快速同质点选取方法（FaSHPS），该方法无需逐个比较待估计像元与目标像元的函数分布，而是通过简单的逻辑判断确定目标像元的同质点，具有计算效率高，同质像元异质性小等优点。Narayan 等（2018）提出了相似时间序列干涉相位（STIP）像元来识别相似像元，改善了干涉像元的分类和相干估计。

在DS 目标相位优化方面，相位估计主要分为最大似然估计MLE（Maximum Likelihood Estimators）和近似特征值分解EVD（Eigenvalue Decomposition）估计两大类，Ferretti 等（2011）提出了该方向的先驱算法PTA（Phase Triangulation Algorithm）优化DS目标相位。Fornaro等（2015）提出了CAESAR算法，该算法通过主成分分析方法分解像元协方差矩阵，从而分离信号相位与噪声相位。Ansari等（2018）提出了基于特征分解的干涉相位最大似然估计器（EMI），该方法既保留了EVD 方法的计算高效性，又保持了PTA 算法的估计效率。Zhao 等（2019）提出了基于非线性优化估计（NLE）的DS相位估计算法，该算法在MLE 算法基础上添加了权重，最终能较好地降低DS 相位噪声，检测到更多的相干点。此外，Jiang 和Guarnieri（2020）采用参数bootstrap方法移除时空相干矩阵偏差，提高DSI技术的性能。

随着越来越多极化雷达卫星的发射，比如Radarsat-2，TerraSAR-X，ALOS-2 和Sentinel-1等，积累了大量的时序极化SAR 数据，为极化干涉研究工作提供了良好的条件。因此，Pipia 等（2009）提出了Pol-PSInSAR 技术，该技术结合不同极化通道来提高相干性，从而提高相干点的密度来改善对地表形变的监测和表征。然而，Pol-PSInSAR技术主要是针对PS目标。

由于现实场景中往往同时存在着DS 与PS 目标，Zhao和Mallorqui（2019c）提出了SMF-POLOPT算法，该算法采用MMSE 滤波方法处理DS 目标，然后利用振幅离差法和平均相干系数法自适应的优化PS与DS目标相位，提高了形变监测点的密度和降低了斑点噪声。由此可见，自适应极化优化算法联合处理PS与DS目标可以有效提高相干点目标密度和改善相位质量。

鉴于此，本文提出了一种可行的基于特征值分解和自适应滤波的极化相位优化方法（EVDFPO）。EVD-FPO方法基于Sentinel-1A双极化数据的幅度信息识别PS目标与DS目标，利用特征值分解极化相位优化技术和自适应滤波技术自适应的优化PS 目标与DS 目标相位。结果表明，EVDFPO 方法能够有效提高相干点密度和改善相位质量。

2 方法

2.1 极化SAR

本文主要利用Sentinel-1A VV、VH 极化数据的幅度信息，识别DS 目标和PS 目标。对于Sentinel-1 VV、VH 双极化数据，Pauli 散射矢量可以表示为（Shamshiri等，2018）

式中，SVV为同极化项，SVH为交叉极化项，T 代表矩阵转置。

则一个新的散射系数可以表示为（Zhao 和Mallorqui，2019b）

式中，μ为SAR 影像分辨率单元极化散射系数；w为酉矩阵投影矢量；H表示复共轭转置。

对于VV、VH 双极化数据，w可以表示为（Sadeghi等，2018）

式中，w为酉矩阵投影矢量；α和φ两个参数范围是已知的，α与目标的散射机制类型有关，φ与目标的散射方向有关。

2.2 DS目标与PS目标识别

2.2.1 PS目标识别

PS 目标在时间序列上具有强散射特性，因此可以根据SAR 影像的时间平均幅度值来识别PS 目标。Shamshiri 等（2018）表明，Sentinel-1A 双极化数据选取PS 目标的过程中，VV 极化与VH 极化都有一定的贡献。因此，本文同时考虑VV 极化和VH 极化数据的平均幅度信息，VV 极化数据的时间平均幅度设置阈值选取的PS 点表示为 PSs-VV，VH极化数据的时间平均幅度设置阈值选取的PS点表示为PSs-VH，最终PS目标为两种极化数据选出PS目标的总和。

2.2.2 DS目标识别

DS 目标在空间上具有连续分布的特性，因此可以通过判别一定空间范围内两样本时间维度的强度信息，来检验两样本的相似性。本文采用两样本AD（Anderson-Darling）检验方法初步识别DS 目标。由于空间上连续分布的水体等低相干目标幅度同样具有相似性，初步识别的DS 目标中往往包含水体、植被等低相干目标。而VV 极化幅度数据容易识别低相干目标，因此，本文利用VV 极化数据的时间平均幅度设置阈值剔除初始DS 目标中水体等低相干目标，得到最终的DS目标。

2.3 特征值分解和自适应滤波极化相位优化（EVD-FPO）

PS 目标信噪比较高，为了保护其分辨率，无需进行滤波降噪。而DS 目标像元的相位受时间和空间失相干的影响，存在着噪声相位，因此需要对新散射系数构成的SAR 影像中的DS 目标进行自适应均值滤波处理。自适应均值滤波如下（Zhao和Mallorqui，2019a）：

式中，ψc为中心像元相位；Nn为估计窗口内像元数总和；A(i)为第i个像元的振幅；ψ(i)为第i个像元的相位。

对于VV、VH 双极化数据得到的新散射系数构成的SAR 影像，同质点的后向散射信号并非完全一致，因此同质点的幅度并非完全相同，相较于协方差矩阵，相干矩阵能够有效避免振幅干扰，任一同质目标点的时间相干矩阵可以表示为（Navneet等，2018）

式中，y=[y1，y2，…，yn]T为μ=[μ1，μ2，…，μn]T归一化后的结果；μ2，…，μn]T表示同质点在N景SAR 影像上的复观测量；NSHPs为同质点数量；Ω表示同质点集合；H表示复观测量的共轭转置。

任一像元的后向散射都是子散射体散射信号的叠加，通过特征值分解可以分离出各子散射体的后向散射信号（Cao等，2016）。为半正定矩阵，根据特征值分解原理，可以表示为

式中，Λ为N×N维特征值对角矩阵；λi为特征值；σi为特征向量。

根据主成分分析原理，当特征值λi越大，其对应的子散射体占据像元整体散射信号的比重越大。将最大特征值对应的特征向量当作主散射体，其余特征值对应的特征向量当作噪声，相干矩阵表示为（Cao等，2016）

为了抑制新散射系数干涉相干信号中的噪声成分，可以通过最大化时间相干矩阵最大特征值的贡献率来提高主导散射体信号的比重，从而优化干涉相位。即

式中，λ1为第一主成分对应特征值；N为影像数量；α、φ两个参数范围是已知的，α与目标的散射机制类型有关，φ与目标的散射方向有关。

对于识别的PS 目标集，采用BGSM（Best Globle Scattering Mechanism）算法（Azadnejad等，2020）搜索全局最优投影矢量使得最大特征值（第一主成分）贡献率达到最大。对于DS 目标集，采用ESPO 方法逐像元搜索最优散射机制使得最大特征值贡献率达到最大。本文方法流程见图1 所示：（Ⅰ）为PS 目标识别与相位优化；（Ⅱ）为DS目标识别与相位优化。相位特征值分解极化相位优化示意图见图2，需要注意的是，特征值分解技术主要用于求解最优散射机制，并没有用于分解新散射系数的相位。

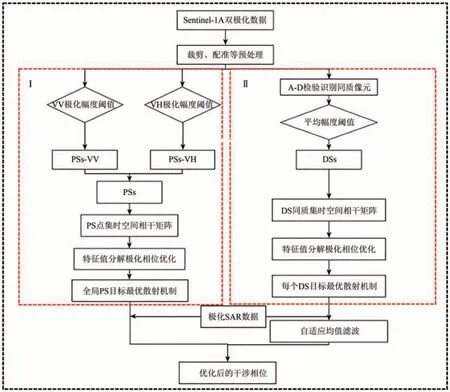
图1 EVD-FPO方法流程图（Ⅰ为PS目标识别与相位优化；Ⅱ为DS目标识别与相位优化）Fig.1 Flowchart of EVD-FPO（Ⅰ is the identification and phase optimization of PSs；Ⅱ is the identification and phase optimization of DSs）

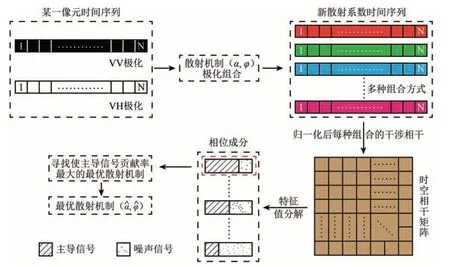
图2 特征值分解极化相位优化示意图Fig.2 Schematic diagram of eigenvalue decomposition polarization phase optimization

3 研究区与数据集

本文采用覆盖青藏铁路部分路段的Sentinel-1A VV、VH 双极化SAR 数据来完成提出的相干点目标识别与相位优化算法。该数据集包含17 景SAR 影像，时间范围为2017年3月21 日至2018年4月21日，重访周期为12 d，距离向与方位向视数比为4∶1，研究区大小为1000×1000像元，具体的影像参数信息如表1所示。本文的影像裁剪、配准预处理主要借助于SARscape 雷达影像处理软件（Sahraoui等，2006）。图3 为研究区遥感影像，主要包括青藏铁路、青藏公路、热融湖、高原荒漠、高原草甸和坡积物等地物类型。

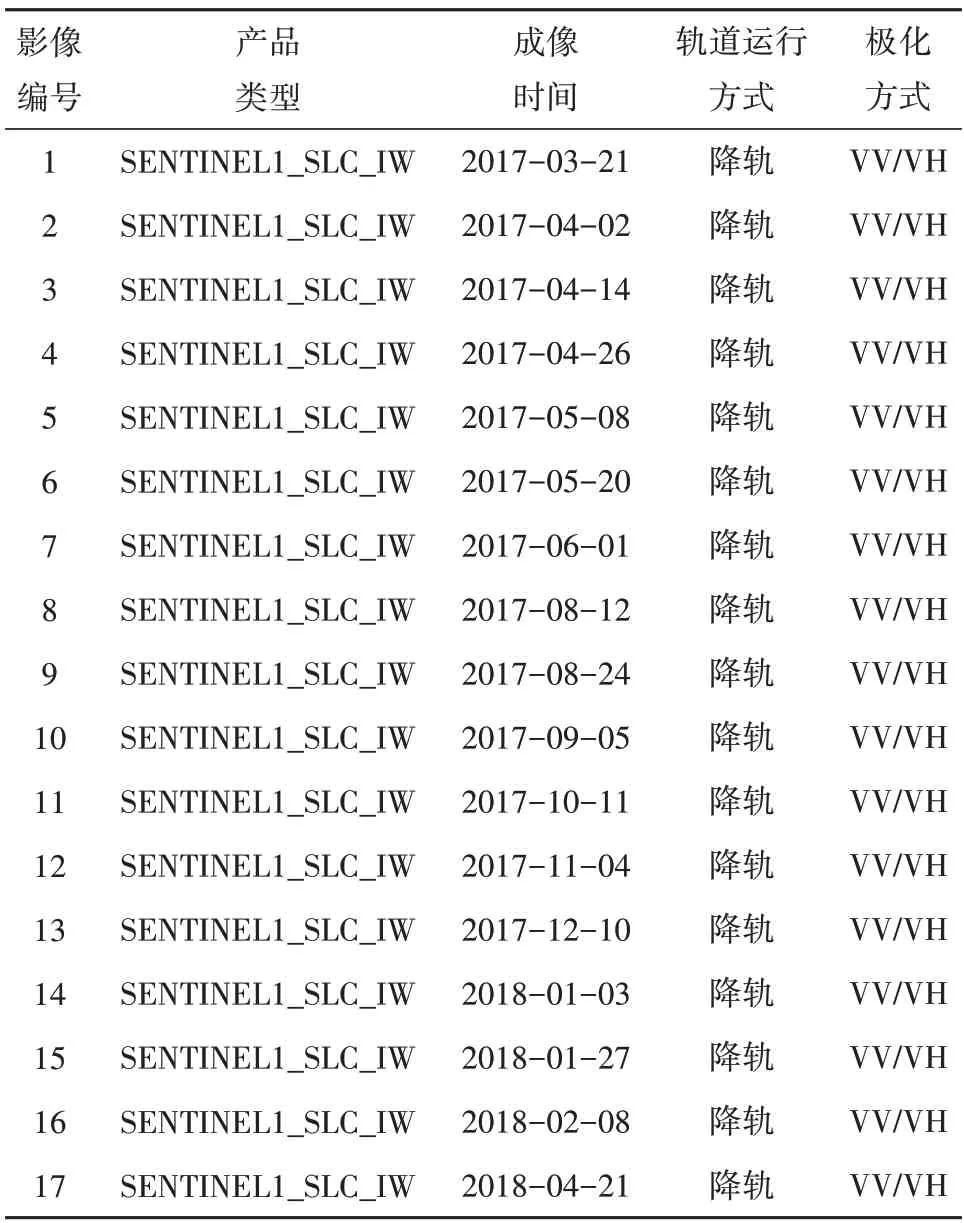
表1 Sentinel-1A SAR数据参数Table 1 Sentinel-1A SAR data parameters

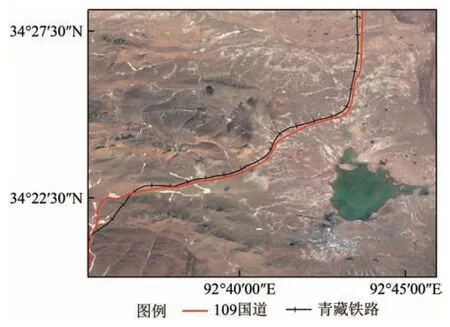
图3 研究区遥感影像Fig.3 Remote sensing image of study area

4 结果与分析

本部分主要从相干点目标密度与相位质量两个方面评估提出的方法，为了突出EVD-FPO 方法的优势，将与单极化DA法（VV-DA）、CAESAR 方法（Fornaro等，2015）以及ESM-DA方法（Navarro-Sanchez和Lopez-Sanchez，2012；Iglesias等，2014；Shamshiri等，2018）结果进行比较。其中EVD-FPO方法和ESM-DA方法需利用 VV、VH双极化数据优化相位，而DA法只采用VV极化，并没有优化相位。

4.1 相干点目标识别

EVD-FPO 方法中识别相干点目标分为PS 目标识别与DS 目标识别两个部分。PS 目标识别主要基于VV与VH 极化的平均幅度值以及研究区的特征，根据平均幅度值和青藏铁路、输电铁塔等强散射目标的散射特性对阈值进行调整，最终分别设置阈值0.55 与0.4 提取出强散射目标，如图4 所示。可见：VV 极化平均幅度图中提取的青藏铁路（虚线框线状地物）存在不连续的现象，而VH 极化平均幅度图提取的青藏铁路较为完整。VV 极化平均幅度图提取的输电线路铁塔（实线框内上下排列的点状地物）较VH 极化更为清晰。两种极化数据在提取强散射目标结果上存在着互补的关系，本文将2 种极化数据提取的结果合并，得到PS 目标点集，可以发现青藏铁路更加完整图4（a），输电线铁塔也更加明显。DS 目标识别主要分为以下两个步骤：第一步，采用A-D 检验识别同质像元，估计窗口大小为11×11，根据估计窗口的大小和研究区实际选取目标的效果设置DS 目标连通数量阈值为80，选取的DS候选点（DSC）结果如图5（a）所示，发现能够很好的排除青藏铁路等强散射目标，图5（b）为同质像元数量。由于水体呈空间连续分布，幅度具有相似性，高原湖泊和河流等低相干目标被误选为DS 目标。第二步，借助VV极化平均幅度图，在平均幅度阈值以下设置阈值并根据高原湖泊的散射特性进行调整，最终设置阈值为0.4，很好的剔除了水体等低相干目标，得到DS 目标如图5（c）所示。最终的DS 目标很好的剔除了低相干目标（高原湖泊）和PS 目标（青藏铁路，输电线路铁塔），与基于VV、VH 极化平均幅度选取的PS 目标结果互为印证。将PS 目标与DS目标整合到一起，最终EVD-FPO 法获取的相干点目标如图6（a）所示。对于单极化DA方法（VVDA）和ESM-DA方法，一般情况下，当像元振幅离差值小于0.25时，就判定该像元为PS目标候选点，由于本研究区相干点目标较为稀疏，故稍微增加振幅离差阈值大小来增加相干点密度，并通过设置双重阈值来剔除水体等低相干目标，故当振幅离差值小于0.35 且平均幅度值大于0.4时，将会被挑选为相干点目标，选取结果如图6（b）和（c）所示。本文的EVD-FPO 方法获取的相干点密度（数量为276362）是ESM-DA方法（数量为168164）的1.64 倍和VV-DA方法的9.06倍，相干点目标数量的改善主要是因为ESM-DA方法是通过提高PS目标的相位质量来增加相干点目标密度，而EVDFPO 则同时考虑了PS 目标和中等时序相干性的DS目标，高密度的相干点可以更好地探测和描述地表形变。

图4 VV极化、VH极化和极化叠加平均幅度图中的PS目标（红色虚线框内线状地物为青藏铁路，蓝色实线框内有序排列的点状地物为输电铁塔）Fig.4 PSs in the average amplitude image of VV，VH and polarization superposition（The linear features in the red dashed line frame are the Qinghai-Tibet Railway，and the dot-shaped features in the blue solid line frame are the transmission towers）

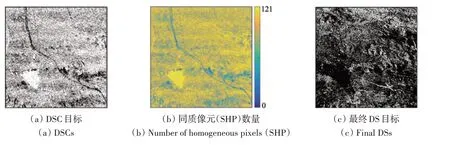
图5 DSC目标、同质像元（SHP）数量和最终DS目标Fig.5 DSCs，number of homogeneous pixels（SHP）and final DSs

图6 不同的目标识别方法选取的相干点Fig.6 Coherent points selected by different target identification methods

4.2 极化相位优化

极化干涉相位优化的过程是搜索最优投影矢量来提升相位质量。前文已经叙述，投影矢量w中的两个实参α和φ是与目标几何和电磁特性有关。α代表散射体内部的自由度，与目标的散射机制类型有关，取值范围0°— 90°（Cloude和Papathanassiou，1997）。对于只包含VV-VH双极化数据的Sentinel-1A来说，很难通过相干分解来提取精确的散射类型（Ji和Wu，2015）。α=0°可以是线性偶极子、表面散射或者二面角散射，而α=90°代表了随机体散射或者定向目标（Azadnejad等，2020）。α值越小，表明VV极化的贡献越高，反之，VH极化贡献越高。

为了调查研究区PS目标与DS目标的最优散射机制α和φ的特性，绘制了EVD-FPO 方法中PS 目标和DS 目标最优散射机制α和φ的分布直方图，如图7所示。

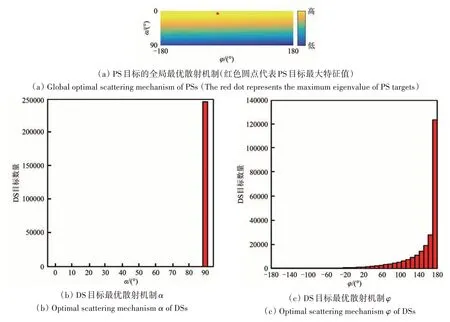
图7 EVD-FPO法优化PS目标与DS目标的最优散射机制统计直方图Fig.7 The optimal scattering mechanism histogram of PSs and DSs by the EVD-FPO method

由于研究区PS 目标主要为铁路、公路、输电铁塔和山体硬目标等地物，这类地物的散射类型由二面角散射主导，在α=5°，φ=-25°时取得了最大特征值贡献，表明了VV 通道在PS 目标相位优化过程中有更多的贡献，结果与文献（Azadnejad等，2020）较为吻合。

研究区的DS 目标主要来源于广泛分布的高原荒漠、高原草甸和坡积物等地物类型，这些地物的散射类型由随机体散射主导，在α=90°时DS目标取得最大特征值贡献，而φ值主要集中在180°，此时的相位贡献主要来源于VH通道。

为了检验EVD-FPO 方法求解PS 目标和DS 目标集的最优散射机制的可靠性，利用ESM-DA方法对本文方法选取的PS目标和DS目标进行优化得到最优散射机制作为参考和验证，结果如图8 所示。可见，ESM-DA方法优化PS 目标相位取得的最优散射机制α大部分在低值部分，而DS 目标相位优化取得的最优散射机制α大部分分布在高值部分，这表明了PS目标和DS目标的主要相位贡献分别来源于VV通道和VH通道。结果显示，ESM-DA方法与本文EVD-FPO 方法优化PS 目标与DS 目标相位得到的最优散射机制较为接近，验证了EVD-FPO方法求解最优散射机制的可靠性。

图8 ESM-DA法优化点目标的最优散射机制α直方图Fig.8 The optimal scattering mechanism α histogram obtained by optimizing targets by the ESM-DA method

VV 单极化数据采用DA法选取PS 目标，相位并没有优化。ESM-DA方法是逐像元计算振幅离差值，并搜索最优散射机制使得每个像元的振幅离差值最小，为了保护PS 目标分辨率，优化过程中无需对PS 目标进行滤波处理。CAESAR 方法联合中心像元及其窗口内同质像元估计平均协方差矩阵，并借助主成分分析的方法分离主导信号，达到了滤波和提取主导相位的效果。为了突出本文EVD-FPO方法对PS目标相位的保护，不对PS和DS目标进行任何滤波处理的特征值分解极化相位优化技术（EVD-PO）也用于与本文方法的比较。图9展示了干涉对20170426-20170508的干涉相位。其中：图9（Ⅱ）VV-DA方法PS目标相位；图9（Ⅲ）ESM-DA相干点目标相位优化结果；图9（Ⅳ）CAESAR方法相干点目标相位优化结果；图9（Ⅴ）EVD-PO 相干点目标相位优化结果；图9（Ⅵ）EVD-FPO 相干点目标相位优化结果。VV-DA方法选取的PS 目标过于稀疏，且并无滤波处理，相位中明显存在着斑点噪声。ESM-DA方法通过最小化振幅离差值来提升PS 目标密度和优化PS 目标相位，该方法主要适用于PS 目标较多的城市区域。在青藏高原地区，原本可能属于DS 目标的相干点经过极化优化后会被判定为PS 目标，这些相干点目标相较于真正的PS 目标包含许多噪声成分，但是ESM-DA方法很难区分真正的PS 目标和本属于DS 目标的PS 目标，在优化过程中无法通过滤波等处理降低相位噪声。CAESAR 算法基于VV 极化数据识别PS与DS目标，相干点的密度明显增加，且该方法在协方差矩阵估计过程中达到了滤波的效果，抑制相位噪声的效果比较明显，但是由于该方法只利用了VV 极化数据，难以提取完整的青藏铁路目标，导致了黑色虚线框内的青藏铁路相位出现了缺失。无滤波的EVD-PO 方法同时考虑了PS 目标与DS 目标，提高了相干点密度，相位连续性较ESM-DA更好，但是DS 目标中仍有许多斑点噪声。自适应均值滤波的EVD-FPO 方法在这些方法中表现最优，该方法同时优化PS与DS目标，既提高了相干点目标的密度，又采用自适应均值滤波降低了DS 目标的斑点噪声。此外，从图9（Ⅴ）和（Ⅵ）中黑色虚线框内的青藏铁路相位可以看出，PS 目标的相位在滤波前后并无变化，表明了本文EVD-FPO 方法将PS 目标与DS 目标分开处理，可以有效保护PS 目标的相位。对比图9（Ⅳ）和（Ⅵ）的红色虚线框内的DS 目标来看，CAESAR 方法DS 目标相位比EVD-FPO 方法DS 目标相位包含了更多的相位噪声。同样的，在图10所示的2017-04-26—2017-06-01 干涉相位中，可以得出相似的结论。

图9 干涉对为2017-04-26—2017-05-08的不同方法相位优化结果（Ⅰ为平均幅度图。Ⅱ—Ⅵ为Ⅰ图红色框区域放大，分别为VV-DA、ESM-DA、CAESAR、EVD-PO和EVD-FPO）Fig.9 The phase optimization results of different methods，and the interferometric pair is 20170426-20170508（Ⅰ is the average amplitude image.Ⅱ to Ⅵ are enlargements of the red box in Ⅰ.Ⅱ to Ⅵ are VV-DA，ESM-DA，CAESAR，EVD-PO and EVD-FPO，respectively）

图10 干涉对为2017-04-26—2017-06-01的不同方法相位优化结果（Ⅰ为平均幅度图。Ⅱ—Ⅵ为Ⅰ图红色框区域的放大，分别为VV-DA、ESM-DA、CAESAR、EVD-PO和EVD-FPO）Fig.10 The phase optimization results of different methods，and the interferometric pair is 20170426-20170601（Ⅰ is the average amplitude image.Ⅱ to Ⅵ are enlargements of the red box in Ⅰ.Ⅱ to Ⅵ are VV-DA，ESM-DA，CAESAR，EVD-PO and EVD-FPO，respectively）

在得到干涉图后，为了定量评价优化后的相位结果，本文采用相位导数变化指标来评估各相位优化方法的相位质量。相位导数变化的值如果是可以忽略的，那么相位数据就是好数据，也就是说平均相位导数变化的值越小，相位质量越高（王超等，2002）。

相位导数变化的定义如下：

取相位导数变化计算窗口大小为3×3，并分别计算所有像元的相位导数变化（全局相位导数）和相干点目标的平均相位导数变化（相干点相位导数），结果如下图11所示。就全局平均相位导数而言，ESM-DA方法的相位导数变化为1.22，CAESAR 方法的平均相位导数为0.998，EVD-FPO方法的平均相位导数变化为0.974。就相干点处的平均相位导数而言，ESM-DA方法的相位导数变化为1.184，CAESAR 方法的平均相位导数为0.854，EVD-FPO 方法的平均相位导数变化为0.810，表明了EVD-FPO 方法得到的干涉相位质量高于CAESAR方法和ESM-DA方法。

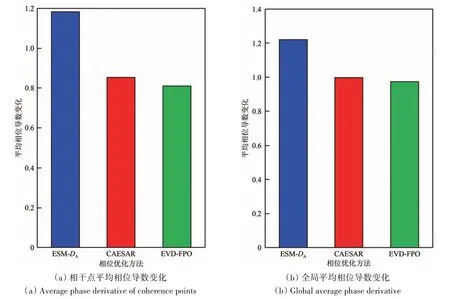
图11 不同相位优化方法的平均相位导数变化Fig.11 Average phase derivative of different phase optimization methods

5 结论

本文提出了一种时空间相干矩阵特征值分解和自适应滤波的极化相位优化方法（EVD-FPO），该方法主要基于BGSM，自适应均值滤波和特征值分解技术，能够将PS目标与DS目标分开处理。

为了评估提出的方法，将EVD-FPO 和 VVDA、CAESAR 以及ESM-DA方法进行比较。结果表明，EVD-FPO 方法选取的相干点目标密度得到了显著改善，相较于传统VV-DA和极化相干优化ESM-DA方法分别增加了9.06 倍和1.64倍，相较于单极化CAESAR 方法提取的青藏铁路目标更加完整。就极化优化的散射机制而言，EVD-FPO 方法与ESM-DA方法的最优散射机制较为接近，在研究区内（青藏高原沱沱河北部），PS目标相位的主要贡献来源于VV 极化，而DS 目标相位的主要贡献来源于VH 极化。就极化优化的相位结果而言，EVD-FPO 方法通过特征值分解和自适应均值滤波技术，将DS 目标与PS 目标分开处理，既降低了DS目标相位噪声，又保护了PS目标的相位，相较于CAESAR方法和ESM-DA方法有效改善了相位质量。