基于深度学习建表的宽域发动机火焰面燃烧模型构建与验证1)

于江飞 连城阅 汤 涛 唐 卓 汪洪波 孙明波

(国防科技大学空天科学学院高超声速技术实验室,长沙 410073)

引言

高超声速飞行器的飞行马赫数通常在4～6 之间,飞行高度在20 km 以上,具备超短时间内全球到达、快速远程打击的能力,具有相当高的民用和军用价值,而面向未来的新一代的宽速域高超声速飞行器设计飞行速度更快.超燃冲压发动机被认为是目前实现该类飞行器的最佳动力装置.随着计算机技术的长足发展,计算工具已经成为研发高效、高性能超燃冲压发动机的关键因素,可与试验手段结合加快研制进度.在现有的计算条件下,亟需适宜的模型和计算方式来精确有效地模拟超声速湍流燃烧,应用火焰面模型来模拟超声速湍流的燃烧过程是一种经济可行的办法.

火焰面模型是在Peters[1]对层流扩散火焰面的实验中给出的,其假设化学反应无限大,反应区域也无限薄的火焰面模型,而当无热辐射损失和扩散速率改变之后,火焰的热力学状态可以完全根据当地的混合状况确定,因此一般用混合分数来说明当地的综合状况.将层流火焰的火焰面模型拓展至湍流的燃烧中,则湍流的火焰可以被看作层流扩散火焰的集合.同时,标量耗散率可反映化学非平衡效应的影响.当气体均匀扩展时刻尺寸接近于化学反应时间尺寸时,将引起局部熄火;一旦随着传播时间尺度逐步缩小,就会发生整个湍流火焰的剥落甚至吹脱[2-5].进一步地,将火焰面模型推广至超声速流的合理性和可行性已经得到许多研究者的认可,并提出了多种可压缩性修正[6-14].其中,以Oevermann[6]提出的温度隐式求解方法最为经典,一度成为火焰面系列模型模拟超声速反应流的标准方法.

通常,层流火焰面库通过统计学方法实现与湍流流场的耦合,这样预先生成的湍流火焰面数据库在CFD 计算时被加载和查询.因此,火焰面模型的关键优势是即便涵盖了成百上千种组分的输运过程和详尽的动力学反应信息,也不需要苛刻的时间和空间分辨率以及大量的求解时长,只需要求解两个标量输运方程,就可以避免有限速率模型中存在的高度非线性动力学问题.因此,火焰面模型在从低速到超声速反应流中都有着广泛的应用,并且在考虑详细化学反应机理时有独到的优势,前景可谓广阔[15-18].

深度学习和神经网络是目前发展最快的研究和应用领域之一,吸引了众多学科的兴趣[19-21].陈尔达等[22]提出了一种基于残差神经网络的氢燃料超燃冲压发动机零维燃烧反应动力学计算方法,能够进行不同时刻温度、压力和组分浓度的快速预测.Guo 等[23]基于深度学习方法,搭建了一种融合壁面压力和纹影图像智能重构火焰发展过程的模型.这些方法有助于加速数值模拟的计算速度,为燃烧模型的智能化建立提供了新的研究思路.华为开发了盘古系列AI 大模型,其中包括NLP 大模型、CV 大模型和科学计算大模型,其中盘古气象大模型提出(3D earthspecific transformer,3DEST)来处理复杂的不均匀3D 气象数据,使用一个视觉Transformer 的3D 变种来处理复杂的不均匀的气象要素,并且使用层次化时域聚合策略,训练了4 个不同预报间隔的模型,实现了气象预报精度首次超过传统数值方法,速度提升1000 倍[24].

在回归分析中,人工神经网络模型(artificial neural networks,ANN)是学习过程中获取的用于存储和检索数据的计算模型.ANN 是一种很有前途的建模技术,具有很好的逼近能力.与制表方法相比,ANN 的主要优势在于其经济高效、平滑的函数替代和适度的内存要求,因为只需存储网络的结构、神经元突触的权重和偏差.将深度学习应用于超声速燃烧火焰面模型,为传统火焰面模型提供更加快速精准数值模拟的改进效果,在超燃冲压发动机燃烧室快速设计的工程领域存在非常具有潜力的应用价值.

2005 年,Flemming 等[25]对Sandia D 火焰进行了模拟,这是ANN 取代火焰面表格的第一次应用.神经网络的输入是混合分数及其方差和标量耗散率.输出是每种组分的质量分数(一个网络对应一种组分),并确认了表格的内存需求大约是神经网络需求的1300 倍.

Kempf 等[26]使用大涡模拟(LES)研究了扩散火焰的结构,采用一个由人工神经网络替代了的稳态火焰面模型来计算作为混合分数函数的流场参数,通过改变网格分辨率并与实验数据进行比较来评估结果的准确性,结果表明单点和两点统计结果与实验数据吻合良好.Ihme 等[27]使用两种化学表示方法即传统的结构化制表技术和ANN,对钝体稳定的甲烷/氢火焰进行了LES 模拟,用于生成最佳人工神经网络的方法(OANNs)[28]被用于这里的湍流反应流模拟.将该网络性能与提高了分辨率的结构化制表方法性能进行比较,并讨论了数值模拟过程中长期误差累积对统计结果的影响.

Owoyele 等[29]提出了一种分组多目标ANN 方法,将其应用于(engine combustion network,ECN)喷雾A 火焰条件下的正十二烷喷雾火焰特征,并通过LES 分析在不同环境条件下的全局火焰特征,以进一步检验其方式.然后,他们将相同的框架扩展到压燃式发动机中癸酸甲酯燃烧的模拟,给出了不同环境温度下的点火延迟时间和火焰抬举长度,并进行了基于ANN 的LES 计算和相同的框架进行四维线性插值,与实验结果进行了20 次比较.

Zhang 等[30]提出了ANN 技术与火焰生成流形(flamelet generated manifolds,FGM)相结合,以缓解FGM 模型的内存耗费大的问题,并通过数值模拟检验了ANN 预测精度.ANN 模型预测的物种质量分数与 FGM 表之间的误差称为预测损失.应用均方误差(MSE)损失函数来估计每个学习时期的预测损失.使用优化算法来减少模型的预测损失.他们所使用的优化算法是Adam,它通过随机梯度的下降程序来改变权重和偏差.为了对所有物种模型使用统一的学习率,在训练前将每个物种质量分数的范围缩放到0～1.然后在预测过程中重新缩小.学习 epoch的数量为 30000,这对于每个物种网络模型都是相同的.初始学习率设置为 0.001,并使用名为“ReduceLROnPlateau”的学习率调度器.ReduceLROn-Plateau 调度器允许当损失函数停止下降时动态降低学习速率.具体来说,一旦损失函数在100 个学习周期内停滞不前,学习率就会下降5 倍.首先,在混合分数-进程变量区间内,使用了68 个物质质量分数训练的ANN 模型;从喷雾燃烧的LES 和雷诺平均纳维-斯托克斯仿真(RANS)中能够检验出ANN 的预测准确性.结果表明,目前的 ANN 模型可以正确地复制FGM 表的大多数物种质量分数.在RANS和LES 中,采用相对误差小于5%的网络模型模拟发动机燃烧网络(ECN)喷雾H 火焰.首先在RANS框架下对该方法进行了验证.结果表明,该方法能较好地预测不同环境温度下喷雾和燃烧过程的变化趋势.结果表明,FGM-ANN 可以精确地模拟FGM 点火延迟时间(IDT)和火焰抬举长度(LOL),且与实验结果吻合较好.在ANN 的帮助下,FGM 模型可以实现高效率和高精度,并显著减少对内存的需求.

高正伟等[31]为了解决超临界小火焰燃烧模型数据库过于庞大,导致计算机内存不足和取值性能下降的问题,提出了使用ANN 进行建库的超临界小火焰/过程变量模型FPV-ANN,结果显示在准确性与传统FPV 方法一致的情况下,FPV-ANN 方法的计算速度比传统方法提升了30%.

基于深度学习改进的超声速燃烧模型[32-34],对于超声速湍流燃烧的数值模拟具有更高效的计算能力和较好的预测结果.通过深度学习改进的超声速湍流燃烧模型应用于超声速湍流燃烧计算,可以大大减轻气相计算的负载,必将为提高湍流数值模拟的计算效率和精度奠定基础.通过神经网络模型替代火焰面模型数据库,缓解内存占用压力,对之后的更高维度以及多组分火焰面模型应用于湍流燃烧模型仿真具有良好的潜在应用价值.

本文基于开源深度学习框架 PyTorch 建立神经网络模型,版本是Python3.6,Torch1.9 和Cuda11.1建立神经网络模型,训练模型使用的数据库由FlameMaster 软件生成,然后探究拓扑结构与神经网络不同函数对ANN 模型精度和效率的影响.最后选取飞行马赫数为4～12 的3 个发动机燃烧算例对改进后的模型进行测试和验证.

1 人工神经网络模型构建

在回归分析中,人工神经网络模型是在学习过程中获得用以存储检索数据的计算模型.在ANN 框架中,每个组分的质量分数以及进度变量源项QC和释热率HRR 不是从FPV 表中插值,而是从一个预先训练的ANN 模型中计算得到.

1.1 数据库划分

以氢气/空气燃烧为例,通过FlameMaster 得到的数据库作为样本集,数据信息包括混合分数Z,进度变量C,混合分数方差Z'',9 组分质量分数即: O2,H2O,H2,O H,O,H,H2O2,H O2和 N2,进度变量源项QC和释热率HRR.其中9 组分质量分数在每一组数据中总和为1.数据库中混合分数的范围是[0,1],均匀离散了201 个点;混合分数方差的范围是[0,Z(1-Z)],均匀离散了100 个点;进度变量的范围是[0,1],均匀离散了51 个点.这样数据库大小为201×100×51.

数据库以txt 格式保存,PyTorch 最基本的操作对象是张量,读取数据库时需要将数据库转为张量形式.每个数据集既是训练集也是测试集,当训练需要时,将训练集和测试集分类好后,可以使用不断迭代的随机种子,进行反复地重新训练建模,并从不同的模型上选取超参数.

1.2 数据归一化

火焰面/进度变量模型数据库的几种组分以及进度变量源项和释热率往往存在较大的数量级差别,神经网络预测结果会有较大的误差,因此使用神经网络分析时需要先进行归一化.归一化处理的目的是提升数据的内聚性,降低离散性,进而清除数据尺度差异对ANN 模型学习能力和预测精度的影响,提高模型的训练效率.本文采用最小最大值归一化

把原始数据变换到0～1 范围内,可以求得经归一化后的计算结果,当中Xmax为样本数据的最大值,Xmin为样本数据的最小值.归一化处理方法对不同量级数据都进行了无量纲化,并统一测量指标,能够防止净输入绝对值太高而造成的神经元数据饱和问题.与此同时,归一化使得开展梯度下降优化时学习率不再需要根据数据范围做调整,使用统一的初始学习率对于Adam 更新学习率效率更高,使模型更容易收敛.

1.3 人工神经网络模型训练

目前,人工神经网络的研究主要使用由Rumelhart等[35]给出的误差反向传播算法(back propagation,BP).BP 神经网络是一个使用误差逆向传递方法进行研究的多层前馈神经网络,是目前使用得最为普遍的神经网络.在BP 网络的输入层与输出层之间有一些神经元,这种神经元叫做隐藏层,它和外界并没有直接的关系,只是由权重和偏置常数的改变来控制输入层和产出的相互作用,每一神经元中间可能包含着若干个节点.网络的一个关于神经元计算原理的基本公式是神经元变量N是n-th 层神经元的个数,矩阵和向量是要训练的n-th 层的权值和偏值,f是激活函数.前一层神经元通过权重和偏置常数的线性组合结果,经过非线性激活函数f得到神经元 ϕn+1的输出.

ReLu 激活函数的收敛速率很高,而且在正值范围内(x>0) 就可以对抗梯度消失现象.分别引入MSE 损失函数和Huber 损失函数,公式分别如下

MSE 损失函数

Huber 损失函数

Huber 损失是平方数损失与绝对值损失的结合,它同时解决了平方数损失与绝对值损失的缺陷,不但使损失函数有了连续性的导数,而且同时运用MSE 梯度随参数递减的优点,也可以得到比较准确的最低位.不过由于Huber 损失函数中引入了额外的系数,因此训练量也必然增大,所以对于最终模型的练习效果和准确性都未必比MSE 好,后面会进行进一步分析探讨.选择的优化器为Adam 并使用学习率调制器,Adam 优化器的优点在于有效控制学习率步长和梯度方向,防止梯度的振荡和在鞍点的相对静止.但是后期Adam 学习率太低,影响有效收敛,因此使用学习率调制器解决Adam 后期因为学习率不变导致难以收敛的问题.

1.4 训练结果分析与评价指标

得到训练完成的模型后,通过原有的数据集对模型进行读取并比较预测值与真实值的差距.本文以平均相对误差MRE和皮尔森(Pearson)积矩相关系数(PPMCC)R以及线框图来评价ANN 模型的性能.平均相对误差MRE越小,皮尔森系数R的值越趋近于1,线框图中预测值曲面和真实值曲面重合越多,表明模型的预测效果越好.

平均相对误差

Pearson 积矩相关系数R

其中YANN代表预测值,YFPV代表真实值,是YANN的平均值,是YFPV的平均值,Ns代表样本数量.

2 不同函数结构对模型的影响

2.1 模型拓扑结构影响

人工神经网络模型的输入层由3 个神经元组成,分别是进度变量C、混合分数Z以及混合分数方差Z",即 ϕi=3 .输出层由11 个神经元组成,分别是9 组分质量分数即 O2,H2O,H2,O H,O,H,H2O2,HO2和N2,进度变量源项QC和释热率HRR,即ϕ0=11 .隐藏层层数为5,其中第2 层神经元数量为第一层神经元数量的2 倍,即N2=2N1,第3 层神经元数量为第2 层的2 倍,即N3=2N2,第四层神经元数量等于第2 层,即N4=N2,第5 层神经元数量等于第1 层,即N5=N1.采用试错法探究神经元个数Ns对ANN 模型的预测效果的影响.接下来将统一使用MSE 损失函数和Adam 优化器以及学习率调制器训练模型,只选择不同的神经元数量,得到不同的神经网络模型,并将数据库加载到这些模型中得到结果并分析.图1 和图2 是选择不同数量的第1 层神经元数量N1得到的模型导出后输出的预测值与真实值的皮尔森系数R和平均相对误差MRE.

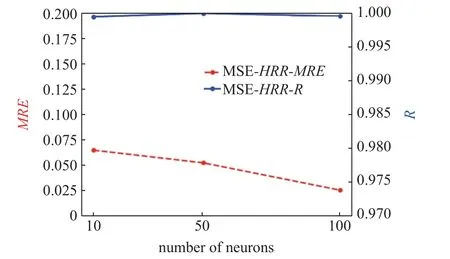
图1 神经元节点数对释热率HRR 模型精度的影响Fig.1 The effect of the number of neuron nodes on the precision of the heat release rate HRR model

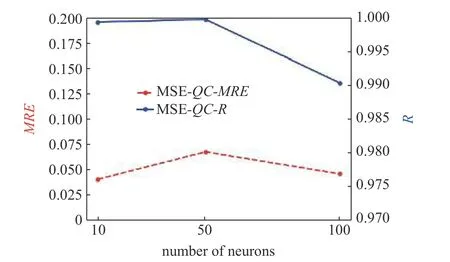
图2 神经元节点数对进度变量源QC 模型精度的影响Fig.2 The effect of the number of neuron nodes on the precision of the source term QC model for progress variable equation

由图1 和图2 可知,当隐藏层第1 层神经元个数为50 时,皮尔森系数R最接近于1,也就是线性相关性最高.对于HRR来说,第1 层神经元数量从10 到50 再到100,平均相对误差MRE是依次降低的,表明对于释热率来说,神经元数量越多模型预测性能越好.但是对于QC来说,神经元数量为50 时,平均相对误差反而最大,说明神经元数量对于不同参数的模型影响效果不同.

总的来说,模型的线性回归性都比较符合预期,此时更应该关注模型所占空间大小与训练效率.根据各个不同神经元数量模型的文件大小,N1=10时HRR模型大小为33.1 kB,N1=50 时HRR模型大小为222 kB,N1=100 时HRR模型大小为811 kB.N1=10 时QC模型大小为32.8 kB,N1=50 时QC模型大小为229 kB,N1=100 时QC模型大小为831 kB.

更加直观的线框图可以表现数据集经过人工神经网络模型输出的预测值与数据库的真实值的拟合效果如图3.随着神经元数量的增加,人工神经网络模型的文件大小也是不断增大的.因此在后续的优化模型中,选择第一层神经元数量为10 为最佳神经元数量,不仅有利于降低运行时内存的消耗,也有利于后续程序的耦合.

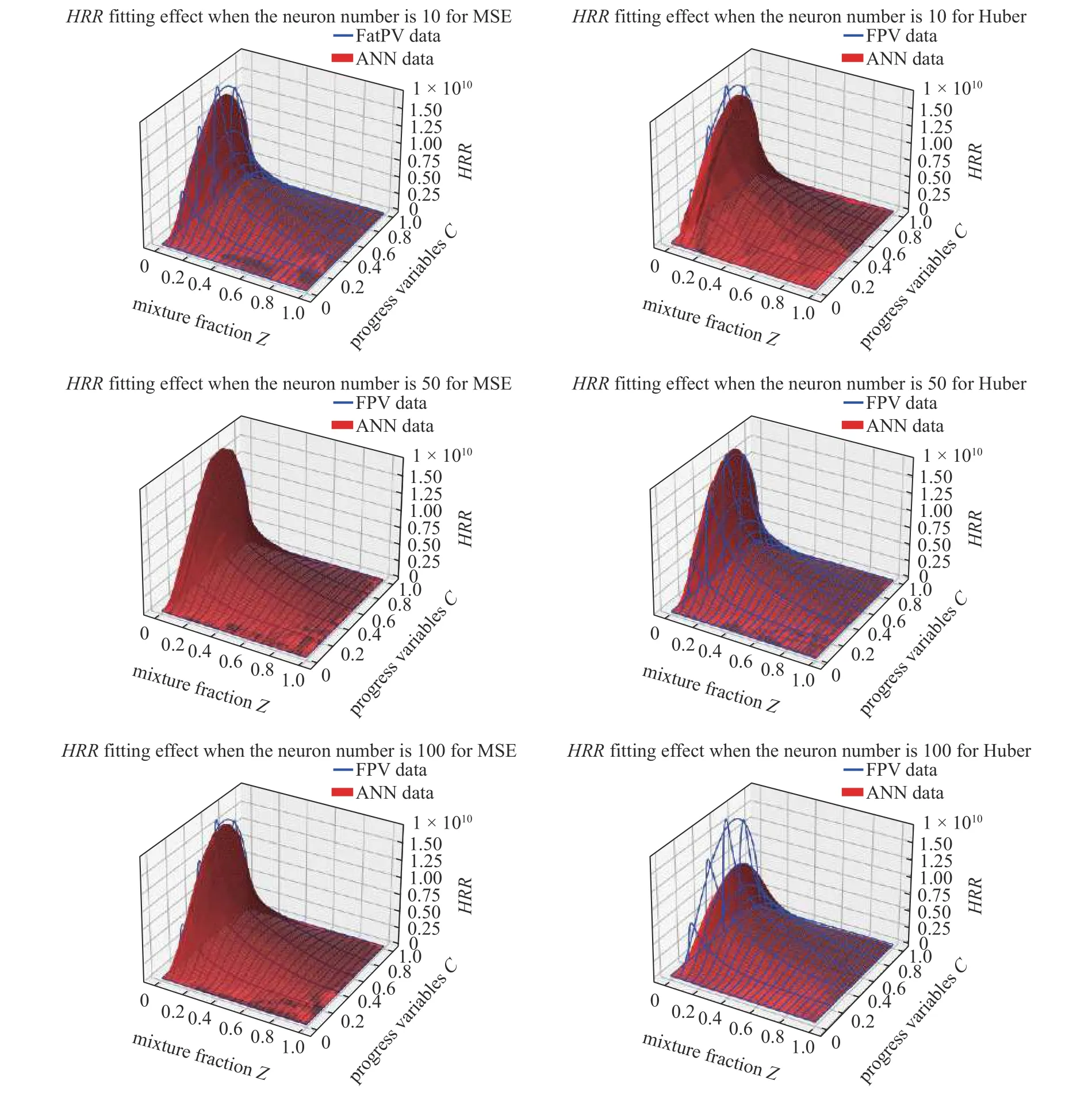
图3 神经元节点数对模型拟合效果的影响Fig.3 The effect of the number of neuron nodes on model fitting performance

2.2 损失函数不同选择的影响

在目前最主要的神经网络建模练习流程中,通常采用MSE 损失函数,有的文献也采用Huber 损失函数,下面探讨利用这2 个函数对模型的训练效果与准确度有何影响.

首先是讨论MSE 损失函数和Huber 损失函数的差异性以及各自的优缺点.MSE 函数的曲线比较平滑,便于采用梯度下降算法,计算成本也较小,而且收敛速率比较快.但是平方误差也有其缺点,当真实值和预测值差异过大时,经过MSE 损失函数会导致误差增大,如果碰到离群点可能导致梯度爆炸问题,从而影响模型的整体性能.Huber 损失函数同时解决了平方损失与绝对损失的缺点,使损失函数弱化了对离群点的过度敏感问题.在实际应用中,由于还有神经元数量、优化器选择等不同因素的影响,还需要对MSE 损失函数和Huber 损失函数的预测精度进行比较.

在图4 中可以发现,Huber 损失函数的MRE比MSE 损失函数大一个数量级,虽然在神经元数量为50 时,QC和HRR表现优异,但是总体的R值都不如MSE 损失函数.

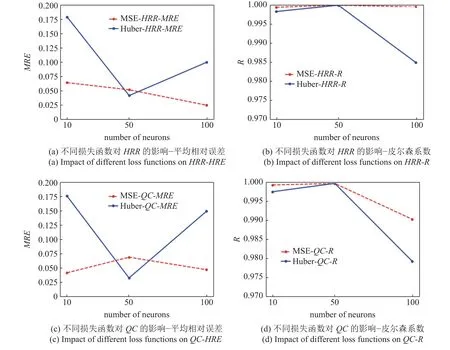
图4 不同损失函数对模型精度的影响Fig.4 The effect of different loss functions on the model accuracy

在图5 中可以发现在神经元数量为100 时,Huber损失函数对于数据释热率和进度变量源项的拟合都出现了明显的过拟合问题,而MSE 损失函数较好地拟合了数据库.同时Huber 损失函数进行模型训练时收敛速度也远远慢于MSE 损失函数,对此可以认为,在火焰面/进度变量模型训练中,MSE 损失函数是比Huber 损失函数更优的选择,在后续的CFD 计算中神经网络模型采用MSE 损失函数训练得到.

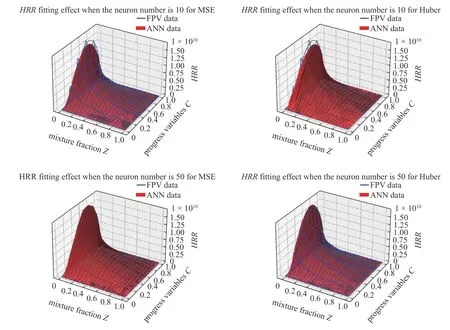
图5 损失函数对模型拟合效果的影响Fig.5 The effect of loss function on model fitting performance

2.3 学习率调制器的影响

Adam 和SGDM 是目前人工神经网络模型训练最常用的两个优化器.它们分别在效率和精度方面有着各自的优势.而优化器配合学习率调制器,训练过程中损失函数值达到设定的阈值后通过调制器不断降低学习率则有助于模型训练收敛.接下来针对使用Adam 优化器的人工神经网络模型,设定第1 层神经元数量N1,验证有无学习率调制器对HRR模型训练的影响.

图6 显示了有无学习率调制器对模型精度的影响.可以发现增加学习率调制器后,不论是平均相对误差更接近于0 还是皮尔森系数更接近于1 都有明显的效果.并且在训练过程中可以发现,没有学习率调制器的情况下由于学习率一直保持不变,损失值一直上下起伏变化,得到的相关误差无法稳定下降,训练时长比有学习率调制器慢好几倍,因此学习率调制器的加入是必要的.

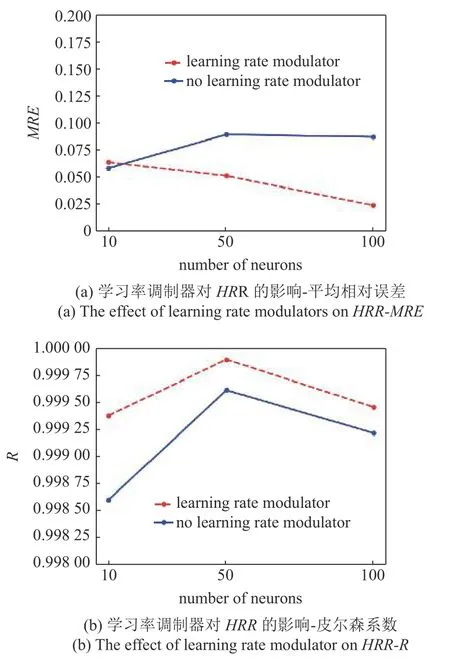
图6 学习率调制器对模型精度的影响Fig.6 The effect of learning rate modulators on model accuracy

2.4 主要参数的线性回归率

图7 给出了FPV 表和ANN-FPV 模型预测的O2,HRR和QC的回归图以及皮尔森系数R值.O2的R系数最大,HRR最小,QC介于两者之间.直线y=x是回归线,点落在这条线上表明ANN-FPV预测的组分质量分数与FPV 的基本一致.

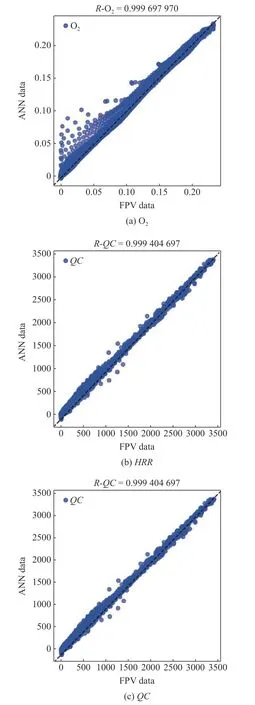
图7 O2,HRR 和QC 的回归图Fig.7 Regression plot of O2,HRR,and QC

3 内存占用优化的讨论

在通常的基于CPU 的CFD 求解器中,一个双精度标量占有64 位,即7.63×10-6MB.为了获得高分辨率的FPV 表,在FlameMaster 中将Z的网格数设置为10251,C的网格数设置为51,Z''网格数设置为100,并且在Z的上半部分和Zst附近对网格进行细化.FPV 数据库共有10 组数据,包括8 种组分质量分数、释热率HRR以及进度变量源项QC.正常采用CPU 计算火焰面模型占用的内存容量为:10×10251×51×100×7.63×10-6=3988.97 MB.在一个典型的64 核计算机集群中,内存成本将会是原本的64 倍,即255294.18 MB,这几乎是任何超级计算机都负担不起的.这是因为CPU 求解器在计算时采用了分解域的方法,每个分解出来的域都需要加载一次整个FPV 表.因此,本文将人工神经网络模型与FPV 结合并运行在GPU 上来减少内存占用,从而使得这种具有发展前景的湍流燃烧模型更加具有经济性.

CPU 由算术逻辑单元(arithmetic and logic unit,ALU)和控制器(control unit,CU)以及若干个寄存器和高速缓冲存储器组成,主要进行逻辑串行运算.而GPU 拥有大量ALU 用于数据处理,适合对密集数据进行并行计算,因此GPU 被大量用于AI 训练等并行计算场景.在英伟达显卡中有CUDA 核心,CUDA 中线程可以分为3 个层次:线程、线程块和线程网络.线程是基本执行单元,每个线程执行相同代码.线程块(block)则是若干线程的分组,可以是一维、二维或三维.线程网络(grid)是若干线程块的网格.GPU 上存在很多计算核心(streaming multiprocessor,SM),在具体计算时,一个SM 会同时执行一组线程,这一组数量一般为32 或64 个线程.一个block 绑定在一个SM,若这个block 中存在1024 个线程,这个SM 可以同时执行64 个线程,那么就会分成16 次执行.GPU 和CPU 也一样有着多级缓存还有寄存器的架构,把全局内存的数据加载到共享内存上再去处理可以有效地加速.

在使用GPU 计算火焰面模型时,可以自行设定batch size,也就是一次训练抓取的数据样本数量.batch size 的大小决定了计算速度,但是不会出现如CPU 计算时遇到的占用内存过大便无法运行的情况,可以对FPV 进行分批次处理,将数据加载到GPU 专用内存中.GPU 计算的另一个优点就是同时计算所有设定的数据集,而CPU 只能对多个域进行分步计算,GPU 的并行计算速度比CPU 快好几个数量级.

4 宽域发动机改进模型算例测试

宽域发动机中的燃烧流场包含复杂的激波膨胀波系,不同压力下化学反应速率明显不同,传统的火焰面/进度变量(FPV)模型仅使用一个基于燃烧室平均压力建立的火焰面数据库,因而不足以描述压力剧烈脉动的燃烧流场.发动机内的燃烧近似为等压燃烧,压力为当地环境压力,因此火焰面数据库的建库压力应与当地环境压力一致,以提高模型精准度.然而,对流场中所有压力生成火焰面数据库将会占用非常大的内存空间,直接将压力作为火焰面数据库的维度可能带来巨大的内存负载.本项目使用神经网络训练这个包含多个不同建库压力的火焰面数据库集合,相当于在混合分数、混合分数方差和进度变量维度之外,额外增加了压力的维度,并且训练后的神经网络模型(ANN-FPV)可以替代庞大的数据集以减轻内存压力,同时大大改进燃烧流场预测精度.

添加了压力维度的ANN-FPV 模型训练好后,为了测试其对FPV 数据库替代的效果,需要进一步以定量的方式分析,以下面3 个发动机算例为具体研究对象,通过耦合FPV 模型的RANS 方法,对ANN-FPV 替代FPV 数据库后的火焰面/进度变量模型开展验证与分析.

4.1 算例1:日本JAXA 机构Ma12-02 发动机

本算例为日本宇航研究开发机构JAXA 开发的M12 系列发动机[36-37],并在位于日本宇宙航空研究开发机构Kakuda 太空推进中心的高焓激波风洞(HIEST)中进行了试验.图8 所示为M12-02 发动机的示意图.流道的总长度为2889 mm.入口处的高度和宽度分别为250 和200 mm.燃烧室是一个宽度为70.7 mm、长度为1700 mm 的等直管道.超混合喷嘴(hyper-mixer injector)安装在入口后的上下壁面上,如图9 所示.喷嘴的前缘带有一个压缩斜坡,位于入口出口下游100 mm 处.从喷嘴上侧延伸的6 个宽度为20 mm 的压缩斜坡交替布置在上下壁面上.模拟飞行马赫数12 的实验工况如表1,其中给出的温度和压力分别为静温和静压.

表1 M12-02 实验超声速来流和燃料射流工况Table 1 Supersonic inflow and fuel jet conditions for M12-02 experiment

图8 M12-02 燃烧室构型 (单位:mm)Fig.8 M12-02 combustion chamber configuration (unit:mm)

图9 超混合喷嘴尺寸 (单位:mm)Fig.9 Hyper-mixer injector size (unit:mm)

计算采用结构/非结构混合网格,大小为1500 万,计算域为整个构型的1/4.计算区域包含发动机部分进气道,来流马赫数为6.72,静温为677 K.图10 显示了本算例传统模型(图10(a))与智能化改进模型(图10(b))计算温度分布云图,图11 对比了壁面压力沿程分布计算与实验结果,并给出了相对平均计算误差值.以压力参数P为例,这里的平均误差公式为,其中exp 代表实验数据,num 代表计算数据,n代表实验数据点数.本文所有算例的误差计算均采用该公式.表2 显示了算例1 的误差减小情况,平均误差减小了53.2%.

表2 算例1 误差减小情况表(飞行Ma12、计算入口Ma6.72、平均误差减小53.2%)Table 2 Error reduction in case 1 for intelligent improved combustion model (ANN-FPV) compared with tranditional model (FPV)(with flight Ma12,inlet Ma6.72 and average error reduction 53.2%)

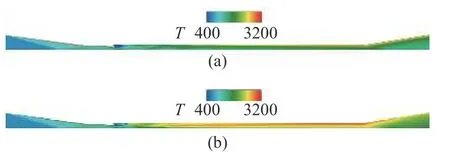
图10 算例1 流向中心截面上(a)传统模型与(b)智能化改进模型计算温度云图Fig.10 Case 1:Temperature contour in the flow direction center section calculated using (a) traditional model and (b) intelligent improved model

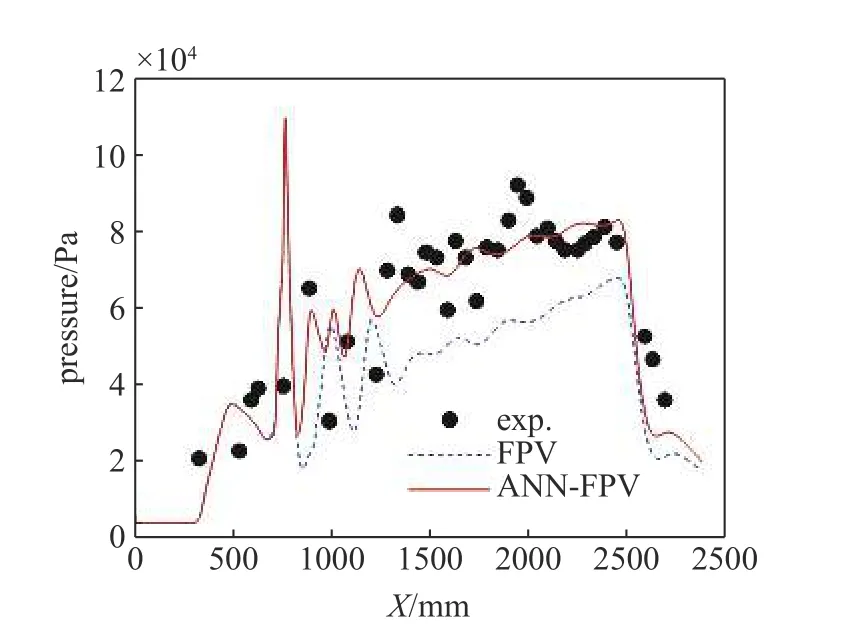
图11 算例1 壁面压力沿程分布计算与实验结果对比图(平均误差减小53.2%)Fig.11 Comparison between calculated and experimental results of wall pressure distribution along the flow path for case 1 (average error reduction is 53.2%)

4.2 算例2:美国伊利诺伊大学圆管燃烧室

该算例对象是伊利诺伊大学ACT-II 乙烯燃料的轴对称超燃冲压发动机[38],如图12 所示.轴对称隔离段长256 mm,下游轴对称凹腔深11 mm,长35 mm,后缘角22.5°.来流总温2196 K,总压160 kPa,模拟飞行马赫数约为8.乙烯燃料从凹腔上游42 mm 的16 个周向均匀分布的喷孔以45°喷注,具体的喷注和来流条件如表3 所示.

表3 算例2 圆管燃烧室工况Table 3 Operating conditions of the circular tube combustor of case 2

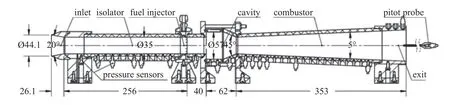
图12 算例2 圆管燃烧室的总体构造和具体尺寸 (单位:mm)Fig.12 Case 2:Overall structure and specific dimensions of the circular tube combustor (unit:mm)

计算采用结构网格,大小为1100 万,计算域为全尺寸的1/4.图13 显示了本算例传统模型(图13(a))与智能化改进模型(图13(b)) 计算温度分布云图,图14 对比了壁面压力沿程分布计算与实验结果.表4显示了算例2 的误差减小情况,平均误差减小了55.7%.

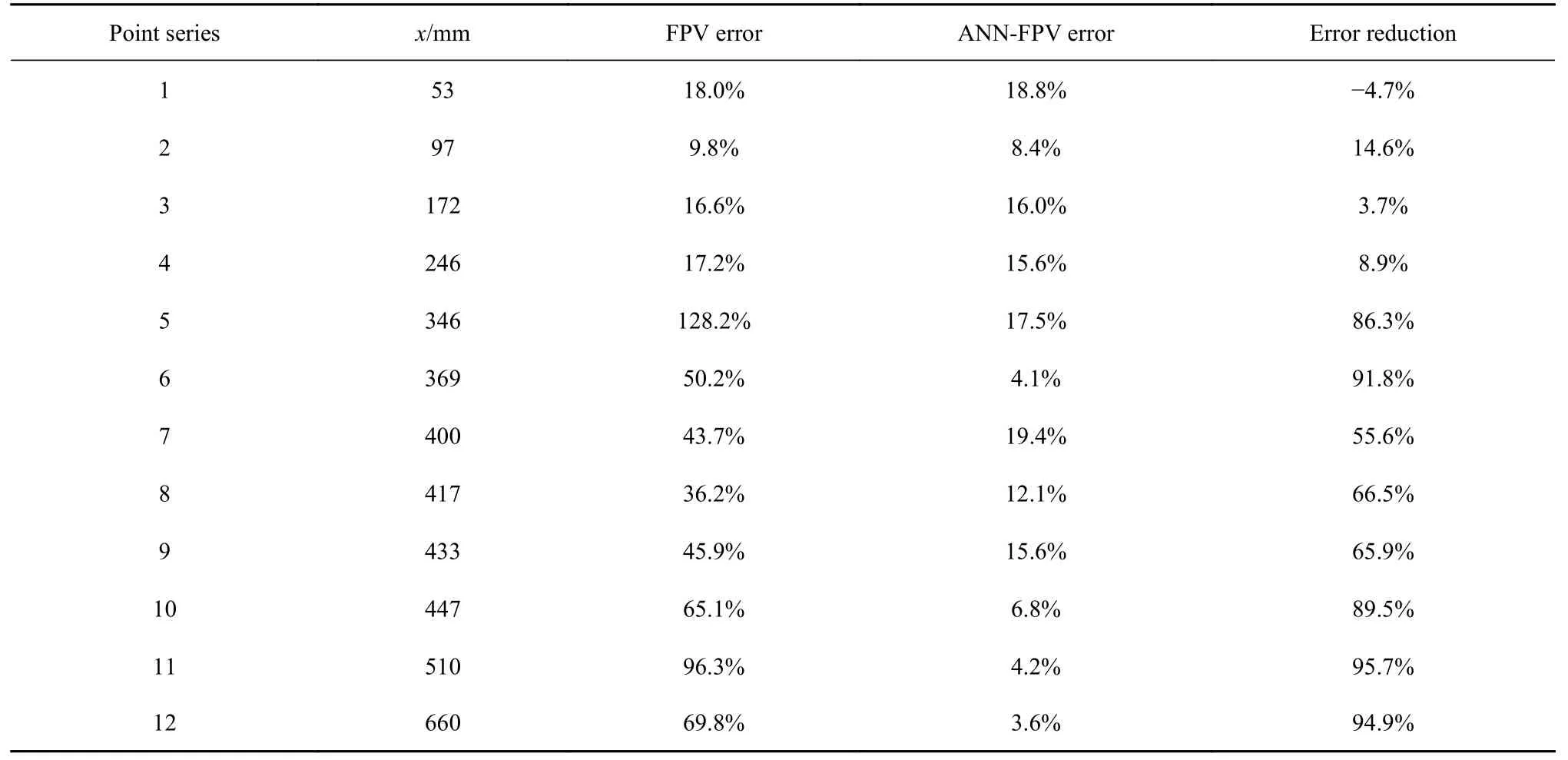
表4 算例2 误差减小情况表(飞行Ma8、计算入口Ma4.5、平均误差减小55.7%)Table 4 Error reduction in case 2 for intelligent improved combustion model (ANN-FPV) compared with tranditional model (FPV)(with flight Ma8.0,inlet Ma4.5 and average error reduction 55.7%)

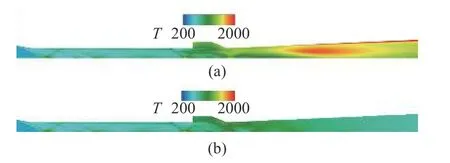
图13 算例2 流向中心截面(a)传统模型与(b)智能化改进模型计算温度云图Fig.13 Temperature contour in the flow direction center section calculated using (a) traditional model and (b) intelligent improved model of case 2

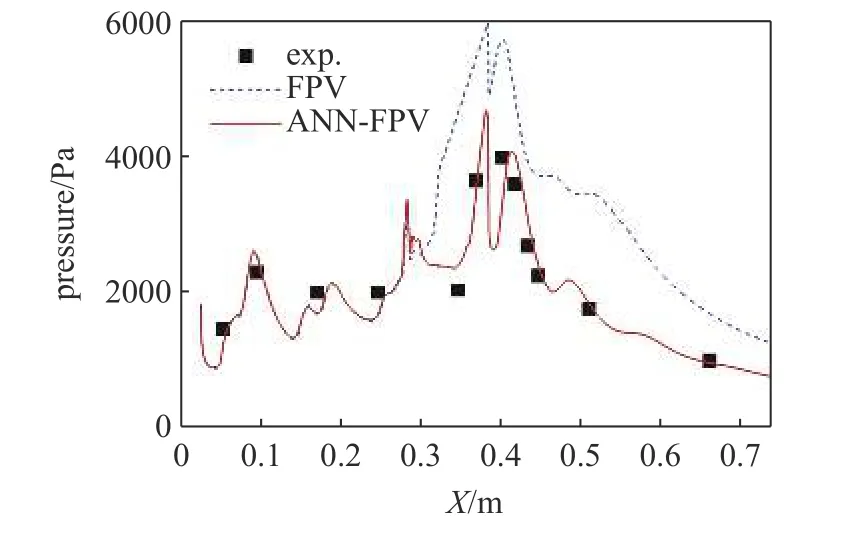
图14 算例2 壁面压力沿程分布计算与实验结果对比图(平均误差减小55.7%)Fig.14 Comparison between calculated and experimental results of wall pressure distribution along the flow path for case 2 (average error reduction is 55.7%)

4.3 算例3:中国空气动力研究与发展中心氢气凹腔燃烧室

本算例是基于中国空气动力研究与发展中心的氢气凹腔燃烧室实验[39].发动机全长约1073 mm,隔离段总长300 mm;模型隔离段入口为矩形截面,尺寸30 mm×150 mm,火花塞位于台阶下游75 mm 处,氢气喷注位置位于台阶上游10 mm 处,喷注孔φ1.0×15,孔之间间距为6.814 mm,最外侧的两个孔距侧壁27.3 mm;凹腔深度为11 mm,长度为121 mm,后斜坡角为21.1°.扩张段分4 部分扩张,具体见图15.

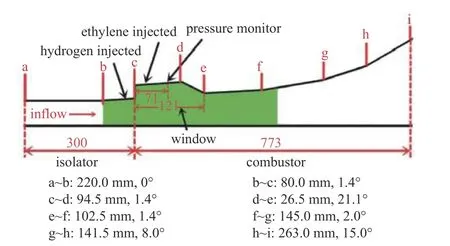
图15 算例3 氢气凹腔燃烧室构型示意图 (单位:mm)Fig.15 Schematic diagram of the configuration of the hydrogen-fueled cavity combustion chamber of case 3 (unit:mm)

实验模拟飞行马赫数4.0 的来流条件,如表5 所示,对应隔离段入口马赫数Ma=2.0,总温Tt=950 K,总压Pt=0.82 MPa.来流组分O2,H2O 和N2的摩尔分数分别为21%,12%和67%.燃料喷注条件为:先锋氢喷注压力4.0 MPa,对应当量比约为0.33.

表5 算例3 氢气凹腔燃烧室算例工况Table 5 Operating conditions of the hydrogen-fueled cavity combustion chamber of case 3

计算采用结构网格,大小约840 万.图16 给出了本算例传统模型(图16(a)) 与智能化改进模型(图16(b))计算温度分布云图,图17 对比了壁面压力沿程分布计算与实验结果.

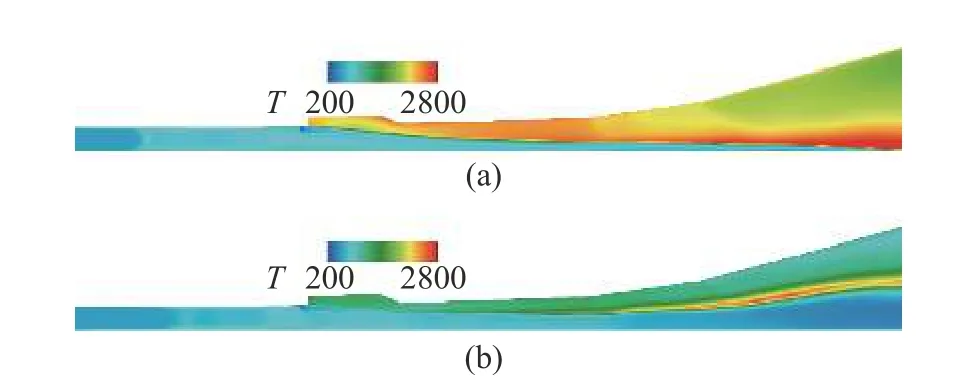
图16 算例3 流向中心截面(a)传统模型与(b)智能化改进模型计算温度云图Fig.16 Temperature contour in the flow direction center section calculated using (a) traditional model and (b) intelligent improved model of case 3

分别采用模拟飞行马赫数为4,8 和12 的3 个燃烧算例对改进模型进行了验证,通过与已知的文献实验结果做出比较得到计算误差,表6 显示了燃烧模型验证算例误差减小情况.结果表明智能化改进的模型比传统的模型平均误差减小量均超过了50%,算例误差最大减小值可达57.2%.

表7 显示了3 个算例分别采用两种燃烧模型的CFD 结果,包括了时间消耗值及比值、内存占用及比值和精度提升值,可以看到改进模型的耗时比传统模型高了70%左右,未来需要进一步对神经网络模型进行改进或替换,如用Transformer 模型等;内存占用比传统模型高了20%～30%,比传统模型稍高,基本保持在同一水平;同时精度有显著提升.

表7 3 个算例的燃烧模型CFD 结果(时间消耗值、内存占用值及精度提升值)Table 7 CFD results of three cases under two combustion models (time consumption value,memory occupancy value,and accuracy improvement value)

5 结论

本文基于深度学习和人工神经网络开展了湍流燃烧模型研究,采用全连接神经网络,通过MSE 损失函数、Adam 优化器、ReLu 非线性激活函数和ReduceLROnPlateau 调制器生成了神经网络模型,代替了火焰面/进度变量数据库以实现高维参数建模及模型改进,并成功运行在GPU 上.分析发现人工神经网络模型训练前对训练集进行数据处理是必要的,采用归一化处理方法对不同量级的数据都实现无量纲化,统一评价准则,防止因净输入数据绝对值过大造成的神经元输出饱和情况;神经网络模型的精度大部分情况会随着神经元数量的增加而提高,但是训练模型精度的提升付出的代价是因为神经元数量增加而不断增大的模型文件,研究确定选择各层神经元数量为10,20,40,20,10;采用第1 层神经元数量为10 时,选择MSE 损失函数比Huber 损失函数更好;优化器配合学习率调制器对于ANN 模型的训练收敛速度和精度提高有显著作用,学习率调制器弥补了Adam 后期收敛速度过慢的问题.最后,基于新一代宽速域高超声速飞行器Ma4～12 范围内的3 个发动机燃烧算例开展了测试分析,对误差进行了详细的分析,包括了对应每个算例每一实验点的误差值和总体误差值.结果表明智能化改进的模型比传统的模型平均误差减小量均超过了50%,算例误差最大减小值可达57.2%.