平台运动对柔性立管涡激振动影响的实验研究1)

朱红钧 刘文丽 高 岳

(西南石油大学油气藏地质及开发工程国家重点实验室,成都 610500)

引言

当前,新能源大规模开发与并网利用技术还不够成熟,常规化石能源与新能源“双能驱动”、“有序替代”是顺利实现“双碳”目标的主要路径.海洋油气资源是能源保供的重要支撑,作为连接海底管道与水面平台的油气输送纽带,海洋立管在海流激励下存在涡激振动(vortex-induced vibration,VIV)与顶部平台涡激运动(vortex-induced motion,VIM)的耦联响应,易发生疲劳损伤.为预测其服役寿命,近年来,大量学者开展了海洋立管的涡激振动响应研究,运用数值分析与实验测试手段从海流速度剖面、立管布置形式、端部约束条件等方面进行了系统分析.相较于短直刚性立管,柔性立管因变形与空间振动的差异性使其响应更为复杂.

文献[1-3]的研究发现柔性立管VIV 由多个频率参与,引起管轴方向振动传递的行波效应,振动的空间非对称性较明显,且轨迹偏离简单的圆或八字形,呈现典型的非周期性,这与Bourguet 等[4-5]发现的非线性剪切流诱导的柔性立管振动行为吻合.Vandiver 等[6]的实验研究亦发现了多频-多模态竞争的现象,这在Zhu 等[7-8]开展的悬链线柔性立管振动实验中得到证实,他们指出振动主导频率沿立管轴向空间和随时间的变化体现了空间的模态竞争和时间的模态切换,且这种多模态振动响应在模态过渡组次更为明显.Gedikli 等[9]研究发现流向振动的模态切换与横向振动有关,表明两个方向的振动存在耦合效应.但Kim 等[10]和Fan 等[11]通过实验和模拟发现立管横向振动由多频参与,沿管轴传递呈行波特征,而流向振动频率相对单一,沿管轴传递呈驻波特征,表明两个方向的振动并不同步,存在空间上的差异.

柔性立管的顶端连接至浮式平台底部,受平台VIM 的影响,立管顶部为动边界.部分学者开展了顶部铰接-底部固定的直立柔性立管VIV 研究.Seyed-Aghazadeh 等[12]实验对比了不同边界约束的立管振动,指出边界条件主要影响了流向振动的幅度与频率.Gao 等[13]通过数值预测发现,当立管长径比大于200 时,振幅、频率及频带受端部边界条件的影响减小.Gonzalez[14]开展了小尺寸船舶运动诱导的VIV 实验,当顶部运动频率接近立管固有频率时,观察到了共振现象.Chen 等[15]运用有限元方法数值预测了顶端垂直运动对柔性立管VIV 的影响,发现振动位移比顶端固定时增长了几倍.Wang 等[16-17]对存在顶部激励的悬链线型立管开展了模型实验研究,分析了顶部激励Keulegan–Carpenter (KC)数对立管振动的影响,观测到振动沿管轴传递至端部时出现反射波和驻波.付博文等[18]基于切片理论开展了平台横荡运动时柔性立管的VIV 模拟,并与Wang等[19]的实验结果进行了对比,发现顺流向振动主要包括低频振动、立管转向时引起的一阶振动和泄涡引起的二阶振动3 种形式,而横流向振动存在初始分支、振动锁定分支和去同步化分支.

事实上,平台-立管系统为一个整体,柔性立管的VIV 和平台的VIM 都是受到来流作用同时产生的.目前,同时考虑平台纵荡和横荡运动对悬链线型柔性立管VIV 响应的实验研究还较少,平台的VIM 和柔性立管的VIV 之间的相互作用尚不明晰.因此,本文开展了平台-立管系统在海流作用下的耦合响应实验研究,旨在剖析两者之间的耦联关系以及平台运动对立管平面内振动、平面外振动耦合响应的影响.

1 实验方法

1.1 实验布置

本实验在西南石油大学自循环实验水槽中开展,水槽测试段为2 m (长)×0.5 m (宽)×1 m (高),实验水深为0.65 m.实验采用概化模型,装置布置如图1 所示,选用外径D=8 mm (壁厚1 mm)的透明硅胶管作为柔性立管模型,长径比l/D=125,以悬链线型布置于水槽测试段,底部固定于水槽底壁,顶部铰接于平台底部,立管凹面迎流,布置垂高h=0.65 m.立管完全浸没于水中,横向阻塞率为1.6%,满足小于5%的临界阻塞率要求.

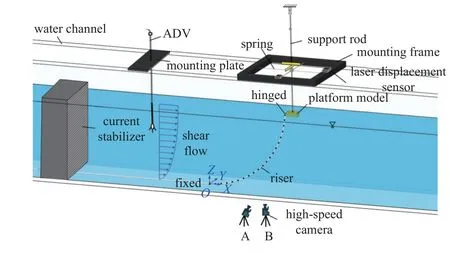
图1 实验布置示意图Fig.1 Schematic diagram of the experimental set-up

上部平台模型为93 mm (长)×52 mm (宽)×40 mm (高)的长方体,吊装于悬臂支撑杆底部,悬臂支撑杆由弹簧支撑,以约束平台在水平面两个自由度运动(纵荡和横荡).静水时,平台下部浸没高度为10 mm.

1.2 测试方法

水槽上游布置有整流排管,上游来流整流后在水槽内发展为对数剪切流,其速度剖面由布置于立管上游1 m 处的超声波多普勒测速仪测得,图2 显示了代表性组次(18 组中的8 组)的速度剖面,其流速剖面公式为[20]

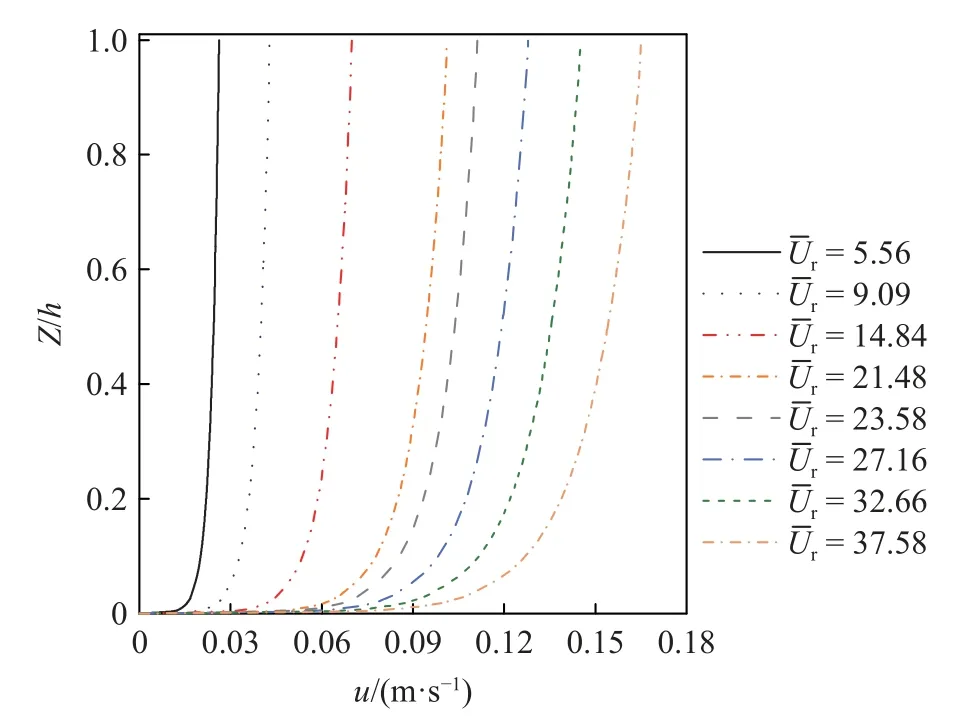
图2 来流速度剖面Fig.2 The oncoming flow velocity profiles

式中,u*为摩阻流速,u是与深度相关的流速,k是von Karman 常数(k=0.412),Z是距水箱底部的垂直高度,υ为水的运动黏度.因不同水深处的来流速度有别,为了区别实验组次,定义沿水深的平均约化速度为

实验采用非介入光学测试手段,由两个激光位移传感器分别监测上部平台纵荡和横荡位移,由两台高速摄像机分别监测柔性立管平面内与平面外的振动位移,该测试方法已在前期柔性立管涡激振动、段塞内流流致振动实验中成功运用,其测试流程与误差分析详见参考文献[21-31].为给高速摄像机提供跟踪对象,沿柔性立管轴向均匀标记了30 个黑色标记圈,每个标记圈的宽度为6 mm,相邻两个标记圈的中心间距为26 mm.如图3 所示,位于水槽侧面的高速摄像机(camera A) 捕捉立管平面内(XOZ面)的振动位移,位于水槽底部的高速摄像机(camera B)捕捉立管平面外(Y方向)的振动位移,高速摄像的监测频率为100 fps,与激光位移传感器同步触发.将拍摄的初始图像作为模板,由矩不变量描述各个标记圈的灰度信息,用于后续图像的比对识别.对记录的每一帧图像,依次定义空间坐标轴、关联每个标记圈所占像素单元数与实际尺寸、对比灰度信息识别标记圈位置、与初始图像对比得到平移的像素单元数,最终换算得到实际振动位移.将高速摄像机记录的图像按时序处理,得到各个标记圈的振动位移时程曲线,经滤波降噪后,通过快速傅里叶变换得到其振动频谱.

1.3 衰减实验

首先,在静水中对弹簧支撑的平台与铰接于平台下方的柔性立管整个系统进行自由振动衰减实验,以同时得到平台和立管的固有频率.测试时,沿某一向给平台施加一个初始位移后释放,监测平台在该方向的振动位移时程曲线,经快速傅里叶变换后得到该方向的固有频率.同理,对立管跨中施加平面内或平面外的初始位移,将位移衰减曲线快速傅里叶变换后得到对应的平面内或平面外的固有频率.如表1 所列,平台纵荡和横荡的固有频率相等,为fpx=fpy=0.87 Hz,下文统一记为fp;立管平面内、平面外振动的前3 阶固有频率近似翻倍增长.表中下标i 和o 分别表示平面内和平面外,下标1,2,3 表示1 阶、2 阶、3 阶,上标w 表示静水.

表1 平台和立管的固有频率Table 1 The natural frequencies of platform and riser

2 实验结果分析与讨论

2.1 平台运动与立管振动的耦联效应

图4 为平台在X方向和Y方向的运动幅值及频率随约化速度的变化曲线.在附近,平台Y方向运动幅值较大,其余的运动幅值均较小.时,随着约化速度的增加,平台运动幅值呈小幅单调递增.时,X方向幅值大于Y方向幅值,表明高流速对流向运动的影响更显著.时,平台运动频率脱离其固有频率,表明立管振动对平台运动的影响,而在其他约化速度范围,呈涡激运动锁定现象[32].

图4 平台运动振幅及主导频率Fig.4 Schematic diagram of the image post-processing method

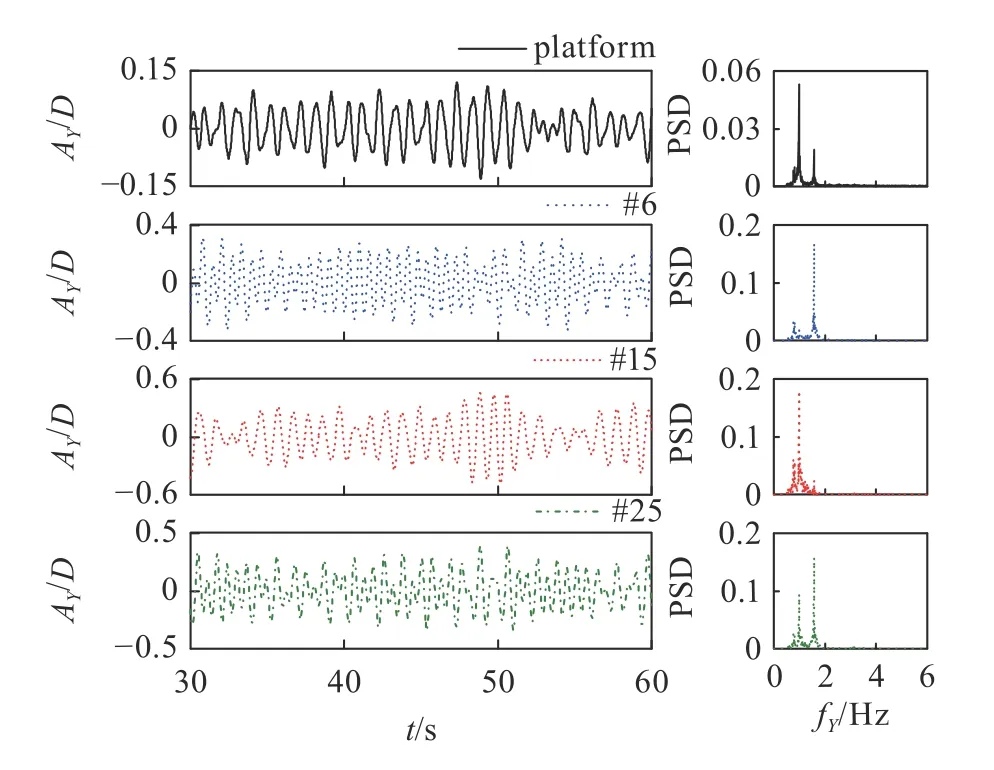
图5 典型约化速度时平台运动与立管代表性标记圈的时程曲线及振动频率Fig.5 Time history of the response amplitudes of the platform and representative markers of the riser and associated frequency spectra at typical reduced velocities

图6 展示了6 组代表性约化速度的立管振动频率沿管轴的分布,第1 行为平面外的振动频率,第2 行为平面内的振动频率,并在s/l=1.0 处(s为自立管底部至管道某一位置的轴向长度,l为立管长度)叠加显示了平台的运动频谱图,图中竖向虚线标注出平台和立管的固有频率.由图可见,当=7.31 时,立管平面外振动能量主要分布于两个频率,其中,高频接近立管平面外的2 阶固有频率,而低频位于平台的固有频率附近,存在频率的竞争现象.若立管振动的主导频率(能量占比最大的频率)与平台运动的主导频率相同,则称两者为强耦联(图中标记为strong coupling),其余管段部分称为弱耦联(图中标记为weak coupling).因立管振动的主导频率沿轴向改变,因而存在空间的频率竞争[6,10-12]和强弱耦联之间的切换现象.当时,立管平面外振动能量相对集中于其2 阶固有频率附近,表明此时的立管平面外振动由2 阶模态主导,而平台运动的主导频率也恰好与立管振动频率吻合,表现出强耦联关系.当增大到17.13 时,同时出现了一个接近平面外3 阶固有频率的高频,再次出现空间上的频率竞争现象,立管跨中部分由强耦联转变为弱耦联.当时,立管振动高频的能量占比增大,同时平台运动的主导频率也恢复至与其固有频率一致,故仅有立管顶部与平台强耦联,其余管段均为弱耦联关系.

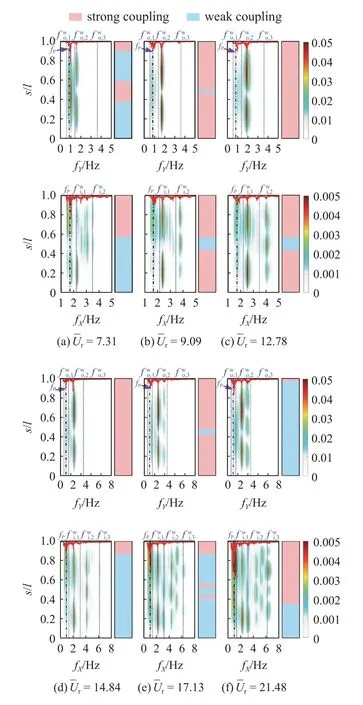
图6 典型约化速度时的平台运动与立管振动频率Fig.6 The frequencies of platform motion and riser vibration at representative reduced velocities

如图6 所示,立管平面内振动由更多的频率参与,其中低频位于平台固有频率附近,另外的振动频率随着约化速度的增大逐渐增大,且振动能量也逐渐向高频转移,体现了模态过渡过程,立管与平台强耦联的管段长度有明显减小.但在时,立管上半部分的主导振动频率与平台运动的主导频率重新吻合,因此上半部分为强耦联,下半部分为弱耦联.

为了更好地量化立管空间上与平台运动耦联的长度,从立管顶部向下将其振动主导频率与平台运动的主导频率相同的管长定义为强耦联长度lco,其随约化速度的变化情况如图7 所示,lco-PY和lco-PX表示立管平面外振动、平面内振动分别与平台运动强耦联的长度.由图可见,在低约化速度时,强耦联长度相对较大,而高约化速度时有一定的缩短.尤其是平面外振动,在高约化速度时,仅有与平台相连的立管顶部为强耦联,其余均为弱耦联,表明立管的平面外振动基本由自身的模态主导,受平台运动的影响较小.在模态过渡组次,强耦联长度相对较短,证明立管自身模态竞争强烈时也影响到了其与平台运动的耦联强度.平台运动与立管振动存在两个方向均耦联(简称双向耦联)、仅单一方向耦联(简称单向耦联)和不耦联3 种情形.在<20 时,双向耦联长度较长.立管振动处于模态过渡时,双向耦联长度缩短.≥20 时,平台运动与立管振动大部分为单向耦联.由图8 可见,立管轴向呈现双向耦联、单向耦联及不耦联的部位,相应的三维振动轨迹亦不相同.

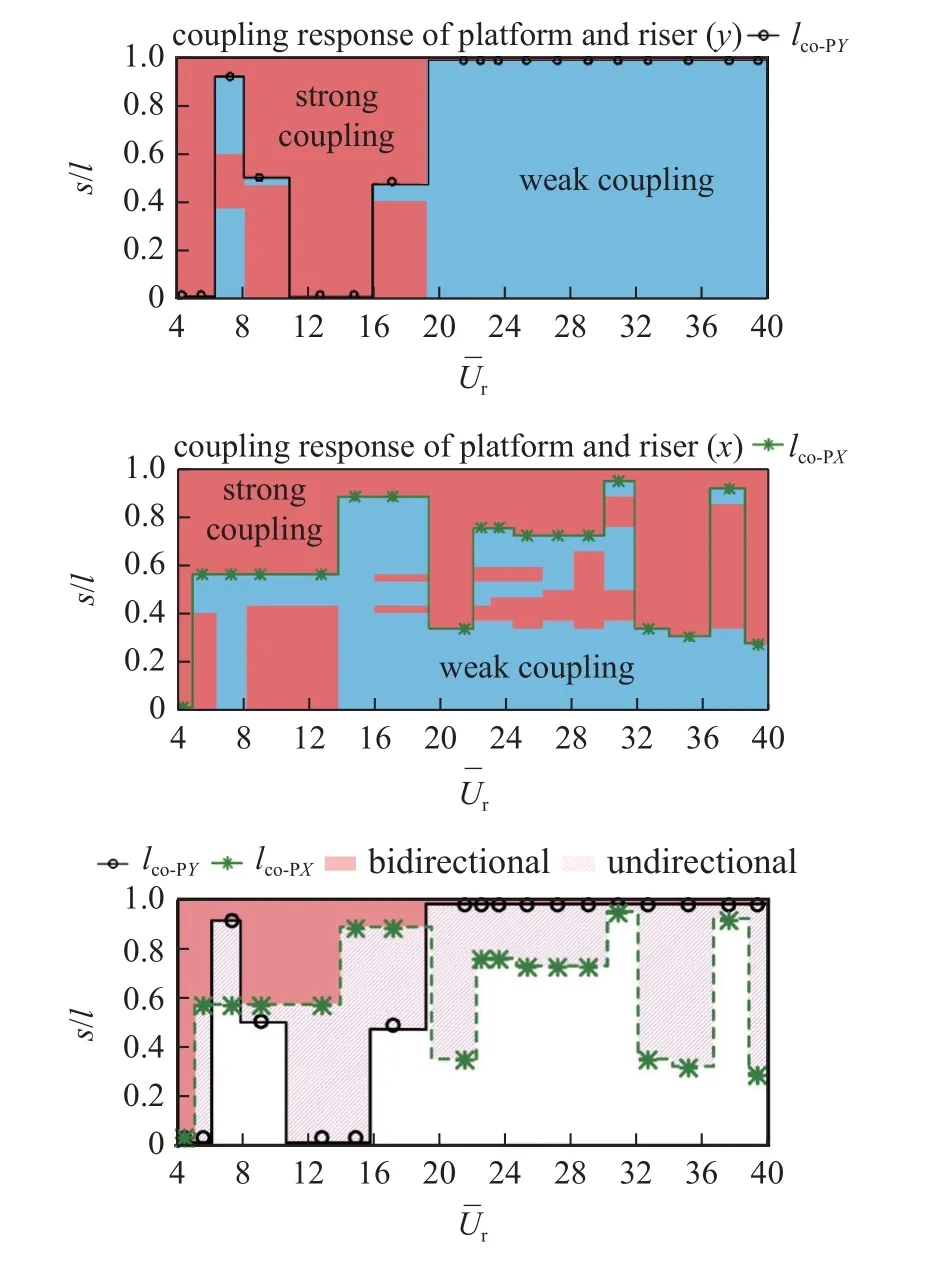
图7 与平台运动耦联的立管长度Fig.7 The length of riser coupled with platform motion

图8 =17.13 时,立管振动三维包络图及不同耦联模式的三维轨迹图Fig.8 The envelope of riser vibration and trajectories of different coupling modes at =17.13

图9 对比了过滤平台固有频率fp(因fp参与了立管振动)前后的立管均方根振幅,过滤前后立管振幅大小有一定的区别,但均方根振幅曲线的波峰个数并未改变,即过滤平台的固有频率不会改变立管振动的主导模态.在高约化速度(≥24),过滤前后的立管平面内流向(X方向)振幅差别较明显,尤以立管上部为甚.由于此时平台运动频率锁定于其固有频率,将其过滤后影响了立管上部的振幅分布,进一步证明了此时立管上部振动与平台运动强耦联.

图10 对比了几个典型约化速度时过滤平台固有频率前后的立管振动主导频率的时空分布.约化速度较低时(=12.78,14.84),过滤平台固有频率前后的区别主要体现于立管顶部,而其余部分的立管振动主导频率时空分布没有明显变化,这是由于平台运动的主导频率与立管振动的主导频率吻合(见图6),远离平台自身的固有频率,将其过滤并无太大区别.=17.13 时,立管平面内X方向振动的主导频率在过滤了平台固有频率后出现了较明显的区别,主要体现在跨中的主导频率由间歇性切换转变为连续稳定变化.当≥21.48 时,平台运动频率与其固有频率吻合,将其过滤后,立管更多管段出现了不同的X方向振动主导频率,体现了空间的频率竞争现象,表明高约化速度时,平台运动抑制了立管空间的频率竞争.相较于平面内X方向振动,平面外振动在过滤平台固有频率前后的变化不明显,表明平面外振动受平台运动的影响相对较小.

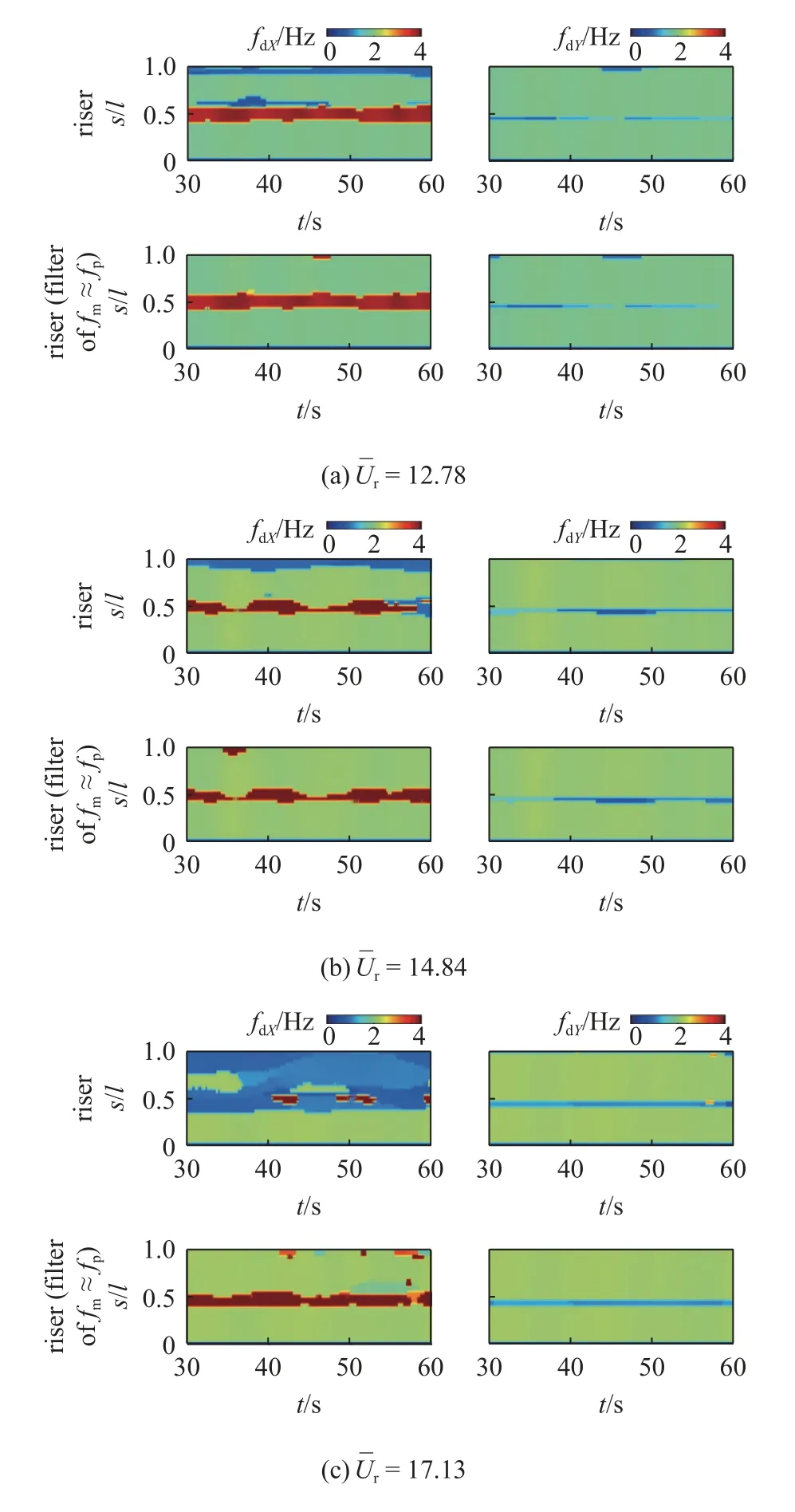
图10 过滤平台固有频率前后的立管振动主导频率的时空分布对比Fig.10 Comparison of the spatial-temporal evolution of the dominant frequency before and after filtering out the natural frequency of platform

2.2 平台运动引起的立管瞬时形态变化

运动的平台给立管顶部施加了动边界,可能引起立管局部弯曲,从而改变立管瞬时振形的波腹个数或节点个数.如图11 为=21.48 时立管瞬时振形的波腹个数Np随时间的变化,可见其在2,3,4 和5 几个数值间切换.在时间窗口I,平台向X负向运动,立管上部的负向位移随着时间的延长逐渐增大,与平台运动同向;而立管中下部处于正向位移的管段(绿色底色标注)运动速度快速减小,快于其两侧的管段,因而造成立管瞬时振形增加两个节点,Np由2 跃升至4.在时间窗口Ⅱ,平台运动方向与立管顶部振动方向相反,因而造成立管顶部新增一个弯曲段(绿色底色标注),Np由4 变为5.在时间窗口Ⅲ,平台向X正向运动,立管中上部的运动速度变化较立管上部小,引起中上部出现新的弯曲段(绿色底色标注),Np由3 增为4.在时间窗口Ⅳ,平台向X正向运动,立管运动速度快于平台,造成节点数的减小,Np由4 降至2.在时间窗口V,平台向X负向运动,立管上部运动速度快于平台,造成节点数的减小,Np由4 降至3.与时间窗口V 相同,在时间窗口Ⅵ,立管中上部运动速度快于平台,造成节点数的减小,Np由5 降至3.因此,平台与立管的运动速度、运动方向是决定立管瞬时振形是否改变的主要因素.

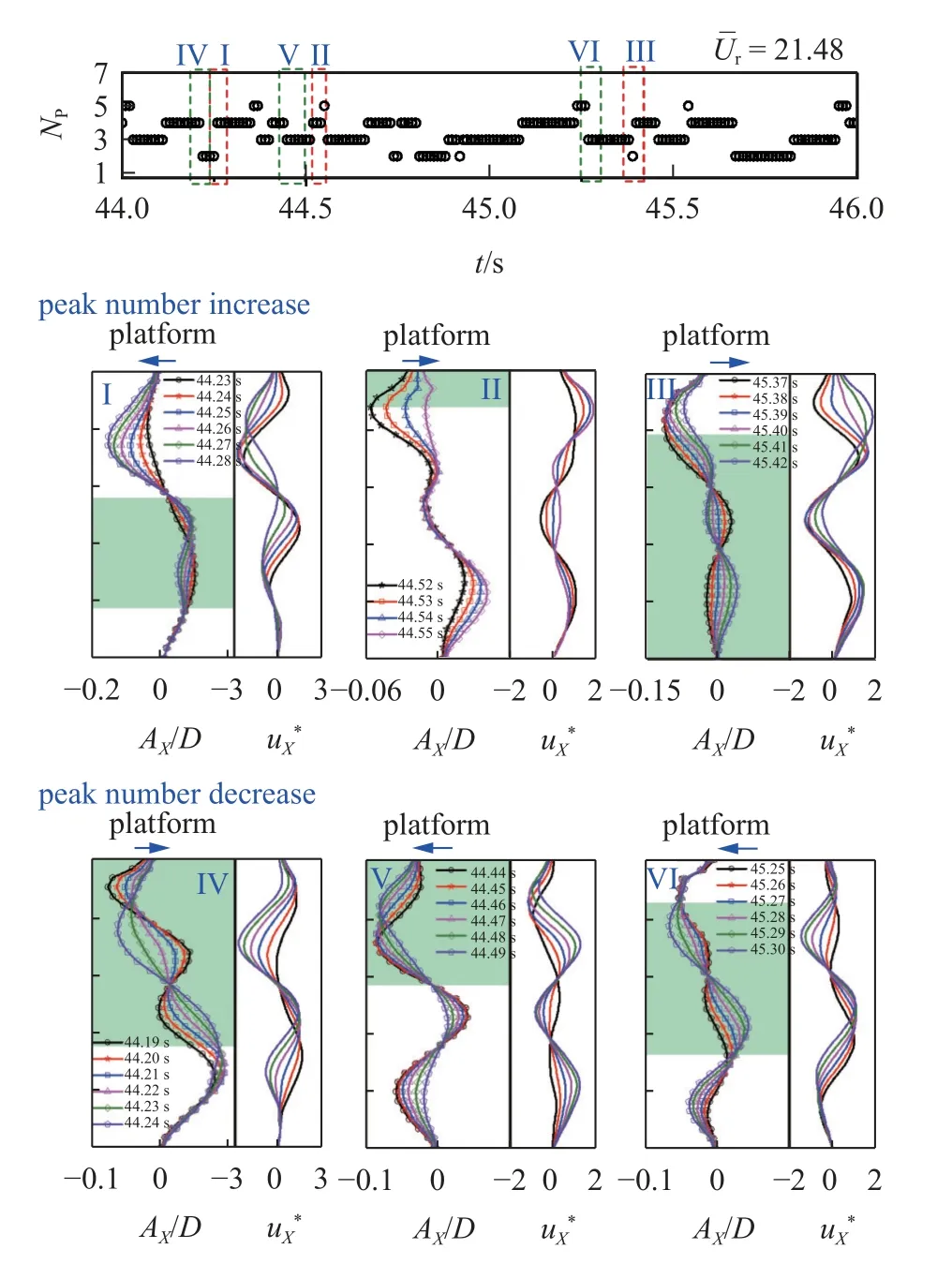
图11 平台运动对立管瞬时振形的影响Fig.11 The influence of platform motion on the instantaneous shape of riser

由于立管振动处于模态过渡组次时由多个模态参与竞争,相应的模态振形也会交替出现,因此有必要区分平台运动引起的振形变化和模态竞争造成的振形改变.图12 选择了6 个代表性约化速度,展示了瞬时振形、Np、参与振动的频率权重随时间的变化.=12.78 时,立管振动以1 阶频率为主,2 阶频率权重约为20%,存在1 阶和2 阶模态竞争.若立管两端固定,Np应以2 为主,间隙性出现3,但实际上大部分时间Np=3,间隙性出现2,4,5,表明平台运动改变了立管振形.将Np=2 的时间占比记为立管本身振动的贡献,约14.4%,而其余时间段认为受到平台运动的影响,占85.6%.=14.84 时,立管主要以一阶频率振动,但Np并不等于2,而是出现了1,3,4,5,6 等数值,表明平台运动显著改变了立管振形,其贡献的时间占比约为100%.=17.13 时,一阶频率fx1与平台固有频率fp共同参与了立管振动响应,除Np=2 外,其余数值均表明受到了平台运动的影响,贡献的时间占比约为91.1%.=21.48 时,立管振动以二阶频率和平台固有频率为主,Np=2,3视为两者竞争的贡献,而Np=4,5 为平台运动的贡献,其时间占比约为43.85%.同理,=27.16,35.12 时,由平台运动改变了立管振形的时间占比分别为87.1%和72.1%.

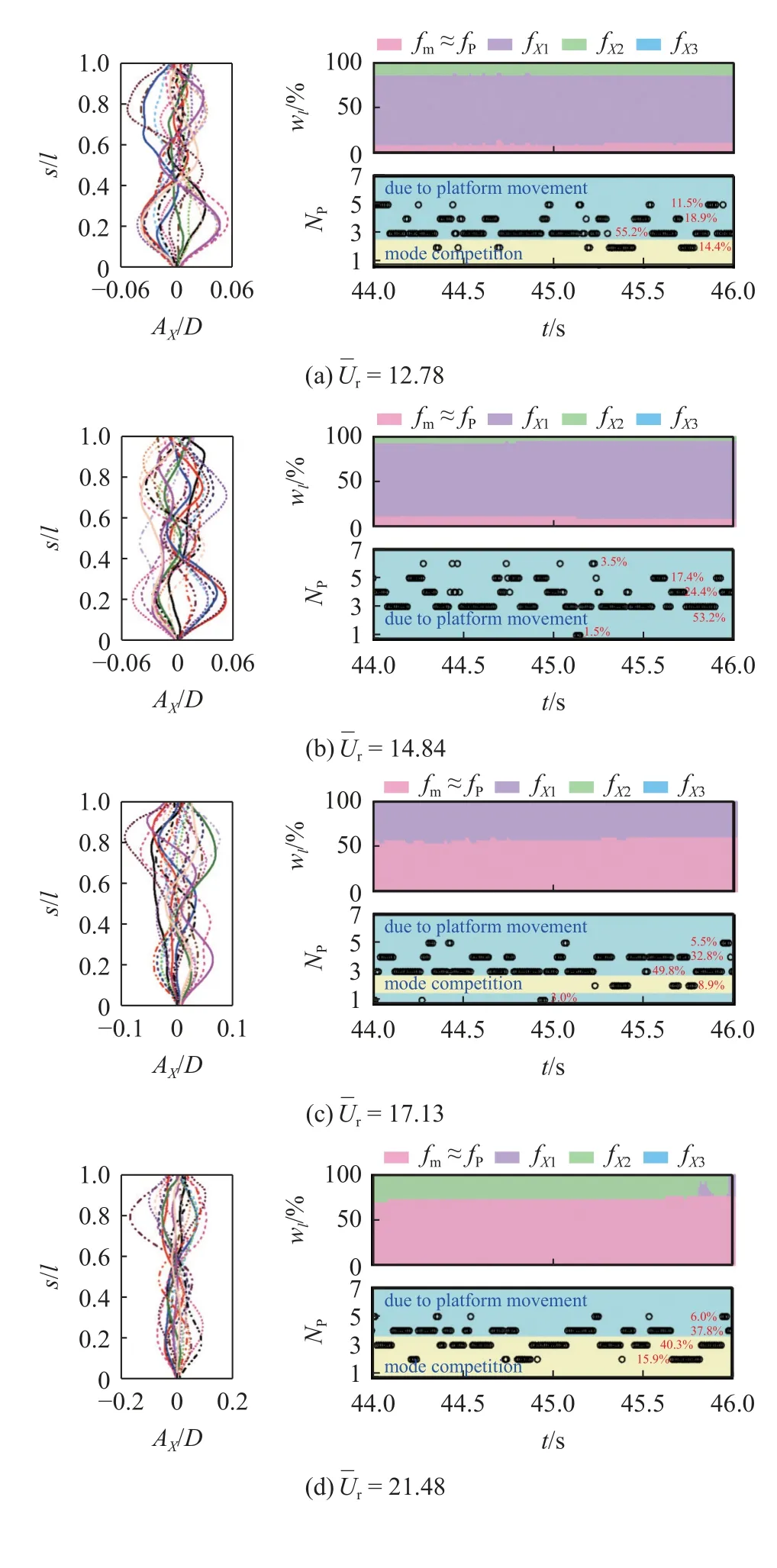
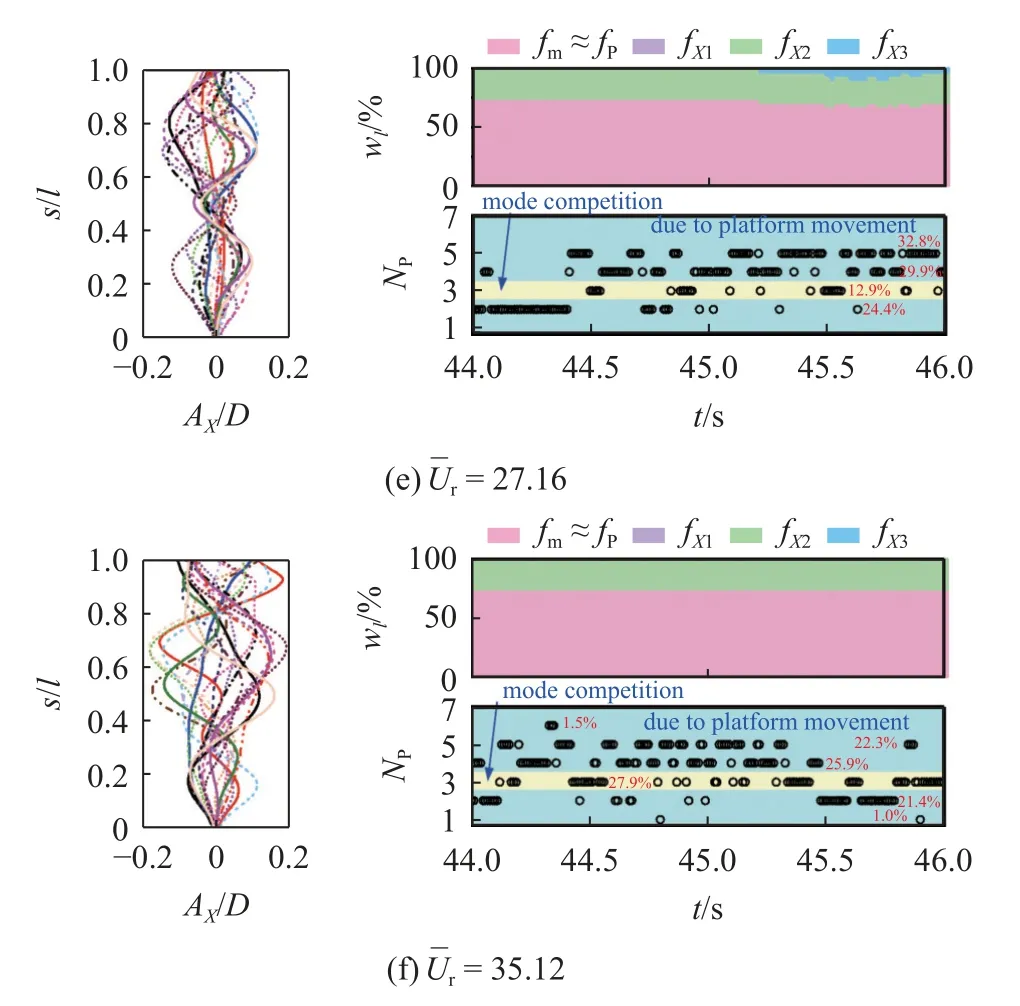
图12 平台运动与模态竞争对立管瞬时振形的贡献Fig.12 The contributions of platform motion and mode competition to the instantaneous shape of riser

2.3 立管平面内外耦合响应

除了平台运动与立管振动之间存在耦联外,立管平面内与平面外两个方向的振动之间也存在着耦合关系.图13 以=30.84 时的立管平面内与平面外振动主导频率分布为例,演示了如何获取两者强耦合的时间权重与强耦合的空间长度.图中fdX为平面内X向主导振动频率,fdY为平面外主导振动频率,fdX/fdY=1 意味着两者同频,视为强耦合,其在空间的分布和随时间的波动可以由fdX/fdY=1 的时空分布图给出,由此可以统计出沿管轴不同位置出现强耦合的时间百分比(wt)和出现强耦合的管长占比随时间的变化(wlxy).

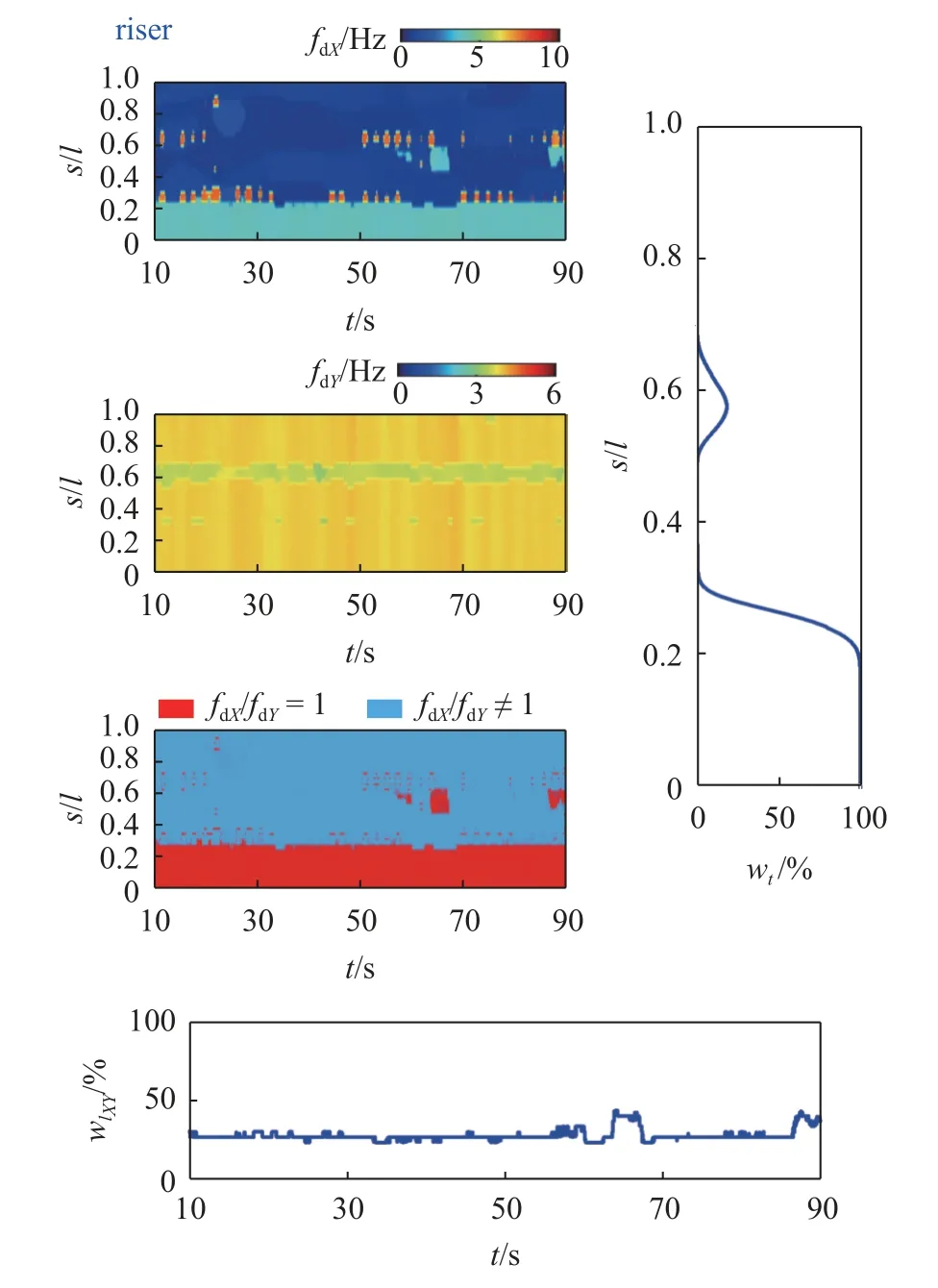
图13 强耦合时间占比与强耦合长度的获取示意图Fig.13 Schematic diagram of the obtainment of the time weight of strong coupling and the coupling length

(1)强耦合时间权重的计算:对于立管空间上某点,该点X和Y方向的振动主导频率均随时间变化.故选取振动时长80 s,两个方向的拍摄图片各8000 张(拍摄时间为0.01 spf)各有8000 个按时序排列的频率数据,当两个方向的振动主导频率相近(±10%)称为强耦合,若其个数为N,则两个方向强耦合的时间权重记为wt(%)=N/8000×100%.将立管30 个标记点数据沿轴向分布绘制,则得到强耦合时间权重沿立管轴向的变化.

(2)强耦合空间权重的计算:在某一瞬时,立管轴向30 个标记点有各自的振动主导频率.对于一个标记点而言,当X和Y方向的振动主导频率相近(±10%)称为强耦合.若强耦合的标记点个数为N,则该时刻强耦合空间长度为wlxy(%)=N/30×100%.该空间耦合长度随时间的变化而改变.

图14 对比了6 个典型约化速度在过滤平台固有频率fp前后的wt和wlxy.≥17.13 时,过滤fp后的wlxy明显增大,且随时间的波动增强,表明平台运动抑制了立管平面内与平面外的耦合响应.对于wt而言,过滤fp前后的立管上部变化最显著,证明立管上部受平台运动的影响最大.此外,在≥17.13 时,过滤fp后的立管中部wt亦明显增大,表明平台运动对立管中上部的平面内外耦合响应起到了抑制作用.而抑制作用在高约化速度时更加明显,这与平台在高约化速度时的运动位移增大有关.

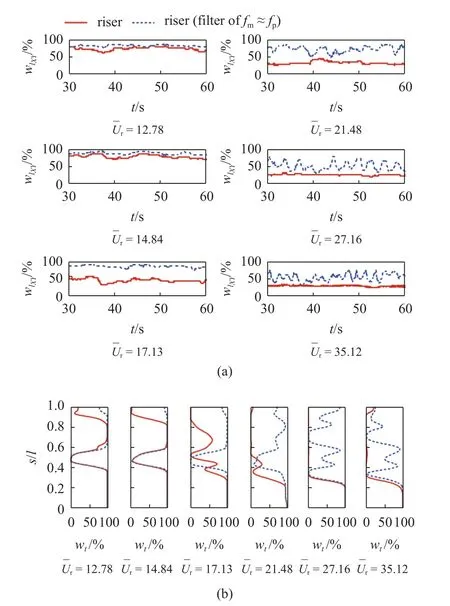
图14 (a)强耦合长度随时间的脉动和(b)强耦合时间占比的空间分布Fig.14 (a) The variation of strong coupling length over time and(b) spatial distribution of the time weight of strong coupling

3 结论

本文基于自循环实验水槽研究分析了雷诺数为150～1330,速度为4.40～39.33 围内的平台纵荡和横荡运动对悬链线型柔性立管涡激振动的影响,得到主要结论如下.

(1) 在立管振动频谱中发现了平台运动频率,在平台运动频谱中也存在立管振动频率,体现了两者的耦联效应.将平台运动主导频率与立管振动主导频率相同时定义为强耦联,其余为弱耦联.因立管振动的主导频率存在空间竞争,因而强弱耦联也存在空间切换,故定义了强耦联长度.模态过渡组次的强耦联长度相对较短,在低约化速度时,平台与立管平面外耦联长度约占100%,高约化速度时立管平面外振动受平台运动的影响较平面内振动小.

(2) 过滤平台固有频率后,立管平面内振动在高约化速度时的变化较显著,体现出振幅的减小和频率竞争现象的增强,说明平台运动抑制了立管空间的频率竞争.对比沿管轴不同位置出现平面内、外强耦合的时间占比和出现强耦合管长占比随时间的变化,立管上部受平台运动影响,平面内外耦合时间占比存在较大波动,立管下部耦合时间占比为100%,在高约化速度时,平台运动对立管平面内、外耦合响应起抑制作用.

(3) 平台与立管的运动速度、运动方向是影响立管振动形态的主要因素,以立管瞬时形态的波腹个数变化量化了模态竞争和平台运动对振动形态的影响.在=27.16,35.12 时,由平台运动改变了立管振形的时间占比分别为87.1%和72.1%.模态竞争较弱的组次,立管振形受平台运动的影响较大.

数据可用性声明(Data availability statement)

支撑本研究的科学数据已在中国科学院科学数据银行(Science Data Bank) ScienceDB 平台公开发布,访问地址为https://www.doi.org/10.57760/sciencedb.j00140.00024.