质量比对D 形截面柱体流致振动的影响1)
2024-04-15宋吉宁蒋学炼金瑞佳刘宇航
宋吉宁 李 壮 蒋学炼 金瑞佳 刘宇航
* (天津城建大学天津市软土特性与工程环境重点实验室,天津 300384)
† (交通运输部天津水运工程科学研究院,港口水工建筑技术国家工程研究中心,天津 300456)
引言
流致振动是一种复杂的流固耦合现象[1],广泛存在于海洋立管、海底管道、大跨桥梁结构等工程领域中,可导致结构疲劳破坏.已有的研究大多关注于认识和抑制结构的流致振动,减少流致振动所带来的危害[2-4].近年来,随着绿色能源开发研究的发展,利用流致振动实现海流能俘获也引起了学者们的关注[5-9],具有代表性的是Bertinsas 等[10-11]开发了一种低速海流发电装置(VIVACE)进行海流能的捕获,此装置可将柱体振动的机械能转化为电能,具有启动流速低、简单易维护、对海洋环境好、不影响通行等潜在优势.关于海流流致振动和海流能能量转化的研究,练继建等[12]梳理了柱体流致振动的研究现状并剖析其中存在的问题,建议可利用流致振动进行新型能源的开发.
在柱体流致振动和能量捕获的研究中,大多数是关于圆形截面柱体的[13],及春宁等[14]和殷布泽等[15]对圆柱形的研究进行了综述.Williamson 等[16-18]开展模型实验研究了低质量比圆柱的涡激振动特性,发现振幅与整个系统的质量阻尼比(m∗ξ)有关.宋吉宁等[19]使用拖曳装置在均匀流条件下对柔性立管进行涡激振动实验,发现在均匀流条件下,立管仍存在多模态振动,顺流向主导模态则多达12 个.陈正寿等[20]针对质量比开展了刚性圆柱的数值模拟,发现质量比是影响圆柱体振幅的一个重要因素.唐国强等[21]发现在低雷诺数下,当串联的柱体距壁面的距离/柱径为0.25 时,柱体的尾涡脱落被抑制,柱体不发生振动.刘旭菲等[22]对不同质量比的圆柱进行了近壁面涡激振动的数值模拟.发现随着质量比的增大,近壁面圆柱的振动在高折合速度下才会发生,振幅也较小,且受到壁面边界层的影响,低质量比柱体在顺流向和横流向的振动频率相等.在能量俘获效率方面,白旭等[23]发现圆柱体的获能效率与柱体振幅的大小并没有直接的关系,柱体的振幅越大,获能效率不一定越高.
已有研究表明,不同的截面形状对柱体流致振动有重要影响[24].李海涛等[25]通过实验和CFD 的方法研究了不同截面下钝头体及宽厚比对流致振动能量收集特性的影响,发现钝头体为D 形截面时,流致振动呈现“涡激振动”“涡激振动-驰振”和“驰振”的变化.
在非圆形截面中,由一个平面和一个半圆的曲面组成的D 形截面柱体(图1)是比较有代表性的一种.关于D 形截面柱体流致振动的研究,部分是通过风洞试验[26],然而由于空气和水在密度和黏性方面差异较大,柱体在水中的流致振动与风洞实验中存在较大差异.Zhao 等[27]通过水槽实验研究了质量比为6 时D 形截面柱体的流致振动响应,D 形的直边分为迎着或背向来流方向两种状态,并指出没有后体也可以发生涡激振动.Chen 等[28]开展了低雷诺数100 时,质量比为2 时单自由度D 形截面柱体横流向流致振动的数值模拟,分析了不同迎流攻角、涡激振动与驰振的特性.卫昱含[29]结合高斯过程回归方法分别对质量比为2 的迎流攻角0°和180°的D 形截面双柱体进行数值模拟发现,柱体的振幅和能量利用效率无必然联系,角度和阻尼比对能量利用效率影响显著.Li 等[30]设计了ODO,ODODO 和DOD 三种不同排列的柱体,研究截面变化对涡激振动能量收集的影响.结果表明,D 形截面柱体夹在两个圆形截面柱体之间时,柱体的振动受到抑制;而其余两种排列的柱体可以增强涡激振动,并且增大锁定区间,提高了能量转化效率.

图1 D 形截面柱体布置图Fig.1 Schematic of D-section prism
上述研究表明,关于不同质量比下D 形截面柱体流致振动响应及其尾流特性的认识尚未完善,诸如响应特征、尾涡脱落形态、能量转化效率等特性或规律尚需进一步研究.因此,本文通过数值模拟研究四个不同质量比(2,5,7 和10) D 形截面柱体的流致振动问题.在雷诺数范围为288~2880,约化速度范围为2~20 的条件下,分析柱体横流向振动响应、频率响应、脱涡模式以及能量转化效率等规律特性,以期为海流能开发利用相关工程应用提供参考数据.
1 数值模型与计算方法
1.1 数值模型
在流场中放置一个D 形截面柱体,如图1 所示圆弧面向下,直边与水流方向平行,其直边长度DL为0.0381 m,迎流角度 α (见图1)固定为 90◦.为了探究柱体在横流向的最大振幅,忽略阻尼的影响,设阻尼比 ξ=0.选取了四个质量比m∗=m/md,分别是2,5,7 和10,研究D 形截面柱体在均匀来流U下的横流向振动特性.柱体在静水中的固有频率设置为fn=0.4 Hz,柱体在迎流面的特征长度De(De=0.5(1+|cosα|)DL) 取迎流面投影最大宽度,为0.01905 m.
计算域的参数设置,如图2 所示,坐标原点位于D 形截面柱体直边长度的中点处,x轴正方向为顺流方向,y轴则垂直于来流方向.流场计算域的顺流向总长度为48DL,横流向总宽度为24DL,柱体直边中心距离上下两侧边界及入口边界均设置为12DL,阻塞率为2.08%,小于5%可以忽略流场宽度对柱体振动的影响[31].
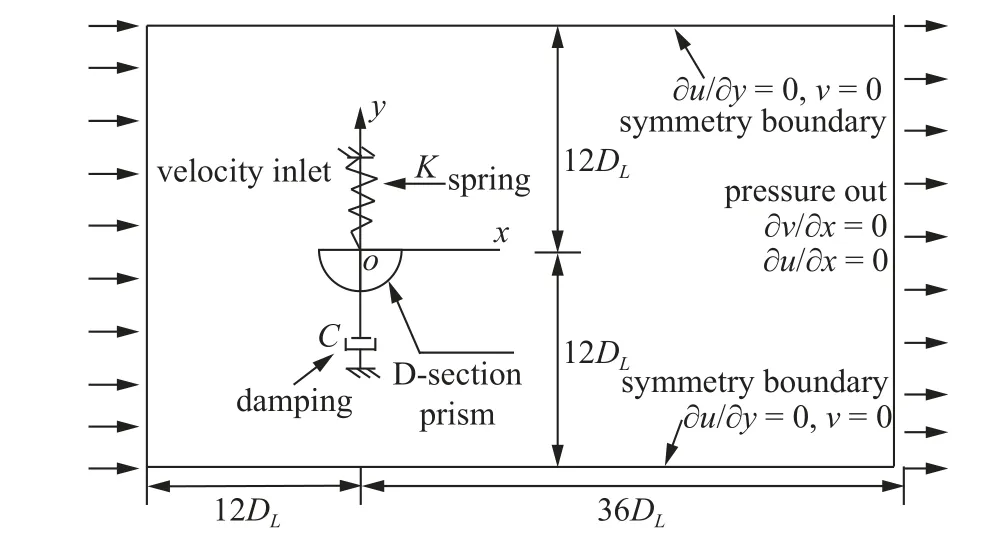
图2 计算区域与边界条件设置Fig.2 Computational domain and boundary conditions
本文所模拟的雷诺数范围为288 ≤Re≤2880,入口流速为恒定流.出口采用压力出口的边界条件,上下两侧边界设置为对称边界条件,柱体表面设置为无滑移壁面.
本文基于二维非定常不可压缩流体RANS 方程,采用ANSYS FLUENT 软件,应用k-ω SST 湍流模型,SIMPLEC 方法求解压力速度耦合方程,压力项采用PRESTO 方法离散[32],时间项采用QUICK方法离散,湍流动能项求解采用二阶迎风格式,比耗散率项求解采用一阶迎风格式,瞬态项采用二阶隐式求解方法,各个参数的收敛残差设置为1.0×10-5,最大迭代步数设置为30 步.
1.2 柱体结构运动计算方法
本文仅研究柱体在横流向上的振动响应,因此,流致振动的系统可以看作是一个单自由度的弹簧-质量-阻尼模型(图2),其在横流向的结构动力学方程为
式中,y为柱体中心在横流向的位置,m,c,k分别为系统的质量、阻尼和弹簧刚度.其中弹簧刚度k=,ω0为系统的圆频率.阻尼,ξ 为系统的阻尼比.Fy(t) 为柱体在横流向的阻力和升力.
柱体运动方程求解采用Newmark-β法,计算出每一个时间步后柱体新的位置、速度及加速度.需要注意的是,应用FLUENT 软件对柱体边界上的网格节点进行更新时,UDF (用户自定义函数)设置中不能将柱体新时刻的速度直接传递给柱体边界网格,即vel[1]≠y(t+∆t) .否则,将会造成新时刻柱体边界网格的位置与柱体位置出现偏差[33].根据Newmark-β法已知t时刻柱体的位置,则t+∆t时刻柱体的位置为
式中,yt+∆t为柱体t+∆t时刻位置,yt为柱体t时刻位置.∆t为时间步长.根据Newmark-β法无条件稳定的假设,β 一般取0.25,则式(2)中t+∆t时刻的柱体的位置为
通过DEFINE_CG_MOTION 宏,可将UDF 中计算出柱体在t+∆t时刻的速度,传回FLUENT 对柱体位置进行更新.根据软件手册,FLUENT 使用下式对网格节点位置进行更新
比较式(5)和式(3),发现柱体边界上网格位置与柱体位置的二阶项存在差异,这会导致两者位移不同步.因此,需要在UDF 中对新时刻柱体边界网格节点速度计算进行修正,采用式(6)
将上式代入(4),得到柱体边界网格节点在新时刻t+∆t时的位置为
比较式(7)与式(3),每次时间步更新后,柱体边界网格节点的位移与柱体是一致的.这表明采用式(7)更新柱体边界网格节点的新时刻速度,可以保证柱体边界网格与柱体位移同步,以获得更精确的数据.
1.3 能量转化效率
在水流作用下D 形截面柱体吸收流体能量产生运动,在一个周期T中,柱体俘能功率可以表达式为[34]
式中,m为柱体的质量,为柱体在横流向上的速度.流体扫过D 形截面柱体的能量可以表示为
其中,L为柱体的长度,U为来流速度,DL为D 形截面柱体直边长度.则一级能量转化效率 η 可以表示为
1.4 网格划分及网格独立性验证
D 形截面柱体的流致振动特性复杂,为了精确捕捉D 形截面柱体周围及尾部的流动特征,采用结构化网格剖分计算域(图3),将流体域划分为9 个部分,D 形截面柱体附近6 倍直径DL的范围采用“O 形切分”,近壁面进行局部加密,使得y+<0.6,y是从第一层网格中心到柱体壁面的距离,τw是圆柱壁面的剪切应力,µ 是动力黏性系数,ρ 是流体的密度).
为验证网格无关性,对比了5 组不同疏密的网格设置.在约化速度Ur=5,m∗=2.6,fn=0.4 Hz,ξ=0.003611 时计算D 形截面柱体的横流向响应振幅和频率.Mesh1~Mesh5 的主要区别是,逐次减小柱体周围6DL范围内的圆形加密区的网格增长率(数值见表1),可使得圆形加密区内的网格数量逐次增大,而离柱体较远区域的网格数量仅随之略有增多.总网格数量从2.6 万增至6.1 万.
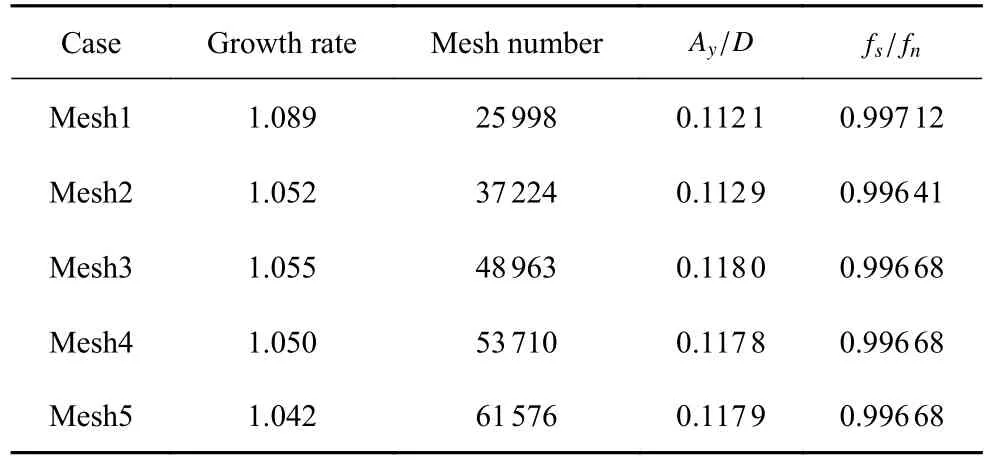
表1 网格独立性验证Table 1 Mesh independency study
表1 给出了5 种网格的计算结果,其中Ay/De为柱体无量纲横流向的均方根振幅(Ay=yrms),fs/fn为柱体振动频率与固有频率的比值.通过对比表1 的数据,在网格数量足够多的情况下,Mesh3,Mesh4 与网格Mesh5 相比,柱体的均方根振幅与振动频率的变化幅度均在1%以下.兼顾计算精度和效率,本文选择Mesh3 作为后续的计算网格.
为验证时间步长 ∆t的无关性,在U∆t/DL≤0.01的范围内,对比了5 个不同的时间步长的计算结果,具体参数见表2.算例参数同样采用约化速度Ur=5,m∗=2.6,fn=0.4 Hz,ξ=0.003611 时D 形截面柱体的横流向响应振幅和频率结果.从表2 可见,与最小的时间步长工况C1 相比,C4 的振幅偏差0.75%,频率偏差0.43%,相对偏差幅度都在1%以下,能够满足计算精确要求,兼顾计算效率考虑,本文选择将时间步长设为0.005 s.
2 数值模型验证
为了验证本文数值模型的可靠性,采用与D 形截面柱体流致振动实验相同的计算参数[27],柱体迎流角度为0°,且仅在横流向上振动,D 形截面柱体的直边长度DL=0.025 m,柱体的质量m=0.9018 kg,ξ=0.00151,在空气中的固有频率为fn,air=0.783 Hz,在水中的固有频率fn,water=0.74 Hz,附加质量为ma=((fn,air/fn,water)2-1)m.图4 比较了无量纲振幅(y10/DL)的数值结果和实验数据,其中y10表示柱体横流向的前10%最大振幅的平均值.从图中可以看到数值模拟柱体振动的幅值与实验值整体吻合较好,均随着约化速度的增加而增大,验证了本文数值模型的准确性.
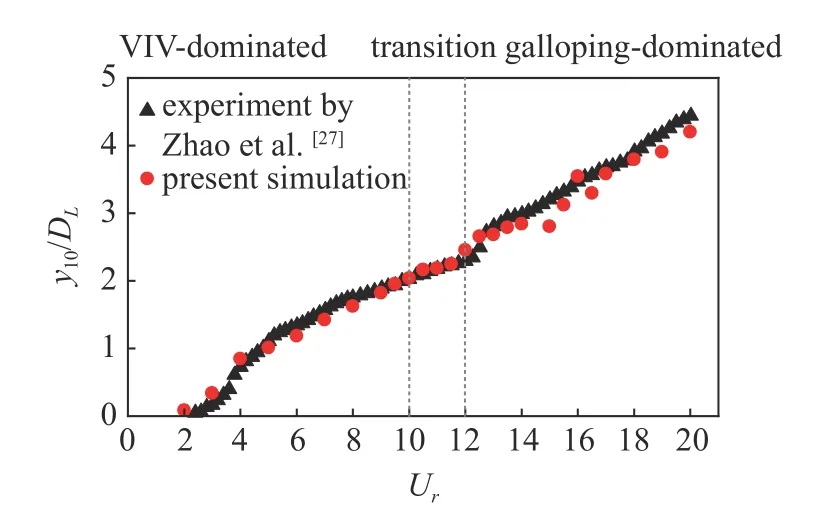
图4 响应振幅的对比Fig.4 Comparison of the vibration amplitude
3 数值计算结果与分析
3.1 振幅响应
在水流作用下,D 形截面柱体横流向振动的平衡位置逐渐脱离了柱体静止时的位置,因此采用柱体振动的平衡位置偏移量[35]和振幅[36]两者结合进行对比分析.|y0| 为柱体振动时振动平衡位置的偏移量.从图5 可以看到,当柱体的质量比为m∗=2,5时,在低约化速度下(2 .0 ≤Ur≤6.5),柱体处于涡激振动的初始分支和上端分支,此时柱体振动的平衡位置并未出现较大的偏移;随着约化速度的增大,柱体进入到涡激振动-驰振共同作用的区间,振动的平衡位置逐渐偏离了原来静止时的位置,向一侧偏移.其中质量比m∗=2 的柱体,柱体振动的偏移量最大.当柱体的质量为m∗=7,10 时,平衡位置偏移量(|y0|/D)随着约化速度的增加而不断偏离静止时的位置,虽然质量比较大,但是柱体偏移量的增长幅度较小.这是由于D 形截面柱体在横流向上不对称,升力总是更倾向于指向截面的直边一侧,升力的时间平均值不在零线附近.
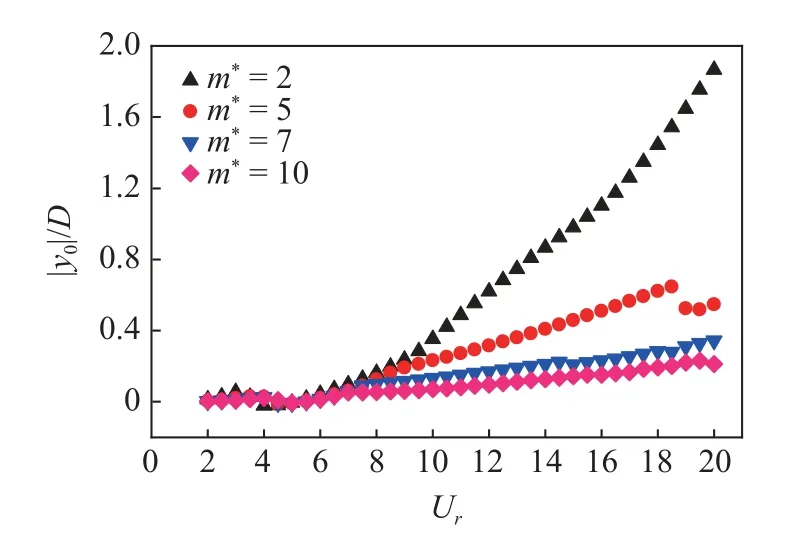
图5 振动平衡位置偏移量随约化速度的变化Fig.5 Variation of equilibrium position offset with reduced velocity
图6 为不同质量比下的横流向D 形截面柱体的最大振幅ymax随约化速度的变化情况.从图6 中可知,质量比对柱体振动特性具有显著的影响.以质量比m∗=10 为例,当质量比m∗=10 时,可以看到D 形截面柱体振幅响应的四个分支:初始分支(2 ≤Ur≤3)、上端分支(3 ≤Ur≤4.5)、涡激振动-驰振分支(5 .0 ≤Ur≤13.5)以及驰振分支(13.5 ≤Ur≤20).其中柱体的初始、上端分支所在的区间都很窄,柱体在上端分支的最大无量纲振幅只有0.2De,在离开上端分支后,柱体进入了涡激振动-驰振分支,D 形截面柱体与圆柱体的振动特性[28]不同,振幅没有出现振幅骤降的现象,而是表现为逐渐下降.在Ur=13.5之后,结合柱体振动的频率图(图7),柱体振动的频率很小(fs/fn,water=0.67),但振幅不断增大,呈现出高振幅、低频率特征,此时柱体进入到驰振分支.当柱体的质量比m∗=7 时,柱体在Ur=15.0 之后才进入到驰振分支中;当m∗=5 时,柱体在更大约化速度时才进入到驰振分支.在本次模拟中,当m∗=2 时没有捕捉到驰振分支,且振幅最小;质量比m∗=5 时,柱体振幅出现最大值.从对比来看,在相同的响应分支区间里,质量比越小,振幅往往越大.
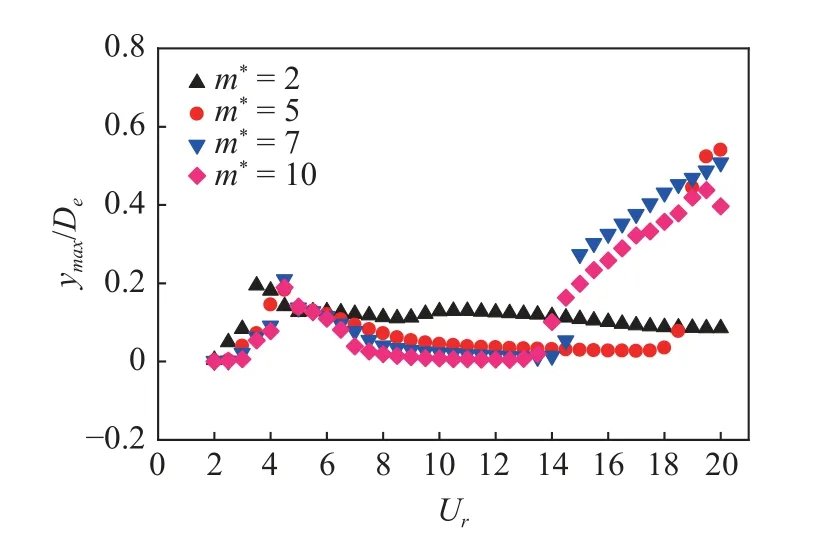
图6 最大振幅随约化速度的变化Fig.6 Variation of maximum amplitude with reduced velocity
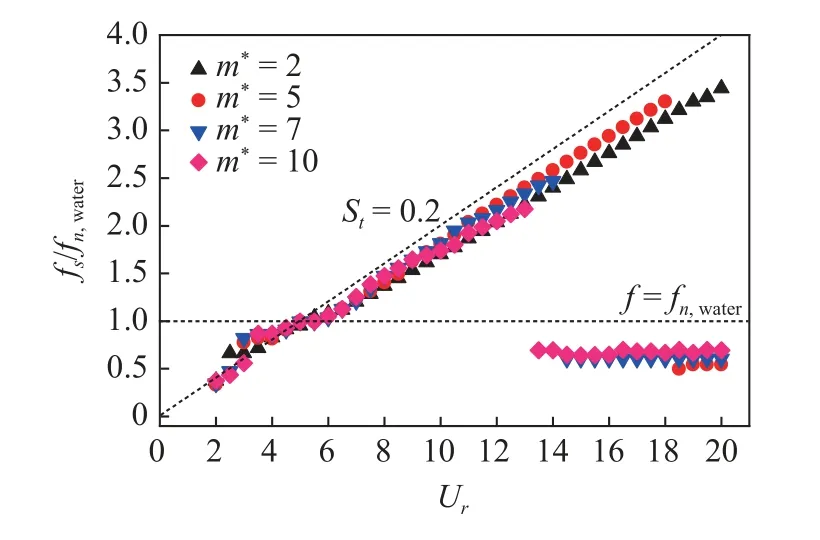
图7 主导振动频率随约化速度的变化Fig.7 Variation of dominant frequency with reduced velocity
3.2 振动频率
图7 展示了不同质量比下D 形截面柱体的无量纲振动频率(fs/fn,water)随着约化速度的变化趋势,其中fs为柱体的振动频率,可通过柱体位移时程曲线进行快速傅里叶变换(FFT)并提取主导频率后得到.图8 为D 形截面柱体的在几个不同约化速度下振动的频率谱.
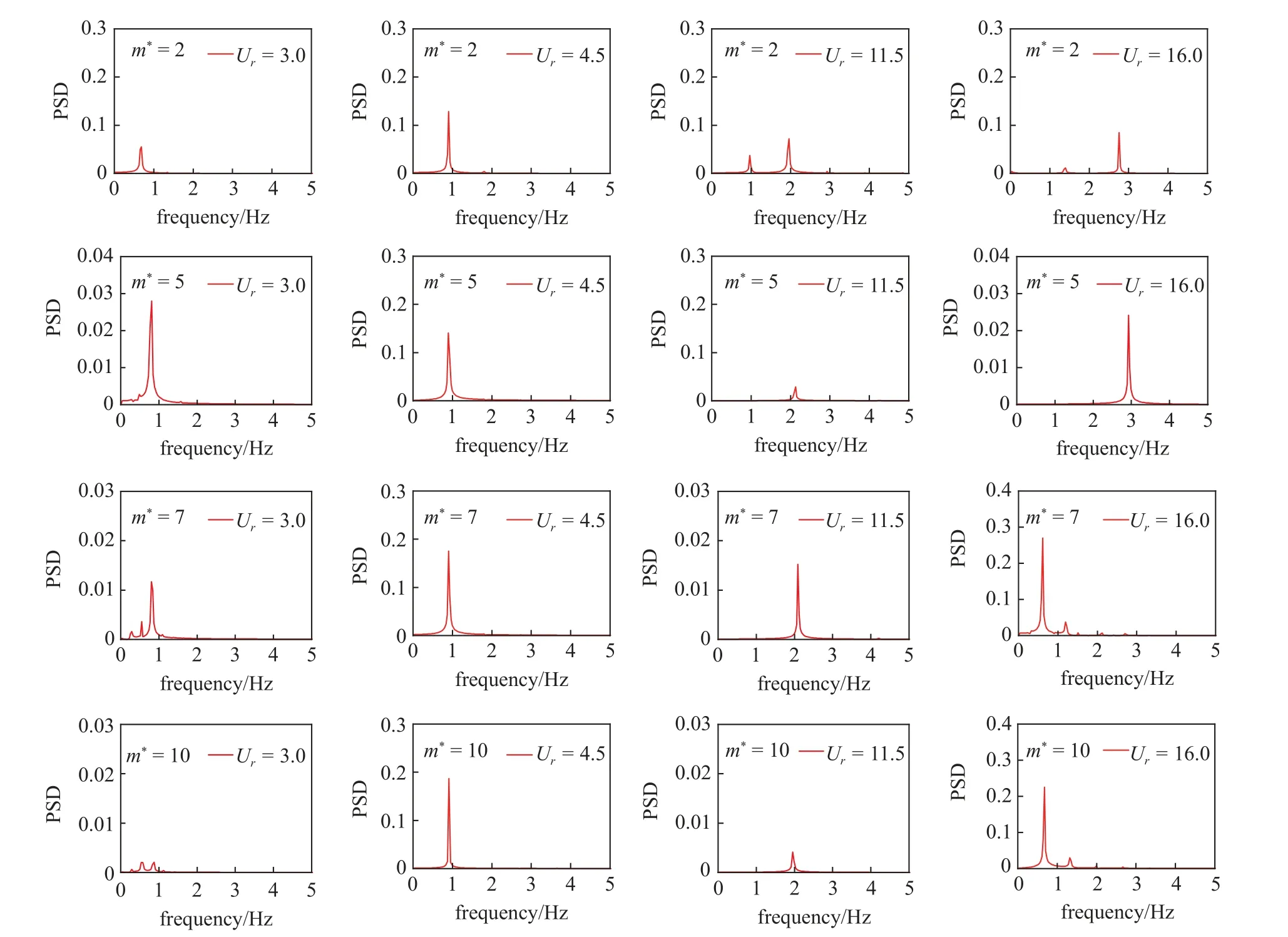
图8 D 形截面柱体振动的频率谱Fig.8 Vibration frequency spectra of D-section prism
从图8 可以看到,在低约化速度下,随着质量比的增大,柱体的无量纲振动频率随着约化速度的增加而不断增大.当柱体的质量比m∗=2 时,在约化速度 2 .0 ≤Ur≤4.0 时,柱体处于涡激振动的初始分支和上端分支,柱体的振动频率是单倍频且在St=0.2附近,此时柱体的振幅和平衡位置偏移量都很小.在约化速度Ur≥6.5 时,柱体的振动频率是双倍频且在St=0.2 的下方,并且靠近St,振幅很小,近似于涡激振动.但并不能说明此时柱体发生了涡激振动,此时柱体的振幅是不断变化的,实际上此时的柱体处于涡激振动-驰振共同作用的分支.
当柱体的质量比m∗=10 时,柱体在低约化速度下,进入涡激振动分支.在 2 .0 ≤Ur≤3.0 区间中,柱体处于涡激振动的初始分支,柱体的振动频率落在了St上,此时柱体的振幅很小.在 3 .5 ≤Ur≤6.0 时,柱体进入到了上端分支,振动的频率比在1.0 附近,结合前文的振幅响应图可以发现,此时柱体有最大的振幅.此后柱体进入到涡激振动-驰振共同作用的分支,在这个分支中,涡激振动占主导作用,表现为图8 (m∗=10,Ur=11.5)中只有一个主频.在高约化速度下(Ur≥13.5)进入到驰振分支,此时柱体的无量纲振动频率均小于1,且柱体的振幅不断增大,表明柱体进入到了驰振分支.
在同一个质量比的情况下,随着约化速度的增大,D 形截面柱体经历了涡激振动初始分支、上端分支、涡激振动-驰振分支以及驰振分支;柱体的振动频率逐渐由单倍频向多倍频转变;驰振在流致振动中的影响逐渐增大.对比来看,质量比对D 形截面柱体的振动响应有较大影响,质量越大的柱体其涡激振动的初始分支与上端分支的区间越大,柱体越容易进入到驰振分支,但振幅及平衡位置偏移量越小.
3.3 尾涡脱落模式
D 形截面柱体与圆柱相比,柱体的物理几何尖角对柱体后方尾迹区域的旋涡形成、脱落密切相关.柱体的振动振幅及频率是由柱体振动时所受到的流体力决定的,同时柱体表面的流动分离剪切层直接影响流体力,柱体后方旋涡的形成与脱落是这两者共同作用的结果.在本文研究的雷诺数范围内,根据柱体后方尾涡的形成与脱落过程,观察到多种不同的旋涡脱落形态,如“2S”(图9)、“4S+4S”(图10)等,其中“4S+4S”表示在一个振动周期内柱体两侧各脱落4 个旋涡[28].

图9 m*=2 柱体的尾涡脱落模式(Ur=13.0)Fig.9 Vortex shedding mode of the cylinder at m*=2 and Ur=13.0

图10 m*=10 柱体的尾涡脱落模式(Ur=16.0)Fig.10 Vortex shedding mode of a cylinder at m*=10 and U r=16.0
图9 和图10 分别给出了m*=2,10 的多个瞬时尾涡脱落的形态.当柱体质量比m∗=2,在约化速度Ur=2.0 时(雷诺数为288),D 形截面柱体后方没有发生明显的尾涡交替脱落,而在其他的约化速度下,尾涡脱落模式为“2S”模式,如图9 所示.流体流经柱体时,柱体表面形成上下两侧的分离剪切层,分离剪切层之间相互作用,直边一侧的边界层上形成的旋涡S1,由于柱体截面存在几何尖角,在流动的过程中被切断并脱落,旋涡S1 与S2 大小几乎相等、旋转方向相反,交替从柱体上脱落.当柱体质量比m∗=10,在约化速度Ur=2.0 时(雷诺数为288),柱体振幅很小,再结合图7 的振动频率可见,此时柱体类似于固定圆柱绕流;在约化速度 2 .5 ≤Ur≤5 时,柱体处于涡激振动的分支,尾涡脱落模式为“2S”;在约化速度 5 ≤Ur≤13 时,柱体处于涡激振动-驰振共同作用的区间,且涡激振动占主导;在约化速度13.5 ≤Ur≤20 时,柱体进入到驰振区间,无量纲振动频率降低至0.67 附近,尾涡脱落模式由“2S”模式转变成“4S+4S”,即在一个振动周期内从D 形截面柱体两侧各脱落4 个旋涡,如图10 所示.采用图9 和10 所示的方法,可以识别各个工况下的尾涡脱落模式,汇总结果见图11,其中红色叉号代表着此时柱体无尾涡脱落,“SS”表示柱体两侧后方同时脱落一个旋涡[32].从图11 可以看到,不同质量比柱体的尾涡脱落模式,在中低约化速度是比较接近的,多数情况是“2 S”模式,但是在高约化速度时,较高质量比的尾涡脱落模式出现了更多的变化,而低质量比m*=2时在本文计算范围内尾涡脱落形态都表现为“2S”模式.

图11 4 种质量比不同约化速度的尾涡脱落模式变化Fig.11 Variations of vortex shedding patterns with reduced velocity at four different mass ratios
3.4 一级能量转化效率
根据前文1.3 部分给出的方法和公式,计算了四个不同质量比下D 形截面柱体流致振动能量的一级转化效率,结果见图12.
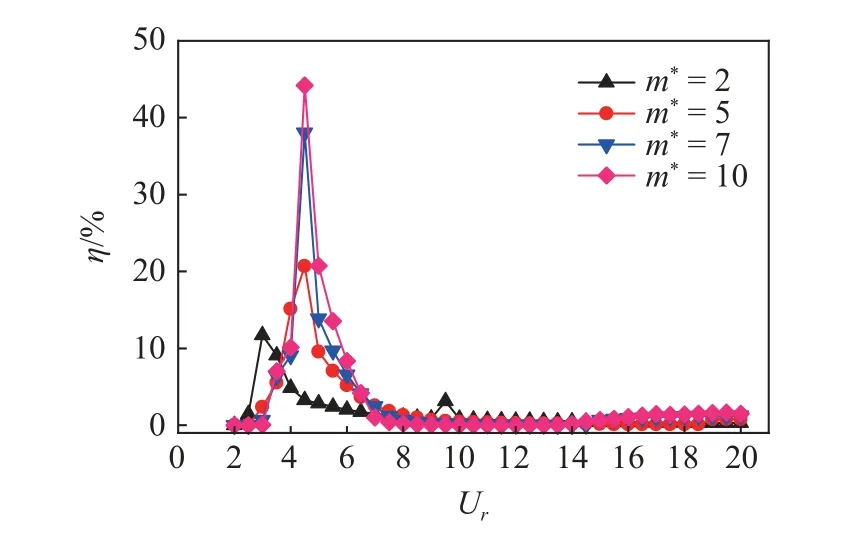
图12 能量转化效率的对比Fig.12 Comparison of the energy conversion efficiency
从图12 可以发现,在约化速度较低时,由于柱体的振幅、频率都较低,因此其俘能效率处于较低的水平;而当来流速度增大后,柱体的能量转化效率也随之同步增加,柱体的振动频率逐渐接近系统的固有频率,所处的区间为涡激振动的区间.随着约化速度持续增大,驰振对柱体的影响逐渐增强,柱体此时处于涡激振动-驰振的区间,柱体的振幅逐渐降低,能量转化效率也逐渐下降,当柱体进入到驰振区间后,柱体的能量转化效率也逐渐增大.出现这种变化的原因,可能是由涡激振动向驰振转化的过程中,柱体的振动频率降低导致转化效率下降,在进入到驰振区间后,D 形截面柱体的振幅发生了大幅增长,从而提高了能量转化效率,但由于柱体频率较低,柱体能量转化效率的提升并不显著.
通过图12 的对比来看,质量比对D 形截面柱体的能量转化效率的影响较为明显.另外,结合前文3.1 部分关于振动分支的划分,当柱体处于涡激振动的分支时,其能量转化效率最大.在本文研究范围内,质量比m∗=10 且Ur=4.5 时,D 形截面柱体一级能量转化效率达到最大值44%.
4 结论
本文对4 种不同质量比D 形截面柱体的流致振动进行了数值模拟,处于亚雷诺数区间(288 ≤Re≤2880),分别对不同约化速度下的D 形截面柱体的振幅、频率、平衡位置偏移量、尾涡脱落形态及能量转化效率等进行了对比分析.本文得到以下结论.
(1)在模拟计算的范围内,质量比越大的柱体,进入驰振区间对应的约化速度越低.随着约化速度的变化,D 形截面柱体在低约化速度下均观察到典型的涡激振动分支,包括涡激振动的初始分支、上端分支.质量比为2 时,随约化速度增大离开上端分支进入涡激振动-驰振分支,未发现明显的驰振分支;质量比为5,7 和10 时,柱体离开涡激振动-驰振分支后,进入驰振区间时的约化速度依次减小.
(2)柱体的质量比对柱体平衡位置偏移量有较大的影响.在本文考虑的范围中,质量比越大的柱体,流致振动的平衡位置偏移量越小.
(3)在涡激振动区间,柱体的尾涡脱落模式多数为“2S”,在驰振区间,尾涡脱落转为“nS+mS”模式.在本文模拟的工况中,柱体质量越大,尾涡处于“2S”模式的约化速度区间越窄.
(4)约化速度显著影响柱体的一级能量转换效率.高能量转化效率出现在涡激振动分支,而不是在驰振分支.质量比对一级能量转化效率影响在约化速度2~8 区域较明显,而在其他约化速度区域的差异较小.
限于篇幅,本文只关注于一个迎流角.至于不同迎流角、不同质量阻尼比的影响以及其他雷诺数范围的情况,还有待进一步的研究.
致谢
感谢国家超级计算天津中心、天津城建大学高性能计算平台对本文数值计算工作给予的支持.
